Оценка эффективности реальных инвестиций
 Скачать 347.85 Kb. Скачать 347.85 Kb.
|
|
Министерство образования и науки РФ Казанский государственный архитектурно-строительный университет Кафедра Экономики и предпринимательства в строительстве Курсовая работа на тему: «Оценка эффективности реальных инвестиций» по дисциплине: экономическая оценка инвестиций Выполнил: студент гр. 0ЭС-403 Щербакова В.М. Проверил: Боровских О. Н. Казань 2013 Раздел I Глава 1. Моделирование оценки стоимости финансовых инструментов инвестирования В процессе выбора финансовых инструментов инвестирования каждый инвестор ставит перед собой две основные задачи – максимизировать доход и минимизировать риск обращения. В связи с противоречивым характером этих задач процесс обоснования носит оптимизационный характер. Средством такой оптимизации выступают разнообразные модели оценки стоимости финансовых инструментов инвестирования, в основе которых лежит выявление оптимальной шкалы соотношений уровней доходности и риска, удовлетворяющих любого инвестора. Современная теория выделяет следующие основные модели оценки стоимости финансовых инструментов инвестирования:
Задача №1 Необходимо рассчитать: -стоимость простой акции при ее использовании в течение неопределенного продолжительного периода времени; -текущую рыночную стоимость акции при ее использовании в течение заранее определенного срока; - текущую рыночную стоимость акции с постоянными дивидендами; -текущую рыночную стоимость акции с постоянно возрастающими дивидендами (по модели Гордона); -стоимость акции с колеблющимся уровнем дивидендов по отдельным периодам; -стоимость облигаций с периодической выплатой процентов; -стоимость облигаций с выплатой всей суммы процентов при ее погашении; -стоимость облигаций, реализуемой с дисконтом без выплаты процентов; -дивидендную и текущую нормы доходности акции и текущий уровень доходности облигаций; -сделать выводы о выборе наиболее предпочтительной модели. Таблица 1 Исходные данные для расчета рыночной стоимости акций и облигаций:
1.1. Основные модели, используемые при формировании текущей рыночной цены акции 1) Модель оценки стоимости простой акции при ее использовании в течение неопределенного продолжительного периода времени: 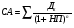 (1) (1)СА - реальная стоимость акции, используемый неопределенное число лет; Дt - сумма дивидендов, предполагаемая к получению в каждом периоде; НП - ожидаемая доходность по акциям; t - число периодов, включенных в расчет. 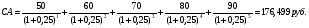 Экономическое содержание данной модели заключается в том, что текущая рыночная стоимость акции представляет собой сумму дивидендов по отдельным периодам, приведенную к настоящей стоимости по дисконтной ставке, равной норме текущей доходности по ней. 2) Модель оценки текущей рыночной стоимости акций при их использовании в течение заранее определенного срока: CA= 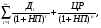 (2) (2)ЦР – прогнозируемая рыночная цена реализации акции в конце периода ее использования. 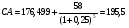 руб. руб.3) Модель оценки текущей рыночной стоимости акций с постоянными дивидендами: 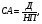 (3) (3)Д – годовая сумма постоянного дивиденда. 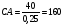 руб руб4) Модель оценки текущей рыночной стоимости акций с постоянно возрастающими дивидендами (модель Гордона): СА= 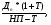 (4) (4)Д - сумма последнего уплаченного дивиденда; Т – темп прироста дивидендов, выраженный десятичной дробью. СА= 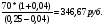 5) Модель оценки стоимости акций с колеблющимся уровнем дивидендов по отдельным периодам: СА= 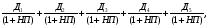 (5) (5)Д1… Дn – сумма дивидендов, прогнозируемых к получению в каждом периоде. CA= 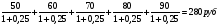 Указанные модели оценки реальной рыночной стоимости акций используются для их отбора и включения в инвестиционный портфель. 1.2. Основные модели, используемые при формировании текущей рыночной цены облигации 1) Базисная модель оценки стоимости облигаций или облигаций с периодической выплатой процентов: CO= 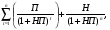 (6) (6)СО – стоимость облигаций; П - сумма процента, выплачиваемая в каждом периоде (представляющая собой произведение ее номинала на объявленную ставку процента); Н - номинал облигации, подлежащий погашению в конце срока ее обращения. 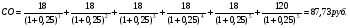 2) Модель оценки стоимости облигации с выплатой всей суммы процентов при ее погашении: 2) Модель оценки стоимости облигации с выплатой всей суммы процентов при ее погашении:CO= 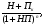 (7) (7)Пk - сумма процентов по облигации, подлежащая выплате в конце срока ее обращения. CO= 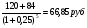 Модель оценки стоимости облигации, реализуемой с дисконтом без выплаты процентов: CO= 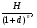 (8) (8)d- дисконт. CO= 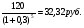 Трансформируя указанные модели можно рассчитать ожидаемую доходность. Доходность акций и облигаций вычисляется в следующем порядке. Дивидендная норма доходности акции: Днд= 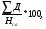 (9) (9)∑Д – сумма дивидендов по акции; Нса - номинальная стоимость акции. Днд = 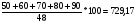 Текущая норма доходности акции: Тнд = 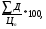 (10) (10) Ц- цена приобретения акции. Тнд= 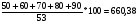 Для оценки текущего уровня доходности облигации используется коэффициент ее текущей доходности: Ктдо = 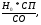 (11) (11) Н0- номинал облигации; СП – объявленная ставка процента (купонная ставка); СО – реальная текущая стоимость облигации (или текущая ее цена). Ктдо= 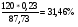 Ктдо= 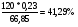 Ктдо= 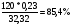 Вывод: самым выгодным методом, используемым при определении текущей рыночной цены облигации, является модель оценки стоимости облигации реализуемой с дисконтом без выплаты процентов, так как в этом случае цена облигации наибольшая. Глава 2. Моделирование рациональной структуры инвестиционного портфеля Современное финансовое инвестирование непосредственно связано с формированием инвестиционного портфеля. Оно базируется на том, что большинство инвесторов избирают для финансового инвестирования более чем один финансовый инструмент, то есть формируют их совокупность. Инвестиционный портфель представляет собой целенаправленно сформированную совокупность объектов реального и финансового инвестирования, предназначенных для осуществления инвестиционной деятельности в соответствии с разработанной инвестиционной стратегией предприятия. Ключевой целью управления инвестиционным портфелем является обеспечение наиболее эффективных путей реализации инвестиционной стратегии предприятия на фондовом рынке. Причем цели эмитентов и инвесторов на данном рынке не совпадают. Инвестиционная стратегия предприятия – эмитента заключается в наиболее быстром и выгодном для себя размещении эмиссионных ценных бумаг среди потенциальных инвесторов для привлечения дополнительного капитала. Инвестиционная стратегия предприятия, выступающего в роли инвестора, многопланова и преследует различные цели: непосредственное управление объектом инвестирования, формирование фондового портфеля с целью получения доходов в результате повышения курсовой стоимости ценных бумаг и др. У. Шарп предлагает следующую последовательность действий по формированию и оперативному управлению инвестиционным портфелем:
Возможно уточнить и дополнить эти этапы инвестиционного процесса следующими положениями: Исследование внешней инвестиционной среды и прогнозирование конъюнктуры на финансовом рынке: правовые условия инвестиционной деятельности, анализ текущего состояния, прогнозирование конъюнктуры рынка в разрезе его сегментов и в целом; Разработка стратегических направлений инвестиционной деятельности предприятия; Разработка стратегии формирования инвестиционных ресурсов для реализации выбранной инвестиционной стратегии, к таким ресурсам относятся как собственные, так и привлеченные с финансового рынка средства; Поиск и оценка инвестиционной привлекательности отдельных видов ценных бумаг для включения их в портфель; Формирование инвестиционного портфеля и его оценка по критериям доходности, безопасности и ликвидности. Расчет ведется по каждому фондовому инструменту. Ожидаемая доходность портфеля d рассчитывается как средневзвешенная величина ожидаемых доходностей входящих в него различных активов: При покупке какого-либо актива инвестор учитывает не только значение его ожидаемой доходности, но и уровень его риска. Ожидаемая доходность выступает как средняя ее величина в соответствии с имевшей место динамикой актива на фондовом рынке. Фактическая доходность, как правило, будет отличной от расчетной ожидаемой. То есть всегда имеется степень риска получить доходность ниже ожидаемой. В практике управления портфелями ценных бумаг в качестве способа расчета величины риска используют показатели дисперсии и стандартного отклонения показателя фактической доходности от величины расчетной ожидаемой. Знание ожидаемой доходности активов, а также уровня риска ее получения используются при формировании инвесторами так называемых оптимальных портфелей ценных бумаг. Оптимизация портфеля ценных бумаг состоит в определении пропорций в составе входящих в него активов, которые обеспечили бы максимальную доходность при минимуме риска. При этом следует отметить, что, как правило, чем выше предполагаемая доходность актива, тем выше и степень риска ее получения. И наоборот, активы, имеют гораздо меньшую доходность. Принцип нахождения оптимального портфеля ценных бумаг состоит в рассмотрении вариаций его состава с различными пропорциями состава активов и в расчете для каждого варианта среднего уровня доходности и показателя ковариации. В соответствии с данными показателями инвестор или его доверенное лицо, управляющее портфелем, принимают соответствующие решения по изменению состава портфеля. Задача №2. На основание данных состояния фондового рынка и динамики изменения стоимости обращающихся на нем различных ценных бумаг в предшествующие годы сделаны следующие расчеты показателей, отражающие параметры возможных вложений денежных средств. Требуется дать заключение по этим расчетам и определить наиболее предпочтительный вариант портфеля. Необходимо определить: -ожидаемую доходность портфелей по периодам; -среднее значение доходности активов; -стандартное отклонение доходности по отдельным финансовым активам и портфелям; -показатель ковариации портфелей; -коэффициент корреляции портфелей; -риск портфелей; -сделать соответствующие выводы о выборе предпочтительного портфеля. Таблица 2 Параметры вариантов портфелей ценных бумаг
Средняя доходность определяется как средняя арифметическая доходность актива за периоды наблюдения: ri– доходность актива в i- м периоде; n – число периодов наблюдения. по активу А: r= (2+2,4+3,8+3,4) /4=2,9 по активу Б: r= (2,2+3,6+2,6+3,2)/4=2,9 по активу В: r=(3,8+2,8+3+3,6)/4=3,3 по 1 портфелю: r=(2,160+3,360+2,840+3,240)/4=2,9 по 2 портфелю: r=(3,480+2,960+2,920+3,520)/4=3,22 по 3 портфелю: r=(3,440+2,720+3,160+3,560)/4=3,22 Стандартное отклонение доходности активов σ определяется: σ = Величина дисперсии рассчитывается по формуле:  (15) (15) 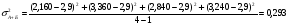 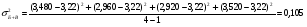 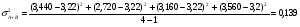 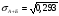 =0,54 =0,54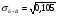 =0,32 =0,32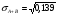 =0,37 =0,37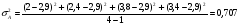 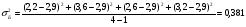 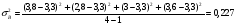 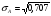 =0,84 =0,84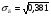 =0,62 =0,62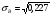 =0,48 =0,48Вывод:наибольшая величина стандартного отклонения наблюдается у актива А, следовательно данный актив обладает наибольшим риском. Риск портфеля показывает количественное измерение рискованности портфеля. Показатель ковариации определяется по формуле: r Аi , rБi – доходность активов А и Б в i – м периоде; rА ,rБ - средняя доходность активов А и Б. СА-Б=((2-2,9)*(2,2-2,9)+(2,4-2,9)*(3,6-2,9)+(3,8-2,9)*(2,6-2,9)+(3,4-2,9)*(3,2-2,9))/3=0,053 Значение ковариации положительное, и это говорит о том ,что доходность активов А-Б изменяется в одном направлении. СБ-В=((2,2-2,9)*(3,8-3,3)+(3,6-2,9)*(2,8-3,3)+(2,6-2,9)*(3-3,3)+(3,2-2,9)*(3,6-3,3))/3=-0,173 - разные направления активов СА-В=((2-2,9)*(3,8-3,3)+(2,4-2,9)*(2,8-3,3)+(3,8-2,9)*(3-3,3)+(3,4-2,9)*(3,6-3,3))/3=- 0,107 - разные направления активов Другим применяемым показателем степени взаимосвязи, где изменения доходностей двух активов является коэффициент корреляции RА-Б, рассчитывается по формуле: СА-Б- ковариация доходности активов А и Б; RА-Б=0,053/(0,84*0,62)=0,102 – доходность меняется в одном направлении. RБ-В= -0,173/(0,62*0,48)= -0,585 - в противоположных направлениях RА-В=-0,107/(0,84*0,48)= -0,267 - в противоположных направлениях Риск (дисперсия) портфеля, состоящего из нескольких активов, рассчитывается по формуле: Сi-j - ковариация доходности активов, входящих в портфель; y i ,yj - удельные веса активов в общей стоимости портфеля. Риск портфеля σ2p , состоящего из двух активов рассчитывается по формуле: yА ,yБ - удельные веса активов А и Б в портфеле ценных бумаг; СА-Б - ковариация доходности активов А и Б; σ2А-Б = 0,22*0,842+0,82*0,622+2*0,2*0,8*(0,053)=0,293 σ2Б-В = 0,22*0,622+0,82*0,482+2*0,2*0,8*(-0,173)=0,105 σ2А-В = 0,22*0,842+0,82*0,482+2*0,2*0,8*(-0,107)=0,162 Вывод: наиболее высоко доходным будет актив В, у которого наибольшее среднее значение доходности равное 3,3 . Стандартное отклонение показывает, насколько варьируется значение доходности активов от средней величины и увеличение этого показателя будет сигнализировать о повышение уровня риска. Наименьшее значение стандартного отклонения у портфеля Б-В равное 0,32. Следовательно, наименее рискованным будет портфель Б-В, у которого наименьшее значение ковариации, равное -0,173. Глава 3. Определение доходности инвестиционного портфеля На практике существует прямая зависимость между доходностью и уровнем риска эмиссионных ценных бумаг. Выделяют следующие виды доходов по ценным бумагам: - дивиденды и проценты в форме текущих выплат; - доходы от увеличения курсовой стоимости финансовых инструментов, находящихся в портфеле (реализуются при их перепродаже на рынке в виде разницы между ценой покупки и ценой продажи); - премии и разницы при вложении денежных средств в производные фондовые инструменты (опционы и фьючерсы); - комиссионное вознаграждение, возникающее при управлении портфельными инвестициями в порядке доверительного управления и др. Инвестиционный портфель имеет ограничение по сроку жизни, а также по минимальной и максимальной сумме инвестиций. Для измерения совокупности доходности портфеля в годовом исчислении рекомендуется использовать следующую формулу:  , (21) , (21)ДИП - доходность инвестиционного портфеля, %; ПДП - полученные дивиденды и проценты, руб.; РКП - реализованная курсовая прибыль, руб.; НКП - нереализованная курсовая прибыль, руб.; НИ - начальные инвестиции, руб.; ИС- извлеченные средства из инвестиционного портфеля, руб.; ДС - дополнительные средства, вложенные в портфель, руб.; Данная формула включает как реализованные (текущие поступления плюс прирост курсовой стоимости ценных бумаг), так и нереализованные доходы в результате прироста курсовой стоимости за год. Значения показателя доходности инвестиционного портфеля, полученное в результате финансовых вычислений, можно использовать для анализа его прибыльности, скорректированной с учетом параметров фондового рынка. Такой сравнительный анализ удобен для инвестора, поскольку позволяет установить, насколько положительным является конкретный портфель относительно рынка ценных бумаг в целом. Задача № 3 Произвести расчет доходности инвестиционного портфеля. Таблица 3 Данные для определения доходности инвестиционного портфеля
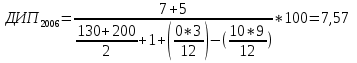 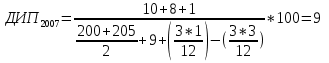 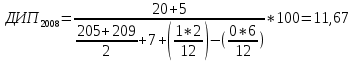 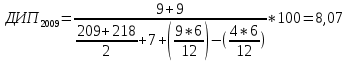 Вывод: В 2008 году доходность инвестиционного портфеля является самой высокой, потому что в этом году полученные дивиденды и проценты максимальны, есть реализованная курсовая прибыль. Самая низкая доходность инвестиционного портфеля в 2006 году, так как здесь отсутствуют полученные дивиденды и проценты, а также достаточно много средств и извлечено из портфеля. Задача. Для расширения складских помещений предприятия планируют через период времени Т2приобрести здание. Эксперты оценивают будущую стоимость недвижимости в размере Н. По банковским депозитам установлены процентные ставки с ежегодной схемой начисления процентов d. Определить, какую сумму средств необходимо поместить на банковский счет, чтобы получить достаточную сумму средств для покупки недвижимости. Исходные данные: Таблица 4
Решение: Решаем задачу с помощью формулы дисконтирования по сложным процентам: PV= 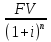 , ,где: PV – текущая стоимость денег (руб.); FV – будущая стоимость денег (руб.); i – процентная ставка за период (%); n – число периодов начисления процентов. PV= 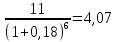 тыс. руб. тыс. руб.Ответ: на банковский счет необходимо поместить сумму средств в размере 4,07 тыс. руб., чтобы получить достаточную сумму средств для покупки недвижимости. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
