математические методы в психологии. мат.методы в психологии Ушакова А.И.. Федеральное государственное бюджетное образовательное учреждение высшего образования башкирский государственный педагогический университет им. М. Акмуллы
 Скачать 414.5 Kb. Скачать 414.5 Kb.
|
|
Основными задачами факторного анализа являются следующие: · отбор факторов, которые определяют исследуемые результативные показатели; · классификация и систематизация факторов с целью обеспечения возможностей системного подхода; · определение формы зависимости между факторами и: результативным показателем; · моделирование взаимосвязей между результативными и факторными показателями; · расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя; · работа с факторной моделью, т.е. практическое ее использование для управления экономическими процессами. Отбор факторов для анализа того или другого показателя осуществляется на основе теоретических и практических знаний, приобретенных в этой отрасли. При этом обычно исходят из принципа: чем больше комплекс факторов исследуется, тем точнее будут результаты анализа. Вместе с тем необходимо иметь в виду, что если этот комплекс факторов рассматривается как механическая сумма, без учета их взаимодействия, без выделения главных, определяющих, то выводы могут быть ошибочными. В экономическом анализе взаимосвязанное исследование влияния факторов на величину результативных показателей достигается с помощью их систематизации. Фактор называется генеральным, если все его нагрузки значительно отличаются от нуля, т.е. он имеет нагрузки от всех переменных. Фактор называется общим, если хотя бы две его нагрузки значительно отличаются от нуля (т.е. он имеет нагрузки от двух и более переменных). Число высоких нагрузок переменной на общие факторы называется ее сложностью. Одной из особенностей факторного анализа является понятие компонентов дисперсии. Общностьпараметра zj, связанная с общими факторами, представляет собой часть единичной дисперсии переменной, которую можно приписать общим факторам. Она равна квадрату коэффициента множественной корреляции между переменной и общими факторами, т.е. сумме квадратов факторных нагрузок: (j = 1, 2, ..., n). По сути дела, общности представляют собой диагональные элементы матрицы корреляций между исследуемыми переменными. Характерностьпредставляет собой часть единичной дисперсии переменной, которая не связана с общими факторами, т. е. вклад характерного фактора Uji. Характерность показывает, насколько в общих факторах учтена суммарная дисперсия параметра. Характерность можно разбить на две составляющие – специфичность и дисперсию, обусловленную ошибкой. Специфичность– доля характерности, которая тем или иным образом связана с действительной спецификой изучаемого параметра. Дисперсия ошибки (ненадежность) параметра связана с несовершенством измерений. Надежностьесть разница между полной дисперсией и дисперсией ошибки, т.е. представляет собой сумму общности и специфичности. Значение надежности является верхней границей общности. Разница между надежностью и общностью является мерой специфической дисперсии, присущей только одной определенной переменной. Переменные, характеризующиеся малой надежностью, в факторный анализ включаться не должны. 33.Многомерное шкалирование. Сущность, этапы проведения. Примеры применения в психологических исследованиях. Задача многомерного шкалирования в самом общем виде состоит в том, чтобы выявить структуру исследуемого множества стимулов. Под выявлением структуры понимается выделение набора основных факторов, по которым различаются стимулы, и описание каждого из стимулов в терминах этих факторов. Процедура построения структуры опирается на анализ объективной или субъективной информации о близостях между стимулами либо информации о предпочтениях на множестве стимулов. В случае анализа субъективных данных решаются одновременно две задачи. С одной стороны, выявляется объективная структура субъективных данных, с другой — определяются факторы, влияющие на процесс принятия решения. Методы многомерного шкалирования могут использовать разные типы данных: данные о предпочтениях субъекта на множестве стимулов, данные о доминировании, о близостях между стимулами, данные о профилях и т. п. Как правило, с каждым типом данных принято соотносить определенную группу методов их обработки. Однако такое соотнесение не должно быть слишком жестким, поскольку часто не представляет особого труда перейти от одного типа данных к другому. Так, например, данные о профилях можно легко преобразовать в данные о близостях, для этого необходимо только воспользоваться подходящей метрикой. Данные о предпочтениях содержат в себе информацию о доминировании. С другой стороны, подсчитав корреляции между столбцами матрицы предпочтений, получим матрицу близостей между стимулами, а корреляции между строками той же матрицы дадут нам матрицу близостей между субъектами. В настоящей работе будет обсуждаться только анализ близостей. В основе многомерного шкалирования лежит идея геометрического представления стимульного множества. Предположим, что нам задано координатное пространство, каждая ось которого соответствует одному из искомых факторов. Каждый стимул представляется точкой в этом пространстве, величины проекций этих точек на оси соответствуют значениям или степеням факторов, характеризующих данный стимул. Чем больше величина проекций, тем большим значением фактора обладает стимул. Мера сходства между двумя стимулами обратна расстоянию между соответствующими им точками. Чем ближе стимулы друг к другу, тем выше мера сходства между ними (и ниже мера различия), далеким точкам соответствует низкая мера сходства. Чтобы точным образом измерить близости, необходимо ввести метрику в искомом координатном пространстве; выбор этой метрики оказывает большое влияние на результат решения. Обычно используется метрика Минковского:  где r — размерность пространства, djk — расстояние между точками, соответствующими j-му и k-му стимулам, Xjt, Xkt — величины проекций j-й и k-й точек на t-ю ось. Наиболее распространенными ее случаями являются: евклидова метрика (р=2): 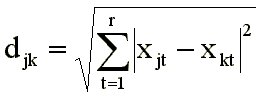 и метрика «city-block» (р=1) 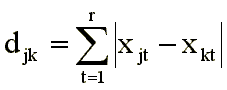 В некоторых случаях пользуются метрикой доминирования (р стремится к бесконечности):  Использование равномерных метрик предполагает, что при оценке сходств (различий) субъект в одинаковой мере учитывает все факторы. Когда же имеется основание утверждать, что факторы неравноценны для индивида и он учитывает их в разной степени, прибегают к взвешенной метрике, где каждому фактору приписывается определенный вес. Разные индивиды могут принимать во внимание разные факторы. Тогда каждый индивид характеризуется своим собственным набором весов Wti. Взвешенная метрика Минковского имеет вид: 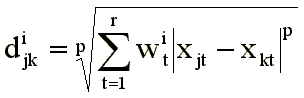 Такая модель называется «индивидуальным шкалированием» или «моделью взвешенных факторов» [2, 12, 13]. Геометрически она интерпретируется следующим образом. Пусть в координатном пространстве имеется конфигурация точек, отражающая восприятие некоторого «среднего индивида» в группе. Для того чтобы получить пространство восприятия i-го субъекта, необходимо растянуть «среднюю конфигурацию» в направлении тех осей, для которых Wti > Wtср, и сжать в направлении осей, для которых Wti < Wtср. Например, если в пространстве двух факторов для «среднего индивида» все стимулы лежат на окружности, то для индивида, характеризующегося весами W1i=2, W2i=1, эти стимулы будут располагаться на эллипсе, вытянутом вдоль горизонтальной оси, а для индивида, характеризующегося весами W2i=2, W1i=1, на эллипсе, вытянутом вдоль вертикальной оси. Схема многомерного шкалирования включает ряд последовательных этапов. На первом этапе необходимо получить экспериментальным способом субъективные оценки различий. Процедура опроса и вид оценок должны выбираться исследователем в зависимости от конкретной ситуации. В результате такого опроса должна быть сконструирована субъективная матрица попарных различий между стимулами, которая будет служить входной информацией для следующего этапа. На втором этапе решается задача построения координатного пространства и размещения в нем точек-стимулов таким образом, чтобы расстояния между ними, определяемые по введенной метрике, наилучшим образом соответствовали исходным различиям между стимулами. Для решения этой формальной задачи не требуется никаких сведений о самих стимулах, достаточно располагать только матрицей попарных различий между ними. Для построения искомого координатного пространства используется достаточно разработанный аппарат линейной или нелинейной оптимизации. Вводится критерий качества отображения, называемый «стрессом» и измеряющий степень расхождення между исходными различиями Djk и результирующими расстояниями djk. Ищется такая конфигурация точек, которая давала бы минимальное значение этому «стрессу». Значения координат этих точек и являются решением задачи. Используя эти координаты, мы строим геометрическое представление стимулов в пространстве невысокого числа измерений. Оно должно быть в достаточной степени адекватно исходным данным. Стимулы, которым в исходной матрице соответствуют большие меры различий, должны находиться далеко друг от друга, а стимулы, которым соответствуют малые меры различий, — близко. Формальным критерием адекватности может служить коэффициент корреляции, он должен быть достаточно высоким. Средство повышения точности формального решения состоит в увеличении числа измерений, т. е. размерности пространства r. Чем выше размерность пространства, тем больше возможностей получить более точное решение. Геометрическое представление стимулов в пространстве невысокого числа измерений является результатом, имеющим самостоятельное значение. Оно даст возможность наглядного представления данных, удобного для визуального анализа, и направления его использования далеко выходят за рамки психометрических исследований. На третьем этапе решается содержательная задача интерпретации формального результата, полученного на предыдущей стадии. Если на предыдущем этапе достаточно было только информации о попарных различиях между стимулами, то для содержательной интерпретации необходимо тщательное изучение их характеристик 34.Кластерный анализ. Сущность кластерного анализа, основные этапы его проведения. Примеры применения в психологических исследованиях. Кластерный анализ представляет собой класс методов, используемых для классификации объектов или событий в относительно однородные группы, которые наз. кластерами Кластерный анализ используется для: +сегментация рынка (например, потребителей можно разбить на кластеры на основе выгод, которые они ожидают получить от покупки данного товара) +понимание поведения покупателей -кластерный анализ используют для идентификации однородных групп покупателей. +определение возможностей нового товара - кластеризацией торговых марок и товаров можно определить конкурентоспособные наборы в пределах данного рынка. Торговые марки в одном и том же кластере конкурируют более жестко между собой, чем с марками других кластеров. Этапы выполнения кластерного анализа: 1. Формулировка проблемы (задача состоит в том, чтобы выбранный набор переменных смог описать сходство между объектами с точки зрения признаков, имеющих отношение к данной проблеме) 2. Выбор меры рассеяния (заключается в выборе способа измерения расстояния или меры сходства. Наиболее часто в качестве меры сходства используется расстояние между объектами. Объекты с меньшими расстояниями между собой более похожи, чем объекты с большими расстояниями. Существует несколько способов вычислить расстояние между объектами (Эвклидово расстояние; расстояние городских кварталов) 3. Выбор метода кластеризации (бывают иерархическими и неиерархическими) 4. Принятие решения о количестве кластеров 5. Интерпретация и профилирование кластеров 6. Оценка достоверности кластеризации Иерархические методы бывают агломеративная (объединяющая) кластеризация начинается с каждого объекта в отдельном кластере. Кластеры объединяют, группируя объекты каждый раз во всё более и более крупные кластеры. Этот процесс продолжается до тех пор, пока все объекты не станут членами одного кластера. дивизивная кластеризация начинается со всех объектов, сгруппированных в единственном кластере. Кластеры делят до тех пор, пока каждый объект не окажется в отдельном кластере. Обычно в МИ используются агломеративные методы, например, методы связи, дисперсионные и центроидные данные. Методы связи: - «метод ближайшего соседа» (одиночная связь) - первыми объединяют два объекта, расстояние между которыми минимально. Далее определяют следующее по величине самое короткое расстояние, и в кластер с двумя первыми объектами вводят третий объект. Расстояние между кластерами – расстояние между их ближайшими точками. - «далёкого соседа» (полная связь) – расстояния между кластерами вычисляют как расстояния между их самыми удалёнными точками. - «среднего расстояния» - расстояние между кластерами определяют как среднее значение всех расстояний между объектами двух кластеров. Неиерархические методы: Последовательный пороговый метод – выбирают центр кластера и все объекты, находящиеся в пределах заданного от центра порогового значения, группируют вместе. Затем выбирают новый кластерный центр, и процесс повторяют для несгруппированных точек. Параллельный пороговый метод работает аналогично, выбирают несколько кластерных центров и объекты в пределах порогового уровня группируют с ближайшим центром. Недостатки неиерархических методов: *число кластеров определяется заранее и выбор кластерных кластерных центров происходит независимо *многие неиерархические методы выбирают К-случаев (К-количество кластеров) и зависят от порядка наблюдений. 35.Оформление и представление результатов эмпирического исследования для печати в научных изданиях. Результаты законченной научной работы оформляются в виде отчета, статьи, доклада, диссертации и т. д., которые называют научными трудами. При подготовке научных трудов необходимо знание и соблюдение некоторых требований, предъявляемых к содержанию научной рукописи. Особенно важны ясность изложения, систематичность и последовательность в подаче материала. Текст рукописи следует делить на абзацы, т. е. на части, начинающиеся с красной строки. Правильная разбивка на абзацы облегчает чтение и усвоение содержания текста. Критерием такого деления является смысл написанного - каждый абзац включает самостоятельную мысль, содержащуюся в одном или нескольких предложениях. Не рекомендуется перегружать рукопись цифрами, цитатами, иллюстрациями, так как это отвлекает внимание читателя и затрудняет понимание содержания. Однако не следует, и отказываться совсем от такого материала, поскольку по нему читатели могут проверить результаты, полученные в исследовании. Весь вспомогательный материал лучше привести в отчете в виде приложения. Цитируемые в рукописи места должны иметь точные ссылки на источники. Необходимо соблюдать единство условных обозначений и допускаемых сокращений слов, которые должны соответствовать принятым стандартам. Основными составляющими научного труда являются следующие элементы. Название (заглавие) работы, которое должно быть кратким, определенным, отвечающим содержанию работы, так как по нему научная работа будет классифицирована в предметном каталоге. Название работы выносится на титульную страницу. Кроме того, на титульной странице указываются: - полное имя, отчество и фамилия автора (авторов) в именительном падеже; - должность, занимаемая автором (авторами) в момент написания работы; - название учреждения и города, где была выполнена работа; - год оформления; - фамилия, должность и ученое звание руководителя. Оглавление (содержание)работы предназначено для раскрытия в краткой форме содержания работы путем обозначения основных разделов, частей, глав и других подразделений рукописи. Содержание в рукописи помещается либо в начале ее, либо в конце. Иногда при оформлении научной работы возникает необходимость написать предисловие. В нем излагаются внешние предпосылки создания научного труда: - чем вызвано его появление; - когда и где была выполнена работа; - перечисляются организации и лица, оказывавшие содействие при выполнении данной работы. Введение,гдеавторы вводят читателя в круг проблем, дает постановку основного вопроса исследования, чтобы подготовить читателя к лучшему усвоению изложенного материала. В таком вступлении определяются: - значение проблемы, ее актуальность, цели и задачи, поставленные автором при написании научной работы; - состояние проблемы на данный момент времени. Не следует при этом затрагивать факты и выводы, излагаемые в последующих разделах научной работы. Вслед за вступлением дается краткий обзор литературы по рассматриваемому вопросу. Основная часть работы включаются материалы, методы, экспериментальные данные, обобщения и выводы самого исследования. При написании этого раздела необходимо представить себе вопросы по предлагаемому материалу, которые могут, прежде всего, заинтересовать читателя, и в соответствии с этим дать по ним исчерпывающий ответ. Цифровой материал, если он есть, представляется в форме, легко доступной обозрению (в виде таблиц, диаграмм, графиков) с соблюдением особой точности, так как неверные цифры могут привести к неверным выводам. Если же какой-то цифровой материал можно с достаточной ясностью и краткостью изложить в самом тексте, то его не следует облекать в табличную форму. В конце работы как итоговый материал пишутся выводы в виде кратко сформулированных и пронумерованных отдельных тезисов (положений). В заключении дается обобщение наиболее существенных положений научного исследования, подводятся его итоги, показывается справедливость выдвинутых автором новых положений, а также выдвигаются вопросы, которые еще требуют разрешения. |
