Вся навигация. вся навигация 1. Фигура и модели Земли

• Название: Фигура и модели Земли
• Анкор: Вся навигация
• Дата: 31.01.2023
• Размер: 3.45 Mb.
• Имя файла: вся навигация 1.doc
• Тип: Документы; #913997
• страница: 1 из 9

Фигура и модели Земли

С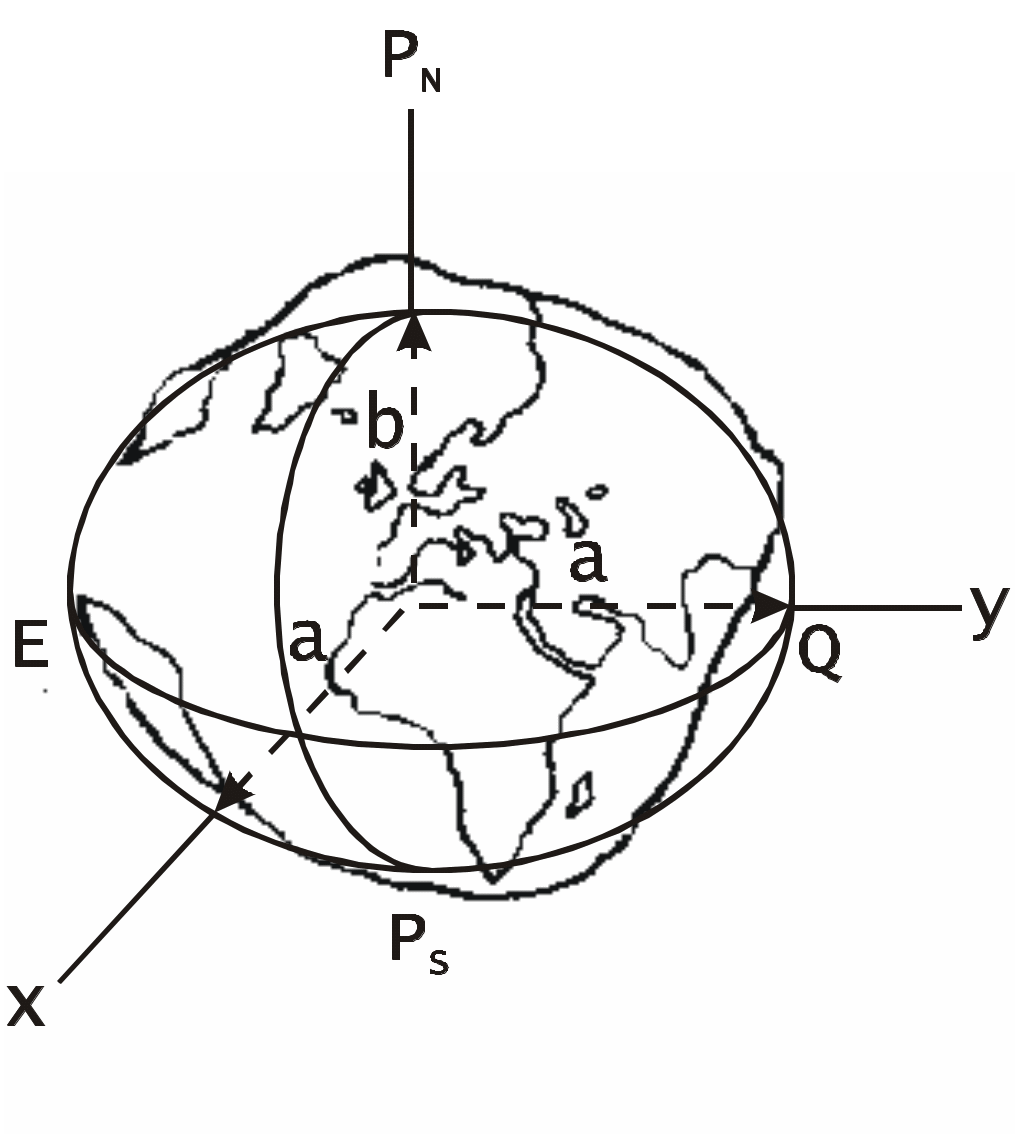



Рис. 1.1. Геоид
уда совершают плавания по водам Мирового океана на поверхности Земли. Поэтому для морской навигации необходимо знать форму и размер Земли. Форма Земли уникальна и не совпадает ни с одной из известных геометрических форм. Неправильность формы Земли обусловлена неравномерным распределением плотности масс в её толще. Фигура Земли называется геоидом. В переводе с греческого геоид означает “землеподобный” (рис. 1.1). Геоид это неправильное геометрическое тело, ограниченное уровенной поверхностью океанов при полном равновесии, находящихся в них, водных масс. Эта уровенная поверхность всюду горизонтальна, т.е. в любой точке нормаль к ней совпадает с отвесной линией; она непрерывная, замкнутая, без складок и рёбер. Геометрия геоида очень сложна и из-за этого обработка измерений, относимых к его поверхности, очень затруднена. Поэтому для решения задач судовождения пользуются наиболее близким к геоиду телом правильной математической формы - эллипсоидом вращения, образованным вращением эллипса вокруг малой оси.

Общеземной эллипсоид удовлетворяет следующим условиям:

1. 
   объем эллипсоида равен объёму геоида;
   
2. 
   большая полуось эллипсоида a совпадает с плоскостью экватора геоида;
   
3. 
   малая полуось b совпадает с осью вращения геоида;
   
4. 
   сумма квадратов уклонений поверхности эллипсоида от поверхности геоида выбрана минимальной.
   

Общеземной эллипсоид практически совпадает со сфероидом - фигурой равновесия вращающейся жидкой массы. Разность по высоте их поверхностей составляет всего 2-3 метра. Поэтому понятие “земной сфероид” и “земной эллипсоид” тождественны. Вид земного сфероида характеризуется полярным сжатием, т.е. отношением разности полуосей эллипсоида к большой полуоси

(1.1)

Вместо полярного сжатия часто пользуются эксцентриситетом

(1.2)

или его квадратом

(1.3)

Связь  и е:

, , .

Следовательно

, , ,



или приближённо

e²  2.

Используя уравнения эллипсоида вращения, можно сравнительно просто математически обработать измерения, произведённые на поверхности Земли.

Из-за различия фигур геоида и эллипсоида вращения нельзя подобрать эллипсоид, который одинаково совпадал бы с геоидом во всех точках уровенной поверхности. Поэтому в разных странах за фигуру Земли принимают такие эллипсоиды, размеры которых в наибольшей степени совпадают с геоидом на территории данной страны.

Эллипсоид с определёнными размерами, определённым образом ориентированный в теле Земли, к поверхности которого относятся результаты геодезических и топографических работ в государстве называется референц-эллипсоидом.

Из-за различия референц-эллипсоидов координаты одних и тех же точек на картах, изданных в разных странах, могут не совпадать. Поэтому переход с карты на карту должен осуществляться не по координатам, а по пеленгу и расстоянию до какого-либо точечного ориентира, нанесённого на обеих картах.

В СССР до 1946 г. использовался референц-эллипсоид Бесселя, выведенный ещё в 1841 г. В России используется референц-эллипсоид Ф.Н.Красовского, имеющий следующие параметры:

1. 
   большая полуось a = 6 378 245 м;
   
2. 
   малая полуось b = 6 356 863 м;
   
3. 
   полярное сжатие
   
4. 
   эксцентриситет .
   

Максимальное отклонение данного эллипсоида от геоида на территории России не превышает 150 м.

Для решения задач определения места судна с помощью глобальных радионавигационных и спутниковых систем используются международные референц-эллипсоиды, у которых отклонения от поверхности геоида в целом минимальны.

В спутниковых навигационных системах (СНС) первого поколения (Транзит, Цикада) использовался эллипсоид WGS - 72 (World Geodetic System - 1972), в настоящее время применяется более точные модели WGS – 84 в СНС GPS (NAVSTAR) и ПЗ-90 (PZ-90) в СНС ГЛОНАСС. Последние исследования показали, что Земля имеет форму апиоида (pear – груша).

Если на судне используются координаты, полученные по автоматизированному приёмоиндикатору радионавигационной или спутниковой систем и рассчитанные на усреднённом международном эллипсоиде, то для определения места судна на навигационной карте, составленной на другом референц-эллипсоиде, необходимо ввести поправки к таким координатам. Подробнее об этом см. в п. ...

При решении задач навигации, не требующих высокой точности, Землю принимают за шар, объём которого равен объёму земного эллипсоида:

(1.4)

Отсюда для референц-эллипсоида Ф.Н.Красовского радиус Земли, как шара, равен R= 6 371 110м.

Системы координат

Для ориентации наблюдателя на поверхности Земли приняты следующие условные точки, линии и плоскости. (Рис. 1.2).

З
Рис. 1.2. Земной сфероид
емной осью называется воображаемая линия P_NP_S, вокруг которой происходит вращение Земли. Эта ось совпадает с малой осью земного сфероида.

Географическими полюсами P_N и P_S называются точки пересечения земной оси с поверхностью Земли. Полюс P_N, откуда вращение Земли усматривается против часовой стрелки, называется северным, его антипод P_S - южным.

Параллелями ВВ₁ называются малые круги на поверхности сфероида, образованные пересечением сфероида плоскостями перпендикулярными к земной оси.

Экватором ЕQ называется большой круг, образованный на поверхности сфероида, при пересечении его плоскостью перпендикулярной к земной оси и проходящей через центр Земли. Экватор делит Землю на два полушария: северное и южное.

Г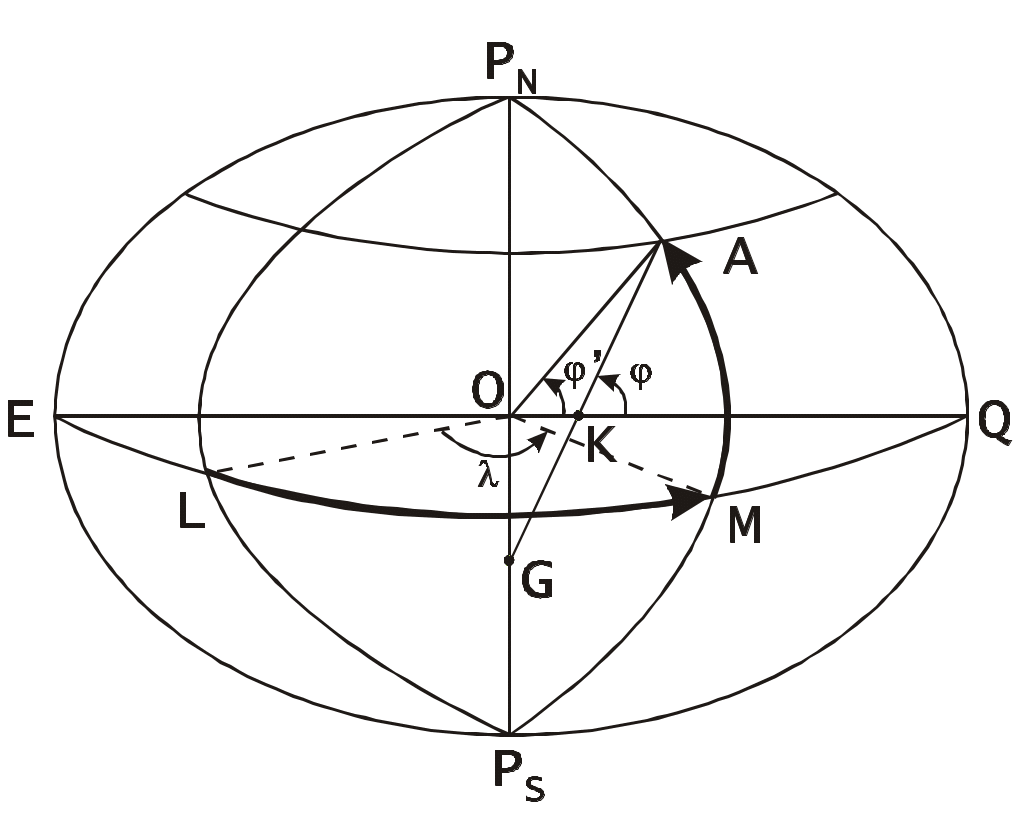
Рис. 1.3. Географическая и сферическая системы координат
еографическими или истинными меридианами P_NBEP_S, P_NBМP_S, P_NB₁QP_S и т.п. называются большие круги, образованные на поверхности сфероида при пересечении их плоскостями, проходящими через земную ось.

Истинным меридианом наблюдателя P_NAМP_S (Рис. 1.3) называется меридиан, проходящий через место наблюдателя А.

Соответствующие плоскости называются: плоскость параллели, плоскость экватора, плоскость истинного меридиана.

Отвесной линией называется прямая, совпадающая с направлением силы тяжести в данной точке.

Положение точки на земной поверхности определяется двумя координатами. Существуют несколько систем координат: географическая, сферическая, геодезическая, астрономическая, квазигеографическая, геоцентрическая, система с приведённой широтой, прямоугольная и полярная. Географическая система в навигации является основной системой координат на земном сфероиде.

Координатными осями в этой системе служат экватор ЕQ (Pис. 1.3) и начальный (нулевой) меридиан, за который в 1884 г. решением Международной конференции в Вашингтоне, принят Гринвичский меридиан, проходящий через пассажный прибор Гринвичской обсерватории, близ Лондона. Гринвичский меридиан делит Землю на два полушария: восточное и западное.

Координатными линиями в этой системе являются параллели и меридианы, а координатами - широта и долгота.

Географической широтой  называется угол между плоскостью экватора и нормалью (отвесной линией) к поверхности земного сфероида. Широта измеряется дугой меридиана от экватора до параллели данной точки. Все точки на одной параллели имеют одинаковую , т.к. нормали в любой точке параллели пересекут ось вращения Земли в одной точке G. Счет географических широт ведётся в градусах, минутах, и десятых долях минуты ( или в секундах) от 0 на экваторе до 90на полюсах. Широтам в северном полушарии приписывается наименование Nord (N) или знак “+” (при расчётах), широтам в южном полушарии - наименование Sud (S) или знак “”. Например:





В ручных навигационных расчётах и записях во избежание ошибок, не принято опускать математический знак “+”.

Географической долготой  называется двугранный угол между плоскостью начального (нулевого) меридиана и плоскостью меридиана, проходящего через данную точку. Долгота измеряется меньшей из дуг экватора от Гринвичского меридиана до меридиана данной точки. Все точки на одном меридиане имеют одинаковую долготу. Счёт географических долгот ведётся в градусах, минутах и десятых долях минуты (или в секундах) от 0 на Гринвичском меридиане до 180. Долготам в восточном полушарии приписывается наименование East (Е) (читается “ост”) или знак “+” (при расчётах), долготам в западном полушарии - West (W) или знак “”. Например:





Если при расчётах долгота получается больше 180, то необходимо взять её дополнение до 360 и поменять наименование на обратное. Например:



Меридиан 180 принят как международная линия перемены дат.

Сферическая система. Если принять Землю за шар, то географическая система координат превращается в сферическую. В этом случае нормаль к поверхности Земли (сферы) совпадает с направлением на центр сферы.

Геодезическая система относится к поверхности референц-эллипсоида. Геодезические широта (В) и долгота (L) определяются относительно пунктов государственной геодезической сети, исходным пунктом которой в России принят центр Круглого зала Пулковской обсерватории близ Санкт-Петербурга.

Различие геодезической и географической систем координат состоит в том, что геодезические координаты определяются геодезическим способом, а географические могут быть определены любым из существующих способов.

Астрономическая система. В ней используются те же координаты, что и в географической системе, но отнесённые не к земному сфероиду, а к геоиду. Расхождения между географическими и астрономическими координатами очень малы и в практике судовождения не учитываются.

Квазигеографическая система. Отличается от географической тем, что квазиполюсы этой системы Pq_N и Pqs смещены на 90 относительно географических полюсов, т.е. располагаются на экваторе (Рис.1.4). Координатными осями считаются квазиэкватор, являющийся меридианом 90Е - 90W и начальный квазимеридиан, совпадающий с меридианом 0-180. Координатными линиями являются квазипараллели и квазимеридианы, а координатами квазиширота _q и квазидолгота _q.

С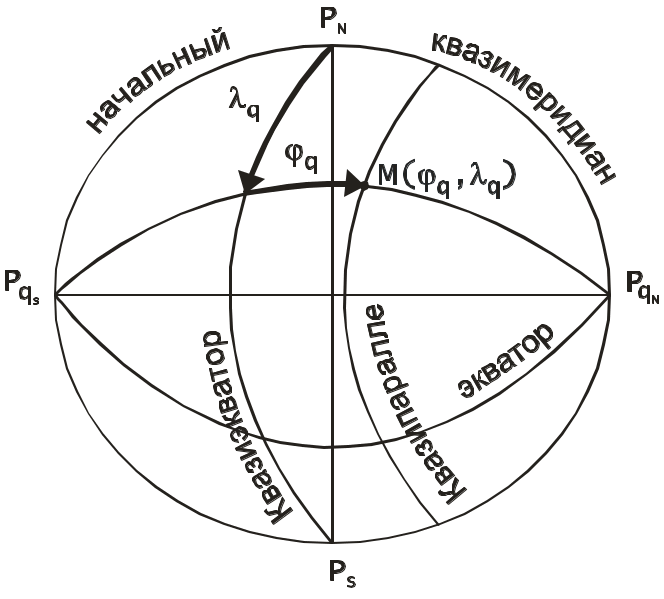
Рис. 1.4. Квазигеографическая система координат
истема используется для построения карт приполюсных районов. (Подробнее см. разд. )

Геоцентрическая система. Одной из координат является географическая или геодезическая долгота. Другой координатой является геоцентрическая широта (Рис1.3) - угол AOQ между плоскостью экватора и радиус-вектором, проходящим через центр Земного сфероида. Геоцентрическая широта  в общем случае меньше . Разность между географической и геоцентрической широтами называется редукцией широты

, (1.5)

где   полярное сжатие,   географическая широта.

М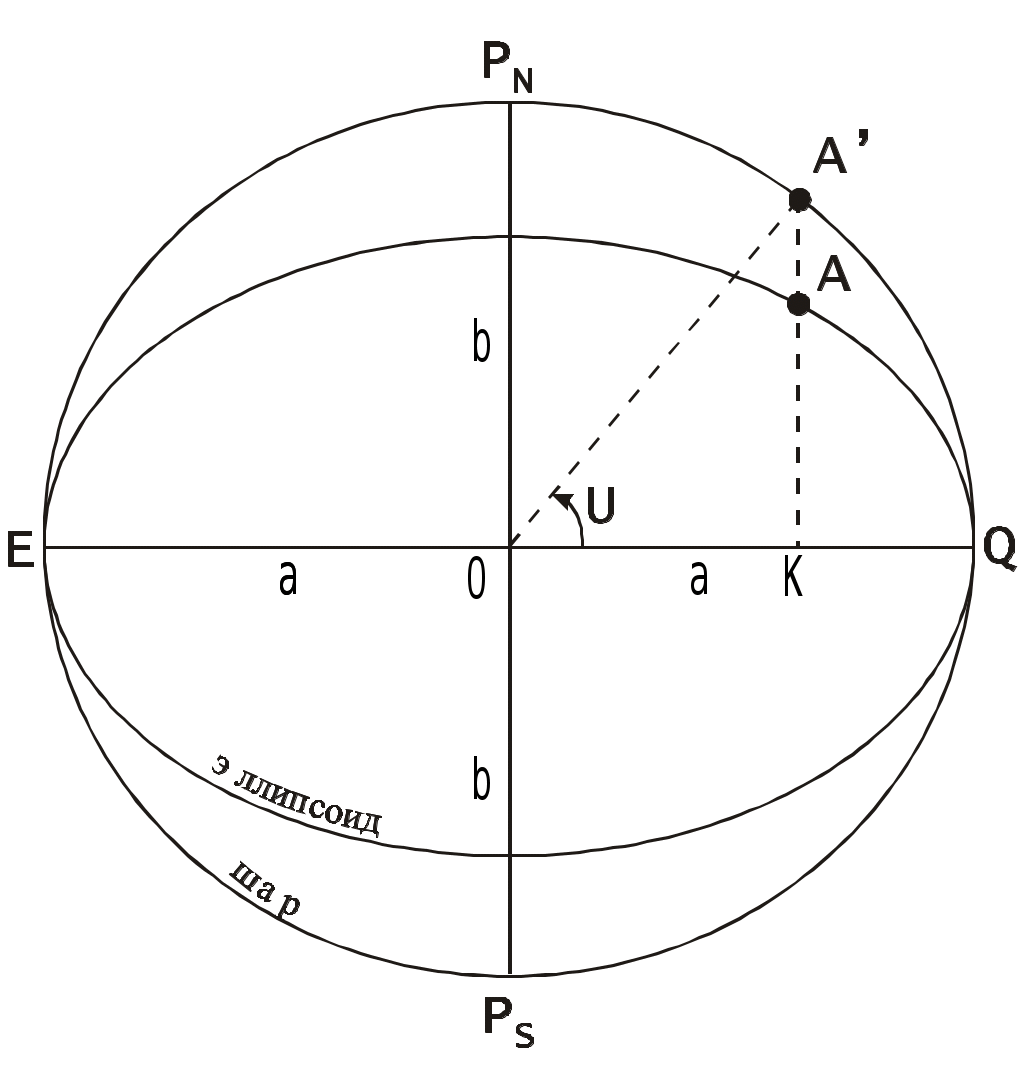
Рис. 1.5. Система с приведенной широтой
аксимального значения редукция достигает в  = 45, где она равна 1127”. В  = 0 и 90 r = 0.

Используется в некоторых дисциплинах, смежных с навигацией.

Система с приведённой широтой. Одной из координат является географическая или геодезическая долгота. Другой координатой является приведённая широта U (Рис.1.5).

Для получения приведённой широты опишем окружность радиусом равным большой полуоси a земного сфероида. Через точку А проведём прямую АК, параллельную земной оси, и продолжим её до пересечения с окружностью в точке А. Центральный угол между плоскостью экватора и радиусом-вектором АОQ называется приведённой широтой.

Связь географической и приведённой широт определяется формулой

(1.6)

Приведённая широта применяется в теоретической картографии и при решении навигационных задач по расчёту кратчайших расстояний и азимутов на поверхности земного сфероида.

П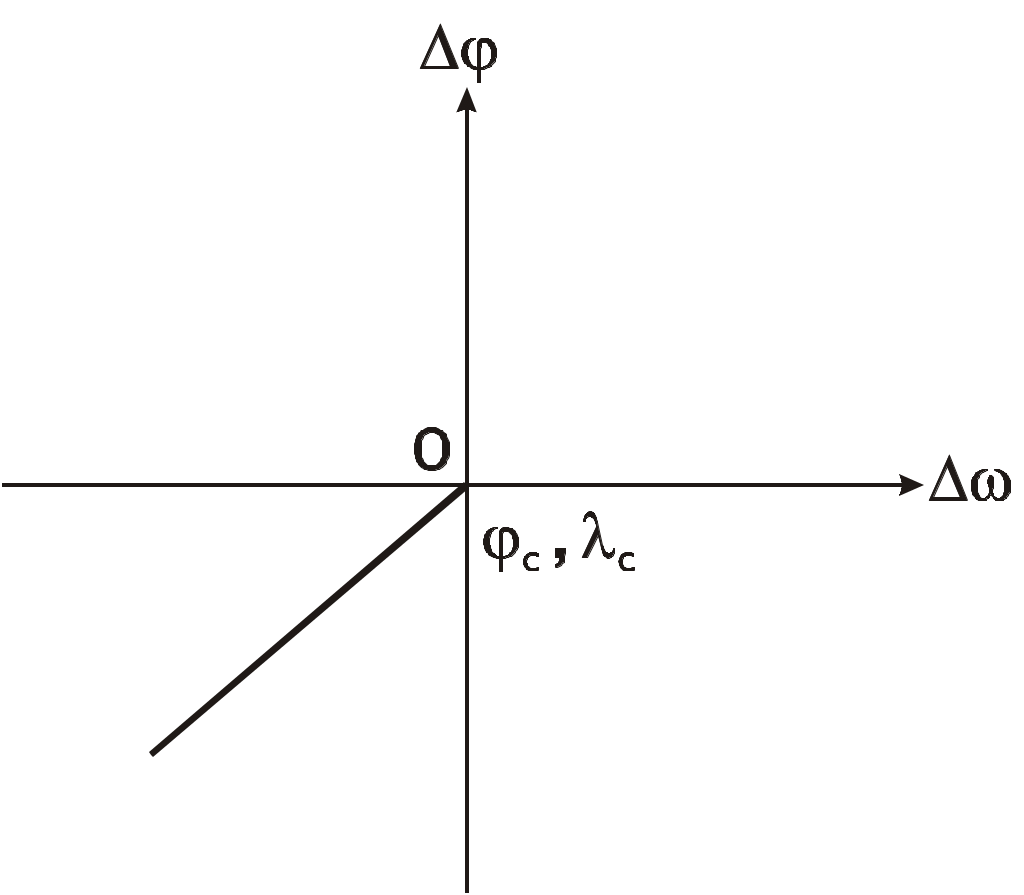
Рис. 1.6. Локальная система координат
рямоугольная система. Координатами являются величины X и Y, представляющие собой удаление данной точки в метрических единицах длины от экватора и от одного из меридианов, принятого за осевой. Система используется при топографических работах и составлении топографических карт, а также для нанесения километровой сетки на карты в проекции Гаусса и морские навигационные карты в проекции Меркатора.

Полярная система. Используется для определения положения заданной точки по направлению и расстоянию относительно другой точки. Обычно полярная система координат применяется для определения места судна относительно подвижного объекта.

Локальная система координат ,  с началом 0 в счислимой точке _с, _с применяются для решения задач определения места судна методом линий положения (Рис.1.6).
Р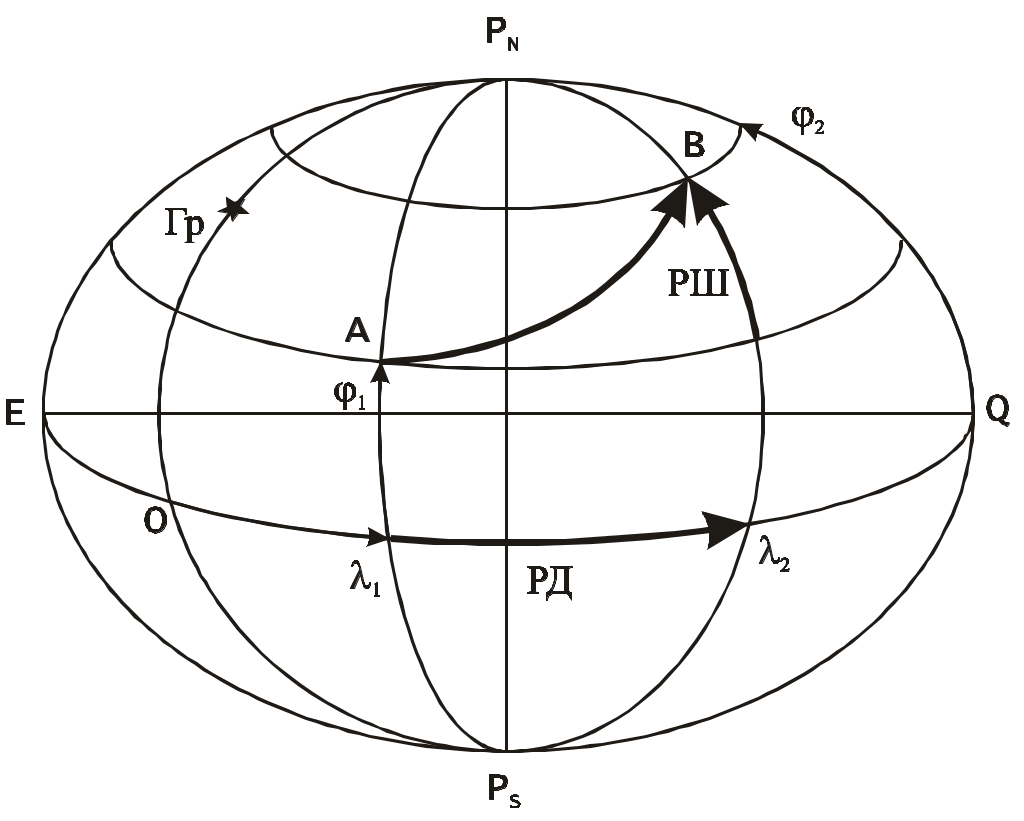
Рис. 1.7. Разность широт и разность долгот
азность широт и разность долгот
Перемещение точки в любой координатной системе определяется приращением координат. В географической системе координат это приращение широты и долготы, которые в морской навигации называются разностью широт и разностью долгот.

На рис. 1.7 судно из точки А с координатами ₁ и ₁ перешло в точку В с координатами ₂ и ₂.

Разностью широт (РШ, ) называется дуга меридиана, заключённая между параллелями пункта отхода (₁) и пункта прихода (₂).

Разность широт измеряется в пределах от 0 до 180 и имеет наименование “к N” (или знак “+”), если параллель пункта прихода лежит севернее параллели пункта отхода, независимо от того в каком полушарии северном или южном находятся точки отхода и прихода, и “к S” (или знак “”), если параллель пункта прихода лежит южнее параллели пункта отхода.

Разность широт и её знак определяются по формуле

(1.7)

Формула (1.7) алгебраическая, т.е. широты ₁ и ₂ подставляются в неё со своими знаками.

Разностью долгот (РД, ) называется меньшая из дуг экватора, заключённая между меридианами пункта отхода (₁) и пункта прихода (₂).

Разность долгот измеряется в пределах от 0 до 180 и имеет наименование “к Е”(или знак “+”), если меридиан пункта прихода лежит восточнее меридиана пункта отхода, независимо от того в каком полушарии восточном или западном находятся точки отхода и прихода, и “к W” (или знак “”), если меридиан пункта прихода лежит западнее меридиана пункта отхода.

Разность долгот и её знак определяются по алгебраической формуле

(1.8)

Если в результате расчета по формуле (1.8) РД получится больше 180 , то необходимо взять её дополнение до 360 и поменять наименование (знак) на противоположное.

В формулах (1.7) и (1.8) неизвестными аргументами могут быть три варианта решения навигационных задач. Наиболее часто используются варианты, показанные на нижеследующих примерах.