Вся навигация. вся навигация 1. Фигура и модели Земли
 Скачать 3.45 Mb. Скачать 3.45 Mb.
|
|
Пример. Для определения скорости судна на полном ходу, поправки лага и коэффициента лага сделаны два пробега. Длина пробегов, измеренная по РЛС S=3,0 мили, время пробегов t1 = 585c, t2 = 620с, разность отсчётов лага на пробегах РОЛ1 = 2,94 и РОЛ2 = 2,83. Рассчитать среднюю скорость судна относительно воды на полном ходу V0, а также поправку лага и коэффициент лага. Л и Кл рассчитать по: приближённым формулам (1.59), (1.62) (1.79) и (1.80); по формулам для двух пробегов (1.77) и (1.78), с использованием V0 и замене Sл = V0ti по формулам (1.84) - (1.86), с использованием V0 и Vл по формулам(1.81)-(1.84). Решение: 1. 2. 3. 4. Как видно постоянное течение можно исключить полностью, если сделать два пробега и вести судно по компасу. Если же течение изменяется, то исключить его влияние полностью нельзя, можно только уменьшить его влияние. 3. Если на мерной линии течение меняется равномерно, т.е. течение имеет постоянное ускорение т , то делают три пробега: два в одном направлении и одно в обратном. Первый пробег по направлению течения: V1 = V0 + т Второй пробег в обратном направлении: V2 = V0 (т + т) 2 Третий пробег по направлению течения: V3 = V0 + (т + 2т ) V  1 + 2V2 + V3 = 4 V0, 1 + 2V2 + V3 = 4 V0,Отсюда Частота вращения винтов, соответствующая скорости V0 рассчитывается по аналогичной формуле Формула (1.87) приближённая, она не учитывает, что время пробегов и время поворотов при таком течении разное. Более точную формулу можно получить воспользовавшись идеей академика А.Н. Крылова о том, что проекция вектора скорости течения на линию ИК меняется линейно во времени: где т - проекция скорости течения на линию ИК в момент времени t; Сделав один пробег, и определив относительную скорость без учёта течения, т.е. с погрешностями, вносимыми течением: получим выражение где Выражение (1.91) частично учитывает изменение вектора скорости течения на первом пробеге и поэтому оно более точное, чем (1.90). Сделав второй пробег и определив относительную скорость без учёта течения по формуле аналогичной (1.90), получим выражение где В выражении (1.93) Т1 - время между окончанием первого и началом второго пробега, t2 / 2 - средний момент второго пробега. Использование среднего времени tср2 даёт частичный учёт течения. Третий пробег в направлении первого даёт ещё одно уравнение: где В выражении (1.95) Т2 - время между окончанием второго и началом третьего пробега, t3 / 2 - средний момент третьего пробега. Вычтя из выражения (1.94) выражение (1.91), можно найти коэффициент k: Сложив уравнения (1.91) и (1.92), можно получить более точную формулу определения относительной скорости судна: 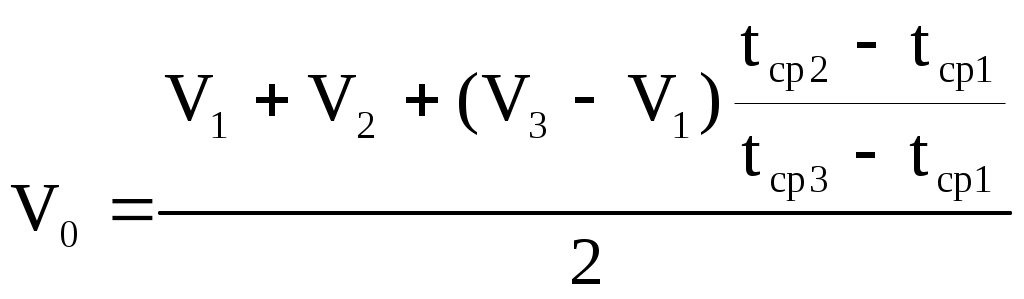 (1.97) (1.97)Уравнение (1.97) или приближённая формула (1.87) используются для определения Л и КЛ по формулам (1.81) и (1.83) и (1.85 1.86). Для трёх пробегов: Поправку лага и коэффициент лага можно также рассчитать по приближённым формулам: где Лi и Клi рассчитываются по формулам (1.59) и (1.62). Пример. Для определения скорости судна, поправки лага и коэффициента лага на мерной линии сделаны три пробега. Длина пробега между секущими створами S=2,5 мили, время пробегов t1 = 521c, t2 = 577c, t3 = 544c, разность отсчётов лага РОЛ1=2,62, РОЛ2=2,55 и РОЛз=2,58. Рассчитать среднюю скорость судна относительно воды на полном ходу V0, а также поправку лага и коэффициент лага. Л и Кл рассчитать по: 1) приближённым формулам (1.59), (1.62), (1.79) и (1.80), 2) с использованием V0 и замене Sл = V0ti по формулам (1.84) (1.86), 3) с использованием V0 и Vл по формулам (1.81) (1.84). Решение: 1. 2. 3. 4. Если течение на мерной линии меняется неравномерно, то делают четыре пробега. Первый пробег по направлению течения: V1 = V0 + т Второй пробег в обратном направлении: V2 = V0 (т + т)3 Третий пробег по направлению течения: V3 = V0 + (т + 2т + т)3 Четвёртый пробег в обратном направлении: V4 = V0 (т + 3т + 2т +т) V  1 + 3V2 + 3Vз + V4 = 8V0 + т т 1 + 3V2 + 3Vз + V4 = 8V0 + т тОтсюда Как видно из формулы (1.100) даже при четырёх пробегах в расчётную величину Vo входит и неисключаемая часть влияния течения. Приближенная формула позволяет частично скомпенсировать непостоянство вектора ускорения течения. Частота вращения винтов, соответствующая V0 определяется формулой а поправка лага и коэффициент лага рассчитываются по формулам Формулы (1.101), (1.103) и (1.104) не исключают полностью вектор скорости течения, но остаточная систематическая погрешность поглощается случайными погрешностями измерений, поэтому эти формулы практически работоспособны. Точность определения скорости на мерной линии можно получить из формулы где ms и mt - средние квадратические погрешности соответственно длины пробега (в милях) и продолжительности пробега (в с). В этой формуле погрешностями, оставшимися от исключения течения по их малости, пренебрегли. Из формулы (1.105) видно, что mvo зависит от длины пробега S. Так как расстояние между секущими створами известно с высокой точностью, то можно принять ms= 0. Чтобы получить скорость судна с относительной погрешностью не более 0,5%, при предельной погрешности в определении времени пробега равной 2 СКП в 1,5с, длина пробега определяется формулой Формулу точности определения поправки лага в %, получим продифференцировав формулу (1.59) 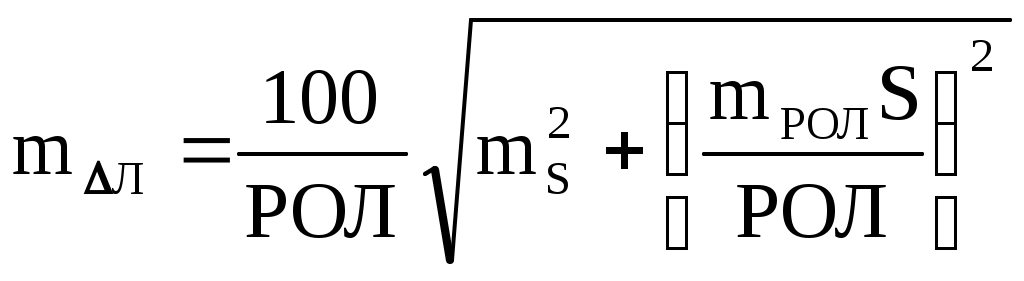 , (1.107) , (1.107)где mрол - средняя квадратическая погрешность разности отсчёта лага, мили. Полагая ms = 0, получим Так как поправка лага обычно невелика и не превышает нескольких процентов, то можно принять, что РОЛ S .Тогда формула (1.108) примет вид Чтобы получить Л с предельной погрешностью 0,5%, длина пробега должна быть не менее 1,5 мили. Для повышения точности результатов скоростных испытаний наблюдать за створами надо в бинокли или оптические пеленгаторы, а засекать моменты пересечения створов секундомерами. Желательно, чтобы моменты пересечения створа наблюдали три наблюдателя, каждый самостоятельно и со своим секундомером. С 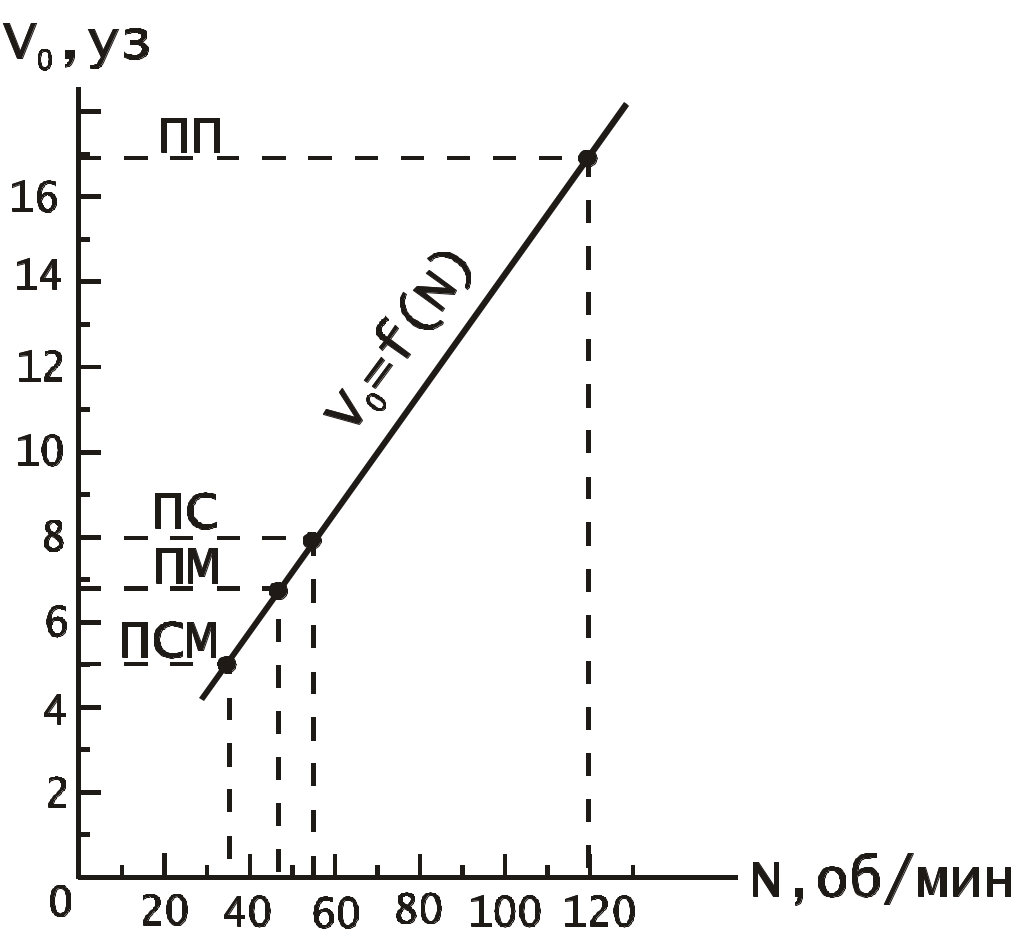 Рис. 1.36. График соответствия скорости судна частоте вращения винтов 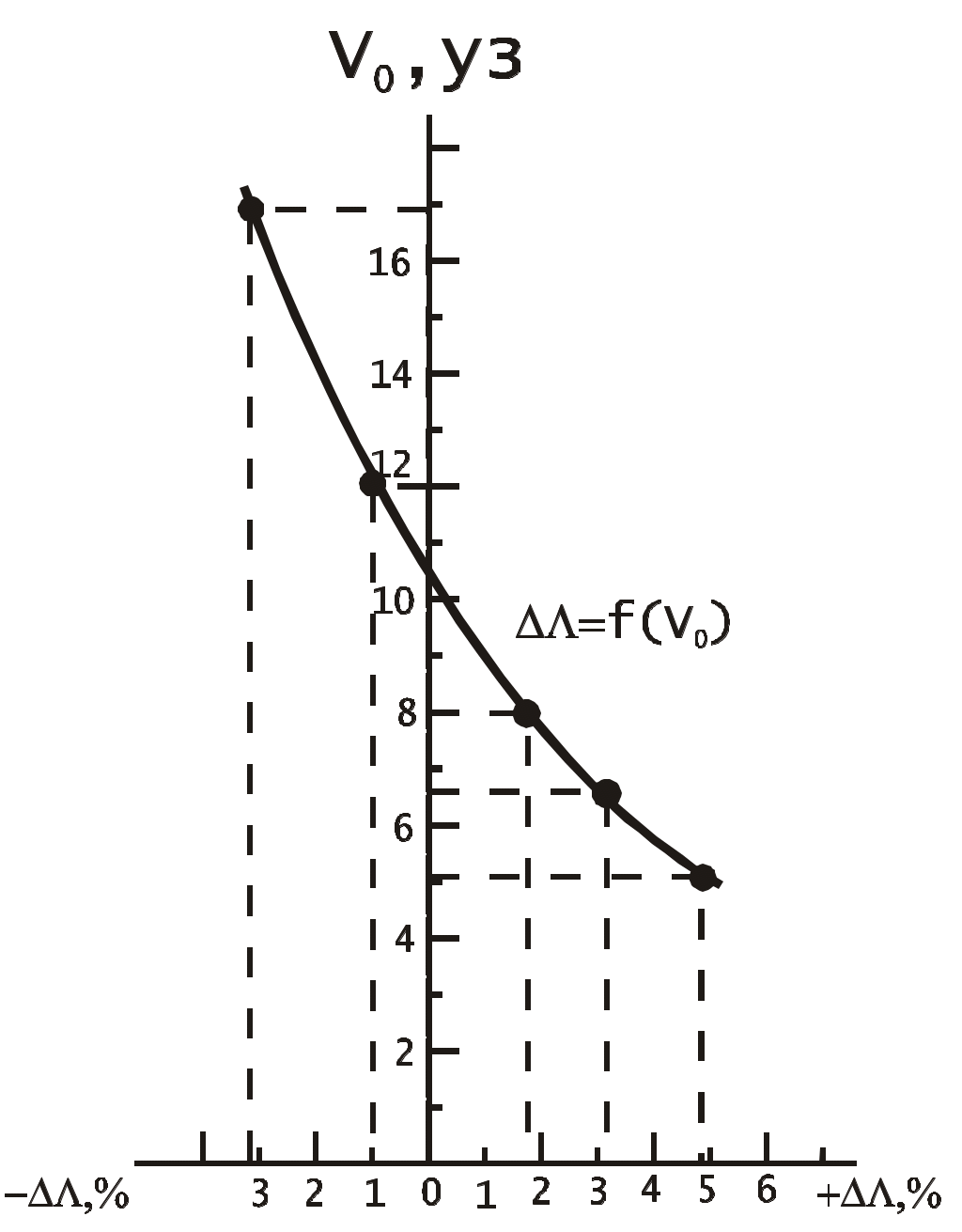 Рис. 1.37. График зависимости поправки лага от скорости судна Рис. 1.37. График зависимости поправки лага от скорости суднакоростные испытания проводятся для всех режимов работы двигателя:: полного, среднего, малого и самого малого хода - для судна в полном грузу и в балласте. По результатам скоростных испытаний строят графики соответствия скорости судна, частоте вращения винтов (рис.1.36) и зависимости поправки лага от скорости судна (рис.1.37). П  о снятым с графика данным составляется таблица соответствия скорости частоте вращения винтов (табл.1.3) и таблица поправок лага, в зависимости от скорости (табл.1.4). о снятым с графика данным составляется таблица соответствия скорости частоте вращения винтов (табл.1.3) и таблица поправок лага, в зависимости от скорости (табл.1.4).Табл. 1.3 Табл. 1.4
Для контроля проведённых скоростных испытаний вычерчивают график изменения скорости течения (точнее вектора скорости течения на линию пробега) во времени. В случае равномерного изменения скорости течения и отсутствия погрешностей в вычислениях график должен получиться в виде плавной кривой. На судах, оборудованных гребными винтами регулируемого шага (ВРШ), скоростные испытания проводят при нескольких положениях лопастей для каждой скорости. Если скорость судна относительно воды V1 известна только для одного соответствующего N1, то для прогнозирования относительной скорости V2 соответствующей числу оборотов N2, можно воспользоваться эмпирическими формулами инж. Афанасьева 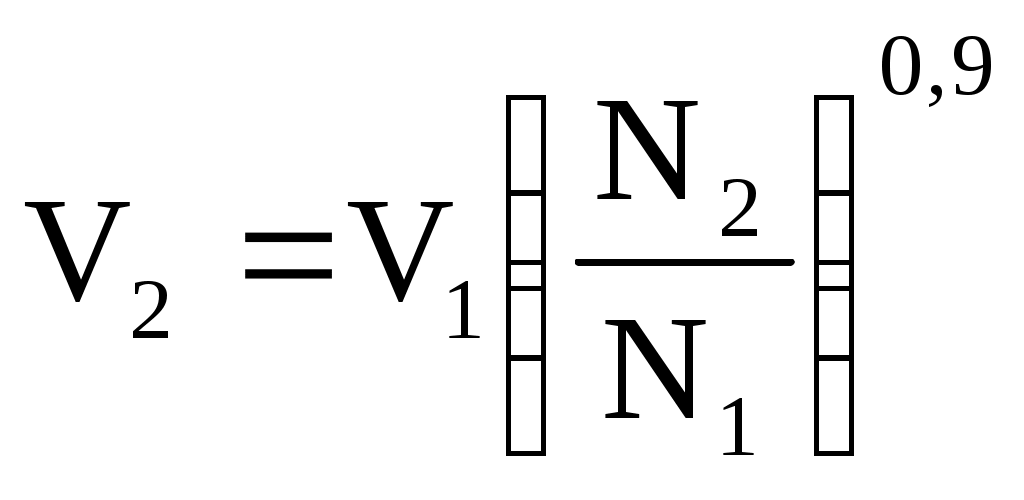 - для поршневых машин - для поршневых машини 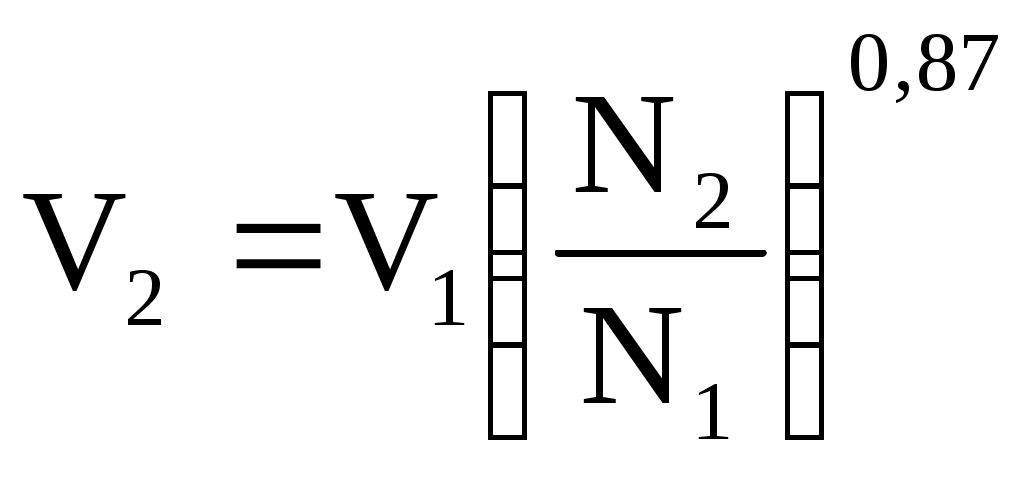 - для турбинных установок. - для турбинных установок. |
