Вся навигация. вся навигация 1. Фигура и модели Земли

• Название: Фигура и модели Земли
• Анкор: Вся навигация
• Дата: 31.01.2023
• Размер: 3.45 Mb.
• Имя файла: вся навигация 1.doc
• Тип: Документы; #913997
• страница: 7 из 9

Определение скорости и поправки лага с помощью радиолокационной станции (РЛС)

Скорость судна V₀ и поправку лага Л можно определить с помощью РЛС и свободно плавающего буя или вехи. При этом действие течения исключается даже на одном пробеге, т.к. свободно плавающий буй или веха перемещаются под действием течения почти также как и судно. Приводят ориентир на КУ = 0 и дважды через 3 - 4 мили измеряют расстояние до него (D₁ и D₂), фиксируя при этом моменты времени по секундомеру и показания суммарного счётчика оборотов.

Формула расчёта скорости судна относительно воды на пробеге (1.69) примет вид

(1.110)

Частота вращения винтов на пробеге определяется по формуле (1.68). Точность определения V₀ рассчитывается по формуле (1.105), в которой m_S=m_D и S=(D₁-D₂)=D:

(1.106)

Формула поправки лага (1.59) примет вид

(1.111)

Точность определения поправки лага рассчитывается по формуле (1.107). Длина пробега для определения Л с предельной ошибкой 0,5% составляет  3,5 мили, если Л определяется на двух пробегах, и 3 мили - на трёх пробегах.

Д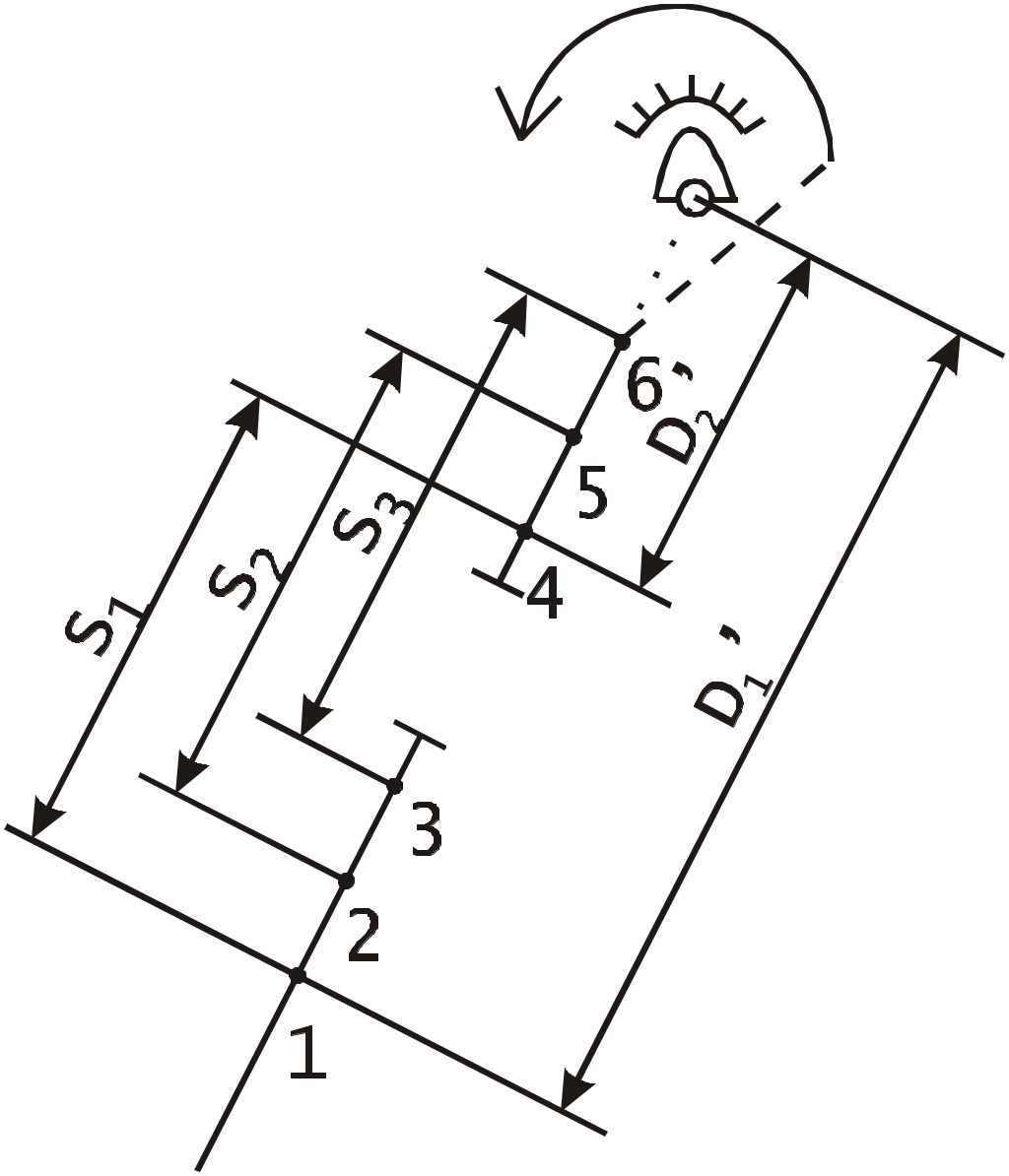
Рис. 1.38. Определение скорости и поправки лага с помощью РЛС
ля существенного уменьшения влияния случайных ошибок наблюдений целесообразно произвести не однократное, а трёхкратное измерение S, РОЛ, N и Т. Для чего, установив ПКД в начале пробега на выбранное расстояние D₁^ , в момент, когда эхо-сигнал коснётся ПКД (точка 1 на рис.1.38), замечают ОЛ₁ и включают первый секундомер. Затем дважды последовательно уменьшают расстояние на ИКО на 1-2 кб и в моменты касания эхо-сигнала ориентира с ПКД (D₁^ и D₁^) в точках 2 и 3 замечают ОЛ₁^ и ОЛ₁^ и включают второй и третий секундомеры. После этого устанавливают ПКД на расстояние, меньшее первоначального на 3-4 мили, т.е. на расстояние равное необходимой длине пробега, и в момент касания эхо-сигнала

ориентира с ПКД (D₂^) в точке 4 замечают ОЛ₂ и останавливают первый секундомер. Затем дважды последовательно уменьшают расстояние на ИКО на 1-2 кб и в моменты касания эхо-сигнала ориентира с ПКД в точках 5 и 6 замечают ОЛ₂^ и ОЛ₂^ и останавливают соответственно второй и третий секундомеры (рис.1.38).

В формулы (1.110) и (1.111) подставляются средние значения

, ,



Аналогично рассчитывается и N.

Скорость и поправку лага можно определить и по стационарному бую или судну, стоящему на якоре. Но в этом случае для уменьшения влияния течения надо сделать несколько пробегов, в зависимости от характера течения. Обычно при таких определениях целесообразно делать три пробега. Если угол сноса судна будет более 2, фактические длины пробегов S_i не будут равны полученным по РЛС разностям расстояний . Д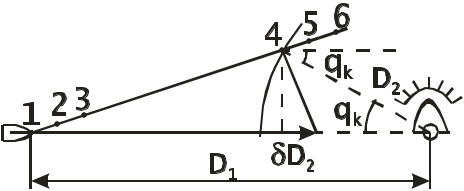ля уточнения длины пробегов S_i надо конечные расстояния D₂^, D₂^ и D₂^ исправить поправками равными

, (1.112)

г
Рис. 1.39. Определение фактической длины пробега
де q_k - курсовой угол ориентира в момент измерения конечного расстояния равный ИП  ИК судна (рис1.39).

Если радионавигационная система (РНС) или спутниковая навигационная система (СНС) обеспечивает высокоточные измерения, то можно определить V₀ и Л, используя обсервации, полученные по таким системам.

Определение скорости и расстояния с помощью абсолютного лага

А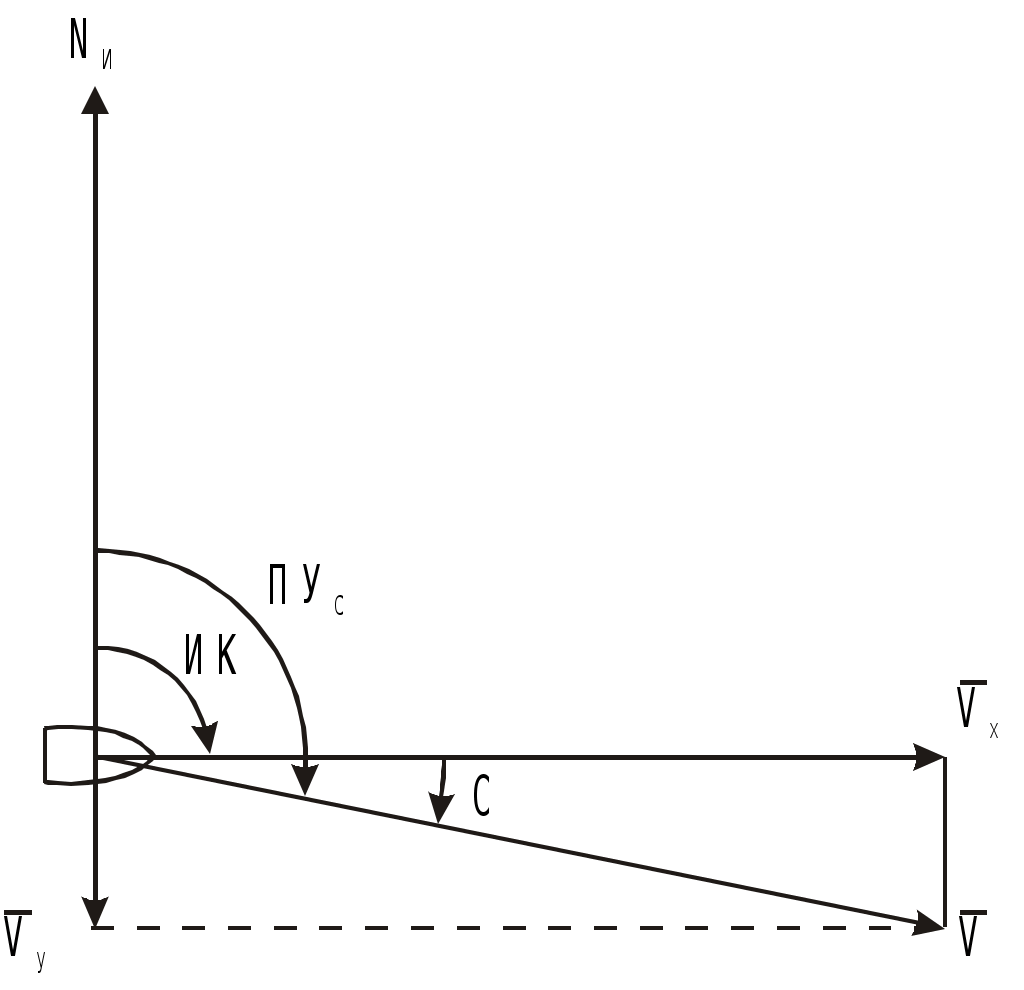
Рис. 1.40. Определение скорости абсолютным лагом
бсолютный лаг измеряет две составляющие абсолютной скорости: продольную V_х и поперечную V_у (рис.1.40). Продольная составляющая V_х направлена по ДП судна и имеет знак “+” при переднем ходе. Поперечная составляющая V_у направлена перпендикулярно ДП судна и имеет знак “+” в направлении правого борта.

Векторное уравнение скоростей:

(1.113)

Модуль вектора V:

(1.114)

Направление вектора V относительно ДП:

, (1.115)

где с - суммарный угол сноса под действием ветра и течения, определяющий направление пути судна .

Абсолютный лаг, как и относительный лаг, имеет методические и инструментальные погрешности. Для учёта систематических погрешностей, остающихся после регулировки лага, необходимо знать две константы, которые определяются на мерной линии по продольному и поперечному каналам.

По оси Х определяется коэффициент абсолютного лага, %,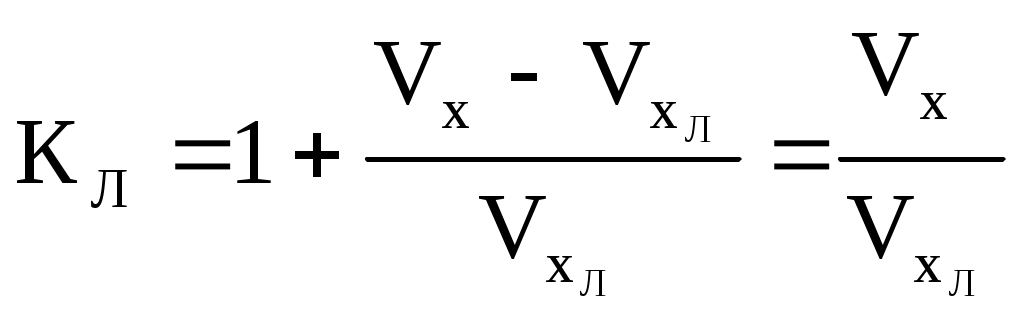

(1.116)

По оси y определяется условный угол разворота системы вибраторов гидроакустических антенн Ра:

, (1.117)

где V_x, V_y - истинные продольная и поперечная составляющие вектора абсолютной скорости V; , - лаговые значения продольной и поперечной составляющих вектора абсолютной скорости Vл.

Исправленные значения составляющих абсолютной скорости:

(1.118)

и

(1.119)

В формулах (1.118) и (1.119) V_x, V_y, и - это средние значения истинных и лаговых составляющих вектора абсолютной скорости из всех пробегов для данного режима хода.

Расстояния, пройденные судном, рассчитываются по формулам:

, (1.120)

, (1.121)

. (1.122)

Так как абсолютный лаг значительно точнее относительного, то и определение его поправок должно производиться с высокой точностью, используя для наблюдений пеленгатор или бинокль с кратностью увеличения не менее двух. Для определения Кл и Ра с высокой точностью используются высокоточные РНС, СНС и теодолитные засечки с берега.

По обсервациям определяют эталонную абсолютную скорость судна и её составляющие, а синхронные измерения курса и показаний лага дают лаговую скорость и её составляющие. Число пробегов для каждого режима скоростей должно быть не менее семи. Увеличение количества пробегов при определении поправок абсолютного лага для исключения влияния течения не требуется. Увеличение числа пробегов на каждом режиме хода необходимо только для повышения точности измерений. Статистической обработкой результатов измерений определяют средние значения оцениваемых параметров и их доверительные интервалы. Затем составляются графики и таблицы поправок в зависимости от скорости судна.

Видимый горизонт и его дальность

Видимость очень важна для безопасности мореплавания. В зависимости от видимости назначается соответствующая скорость судна.

Н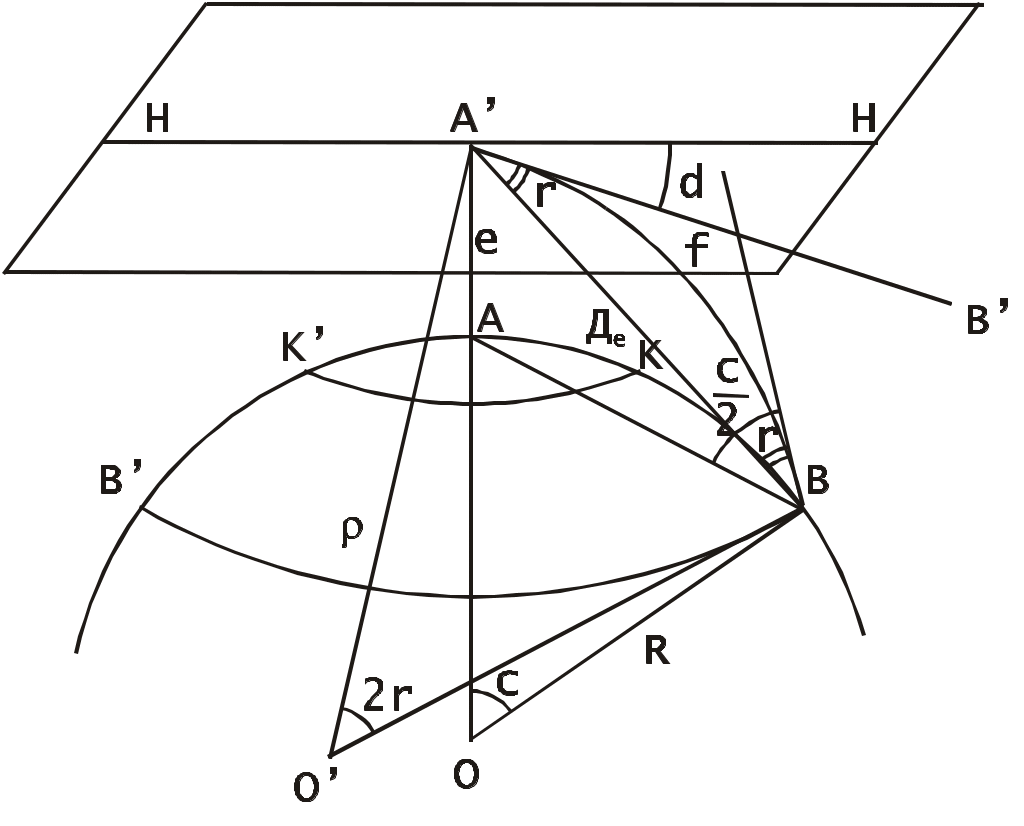
Рис. 1.41. Дальность видимого горизонта
а рис.1.41 представлена поверхность земного шара с радиусом R. В точке A находится глаз наблюдателя на высоте e над точкой А поверхности моря. Лучи зрения, идущие к точке A и касательные к поверхности воды, образуют малый круг КК, называемый теоретически видимым горизонтом. На самом деле наблюдатель будет видеть поверхность воды, ограниченную малым кругом ВВ, называемым видимым горизонтом наблюдателя

Дело в том, что лучи света распространяются не прямолинейно, т.к. плотность атмосферы по высоте различна. Преломление луча света, проходящего через земную атмосферу, называется земной рефракцией. Поэтому луч света от точки B попадёт в глаз наблюдателя, пройдя по кривой BfA, и наблюдатель увидит точку B по направлению АВ приподнятому над линией АВ на угол r, называемый углом земной рефракции.

Вертикальный угол между плоскостью истинного горизонта наблюдателя Н и направлением на видимый горизонт называется наклонением видимого горизонта d.

Кривую, по которой распространяется луч света на небольших расстояниях, можно считать дугой окружности с радиусом .

Отношение радиуса Земли R к радиусу  называется коэффициентом земной рефракции:

(1.123)

Коэффициент земной рефракции характеризует преломляющую способность земной атмосферы. Он определяется практически и величина его изменяется в зависимости от района плавания, времени года и суток, атмосферного давления, температуры и др. факторов. Во всех навигационных пособиях и в таблицах МТ - 2000 принято среднее значение  = 0,16. Максимальное значение коэффициент  имеет при восходе и заходе Солнца. К полудню он быстро уменьшается и с 11 до 14 часов, обычно, величина  соответствуют среднему значению.

Сферический радиус видимого горизонта АВ называется географической или геометрической дальностью видимого горизонта Д_е Эта дальность видимости не учитывает прозрачность атмосферы, считая её идеальной с коэффициентом прозрачности  = 1.

Так как е R то можно принять . Обознач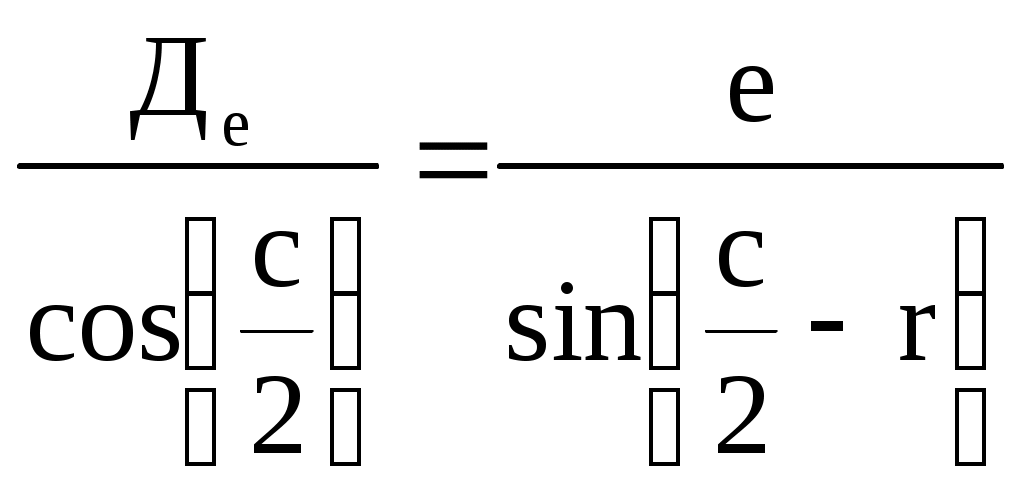им центральный угол при точке О через с. Тогда угол между касательной и хордой АВ равен половине центрального угла с / 2. Т.к. угол между касательной АВ и хордой , то центральный угол при точке

В ОАВ , , . Следовательно, в  AАВ , а . По теореме синусов:



или

_.

Т.к. углы 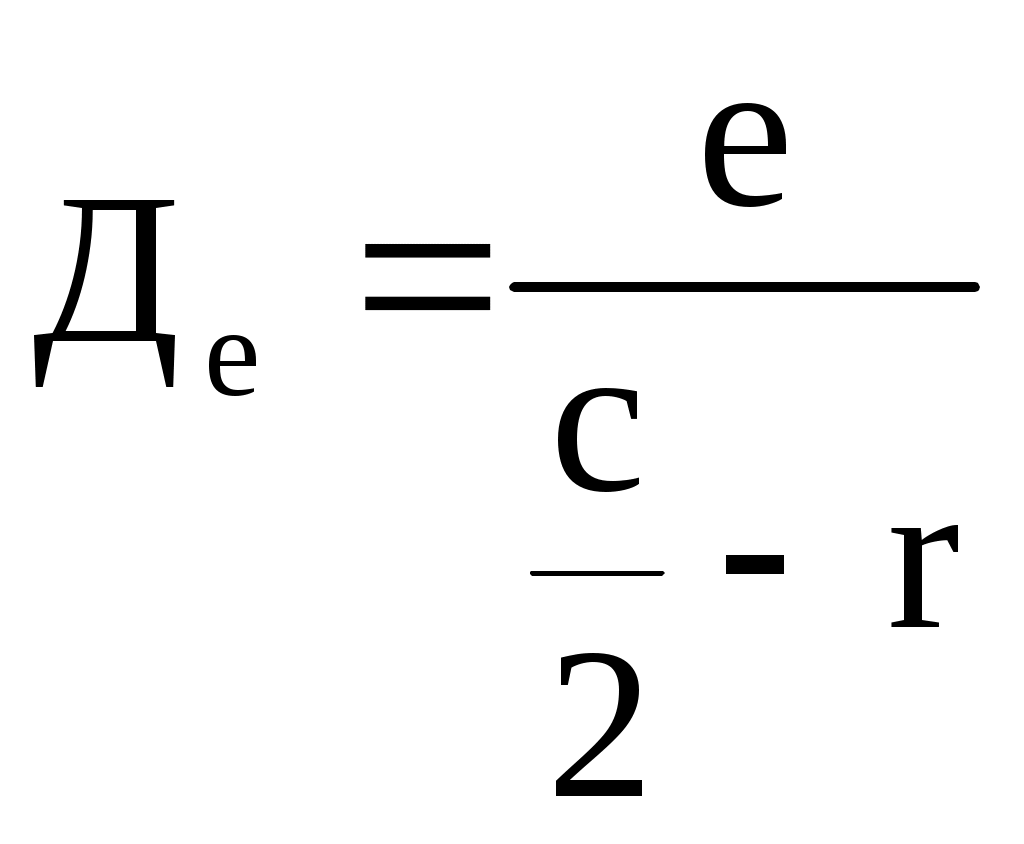 и r малы, то можно заменить самим углом , а принять равным 1. Тогда:

. (1.124)

Углы с и 2r центральные. Поэтому 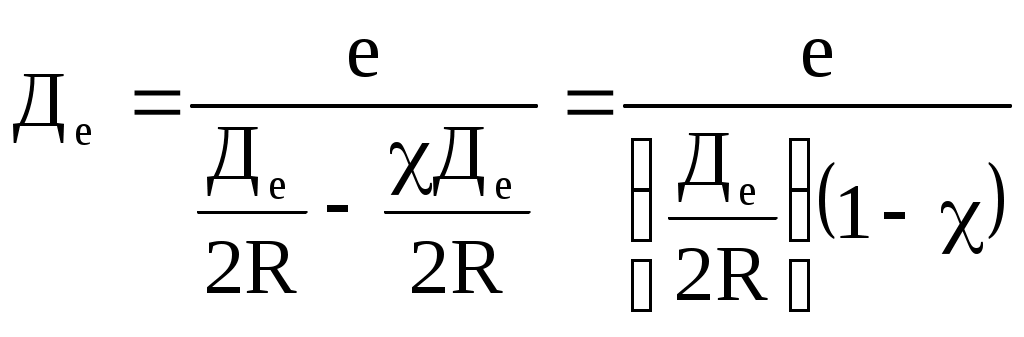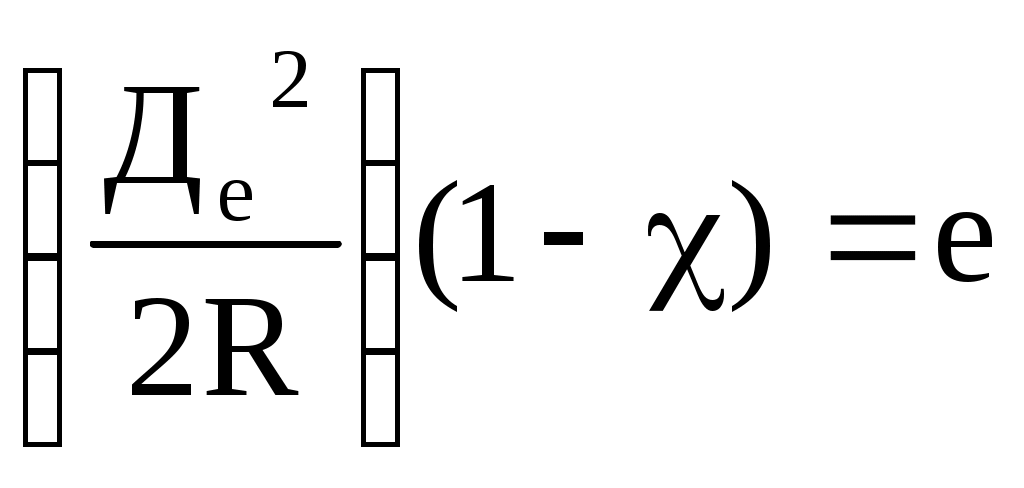и , а и . Умножим и разделим последнее выражение на R. Тогда: Подставим полученные значения и r в формулу (1.124). Получим:

, ,



Приняв радиус Земли R= 3437,747 мили, для получения Д_е в милях при высоте глаза е в метрах разделим на 1852 м. Тогда

,

получим:

, мили (1.125)

По приближенной формуле составлена табл. 2.1 “Дальность видимого горизонта” в МТ - 2000.

Географическая дальность видимости предметов

Г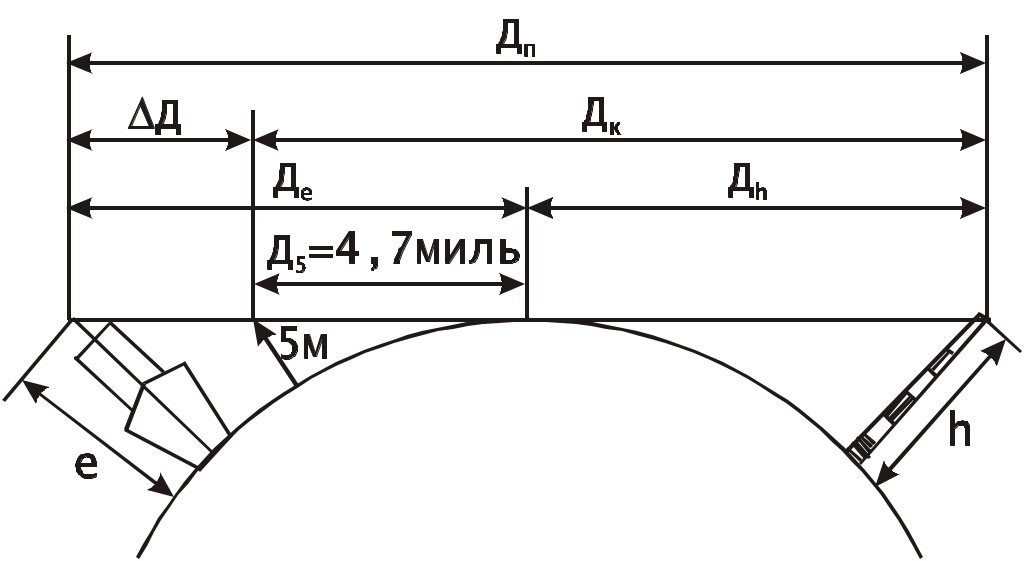
Рис. 1.42. Географическая дальность видимости предметов
еографическая дальность видимости предметов в море Д_п определяется наибольшим расстоянием, на котором наблюдатель увидит его вершину над линией горизонта, т.е. зависит только от геометрических факторов, связывающих высоту глаза наблюдателя е и высоту ориентира h при коэффициенте рефракции  (рис.1.42):

(1.126)

где Д_е и Д_h  соответственно дальности видимого горизонта с высоты глаза наблюдателя и высоты предмета. Т.о. дальность видимости предмета, рассчитанная по высоте глаза наблюдателя и высоте предмета называется географической или геометрической дальностью видимости.

Расчёт географической дальности видимости предмета может производиться по табл. 2.3 МТ – 2000 по аргументам e и h или по табл. 2.1 МТ – 2000 суммированием результатов, полученных двукратным входом в таблицу по аргументам е и h. Можно также получить Д_п по номограмме Струйского, которая приведена в МТ – 2000 под номером 2.4, а также в каждой книге “Огни” и “Огни и знаки” (рис.1.43).

На морских навигационных картах и в навигационных пособиях географическая дальность видимости ориентиров даётся для постоянной высоты глаза наблюдателя е = 5 м и обозначается как Д_к - дальность видимости указанная на карте.

Подставив значение е = 5 м в формулу (1.126), получим:

(1.127)

Для определения Д_п надо к Д_к ввести поправку Д, величина которой и знак определяются формулой:

(1.128)

Если фактическая высота глаза больше 5 м, то Д имеет знак “+”, если меньше - знак ““. Таким образом:

. (1.129)

Величина Д_п зависит также и от остроты зрения, которая выражается в разрешающей способности глаза по углу, т.е. определяется и наименьшим углом, на котором предмет и линия горизонта различаются раздельно (рис.1.44).

В соответствии с формулой (1.126)

Н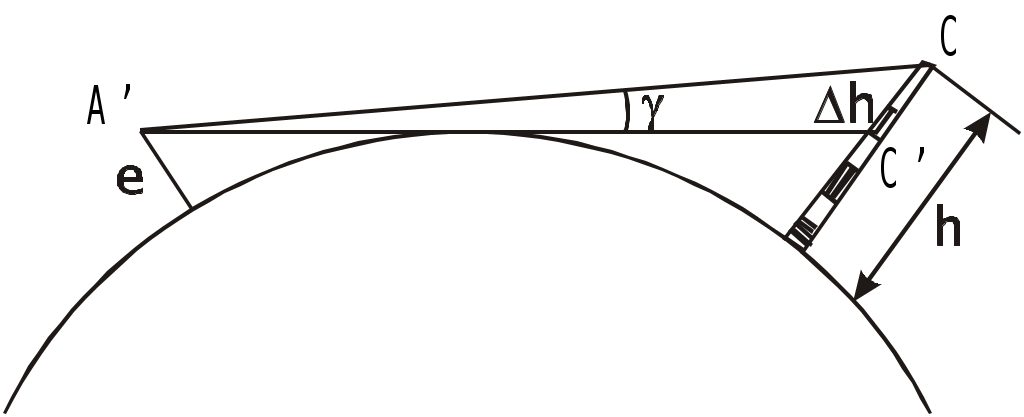
Рис. 1.44. Дальность видимости предметов с учетом разрешающей способности глаза
о из-за разрешающей способности глаза  наблюдатель увидит предмет только тогда, когда его угловые размеры будут не меньше , т.е. когда он будет виден над линией горизонта не менее чем на h, которая из элементарного АСС при углах С и С близких к 90 будет h = Д_п .

Чтобы получить Д_п^ в милях при h в метрах: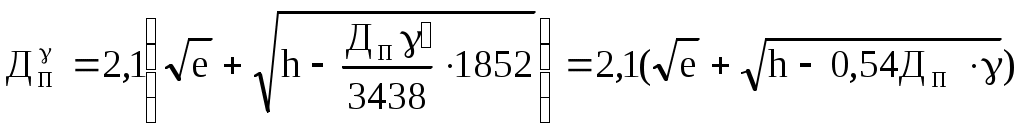

, (1.130)

где Д_п^ - географическая дальность видимости предмета с учётом разрешающей способности глаза.

Практическими наблюдениями определено, что при открытии маяка  =2, а при скрытии  =1,5.