Вся навигация. вся навигация 1. Фигура и модели Земли

• Название: Фигура и модели Земли
• Анкор: Вся навигация
• Дата: 31.01.2023
• Размер: 3.45 Mb.
• Имя файла: вся навигация 1.doc
• Тип: Документы; #913997
• страница: 8 из 9

Пример. Найти географическую дальность видимости маяка высотой h=39 м, если высота глаза наблюдателя е=9 м, без учёта и с учётом разрешающей способности глаза  =1,5.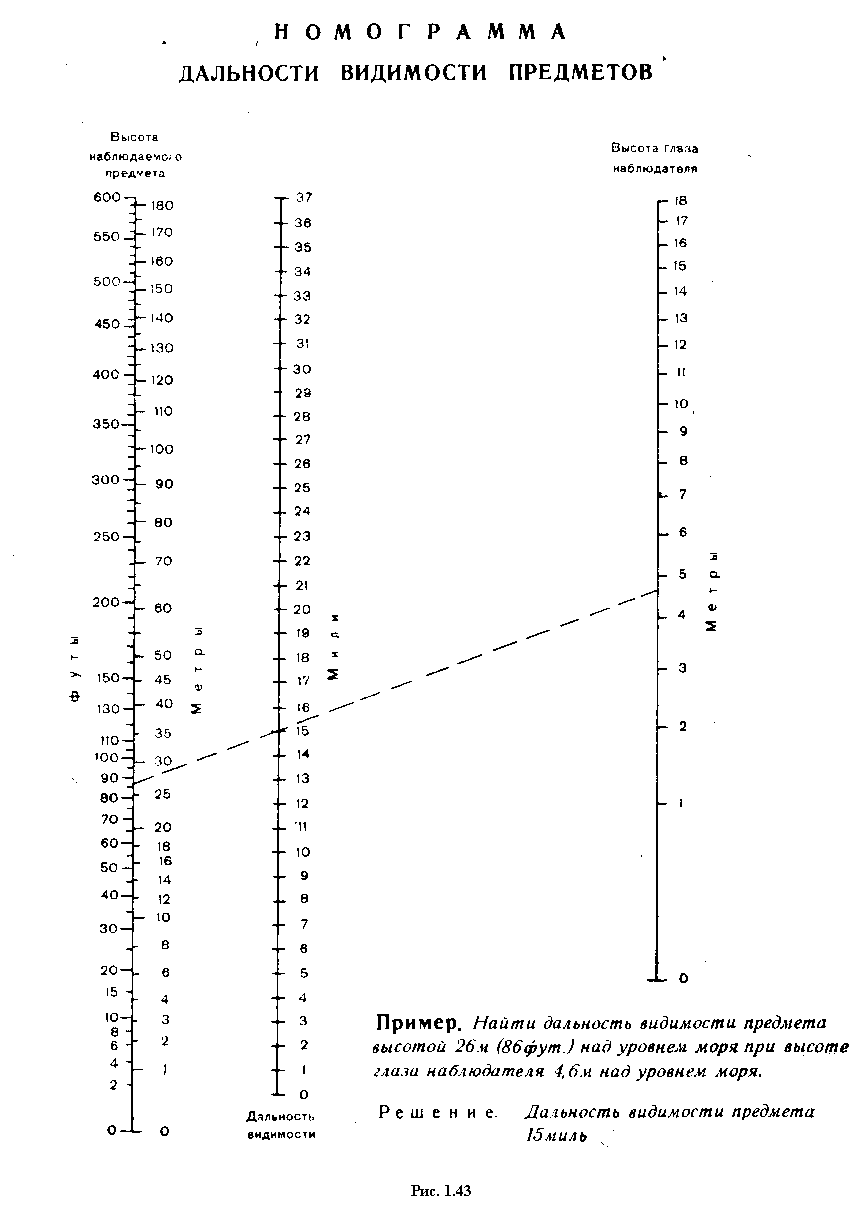







Влияние гидрометеорологических факторов на дальность видимости огней

На дальность видимости ориентиров кроме геометрических факторов (е и h) влияет также контрастность, позволяющая выделить ориентир на окружающем фоне.

Дальность видимости ориентиров днём, учитывающая также контрастность, называется дневной оптической дальностью видимости.

Для обеспечения безопасного судовождения в ночных условиях используются специальные средства навигационного оборудования, имеющие светооптические приборы: маяки, светящиеся навигационные знаки и навигационные огни.

Морской маяк - это специальное капитальное сооружение с дальностью видимости белого или приведённых к нему цветных огней не менее 10 миль.

Светящийся морской навигационный знак - капитальное сооружение, имеющее светооптический аппарат с дальностью видимости белого или приведённых к нему цветных огней менее 10 миль.

Морской навигационный огонь - световой прибор, установленный на естественных объектах или сооружениях неспециальной постройки. Такие СНО часто действуют автоматически.

В тёмное время суток дальность видимости огней маяков и светящихся навигационных знаков зависит не только от высоты глаза наблюдателя и высоты светящегося СНО, но и от силы источника света, цвета огня, конструкции светооптического аппарата, а также и от прозрачности атмосферы.

Дальность видимости, учитывающая все эти факторы, называется ночной оптической дальностью видимости, т.е. это максимальная дальность видимости огня в данное время при данной метеорологической дальности видимости.

Метеорологическая дальность видимости зависит от прозрачности атмосферы. Часть светового потока огней светящих СНО поглощается частицами, содержащимися в воздухе, поэтому происходит ослабление силы света, характеризующееся коэффициентом прозрачности атмосферы :

(1.131)

где I₀ - сила света источника; I₁ - сила света на некотором расстоянии от источника, принимаемого за единицу (1 км, 1 миля).

Коэффициент прозрачности атмосферы всегда меньше единицы, поэтому географическая дальность видимости обычно больше реальной, за исключением аномальных случаев.

Прозрачность атмосферы в баллах оценивается по шкале видимости таблицы 5.20 МТ – 2000 в зависимости от состояния атмосферы: дождь, туман, снег, дымка и т.д.

Так как оптическая дальность видимости огней изменяется в значительных пределах в зависимости от прозрачности атмосферы, Международная ассоциация маячных служб (МАМС) рекомендовала использовать термин “номинальная дальность видимости”.

Номинальной дальностью видимости огня называется оптическая дальность видимости при, метеорологической дальности видимости 10 миль, что соответствует коэффициенту прозрачности атмосферы  = 0,74. Номинальная дальность видимости указывается в навигационных пособиях многих зарубежных стран. На отечественных картах и в руководствах для плавания указывается стандартная дальность видимости (если она меньше географической дальности видимости).

Стандартной дальностью видимости огня называется оптическая дальность видимости при метеорологической дальности видимости 13,5 миль, что соответствует коэффициенту прозрачности атмосферы  = 0,8.

В навигационных пособиях “Огни”, “Огни и знаки” кроме таблицы дальности видимого горизонта и номограммы дальности видимости предметов есть и номограмма оптической дальности видимости огней (рис.1.45). Эта же номограмма приведена в МТ – 2000 под номером 2.5.

Аргументами для входа в номограмму являются сила света, или номинальная, или стандартная дальности видимости, (полученные из навигационных пособий), и метеорологическая дальность видимости, (полученная из метеорологического прогноза). По этим аргументам из номограммы получают оптическую дальность видимости.

При проектировании маяков и огней стремятся, чтобы оптическая дальность видимости была бы равна географической дальности видимости при ясной погоде. Однако, для многих огней оптическая дальность видимости меньше географической. Если эти дальности не равны, то на картах и в руководствах для плавания указывается меньшая из них.

Для практических расчётов ожидаемой дальности видимости огня днём надо по высотам глаза наблюдателя и ориентира рассчитать Д_п по формуле (1.126). Ночью: а) если оптическая дальность видимости больше географической, надо взять поправку за высоту глаза наблюдателя и рассчитать географическую дальность видимости по формулам (1.128) и (1.129). Принять меньшую из оптической и географической, рассчитанной по этим формулам; б) если оптическая дальность видимости меньше географической - принять оптическую дальность.

Если на карте у огня или маяка Д_к  2,1 h + 4,7 , то поправку Д вводить не нужно, т.к. эта дальность видимости оптическая меньшая географической дальности видимости.

Пример. Высота глаза наблюдателя e = 11 м, дальность видимости огня, указанная на карте Д_к =16 миль. Номинальная дальность видимости маяка из навигационного пособия “Огни” 14 миль. Метеорологическая дальность видимости 17 миль. На каком расстоянии можно ожидать открытия огня маяка?

Решение:

По номограмме Допт  19,5 мили.

п о е = 11м  Д_е = 6,9 мили

Д₅ = 4,7 мили

Д =+2,2 мили

Д_к = 16,0 мили

Д_п = 18,2 мили

Ответ: можно ожидать открытия огня с расстояния 18,2 мили.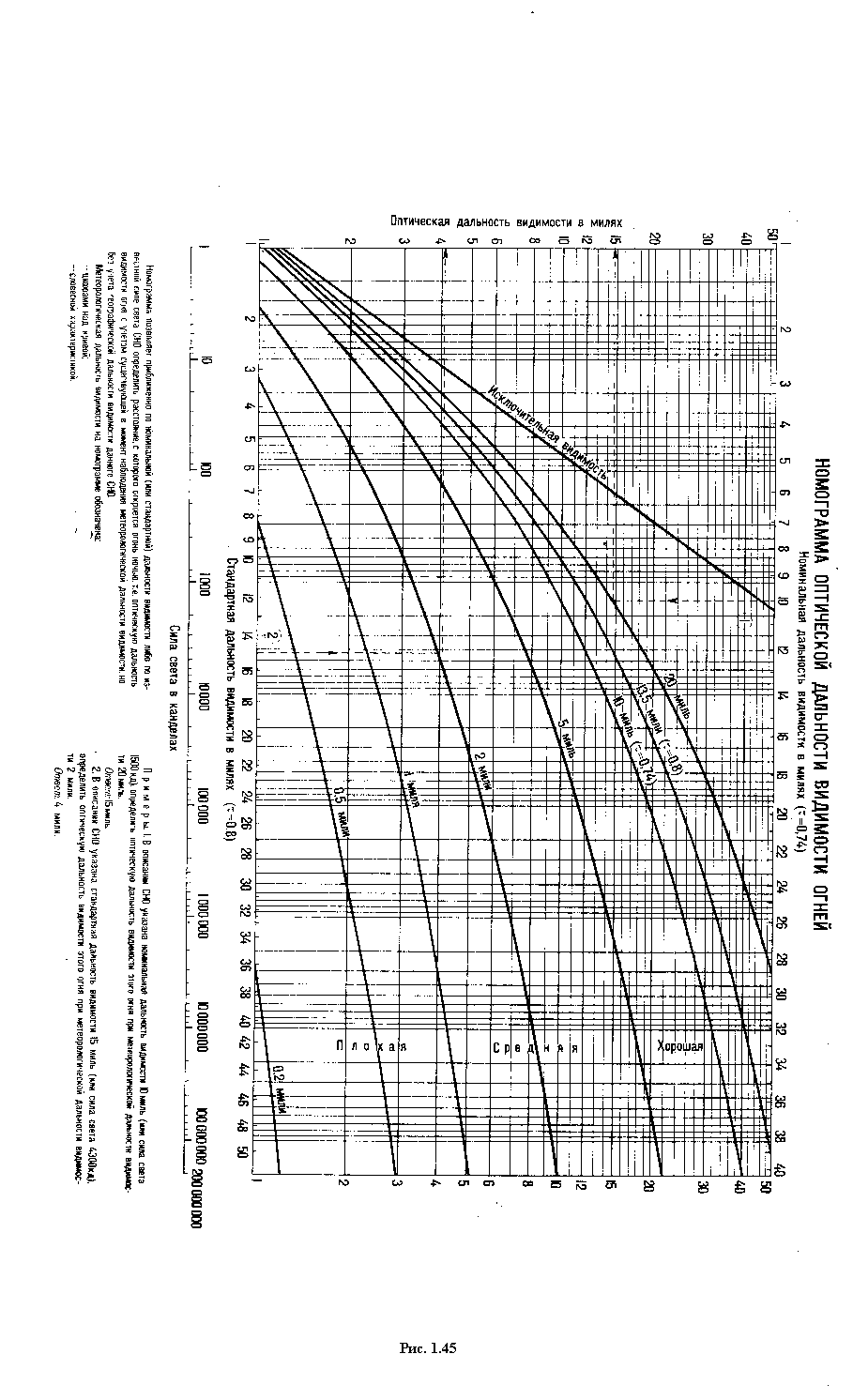



Морские карты. Картографические проекции. Поперечная равноугольная цилиндрическая проекция Гаусса и её использование в судовождении. Перспективные проекции: стереографическая, гномоническая.
Карта – уменьшенное искажённое изображение сферической поверхности Земли на плоскости, при условии, что искажения закономерны.

План – не искажённое за счёт малости изображаемого участка изображение земной поверхности на плоскости.

Картографическая сетка – совокупность линий, изображающих на карте меридианы и параллели.

Картографическая проекция – математически обоснованный способ изображения меридианов и параллелей.

Географическая карта - построенное в данной проекции условное изображение всей земной поверхности или её части.

Карты бывают различными по назначению и масштабу, например: планисферы – изображающие всю Землю или полушарие, генеральные или общие – изображающие отдельные страны, океаны и моря, частные – изображающие меньшие пространства, топографические – изображающие подробности поверхности суши, орографические – карты рельефа, геологичекие – залегание пластов и т.д.

Морские карты – специальные географические карты, предназначенные в основном для обеспечения судовождения. В общей классификации географических карт они отнесены к техническим. Особое место среди морских карт занимают МНК, служащие для прокладки курса судна и определения его места в море. В судовой коллекции также могут быть вспомогательные и справочные карты.

Классификация картографических проекций.
По характеру искажений все картографические проекции делят на:

• 
  Равноугольные или конформные – проекции, в которых фигуры на картах подобны соответствующим фигурам на поверхности Земли, но их площади не пропорциональны. Углы между объектами на местности соответствуют таковым на карте.
  
• 
  Равновеликие или эквивалентные – у которых сохранена пропорциональность площадей фигур, но при этом искажаются углы между объектами.
  
• 
  Равнопромежуточные – сохраняющие длину по одному из главных направлений эллипса искажений, т.е., например, круг на местности на карте изображается в виде эллипса, у которого одна из полуосей равна радиусу такого круга.
  
• 
  Произвольные – все остальные, не обладающие вышеуказанными свойствами, но подчиняющиеся иным условиям.
  

По способу построения проекции делят на:

• 
  П
  F
  ерспективные – изображение получается в пересечении картинной плоскости с прямой, соединяющей проецируемую точку с точкой зрения. Картинная плоскость и точка зрения могут занимать различные положения по отношению к поверхности Земли: рисунки если картинная плоскость касается поверхности Земли в какой-либо точке, то проекция называется азимутальной. Азимутальные проекции делятся на: стереографические – когда точка зрения находится на противоположном полюсе сферы , ортографические – когда точка зрения удалена в бесконечность, внешние – точка зрения находится на конечном расстоянии далее противоположного полюса сферы , центральные или гномонические – когда точка зрения находится в центре сферы. Перспективные проекции – не конформны и не эквивалентны. Измерение расстояний на картах, построенных в таких проекциях затруднено, зато дуга большого круга изображается прямой линией, что удобно при прокладке радиопеленгов, а также - курсов при плавании по ДБК. Примеры. В этой проекции могут строиться также карты приполярных областей.
  

В зависимости от точки касания картинной плоскости гномонические проекции делятся на: нормальные или полярные – касание на одном из полюсов поперечные или экваториальные – касание – на экваторе горизонтальные или косые – касание в любой точке между полюсом и экватором (меридианы на карте в такой проекции представляют собой расходящиеся от полюса лучи, а параллели – эллипсы, гиперболы или параболы.

• 
  Цилиндрические – поверхность Земли проецируется на поверхность цилиндра, касающегося земного сфероида с последующим разворотом цилиндра в плоскость. Делятся на нормальные, когда ось цилиндра параллельна оси Земли (Меркаторская проекция), поперечные, когда ось цилиндра перпендикулярна земной оси (проекция Гаусса) и косые, когда земная ось занимает промежуточное положение по отношению к оси цилиндра. Рисунки.
  

Цилиндрическую проекцию можно представить, как проекцию шара на касательный к экватору или секущий по 2 малым кругам поверхность цилиндр с последующим разворотом в плоскость.

точка м определяет равновеликую проекцию, - равноугольную (Меркаторскую), - произвольну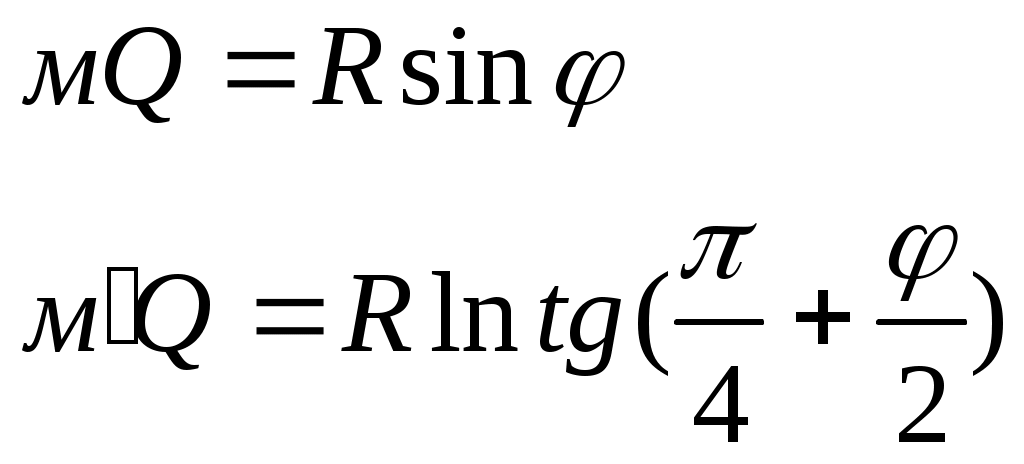ю.

• 
  Конические – поверхность Земли проецируется на конус, касающийся земного сфероида.
  
• 
  Условные – построенные более сложными геометрическими приёмами.
  

В судовождении применяются цилиндрические (Меркаторская, Гаусса) и азимутальные проекции.

Проекция Гаусса и её особенности.
В этой проекции составляются речные карты. Она является равноугольной поперечной цилиндрической. Земля делится по меридианам на части (зоны) по 6° каждая. Средний меридиан в каждой зоне называется осевым меридианом. Он делит зону на восточную и западную части. Счёт зон ведётся от Гринвичского меридиана с запада на восток. Каждая зона последовательно проектируется на поверхность цилиндра, который касается земного шара по линии осевого меридиана. Если такой цилиндр разрезать, то получится плоское изображение поверхности Земли в виде отдельных зон. Осевой меридиан и экватор в каждой зоне изображаются прямыми, взаимно перпендикулярными линиями. Они изображаются без искажения длины.


Остальные параллели и меридианы изображаются кривыми и искажаются, причём, более всего – у краёв зоны (до 0.001 длины линии, измеренной на карте).



Такие искажения при практической работе неощутимы, поэтому, масштаб любого участка карты считается постоянным (на сравнительно небольших участках рек и водохранилищ – несколько сантиметров на 1 километр). Курс изображается прямой линией. Осевой меридиан принимается за ось Х, экватор – за ось У, следовательно, вся проекция строится в системе прямоугольных плоских координат. В зонах наносится координатная сетка, линии которой отстоят друг от друга на целое число километров, поэтому она называется километровой. Зона делится на листы карт. Все направления на картах – от вертикальных линий сетки. Угол между северной частью вертикальной линии координатной сетки и носовой частью ДП судна называется дирекционным курсом и обозначается Т. Угол между северной частью вертикальной линии координатной сетки и направлением на пеленгуемый объект называется дирекционным углом и обозначается α. Угол между ИМ данной точки и вертикальной линией координатной сетки называется углом схождения меридианов и обозначается γ.


где - долгота места.

- долгота осевого меридиана.

φ – широта места.

Угол между магнитным меридианом и вертикальной линией называется ориентирным углом и обозначается Δ.


Сведения о величине и знаке ориентирного угла Δ, магнитного склонения d и γ помещены в виде схемы на полях карты водохранилища.

Формулы для решения задач на исправление и перевод направлений в проекции Гаусса: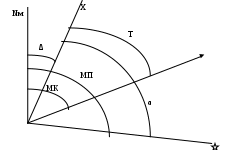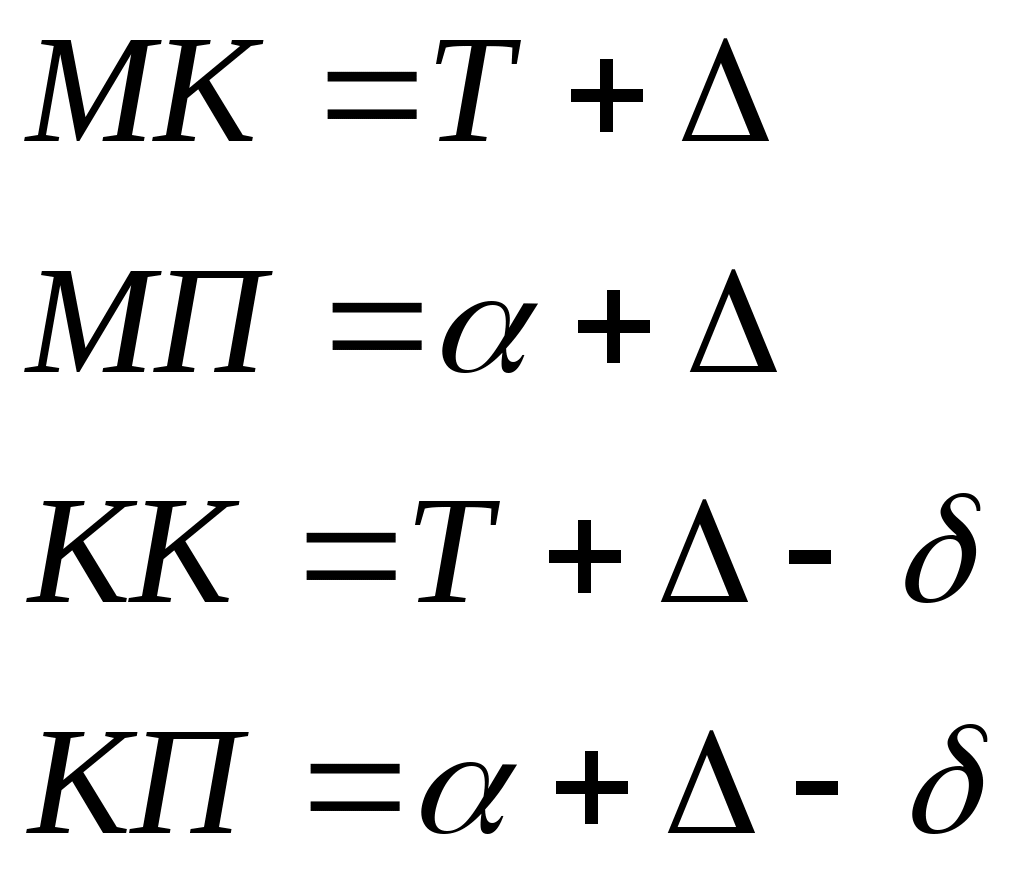







Требования к МНК. Меридиональная часть. Локсодромия и анализ её уравнения. Теория и свойства Меркаторской проекции. Масштаб карты, единица карты. Построение карты. Классификация морских карт. Оценка достоинства МНК.
Элементарная теория Меркаторской карты: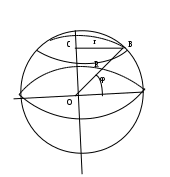



Из треугольника ОВС:

т.е. при проектировании сфероида на цилиндр происходит растяжение каждой параллели пропорционально секансу её широты, отсюда, чтобы сохранить на карте подобие очертаний предметов (равноугольность), необходимо вытянуть на столько же и меридианы.

Требования к МНК:

• 
  Путь судна, идущего постоянным курсом, т.е., пересекающего все меридианы под определённым углом, должен изображаться прямой.
  
• 
  Углы, измеряемые на местности (курс, пеленг), должны быть равны соответствующим углам на карте.
  
• 
  Если курс равен 0 или 180°, то он совпадает с меридианом, следовательно, и меридиан должен изображаться прямой, параллельной такому курсу. По той же причине экватор и параллели должны изображаться прямыми, параллельными между собой.
  

Локсодромия («косой бег»).

Если судно совершает переход одним и тем же курсом, то его путь на поверхности Земли изображается линией двоякой кривизны – локсодромией. Она представляет из себя логарифмическую спираль и пересекает все меридианы под одним и тем же углом, стремясь к полюсу, но никогда его не достигая (при условии, что курс не равен 0 или 180°). На меркаторской карте локсодромия изображается прямой, которая не выражает кратчайшего расстояния между 2 точками на земной поверхности. Уравнение локсодромии необходимо для получения точного выражения МЧ.
По Сакеллари:



Считая Землю сферой, выберем на ней 2 меридиана с разностью долгот Δλ. На этих меридианах отложим 2 точки и с бесконечно малой разностью широт Δφ. Проведя через т. параллель, получим прямоугольный треугольник . Из треугольника радиус этой параллели: . Из этого выражения следует, что длина любой параллели равна длине экватора, умноженной на cosφ ( ).

Для отрезков параллели и экватора соблюдается то же соотношение:



Поскольку треугольник элементарно мал, его можно считать плоским, тогда: , откуда:





переходя к дифференциалам, получим:

По учебнику:



Элемент локсодромии 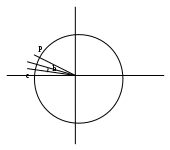настолько мал, что треугольник можно принять за плоский. Угол представляет из себя курс судна.

- разность долгот точек и , радиан.



(3)

для в функции т.А:



При разбиении дуги меридиана на столь малые части, чтобы принять, что каждая из них вся лежит в одной широте:



ep – расстояние на меркаторской проекции по меридиану от экватора до параллели называется меридиональной частью этой параллели. Таким образом на карте минуты растянуты и расстояние от экватора, выраженное в экваториальных милях, будет больше, чем число минут в дуге меридиана до той же параллели. В таблицах МТ-75 меридиональные части даны в экваториальных минутах.

Меридиональная разность широт – меридиональные части из МТ-75 – разность, экваториальные мили.

М.Ч. для параллели 60°30'=4587,8

59°30'=4467,8

Меридиональная РШ 120 экваториальных миль.

Меркаторская миля в широте 60°:

экваториальных мили.

Если проделать те же расчёты для широты 30°, получим , т.е., меркаторская миля в широте 60° по карте в 1.72 раза больше, чем в широте 30°. Отсюда – для измерения расстояний на меркаторской карте необходимо пользоваться линейным масштабом, взятым в той же широте, где лежит измеряемое расстояние.