Расчётно-графическая работа на тему: Определение активности компонентов металлургических расплавов. Расчётно графическая работа № 2. Физическая химия металлургических процессов
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Магнитогорский государственный технический университет им. Г.И. Носова» Кафедра физической химии и химической технологии Определение активности компонентов металлургических расплавовРасчётно-графическая работа по дисциплине «Физическая химия металлургических процессов» Выполнил: Студент группы ММб-19-1 Иванов Д.О. Проверил: Старший преподаватель кафедры Металлургии и химических технологий С.В.Юдина Магнитогорск 2021 1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1. Общие определения Раствором называют однородную смесь, состоящую из двух или более компонентов, состав которой может непрерывно меняться в некоторых пределах (фаза переменного состава). С термодинамической точки зрения все составляющие раствора равноценны. Деление их на растворитель и растворенное вещество является условным. Обычно растворителем называют преобладающий в количественном соотношении компонент, добавление которого не приводит к образованию гетерогенной системы. Если один из компонентов при данных условиях находится в жидком агрегатном состоянии, а другие в твердом или газообразном, то растворителем принято считать жидкость даже в том случае, если остальные вещества присутствуют в большем количестве. Молем раствора называют такое его количество, при котором сумма мольных долей каждого компонента равна единице. 1.2. Химический потенциал, активность Основным вопросом термодинамики растворов является установление зависимости равновесных свойств растворов от состава и свойств его компонентов, в частности, определение способности компонентов раствора реагировать с другими веществами. Если реагирующие вещества находятся не в чистом виде, а в растворенном состоянии, то их способность к взаимодействию зависит и от их концентрации в растворе. Существует несколько способов определения состава раствора, т.е. способов выражения концентрации. Общепринятыми являются: мольная (молярная) доля i - го компонента – хi (атомный процент), массовая доля – wi (массовый процент [%]), молярность – сi, моляльность – mi. В очень разбавленных растворах концентрации компонентов, выраженные в различных единицах, пропорциональны друг другу, но при увеличении концентрации компонентов прямая пропорциональность нарушается. Свойства растворов характеризуются термодинамическими функциями, например: энтальпией – Н, энтропией - S, энергией Гиббса – G. Эти свойства являются экстенсивными и относятся ко всему раствору как целому. Если обозначить какое – либо экстенсивное свойство раствора через Z, то для оценки изменения этого экстенсивного свойства при изменении лишь одного компонента (ni ) при условии, что количество всех других компонентов ( j n ), а также давление и 4 температура, остаются неизменными. Льюисом была введена парциальная мольная величина  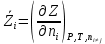 (1) (1)Эта величина - Zi , отображает вклад данного компонента в общее свойство раствора и позволяет выразить зависимость равновесных свойств раствора от состава и свойств компонентов его составляющих. Например, в случае бинарного раствора, зависимость общего свойства Z одного моля раствора, будет иметь вид Z= 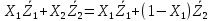 (2) (2)Среди парциальных мольных величин особое значение имеет парциальная мольная энергия Гиббса ( Gi ), которая соответствует химическому потенциалу компонента - i1: 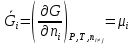 ( (3) ( (3)Если рассматриваемая система многофазна (например, поликомпонентный шлак или сплав на основе железа), то равенство химических потенциалов данного компонента в каждой сосуществующей фазе является условием химического равновесия. Поскольку химический потенциал не является непосредственно измеряемой величиной, то на практике используют соотношения, где химический потенциал выражен через экспериментально определяемые значения, например, парциальные давления или концентрации. Выражение для химического потенциала i- го компонента в идеальном растворе газов 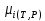 - имеет вид: - имеет вид: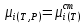 +RT +RT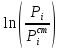 (4) (4)где 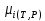 - химический потенциал чистого i-го компонента при температуре Т и стандартном давлении - химический потенциал чистого i-го компонента при температуре Т и стандартном давлении 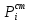 (зависит только от 1 Химический потенциал может быть найден как частная производная характеристической функции (зависит только от 1 Химический потенциал может быть найден как частная производная характеристической функции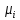 = =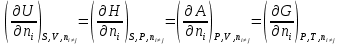 ,но только последнее выражение дает явную зависимость рассматриваемой функции состояния от числа молей. 5 температуры), а Рi – парциальное давление i- го компонента в идеальном растворе газов при той же температуре. Если в качестве стандартного состояния при данной температуре выбрано состояние, в котором 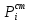 =1 атм., то уравнение (4) будет иметь вид: =1 атм., то уравнение (4) будет иметь вид: 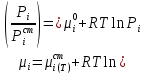 (5) (5) здесь Pi - безразмерная величина, численно совпадающая с давлением газа в атмосферах. Для того чтобы сделать возможным применение законов идеальных растворов к реальным системам, вместо концентрации растворенных веществ используют значения их активности в растворе. В качестве определения активности компонента раствора используется, как тождество, следующее соотношение: 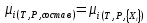 = =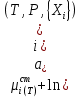 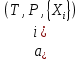 - активность i - го компонента; - активность i - го компонента; 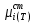 - химический потенциал этого компонента в состоянии, принимаемом за стандартное. Активность - химический потенциал этого компонента в состоянии, принимаемом за стандартное. Активность 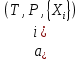 - сложная функция температуры, давления и состава раствора. Для систем, рассматриваемых при постоянном давлении и температуре, достаточно учесть ее зависимость от состава раствора. Функцию - сложная функция температуры, давления и состава раствора. Для систем, рассматриваемых при постоянном давлении и температуре, достаточно учесть ее зависимость от состава раствора. Функцию 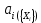 - обычно записывают в виде произведения концентрации на коэффициент активности ai iXi , который и выражает суммарно степень отклонения раствора от идеальности - обычно записывают в виде произведения концентрации на коэффициент активности ai iXi , который и выражает суммарно степень отклонения раствора от идеальности 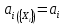 - мольный коэффициент активности, - мольный коэффициент активности, 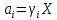 - - молярный коэффициент активности, ( - - молярный коэффициент активности, (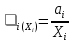 - моляльный коэффициент активности, - моляльный коэффициент активности,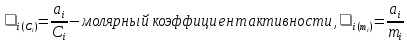 ). Поскольку для фаз, находящихся в термодинамическом равновесии (например, газовая – (г) и конденсированная – (к)) должно выполняться равенство: ). Поскольку для фаз, находящихся в термодинамическом равновесии (например, газовая – (г) и конденсированная – (к)) должно выполняться равенство: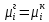 = , и, следовательно = , и, следовательно 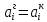 , (7) , (7)при условии, что к i г ai и a отнесены к одному и тому же стандартному состоянию, то из уравнений (4), (6) и (7) следует, что активность i - го компонента в растворе определяется соотношением: 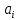 = = 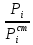 (8) (8)(8) В стандартном состоянии ст i i и активность ai = 1. Для разных типов растворов наиболее удобны следующие стандартные состояния. 1.3. Выбор стандартного состояния, типы (модели) растворов В качестве стандартного состояния может быть выбрано любое состояние раствора или компонентов, входящих в состав раствора. Выбор стандартного состояния определяется удобством нахождения для этого состояния давления насыщенного пара или другой термодинамической величины и зависит от области концентраций, для которой определяется активность компонента в растворе. На практике наибольшее распространение получили следующие способы выбора стандартных состояний. 1. В качестве стандартного состояния выбираются чистые компоненты при температуре раствора. В этом случае все компоненты являются как бы равноправными, и такой способ выбора стандартного состояния называют симметричной системой сравнения. 2. В качестве стандартного состояния выбирается бесконечно – разбавленный раствор. В этом случае компоненты в растворе как бы не равноправны, и такой способ выбора стандартного состояния называют несимметричной системой сравнения 3.Состояние вещества в растворе, отвечающее 1% - ной массовой концентрации компонента. В первом случае, когда в качестве стандартного состояния выбирают чистое вещество, активность характеризует степень отклонения от закона Рауля. Если использовать индекс “R” в обозначении свойств, относящихся к растворам подчиняющимся закону Рауля, то в случае бинарного раствора «А – В» активность и коэффициент активности компонента “В” запишутся, соответственно, в виде: 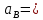 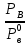 , , 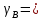 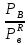 и и 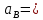 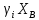 (9) (9)где РВ – давление насыщенного пара компонента В над раствором с определенной концентрацией В (рис. 1, например ХВ); 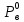 - давление насыщенного компонента В над чистым веществом В при той же температуре; - давление насыщенного компонента В над чистым веществом В при той же температуре; 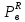 - давление насыщенного пара компонента В, рассчитанное по закону Рауля. При таком выборе стандартного состояния i = 1 при Xi = 1. - давление насыщенного пара компонента В, рассчитанное по закону Рауля. При таком выборе стандартного состояния i = 1 при Xi = 1. В случае отрицательных отклонений от закона Рауля 7 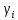 < 1 (случай, показанный на рис. 1), для положительных отклонений от закона Рауля < 1 (случай, показанный на рис. 1), для положительных отклонений от закона Рауля 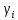 > 1. Обычно первый способ выбора стандартного состояния более удобен, когда компоненты смешиваются друг с другом во всем интервале концентраций. Применительно к растворам различных компонентов в металлах, когда речь идет, как правило, о разбавленных растворах этих компонентов, используют второй способ выбора стандартного состояния. > 1. Обычно первый способ выбора стандартного состояния более удобен, когда компоненты смешиваются друг с другом во всем интервале концентраций. Применительно к растворам различных компонентов в металлах, когда речь идет, как правило, о разбавленных растворах этих компонентов, используют второй способ выбора стандартного состояния. Состояние растворителя (металла) в бесконечно разбавленном растворе практически не отличается от состояния растворителя, взятого в чистом виде, тогда как состояние растворенных веществ сильно отличается от того, какое эти вещества имели бы в чистом виде. В таких разбавленных растворах термодинамические характеристики растворенного вещества пропорциональны его концентрации, несмотря на значительные отклонения от закона Рауля (рис.1). Такое поведение растворенного вещества в разбавленном растворе соответствует закону Генри 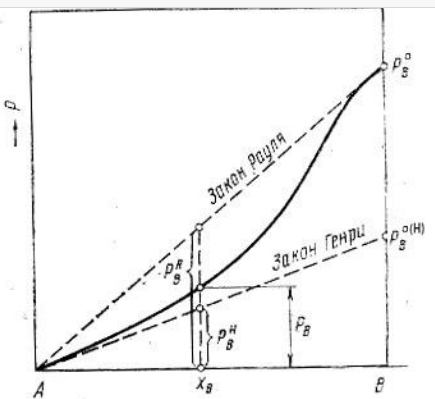 Рис.1. Давление насыщенного пара компонента В в бинарном растворе А-В ( PB ) и отклонение величины PB от значения, рассчитанного по закону Рауля ( 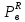 ) и Генри ( ) и Генри (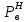 ) )(для таких компонентов будем использовать индекс “H”). Гипотетическое стандартное состояние вещества (Генриево гипотетическое состояние) получают экстраполяцией закона Генри от крайне низких концентраций 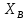 →0 до значения →0 до значения 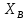 →1. →1. Это состояние (точка 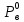 на рис. 1) представляет собой чистое вещество В в гипотетическом, нереальном состоянии, в котором оно существовало бы как чистый компонент, если бы подчинялось закону Генри во всем интервале концентраций, вплоть до чистого вещества. на рис. 1) представляет собой чистое вещество В в гипотетическом, нереальном состоянии, в котором оно существовало бы как чистый компонент, если бы подчинялось закону Генри во всем интервале концентраций, вплоть до чистого вещества. Иными словами, если бы вещество в чистом виде характеризовалось теми же свойствами, что и в бесконечно разбавленном растворе. Активность и коэффициент активности компонента 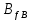 запишутся, соответственно, в виде: запишутся, соответственно, в виде: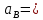 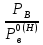 , , 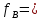 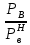 и и 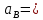 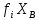 ( (10) ( (10)где 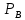 – давление насыщенного пара компонента В над раствором с определенной концентрацией В (рис. 1, например – давление насыщенного пара компонента В над раствором с определенной концентрацией В (рис. 1, например 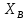 ); ); 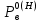 - давление насыщенного компонента В в Генриевом гипотетическом состоянии при той же температуре, а - давление насыщенного компонента В в Генриевом гипотетическом состоянии при той же температуре, а 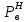 давление насыщенного пара компонента В, рассчитанное по закону Генри. давление насыщенного пара компонента В, рассчитанное по закону Генри. Использование для обозначения коэффициента активности веществ в разбавленных растворах символа 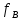 введено для того, чтобы отличить этот коэффициент активности, показывающий отклонение от закона Генри от коэффициента активности введено для того, чтобы отличить этот коэффициент активности, показывающий отклонение от закона Генри от коэффициента активности 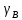 , показывающего отклонение от закона Рауля. , показывающего отклонение от закона Рауля. Для растворенных веществ при данном выборе стандартного состояния принимается, что 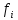 → 1 при Xi → 0. . В случае отрицательных отклонений от закона Генри → 1 при Xi → 0. . В случае отрицательных отклонений от закона Генри 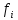 < 1, для положительных отклонений от закона Генри < 1, для положительных отклонений от закона Генри 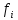 > 1 (случай, показанный на рис. 1). > 1 (случай, показанный на рис. 1). Данный (второй) способ выбора стандартного состояния более удобен в тех случаях, когда растворимость ограничена. Третий способ выбора стандартного состояния – отвечающий 1% - ной массовой концентрации компонента, широко используется в практических расчетах металлургических процессов с участием разбавленных растворов. Поскольку в очень разбавленных растворах концентрации компонентов, выраженные в различных единицах, пропорциональны друг другу, то это устраняет необходимость перевода процентов по массе, которыми обычно выражают состав растворов, в молярные доли. Активность растворенного компонента “В” по отношению к 1% - ному стандартному состоянию ( aB(1%) ) запишется в виде: 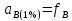 [B %] , (11) [B %] , (11) где 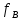 - коэффициент активности для этого стандартного состояния. Значение коэффициента активности - коэффициент активности для этого стандартного состояния. Значение коэффициента активности 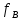 равно коэффициенту активности для Генриевого гипотетического состояния, поскольку оба они характеризуют отклонение действительного поведения растворенного вещества В в растворе от его идеального поведения в бесконечно 9 разбавленном растворе, т.е. от закона Генри (рис. 2). равно коэффициенту активности для Генриевого гипотетического состояния, поскольку оба они характеризуют отклонение действительного поведения растворенного вещества В в растворе от его идеального поведения в бесконечно 9 разбавленном растворе, т.е. от закона Генри (рис. 2). Если коэффициент активности 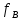 остается равным единице при увеличении концентрации до 1 %, то активность остается равным единице при увеличении концентрации до 1 %, то активность 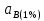 будет равна единице при концентрации компонента В, равной 1% по массе. Такой (реальный) 1% - ный раствор будет стандартным состоянием для рассматриваемого случая. Если же коэффициент активности будет равна единице при концентрации компонента В, равной 1% по массе. Такой (реальный) 1% - ный раствор будет стандартным состоянием для рассматриваемого случая. Если же коэффициент активности 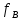 отклоняется от единицы уже при концентрациях ниже 1 % (рис. 2), то стандартным состоянием для такого случая будет гипотетический 1 % - ный раствор с таким же коэффициентом активности, как при бесконечном разбавлении. отклоняется от единицы уже при концентрациях ниже 1 % (рис. 2), то стандартным состоянием для такого случая будет гипотетический 1 % - ный раствор с таким же коэффициентом активности, как при бесконечном разбавлении. 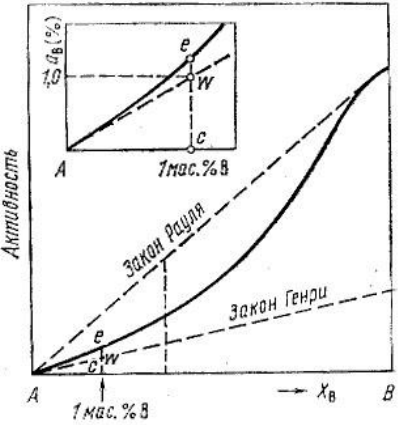 Рис.2. Активность компонента В в бинарном растворе А – В и ее отклонение от идеального поведения Модель «идеальный раствор» (раствор, в котором выполняется закон Рауля для любого компонента) предусматривает энергетическую неразличимость частиц, составляющих раствор: ΔE12 = ΔE11 = ΔE22 (12) В уравнении (12) Е – потенциальная энергия взаимодействия частиц, а индексы 1 и 2 означают компоненты раствора. Поскольку потенциальная энергия Е определяется электронным строением, условие (12) соблюдается весьма редко; это изомеров и изотопов. В реальных растворах возникают отклонения от закона Рауля. Различают три типа таких отклонений: отрицательные, положительные и знакопеременные. Отрицательные отклонения возникают в растворах, где разнородные взаимодействия (Eij) значительно сильнее однородных (Eii): E12 > 0,5 (E11 + E22) (13) В таких системах, как правило, образуются химические соединения, и раствор образуется с выделением теплоты (∆Нсмеш< 0) и уменьшением 10 объема (∆Vсмеш< 0). Отрицательные отклонения характерны для систем: вода - минеральные кислоты, железо - кремний, СаО-Al2O3, SiO2-Al2O3. В них активность компонентов меньше мольной доли. Положительные отклонения возникают в системах, где разнородные взаимодействия значительно слабее однородных: E12 < 0,5 (E11 + E22) (14) В таких системах, когда различия в однородных взаимодействиях значительно часто имеет место расслоение раствора на две фазы (ограниченная растворимость в жидком состоянии). Примером таких систем являются: вода-фенол, железо-медь, железо-свинец, железосеребро. Такие смеси образуются с поглощением теплоты, а активности компонентов больше их мольной доли. 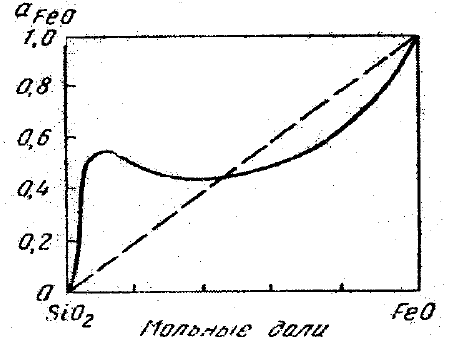 Рис. 3. Активность FeO в расплавах системы FeO – SiO2 при 16000С 1.4. Определение активности компонентов в шлаковых расплавах и многокомпонентных сплавах на основе железа Шлаки – это оксидные системы. В расплавленном состоянии они находятся в контакте с металлическими сплавами в ходе технологического процесса и играют большую роль в процессах получения металлов, в литейном производстве. Главными компонентами шлаков являются оксиды металлов. Активности компонентов шлака определяют, исходя из различных моделей. Простейшая модель используется в молекулярной теории шлаков. Согласно этой теории жидкий шлак состоит из молекул оксидов и их соединений. Например, из молекул оксидов (свободные оксиды): СаО, MgO, FeO, SiO2, P2O5 и их соединений: 2CaO·SiO2, 2FeO·SiO2, 2MnO·SiO2 и других. Соединения считаются полностью или частично диссоциированными на оксиды. Полагается, что в химических реакциях с металлом принимают участие только свободные оксиды, и активность любого оксида определяется концентрацией его молекул. Молекулярная теория относительно проста и (ранее имела широкое распространение) получила широкое применение в 11 металлургической практике. Главным ее недостатком (такого описания их поведения является несоответствие его физико-химической сущности ионного строения и механизма взаимодействия шлаков) отсутствие экспериментальных доказательств о наличии в шлаках молекул, т.е. группировок атомов с замкнутыми химическими связями. Доказано, что шлаки – ионные расплавы. Известны различные теории строения шлаков: теория совершенных ионных растворов, теория регулярных ионных растворов, полимерная теория шлаков и другие. Эти теории сложнее молекулярной и имеют свою теоретическую и экспериментальную базу. Они позволяют рассчитывать активности компонентов шлака, на основе методов математического моделирования. Имеются достаточно достоверные справочные данные об активности компонентов сталеплавильных шлаков [1,2]. Для поликомпонентных сталеплавильных шлаков активность FeO можно определить по диаграмме Чипмана [1]. На ней шестикомпонентный шлак, состоящий из оксидов кальция, магния, марганца, железа, кремния и фосфора, представлен как трехкомпонентный; CaO+MgO+MnO, FeO, SiO2+P2O5. Содержание компонентов выражено в мольных процентах. Диаграмма активности FeO в такой квазитройной системе приведена на рисунке 4. 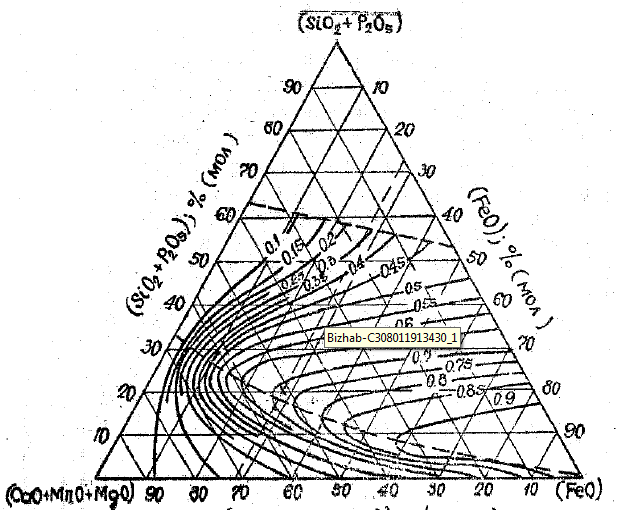 Рис. 4. Линии изоактивности для FeO (aFeO) в сталеплавильных шлаках (диаграмма Чипмана) Если концентрация компонента очень мала, то растворенное вещество ведет себя как идеальный газ. Реальные расплавы с малым содержанием примесей (чугуны, стали) не являются бесконечно-разбавленными и не подчиняются закону Генри. Поэтому в качестве стандартного состояния примеси удобнее принять, как отмечалось ранее, бесконечноразбавленный раствор c 1 % примеси. Известно, что активность компонента В в растворе А – В , где А является растворителем, обычно изменяется при добавлении в раствор других компонентов (С, D и т.д.). Для расплавов на основе железа (А) Вагнером был предложен метод, позволяющий определять активность любого компонента - примеси поликомпонентного сплава известного состава. Исходным положением является зависимость коэффициента активности компонента В fB от концентраций всех элементов-примесей: 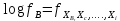 (15) (15)Уравнение концентрационной зависимости десятичного логарифма коэффициента активности записывается в виде ряда: 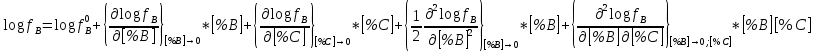 …. ….Производные 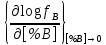 , ,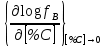 и т.д. называют параметрами взаимодействия первого порядка. Они показывают влияние добавляемых компонентов (С, D и т.д.) на коэффициент активности рассматриваемого компонента В при не больших концентрациях компонента В. В общем случае их обозначают: 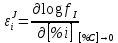 (17) (17)Производные 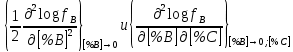 называют параметрами взаимодействия второго порядка и в общем случае обозначают как: 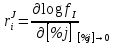 (18) (18)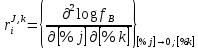 Параметры взаимодействия второго порядка показывают характер изменения параметров взаимодействия первого порядка 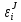 под влиянием увеличения концентрации компонентов в расплаве. При невысоких концентрациях растворенных компонентов (C, D, ..) слагаемыми, включающими параметры взаимодействия второго порядка под влиянием увеличения концентрации компонентов в расплаве. При невысоких концентрациях растворенных компонентов (C, D, ..) слагаемыми, включающими параметры взаимодействия второго порядка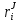 , ,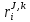 , можно пренебречь. , можно пренебречь. Тогда выражение (16), с учетом того, что 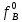 , запишется в виде: , запишется в виде: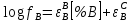 +[%C]+ +[%C]+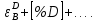 ФОРМУЛИРОВКА ЗАДАНИЯ 2.1. Определить активность оксида железа (FeO) в поликомпонентном шлаке (табл. 1); 2.2. Определить активность компонентов в сплавах на основе железа (табл. 2,3). Таблица 1 Состав шлакового расплава масс. %  Таблица 2 Химический состав железных сплавов (масс. %) 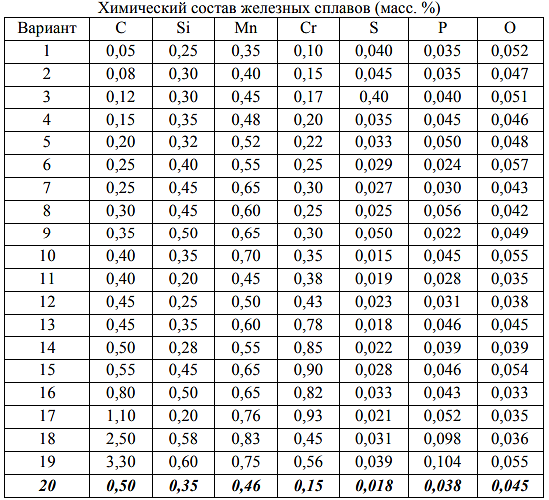 Таблица 3 Параметры взаимодействия εi j компонентов сплавов на основе железа при 1600 0С 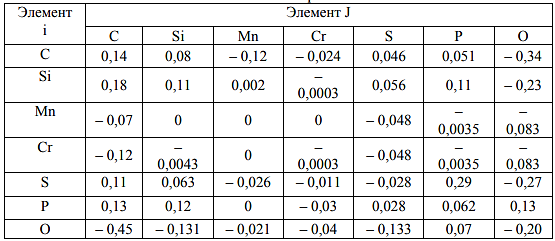 РЕШЕНИЕ ЗАДАНИЯ Задача №1 Определить активность FeO в шлаке, содержащем 35 % СаO; 5 % MgO; 5 % MnO;30 % FeO; 23 % SiO2; 2 % P2O5 по диаграмме Чипмана.  Рис 6. Линии изоактивности для FeO (aFeO) в сталеплавильных шлаках (диаграмма Чипмана) Следует пересчитать массовые проценты компонентов шлака ([%]) в мольные. Исходим из 100 г шлака. Он содержит 30 г. СаО, 5 г. MgO, 5 г.MnO, 30 г.FeO, 23 г. SiO2 и 2 г.P2O5. Определим количество молей каждого компонента ( ni ): 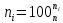 где i – относительная молярная масса оксида, а mi его масса. Если n – сумма молей оксидов шлака, то мольный процент Х (%) каждого компонента равен: Х (%) = 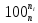 Результаты пересчета концентраций оксидов шлака приведены в таблице 4. Таблица 4 Пересчет состава шлака в мольные проценты
Таким образом, сумма основных оксидов СаО+MgO+MnO составит 50,158 мол. %. Сумма кислотных оксидов SiO2+P2O5: 24,267 мол. % и 25,573мол. % FeO. По диаграмме Чипмана такому составу шлака отвечает активность aFeO = 0,7 и коэффициент активности γFeO= aFeO/FeO = 2.73. Вывод: На основе таблицы 1 опытным путём было определено активность оксида железа (FeO) в поликомпонентном шлаке. Так же исходя из таблицы 2,3 было определено активность компонентов в сплавах на основе железа. Задача №2 Определить активности компонентов – примесей железного сплава, содержащего 0,25 %C, 0,45 % Si, 0,65 % Mn, 0,03 % Cr. 0,027 %S, 0,03%P, 0,043%O. Активности компонентов железного сплава определим по методу Вагнера, используя параметры взаимодействия первого порядка, приведенные в таблице 3. Уравнение (20) для углерода запишется так: lg fc =εc c [C] + εc Si[Si] + εc Mn[Mn] + εc Cr[Cr] + εc S [S] + εc P [P] + εc O[O] = 0,14 ·[C] + 0,08·[Si] – 0,12· [Mn] – 0,024·[Cr] + 0,046·[S] + 0,051·[P]-0,34·[O] =0,14·0,25+0,08·0,45–0,12·0,65– 0,024·0,3+0,046·0,027+0,051·0,03 –0,34·0,043 = -0,026. fc = - 1,584; ac = - 0,396. lg fSi =εSic [C] + εSiSi[Si] + εSiMn[Mn] + εSiCr[Cr] + εSiS [S] + εSiP [P] + εSiO[O] = 0,18·[C] + 0,11·[Si] +0,02·[Mn] – 0,0003·[Cr] + 0,056·[S] + 0,011·[P] – 0,23·[O] = 0,18·0,25+ 0,11·0,45 +0,02·0,65 – 0,0003·0,3 + 0,056·0,027 + 0,011·0,03 – 0,23·0,043 = 0,090. fSi =- 1,042; aSi =- 0,469. lg fMn =εMn c [C] + εMn Si[Si] + εMn Mn[Mn] + εMn Cr[Cr] + εMn S [S] + εMn P [P] + εMn O[O] = – 0,07· [C] + 0,0·[Si] – 0,0·[Mn] – 0,0·[Cr] – 0,048·[S] – 0,0035·[P] – 0,083·[O] = – 0,07 · 0,25–0,048·0,027 – 0,0035·0,03 – 0,083·0,043 = – 0,0258 fMn = -1,648; aMn =-1,071 lg fCr =εCr c [C] + εCr Si[Si] + εCr Mn[Mn] + εCr Cr[Cr] + εCr S [S] + εCr P [P] + εCr O[O] = – 0,12·[C] – 0,0043·[Si] – 0,0·[Mn] – 0,0003·[Cr] – 0,048·[S] – 0,0035·[P] – 0,083·[O] = – 0,12·0,25–0,0043·0,45 +0·0, 65 – 0,0003·0,3 – 0,048·0,027 – 0,0035·0,03 – 0,083·0,043= – 0,037. fCr = - 1,431; aCr =- 0,429. lg fS =εS c [C] + εS Si[Si] + εS Mn[Mn] + εS Cr[Cr] + εS S [S] + εS P [P] + εS O[O] = 0,11·[C] +0,063·[Si] – 0,026·[Mn] – 0,011·[Cr] – 0,028·[S] + 0,29·[P] – 0,27·[O] = 0,11 ·0,25+0,06343·0,45 – 0,026· 0, 65 – 0,011·0,3 – 0,028·0,027 + 0,29·0,03 – 0,27·0,043 = 0,0319 fS = - 1,495; aS =- 0,0332. lg fP =εP c [C] + εP Si[Si] + εP Mn[Mn] + εP Cr[Cr] + εP S [S] + εP P [P] + εP O[O] = 0,13·[C] +0,12·[Si] – 0,0· [Mn] – 0,03·[Cr] +0,028·[S] +0,062·[P] + 0,13·[O] = 0,13·0,25+0,12·0,45 +0·0, 65 – 0,03·0,3 + 0,028·0,027 + 0,062·0.03 + 0,013·0,043 = 0,0857 fP =- 1,0669; aP = -0,032. lg fO =εO c [C] + εO Si[Si] + εO Mn[Mn] + εO Cr[Cr] + εO S [S] + εO P [P] + εO O[O] = – 0,45·[C] – 0,131·[Si] – 0,021· [Mn] – 0,04·[Cr] – 0,133·[S] +0,07·[P] – 0,20·[O] = – 0,45·0,25– 0,131·0,45 – 0,021·0, 65 – 0,04·0,3 – 0,133·0,027 + 0,07·0,03 – 0,20·0,043 = – 0,207. fO = - 0,683; aO =- 0,0294 Таблица 2. Активности компонентов-примесей железного расплава при 1600 0С
Заключение Поскольку в очень разбавленных растворах концентрации компонентов, выраженные в различных единицах, пропорциональны друг другу, то это устраняет необходимость перевода процентов по массе, которыми обычно выражают состав растворов, в молярные доли. Если коэффициент активности 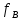 остается равным единице при увеличении концентрации до 1 %, то активность остается равным единице при увеличении концентрации до 1 %, то активность 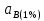 будет равна единице при концентрации компонента В, равной 1% по массе. Такой (реальный) 1% - ный раствор будет стандартным состоянием для рассматриваемого случая. Если же коэффициент активности будет равна единице при концентрации компонента В, равной 1% по массе. Такой (реальный) 1% - ный раствор будет стандартным состоянием для рассматриваемого случая. Если же коэффициент активности 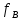 отклоняется от единицы уже при концентрациях ниже 1 % (рис. 2), то стандартным состоянием для такого случая будет гипотетический 1 % - ный раствор с таким же коэффициентом активности, как при бесконечном разбавлении. отклоняется от единицы уже при концентрациях ниже 1 % (рис. 2), то стандартным состоянием для такого случая будет гипотетический 1 % - ный раствор с таким же коэффициентом активности, как при бесконечном разбавлении. Метод Чипмана основан на молекулярной теории строения шлака. Она предполагает, что структурными компонентами шлака являются электронейтральные молекулы. Предполагается, что молекулы образующих шлак оксидов могут находиться в нем в свободном состоянии или вступать между собой в химические реакции с образованием разнообразных соединений. В соответствии со сделанными допущениями активность оксида в шлаке считают численно равной мольной доле свободного оксида. Модель «идеальный раствор» (раствор, в котором выполняется закон Рауля для любого компонента) предусматривает энергетическую неразличимость частиц Чипманом и Винклером предложен метод определения активности оксида железа и оксида кальция в основных сталеплавильных шлаках, которые не содержат Al2O3 и CaF2. Этот метод предполагает, что присутствующие в шлаке оксиды SiO2, P2O5 и Fe2O3 полностью связаны в соединения 4CaO*SiO2, 4CaO*P2O5 и CaO*Fe2O3. Тогда количество молей химических соединений в шлаке будет связано с числом молей отдельных оксидов соотношениями После образования химических соединений в шлаке остается некоторое количество свободного оксида кальция, при определении которого основные оксиды MgO и MnO считают эквивалентными оксиду кальция. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ Рыжонков Д.И., Арсентьев П.П., Яковлев В.В. и др. Теория металлургических процессов. М.: Металлургия, 1989. 392 с. 2. Казачков Е.А. Расчеты по теории металлургических процессов. М.: Металлургия, 1988. 288 с 3. Попель С.И., Сотников А.И., Бороненков В.Н. Теория металлургических процессов. М.: Металлургия, 1986. 463 с.. 4. Schlakenatlas. Dusseldorf: Stahleisen M.B.H., 1981. |
