Под взаимодействием излучений с веществом здесь понимаются лишь первичные элементарные акты взаимодействия частиц ионизирующего излучения с веществом, которые происходят под действием кулоновских, электромагнитных и ядерных сил. В данном разделе мы ограничимся рассмотрением взаимодействия с веществом заряженных частиц (в основном, электронов), фотонов и нейтронов.
4.1. Сечения взаимодействия
В силу статистической природы взаимодействия излучения с веществом для количественного описания этого процесса удобно пользоваться понятиями, имеющими вероятностный характер. Основополагающим при этом является понятие сечение взаимодействия (или поперечное сечение взаимодействия). Введем это понятие на примере взаимодействия γ-излучения.
Пусть в малой окрестности определенной точки пространства, где каким-либо источником фотонов создается поле γ-излучения с плотностью потока φ, помещается мишень, содержащая Δna атомов какого-нибудь элемента (рис. 1.9,а). Предположим, что ν падающих на мишень частиц испытывает в единицу времени взаимодействие с атомами мишени. Тогда сечением взаимодействия σ называется отношение
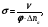 (1.37) (1.37)
имеющее размерность квадрата длины. Единицей измерения сечения в СИ является квадратный метр (допускается см2). В практике расчетов широкое распространение получила внесистемная единица барн (б) (1 б = 10-28 м2).
Для большей наглядности полезно также выразить смысл сечения взаимодействия через понятие вероятности. Поместим на пути мононаправленного пучка фотонов с плотностью потока φ образец вещества в виде тонкого цилиндра высотой dlи площадью основания S так, чтобы фотоны падали нормально к основанию (рис. 1.9,б). Если в единице объема данного вещества находится na атомов, то, исходя из формулы (1.9,6), полное число взаимодействий, которое будет иметь место в этом образце объемом dV= S·dl в единицу времени, равно
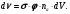 (1.38) (1.38)
Тогда вероятность для одного фотона испытать взаимодействие на пути в данном образце равна отношению числа фотонов, испытавших взаимодействие, к числу упавших на образец
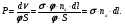 (1.39) (1.39)
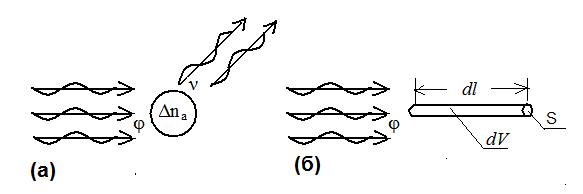
Рис. 1.9. К определению понятия поперечного сечения (а) и его вероятностной
интерпретации (б)
Теперь, если в формуле (1.39) положить na и dl равными единице, то вероятность P окажется численно равной сечению σ. Таким образом, сечение численно равно вероятности взаимодействия фотона (или другой элементарной частицы) на единичном пути в веществе, в единичном объема которого находится один атом (или электрон, или ядро, если сечение процесса определяется по отношению к взаимодействия с этими мишенями).
Сечения подразделяются на полные и парциальные. Полное сечение равняется сумме парциальных сечений, соответствующих различным видам взаимодействия (упругое и неупругое рассеяние, поглощение, различные ядерные реакции и т.д.). Эти виды для неделящихся ядер часто объединяют в две группы: сечение рассеяния и сечение поглощения. В соответствии с такой группировкой
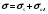 (1.40) (1.40)
где σs – сечение рассеяния; σa – сечение поглощения.
Все введенные выше сечения относились к процессам взаимодействия излучения с микрочастицами вещества (электроном, атомом, ядром), поэтому их часто называют микроскопическими интегральными сечениями. Их величина зависит от энергии налетающих частиц и от атомного номера атомов среды распространения (а для нейтронов и от массового номера атома).
Помимо интегральных сечений для описания вероятности изменения направления движения частицы с Ω на Ω' вводится понятие дифференциального сечения рассеяния 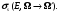
Микроскопическое дифференциальное сечение рассеяния численно равняется вероятности частицы ионизирующего излучения с энергией E при движении в гипотетическом веществе, имеющем в единице объема один атом, испытать на единице пути рассеяния, в ор1результате которого она изменит направление своего движения с Ω на Ω' в единице телесного угла вокруг Ω' (рис. 1.10). Размерность микроскопического дифференциального сечения рассеяния квадрат длины/стерадиан, обычно используется см2/стерад.
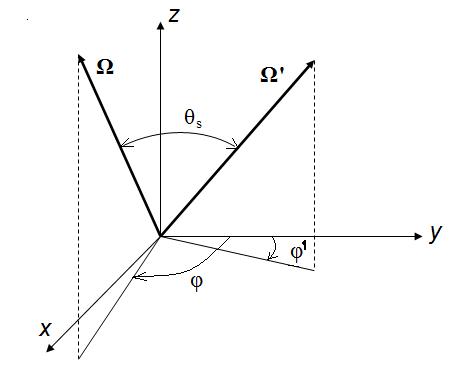
Рис. 1.10. К определению микроскопического дифференциального сечения
рассеяния
Как правило, дифференциальное сечение зависит не отдельно от направлений Ω и Ω', а от косинуса полярного угла между этими векторами и не зависит от азимутального угла, т.е.
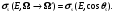 (1.41) (1.41)
При прохождении излучения через конкретное вещество вероятность взаимодействия падающей частице на единице пути в данном веществе в силу аддитивности процесса взаимодействия на отдельных атомах будет равна
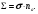 (1.41) (1.41)
Эту величину называют макроскопическим сечением взаимодействия и обозначают Σ. В случае γ-излучения макроскопическое сечение принято называть линейным коэффициентом ослабления фотонов и обозначать μ. Единицей измерения Σ и μ в СИ является м-1, но на практике допускается и чаще используется см-1.
Наряду с линейным коэффициентом ослабления широко используется также массовый коэффициент ослабления μm = μ/ρ, где ρ – плотность среды. Поэтому размерность μm [см2/г].
Взаимодействие заряженных частиц с веществом
Наибольший интерес для ЯМ из заряженных частиц представляют электроны и, частично, протоны и α-частицы. Поэтому, рассматривая их взаимодействие с веществом, основное внимание уделим электронам, хотя значительная часть материала с небольшими модификациями может быть применена к протонам и ионам.
При прохождении через вещество электрон испытывает кулоновское взаимодействие с орбитальными электронами и ядрами атомов. В результате взаимодействий электрон может терять свою кинетическую энергию (ионизационные и радиационные потери) или изменять направление своего движения, практически не теряя свою энергию (упругие столкновения). Количество взаимодействий у электронов с энергией 1 МэВ очень велико, так при замедлении от энергии 0,5 МэВ до 0,25 МэВ в алюминии электрон испытывает в среднем
3·104 взаимодействий. Поэтому в большинстве практических расчетов используются макроскопические понятия.
Столкновения между падающим электроном и орбитальными электронами или ядрами подразделяются на упругие и неупругие. При упругих столкновениях электрон отклоняется от направления своего первоначального движения, теряя при этом очень небольшую часть своей энергии. При неупругих взаимодействиях электрон изменяет направление движения и передает часть своей энергии орбитальному электрону или испускает ее в форме тормозного излучения.
Вид взаимодействия, который испытывает электрон с конкретным атомом зависит от так называемого прицельного параметра b, определяемого расстоянием между ядром атома и направлением движения электрона перед столкновением (рис. 1.11).
Для b >> a электрон испытывает дальнее (мягкое) столкновение с атомом в целом и передает орбитальным электронам небольшое количество энергии.
Для b ≈ a электрон испытывает близкое (жесткое) столкновение с орбитальными электронами и передает им значительную часть своей кинетической энергии, в результате чего образуются, так называемые δ-электроны.
Для b << a электрон испытывает радиационное взаимодействие с атомным ядром, испуская при этом тормозное излучение с непрерывным энергетическим спектром, простирающимся от нуля до начальной энергии электрона (рис. 1.12).
Количество мягких столкновений на порядки превышает количество жестких столкновений. Но интересно, что количество энергии, теряемой электроном в этих двух видах столкновений примерно одинаково.
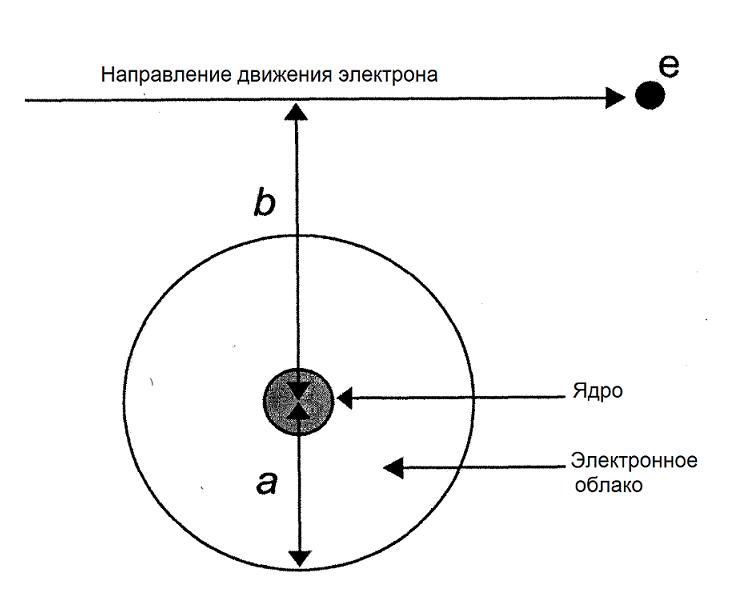
Рис. 1.11. Определение прицельного параметра
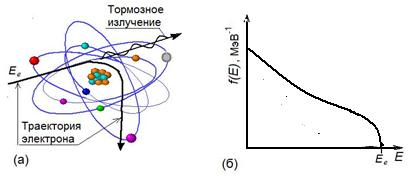
Рис.1.12. Образование (а) и примерный энергетический спектр тормозного
излучения, выходящего из тонкой мишени (б)
4.2.2. Взаимодействие с орбитальными электронами
При кулоновском взаимодействии между быстрыми заряженными частицами и орбитальными электронами последние можно считать свободными, если их энергия связи много меньше энергии, которую им передается в результате взаимодействия. Используя классическую нерелятивистскую теорию столкновений, Бор получил, что энергия Q, передаваемая в результате кулоновского взаимодействия заряженных частиц, равна
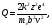 (1.42) (1.42)
где b– прицельный параметр; z – заряд первичной частицы (в единицах заряда электрона); v – скорость первичной частицы; k – константа, равная 8,9875·109 Н·м2·Кл-2.
Отметим, что масса первичной частицы не входит в формулу (1.42), т.е. она применима и для протонов и других заряженных частиц. Уравнение (1.42) приводит к следующему классическому выражению для поперечного сечения, дифференциального по передаваемой энергии и отнесенного к одному электрону:
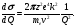 (1.43) (1.43)
Релятивисткий квантово-механический вариант поперечного сечения кулоновского взаимодействия между свободными электронами был получен Меллером
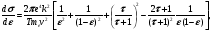 (1.44) (1.44)
где T – кинетическая энергия электрона; ε = Q/T – передаваемая энергия в единицах кинетической энергии электрона; τ = T/mec2; v – скорость электрона.
Основной вклад в сечение (1.44) вносит первый член. Если пренебречь остальными членами, то выражение (1.44) переходит в классическое (1.43). Имеющаяся в обеих формулах зависимость 1/Q2 показывает, что доминирующими являются малые потери энергии. Средняя величина потери энергии электроном в средах с низкими атомными номерами составляет
60 эВ.
Кулоновское взаимодействия между электроном и орбитальными электронами атомов среды приводит в результате к ионизации и возбуждению атомов. Ионизация заключается в вырывании электронов из атомов. Возбуждение переводит орбитальные электроны на более высокие орбиты. В результате обоих процессов электрон теряет часть своей кинетической энергии, что количественно описывается через понятие ионизационная тормозная способность.
4.2.3. Взаимодействие с ядрами атомов
Когда заряженная частица пролетает близко к атомному ядру, то кулоновское взаимодействие происходит скорее не с орбитальными электронами, а непосредственно с ядром. Если заряженной частицей является электрон, то это взаимодействие приводит к отклонению его от первоначального направления движения (упругому рассеянию), при котором энергия электрона практически совсем не изменяется. Другим результатом взаимодействия с ядром может явиться испускание тормозного излучения, при котором происходит уже значительная потеря энергии.
Дифференциальное сечение упругого рассеяния было получено Резерфордом и впоследствии уточнялось несколькими авторами, в том числе Моттом и Мольером, которые предложили метод учета эффект экранирования поля ядра орбитальными электронами. В этом варианте дифференциальное сечение имеет следующий вид:
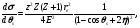 (1.45) (1.45)
где z, Е – заряд и энергия налетающей частицы; θs – угол рассеяния; η – параметр экранирования.
Угловое распределение частиц после упругого рассеяния имеет очень большую вытянутость вперед (максимум сечения при θs
0), но так как общее количество упругих столкновений очень велико, то в результате в сумме они приводят к существенному изменению траектории первичной частицы. В качестве примера на рис. 1.13 приводится снимок траекторий электронов в пузырьковой камере, наполненной пропаном

Рис. 1.13. Снимок узкого пучка электронов с энергией 9,3 МэВ в пузырьковой камере, наполненной пропаном [3]
Потери энергии заряженными частицами на тормозное излучение пропорциональны
(Z/m), где Z – заряд ядра и m – масса первичной частицы. Отсюда следует малая вероятность рождения тормозного излучения при прохождении через вещество тжелых заряженных частиц. Поперечное сечение образования тормозного излучения имеет очень сложный вид. Его особенностью является то, что
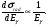 (1.46) (1.46)
Поэтому средние потери энергии при испускании тормозного излучения заметно выше, чем при столкновениях. Количественно эти потери обычно характеризуется радиационной тормозной способностью. Для оценки мощности тормозного излучения P можно применить ларморовского соотношение, устанавливающее, что мощность эмиссии фотонов, создаваемых ускоряемой частицей с зарядом z, пропорциональна квадрату ускорения a и квадрату заряда:
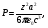 (1.47) (1.47)
где ε0 – тттттттт
Угловое распределение испускаемого тормозного излучения\ пропорционально 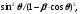 где θ – угол между ускорением заряженной частицы и единичным вектором, связывающим заряд и точку наблюдения; β – стандартное релятивистское отношение v/c. При небольших скоростях v заряженной частицы угловое распределение пропорционально sin2θ, т.е. имеет максимум при θ = 90о. Однако при увеличении скорости до где θ – угол между ускорением заряженной частицы и единичным вектором, связывающим заряд и точку наблюдения; β – стандартное релятивистское отношение v/c. При небольших скоростях v заряженной частицы угловое распределение пропорционально sin2θ, т.е. имеет максимум при θ = 90о. Однако при увеличении скорости до
с, угловое распределение приобретает большую вытянутость вперед. Направление максимальной эмиссии тормозных фотонов можно рассчитать из следующего выражения:
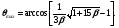 (1.48) (1.48)
Из формулы (1.48) следует, что при 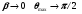 и при и при 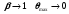 . Это указывает, что в диагностической радиологии (ортовольтовые пучки) большая часть рентгеновского излучения испускается под углом 90о по отношению к направлению падения пучка электронов на мишень, в то время как в мегавольтном диапазоне (линейные медицинские ускорители электронов (ЛУЭ)) угол максимальной интенсивности близок 0о. . Это указывает, что в диагностической радиологии (ортовольтовые пучки) большая часть рентгеновского излучения испускается под углом 90о по отношению к направлению падения пучка электронов на мишень, в то время как в мегавольтном диапазоне (линейные медицинские ускорители электронов (ЛУЭ)) угол максимальной интенсивности близок 0о.
Потери энергии на тормозное излучение прямо пропорциональны атомному номеру среды и кинетической энергии электронов. Выход х-лучей из мишеней в энергетическом диапазоне диагностической радиологии (
100 кэВ) составляет
1%, а в мегавольтном диапазоне энергий выход
10 – 20 %.
4.2.4. Тормозная способность
Число взаимодействий электронов с атомами среды, как отмечалось выше, на много порядков превышает число взаимодействий, которое испытывают фотоны до своего поглощения в веществе. Поэтому для количественного описания взаимодействия электронов с веществом в дозиметрии используются, в основном, не микроскопические сечения отдельных процессов, а макроскопические характеристики, связанные со скоростью потери электроном своей энергии на единице пути в конкретном веществе.
Наиболее употребительной величиной, характеризующей свойства вещества по отношению к поглощению энергии электронов, является понятие полной массовой тормозной способности – (S/ρ)tot. Под этой величиной в соответствии с рекомендациями Международной комиссии по радиационным единицам (МКРЕ) понимается отношение dEк произведению ρ∙dl, где dE – полные потери кинетической энергии электрона при прохождении им пути dlв материалес плотностью ρ. Кроме плотности эта величина зависит также от атомного номера материала Zи энергии электрона E. Принято представлять (S/ρ)totв соответствии с разными видами потерь энергии в виде суммы:
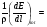 (S/ρ)tot= (S/ρ)col + (S/ρ)rad, (1.49) (S/ρ)tot= (S/ρ)col + (S/ρ)rad, (1.49)
где (S/ρ)col – связана с потерями электроном энергии на ионизацию и возбуждение атомов среды и называется массовой тормозной способностью столкновений; (S/ρ)rad – связана с потерями электроном энергии на испускание тормозного излучения и называется радиационной массовой тормозной способностью. Обычно используемая размерность массовой тормозной способности Мэв/(см2·г).
Массовая тормозная способность столкновений может быть рассчитана из выражения, приводимого, например, в работе [3]:
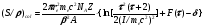 , (1.50) , (1.50)
где δ – поправка на эффект плотности вещества; τ = E/mec2– отношение кинетической энергии Tчастицык энергии массы покоя электрона; re– классический радиус электрона; Z– атомный номер среды; A– атомный вес вещества; I– средний ионизационный потенциал вещества;
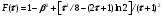 . (1.51) . (1.51)
Интересно отметить, что величина (S/ρ)col выше для материалов с низким атомным номером. Это является следствием того, что материалы с высоким атомным номером имеют меньше электронов на грамм вещества, чем материалы с низким атомным номером.
Для расчета массовой тормозной способности частиц более тяжелых , чем электроны в работе [3] рекомендуется формула, полученная Аттиксом:  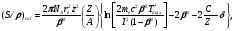
(1.52)
где T'max – максимальная энергия, которая в одном столкновении может передаваться электронам (например, для 10 МэВ протонов T'max=20 кэВ, в то время как для электронов той же начальной энергии T'max= 5 МэВ).
Если кинетическая энергия первичной заряженной частицы T< M0c2, то 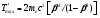 . Уравнение (1.52), следуя Аттиксу, можно упростить до следующего выражения: . Уравнение (1.52), следуя Аттиксу, можно упростить до следующего выражения:
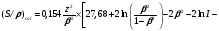
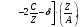 (1.53) (1.53)
где C/Z – так называемая оболочечная поправка. Она необходима, потому что приближение Борна (2Zz/137 << β) не действует при приближении скорости частицы к скорости орбитальных электронов.
Радиационная массовая тормозная способность не может быть выражена в простой общей форме для всех энергий и веществ. Приведем здесь формулу [4] для электронов высоких энергий (случай полного экранирования: τ >> 1/αZ1/3 ):
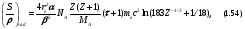 где α – постоянная тонкой структуры. где α – постоянная тонкой структуры.
Как видно из формулы (1.54), (S/ρ)rad растет почти линейно с увеличением кинетической энергии электрона в мегавольтной области, в то время как (S/ρ)col имеет в этом районе слабую логарифмическую зависимость (1.54). В более широком энергетическом диапазоне зависимость этих величин от энергии электрона демонстрируется для воды и свинца на рис. 1.14. Отметим также существенно более сильную зависимость (S/ρ)rad от атомного номера среды, чем имеет место для (S/ρ)rad.
Используя массовую тормозную способность, можно определить пробег электрона, R, с энергией Ee
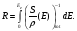 (1.55) (1.55)
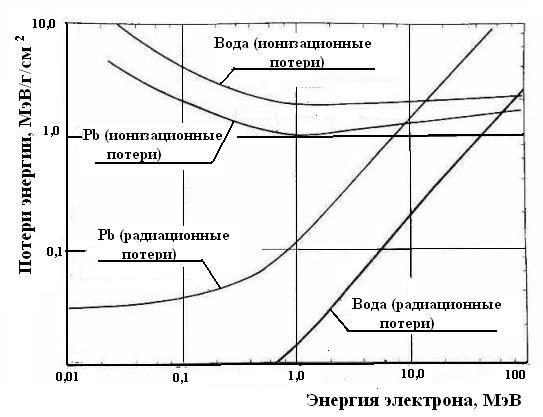
Рис. 1.14. Зависимость массовых тормозных способностей электронов от энергии для воды и свинца: 1 – (S/ρ)col; 2 – (S/ρ)rad; —— – данные для воды; – – – данные для свинца (адаптировано из [4])
4.2.5. Ограниченная массовая тормозная способность и поглощенная доза
При неупругом взаимодействии с веществом электрон, как отмечалось выше, может передать часть своей энергии электронам среды (вторичным электронам) или испустить тормозное излучение. В большинстве случаев вторичные электроны получают относительно небольшую долю энергии первичных электронов, но имеют место и случаи большой передачи энергии (до половины от энергии первичного электрона, а если передается больше половины, тогда вторичный электрон называют первичным, а вторичный – первичным). Такие высокоэнергетические вторичные электроны имеют уже достаточно большие пробеги в веществе и, следовательно, потеряют свою энергию на некотором удалении от точки образования. Аналогичная ситуация имеет место и для тормозных фотонов. Так как понятие поглощенной дозы D связывается с локальным поглощением энергии, то для расчета величины D(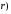 , исходя из знания пространственно-энергетического распределения флюенса электронов , исходя из знания пространственно-энергетического распределения флюенса электронов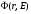 , использование понятия массовой тормозной способности будет некорректным. Для определения связи между этими двумя величинами вводится понятие ограниченной тормозной способности столкновений. , использование понятия массовой тормозной способности будет некорректным. Для определения связи между этими двумя величинами вводится понятие ограниченной тормозной способности столкновений.
Ограниченная тормозная способность столкновений относится к концепции линейной потери энергии. Под понятием линейной передачи энергии L понимается отношение энергии dE, теряемой заряженной частицей на ионизацию и возбуждение атомов среды, к величине пути dl, т.е.L=(dE/dl). Таким образом, в величину Lне входят потери энергии на испускание тормозного излучения. Чтобы отделить локальное поглощение энергии, имеющее место вблизи точки взаимодействия, от энергии, которая будет потеряна электроном на определенном расстоянии от точки взаимодействия, вводится понятие ограниченной тормозной способности столкновений, (L/ρ)col,Δ. Другими словами, величина (L/ρ)col,Δ представляет собой частное от деления dEнаρ∙dl, при условии, что в dE включаются все потери энергии, величина которых меньше Δ:
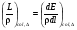 (1.56) (1.56)
Выбор значения Δ зависит от специфики рассматриваемой проблемы. Для задач, связанных с расчетом ионизационных камер значение Δ берется равным 10 кэВ, что соответствует пробегу электрона в воздухе порядка 2 мм. Для микродозиметрических расчетов обычно берут Δ = 100 эВ. На рис. 1.15 приводятся для сравнения массовые тормозные способности с разными значениями Δ.
Количественные значения ограниченной тормозной способности для различных значений Δ и веществ были рассчитаны в работе [6]. Используя это понятие, значение поглощенной дозы, создаваемой электронами, можно определить из следующего выражения:
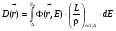 . (1.57) . (1.57)
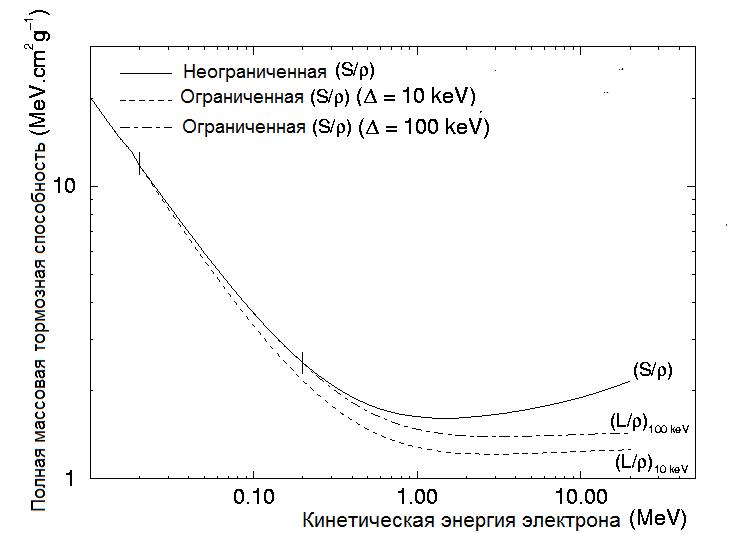
Рис.1.15. Зависимости массовой тормозной способности от значения Δ
(адаптировано из [1])
4.2.6. Угловое распределение рассеянных электронов и массовая рассеивающая способность
При прохождении пучка электронов через вещество последние, как отмечалось выше, под действием кулоновских сил испытывают очень большое количество взаимодействий. В результате электроны приобретают составляющие скорости и смещения перпендикулярные к направлению их первоначального движения (см. рис. 1.13). Для большинства практических задач угловое и пространственное расширение узкого коллимированного пучка (тонкого луча) электронов в малоугловом приближении может быть аппроксимировано гауссовским распределением [7].
Пусть такой узкий пучок падает на плоскую поверхность рассеивателя вдоль оси z(геометрическая ось пучка параллельна оси z), которая, в свою очередь, нормальна к этой поверхности. Тогда угловое распределение флюенса электронов после прохождения ими слоя рассеивателя толщиной z , будет описываться выражением, предложенным в работах [7,8]:
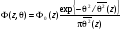 , (1.58) , (1.58)
где θ – угол по отношению к оси z; 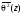 – средний квадрат углового расширения пучка; – средний квадрат углового расширения пучка; 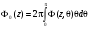 . .
Значение 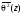 определяется из выражения: определяется из выражения:
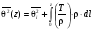 , (1.59) , (1.59)
где (T/ρ) – массовая угловая рассеивающая способность, значения которой для некоторых веществ приводятся в работах [5, 9]; 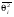 – начальное значение среднего квадрата углового расширения пучка. – начальное значение среднего квадрата углового расширения пучка.
По аналогии с массовой тормозной способностью МКРЕ [9] определяет массовую угловую рассеивающую способность как отношение приращения среднего квадрата угла рассеяния к 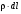 : :
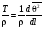 . (1.60) . (1.60)
Эксперименты показывают, что для материалов с низким атомным номером наблюдается линейная зависимость между 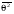 и глубиной проникновения пучка в достаточно широком интервале глубин [6,10]. С дальнейшим с увеличением глубины формируется равновесное угловое распределение, так как электроны, рассеянные на большие углы, быстро выбывают из пучка. Массовая угловая рассеивающая способность пропорциональна примерно квадрату атомного номера вещества и обратно пропорциональна кинетической энергии электрона. и глубиной проникновения пучка в достаточно широком интервале глубин [6,10]. С дальнейшим с увеличением глубины формируется равновесное угловое распределение, так как электроны, рассеянные на большие углы, быстро выбывают из пучка. Массовая угловая рассеивающая способность пропорциональна примерно квадрату атомного номера вещества и обратно пропорциональна кинетической энергии электрона.
Взаимодействие фотонов с веществом Общее рассмотрение
При прохождении через вещество фотоны испытывают взаимодействие с сильно связанными электронами, т.е. с атомом как с целым (фотоэлектрический эффект, когерентное рассеяние) с полем ядер (образование электроно-позитронных пар) или со свободными электронами (эффект Комптона, образование триплетов).
В контексте фотонных взаимодействий связанный электрон – это орбитальный электрон с энергией связи на оболочке порядка или немного выше, чем энергия фотонов, в то время как свободный электрон – это электрон с энергией связи много меньшей, чем энергия фотона.
В области энергий фотонов от нескольких кэВ до нескольких МэВ, представляющих наибольший интерес для ЯМ основными процессами взаимодействия фотонов с веществом являются фотоэлектрический эффект, комптоновское рассеяние и образование электронно-позитронных пар. Значительно меньшую роль играют когерентное (или томсон-релеевское рассеяние) на связанных электронах и фото-ядерные реакции. Во время взаимодействия фотоны могут полностью исчезнуть (фотоэффект, образование пар и триплетов) или рассеяться когерентно(когерентное рассеяние) или некогерентно (эффект Комптона). Поперечные сечения взаимодействия фотонов зависят от их энергии Eγ и от атомного номера среды Z.
Фотоэлектрический эффект
При фотоэлектрическом эффекте фотон взаимодействует с орбитальным электроном, находящимся на i-оболочке, и поглощается, передавая всю свою энергию этому электрону, который в результате выбивается из атома с кинетической энергией
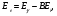 (1.61) (1.61)
где BEi– энергия связи на i-оболочке.
После выбивания связанного электрона появившаяся на оболочке свободная вакансия заполняется электроном с вышерасположенной оболочки и событие фотопоглощения заканчивается испусканием характеристического фотона или электрона Оже (рис. 1.16).
При Eγ > BEK основную роль в фотоэффекте играют электроны на К-оболочке, и сечение фотоэффекта σф на К-оболочке составляет 80 % от полного сечения фотоэффекта. При Eγ < BEK процесс будет идти на других оболочках. Поэтому в зависимости σф от энергии фотонов наблюдаются скачки при энергиях фотонов, равных энергии связи на K, L, M- и других оболочках.
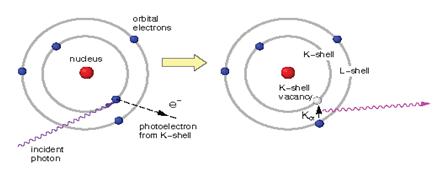
Рис. 1.16. Схематическое изображение фотоэлектрического поглощения фотона и последующего испускания характеристического фотона
Существует немало формул, в том числе и теоретических, выражающих зависимость σф от Eγ и от Z. Однако все они имеют приближенный характер, поэтому на практике лучше пользоваться справочными данными. Качественная зависимость σф на К-оболочке от этих переменных для фотонов больших энергий (Eγ >> mec2) описывается формулой Заутера:
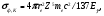 (1.62) (1.62)
где re= e2/(mec2) =2,82·10-15 м – классический радиус электрона.
Для нерелятивистской области (BEK < Eγ << mec2) справедлива приближенная формула Гайтлера
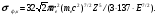 (1.63) (1.63)
Как видно из (1.62) и (1.63) σф,к убывает в релятивистской области значительно медленнее (1/E), чем в нерелятивистской области (E-7/2). Полное сечение фотоэффекта при Eγ > BEK связано с σф,к следующей формулой (погрешность 2 – 3 %):
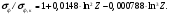 (1.64) (1.64)
Таким образом, сечение фотоэффекта сильно зависит от атомного номера среды (
Z5) и быстро убывает с ростом энергии фотона (рис. 1.17). Поэтому этот эффект играет особо существенную роль в области малых энергий фотонов и для веществ с большим Z.
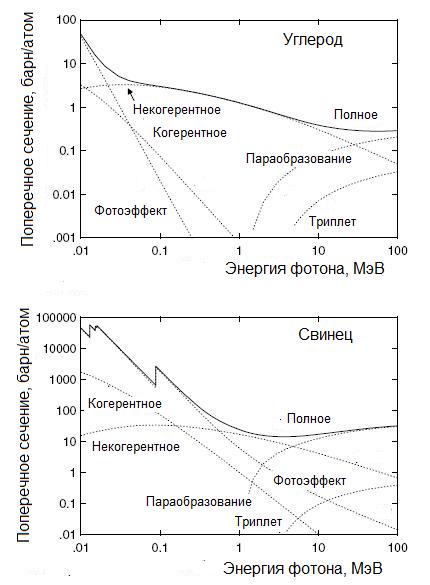
Рис.1.17. Зависимость микроскопических сечений взаимодействия фотонов, отнесенная к одному атому, от энергии фотонов углерода и свинца
Средняя энергия, передаваемая в среде электронам при фотоэффекте фотонов с энергией Eγ > BEK , равна
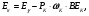 (1.65) (1.65)
где PK – доля событий фотоэффекта, происходящих на K-оболочке;
ωК – выход характеристического излучения с К-оболочки. Величина PK изменяется от 1.0 для элементов с малым Z до 0,8 для элементов с большим Z.
Комптоновское (некогерентное) рассеяние
При комптоновском рассеянии фотоны, как следует из названия эффекта не поглощаются, а в результате взаимодействия со "свободным" электроном передают ему часть своей энергии и сами отклоняются от направления своего первоначального движения на угол θs (рис. 1.18).
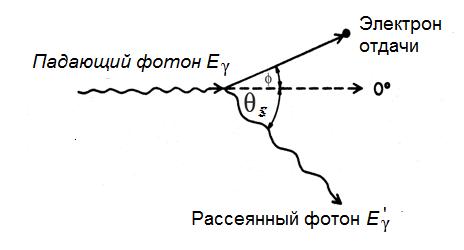
Рис. 1.18. Диаграмма комптоновского рассеяния фотонов
Так как скорость орбитальных электронов мала по сравнению со скоростью света, при Eγ ≥ EKэлектрон до взаимодействия с фотоном можно считать свободным и покоящимся. Отсюда потерю энергии и угол рассеяния фотона возможно связать с помощью уравнений закона сохранения и импульса, как при упругом рассеянии:
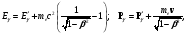 (1.66) (1.66)
где Eγ и E' – энергия фотона до и после рассеяния; Pγ и Pγ' – импульсы фотона до и после рассеяния (|P| = E/c); v – скорость электрона отдачи.
В результате преобразования уравнений (1.66) получаем следующие соотношения:
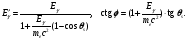 (1.67) (1.67)
Из уравнения (1.67) следует, что с увеличением угла рассеяния θs энергия, уносимая рассеянным фотоном уменьшается, а энергия, передаваемая электрону отдачи, возрастает. Минимальная значение E'γ, соответствующей рассеянию на угол θs = 180о, равно
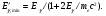 (1.68) (1.68)
Как видно из выражения (1.68), для фотонов с высокой энергией (Eγ/mec2 >> 1) минимальная энергия рассеянных фотонов стремится к mec2/2 = 0,255 МэВ, т.е. потеря энергии очень значительна. В области же низких начальных энергий (Eγ/mec2 << 1) наоборот, минимальное энергия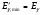 , т.е. потери энергии в результате комптоновского рассеяния незначительны. , т.е. потери энергии в результате комптоновского рассеяния незначительны.
Так как комптоновское рассеяние имеет место на свободных электронах, то микроскопическое сечение, отнесенное к одному электрону σк,e, не зависит от атомного номера среды Z, а отнесенное к одному атому линейно зависит от Z(для элементов с малым и средним Z). Для веществ с большим Z зависимость σк,e появляется (не очень сильная) из-за эффекта экранирования полей электронных оболочек.
С увеличением начальной энергии фотонов σк,eпостепенно уменьшается от значения 0.665 10-24 см2/электрон при очень низких энергиях до 0,051 10-24 см2/электрон при очень низких энергиях до 0,051 10-24 см2/электрон при Eγ = 10 МэВ (рис. 1.16). 10-24 см2/электрон при Eγ = 10 МэВ (рис. 1.16).
Угловое распределение рассеянных фотонов определяется дифференциальным сечением рассеяния. Согласно теории Клейна-Нишины-Тамма это сечение, отнесенное к одному атому равно
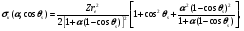
(1.69)
где α = Eγ/mec2 – безразмерная начальная энергия фотона.
Зависимость микроскопического дифференциального сечения комптоновского рассеяния от угла рассеяния для разных начальных энергий фотонов показана на рис. 1.19,a. Из приводимых графиков наглядно видно, что с увеличением энергии фотонов возрастает анизотропия рассеяния, проявляющаяся во все большей вытянутости вперед рассеянных фотонов.
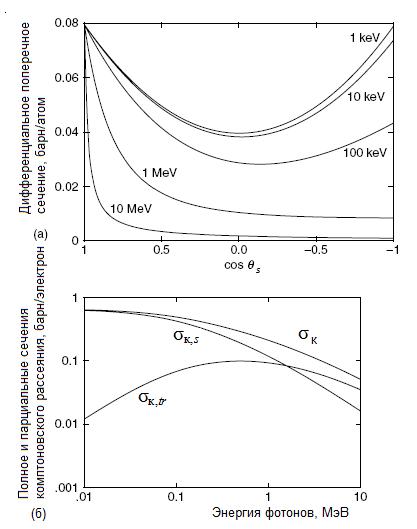
Рис. 1.19. Зависимость микроскопического дифференциального сечения комптоновского рассеяния от косинуса угла рассеяния для разных начальных энергий фотонов (а), и зависимость полного и парциальных сечений комптоновского рассеяния от энергии фотонов (б)
Важной характеристикой комптоновского рассеяния является средняя относительная потеря фотоном энергии в этом процессе
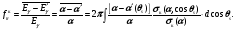 (1.70) (1.70)
Данная величина пропорциональна энергии, передаваемой комптоновским электронам отдачи. На рис. 1.20 показана зависимость этой величины от начальной энергии фотонов. Из рис. 1.20 видно, что доля энергии, передаваемая комптоновским электронам с ростом энергии фотонов возрастает. Так 1 МэВ фотоны при комптоновском рассеянии в среднем передают электронам отдачи 440 кэВ и 560 кэВ рассеянным фотонам, 100 кэВ фотоны 15 кэВ и 85 кэВ и 10 МэВ фотоны 6,9 МэВ и 3,1 МэВ соответственно.
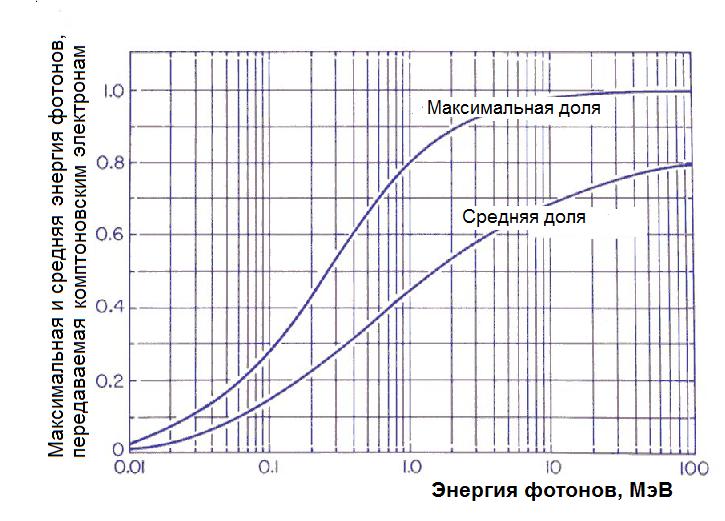
Рис. 1.20. Зависимость максимальная и средняя доля энергии фотонов, передаваемая в среду комптоновским электронам в зависимости от начальной энергии фотонов [1]
При расчете кермы и поглощенной дозы необходимо учитывать, что комптоновское рассеяние сопровождается передачей комптоновским электронам только части энергии фотона. Поэтому для выполнения таких расчетов целесообразно разделить сечение комптоновского рассеяния на две составляющие:
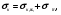 (1.71) (1.71)
где 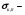 принято называть сечением передачи энергии при комптоновском взаимодействии; принято называть сечением передачи энергии при комптоновском взаимодействии; 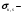 сечением рассеяния энергии при комптоновском взаимодействии. Эти величины определяются из следующих уравнений. сечением рассеяния энергии при комптоновском взаимодействии. Эти величины определяются из следующих уравнений.
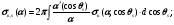 (1.72) (1.72)
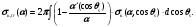 (1.73) (1.73)
Зависимость парциальных составляющих сечения комптоновского взаимодействия от начальной энергии фотонов показано на рис. 1.19,б. В зависимости 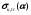 наблюдается пик, что связано с небольшими потерями энергии фотонами при их комптоновском взаимодействии в области малых энергий. наблюдается пик, что связано с небольшими потерями энергии фотонами при их комптоновском взаимодействии в области малых энергий.
Когерентное (релеевское) рассеяние
При когерентном рассеянии фотон взаимодействует со связанным орбитальном электроном, т.е. с атомом как целом. В результате когерентного рассеяния фотон только отклоняется на небольшой угол относительно направления первоначального движения, практически не изменяя свою энергию. Дифференциальное микроскопическое сечение когерентного рассеяния имеет следующий вид:
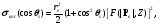 (1.74) (1.74)
где F(|Pe|,Z) – формфактор представляет вероятность передачи импулься |Pe| совокупности Z электронов атома. В первом приближении F
Z2, что указывает на возрастании роли когерентного рассеяния для материалов с высоким Z. Интегральное микроскопическое сечение когерентного рассеяния, отнесенное к одному атому, пропорционально
(Z/Eγ)2. Так, например, для 1 МэВ фотонов отношение сечений когерентного и комптоновского рассеяния возрастает от 10-3 для легких до 0,05 для тяжелых элементов.
Образование электронно-позитронных пар
Эффект образования электронно-позитронной пары состоит в образовании фотоном в поле ядра пары заряженных частиц: электрон и позитрон. Сам фотон при этом исчезает, а его энергия идет на создание двух масс покоя (2mec2 = 1,022 МэВ) и кинетической энергии заряженным частицам и энергию отдачи ядра (
5 кэВ), которая делится между частицами поровну. Таким образом, энергетическая зависимость сечения этого процесса σп имеет пороговый характер (см. рис. 1.17) с порогом Eпор
1,02 МэВ и монотонно возрастает с увеличением энергии фотонов до примерно постоянного значения в области энергий
50 МэВ.
Когда образование пары происходит в поле орбитального электрона, то этот процесс называется образование триплета (электрон, позитрон и орбитальный электрон) и кинетическая энергия распределяется уже между тремя частицами. Порог данного эффекта равен 4mec2. Сечение образования пар в поле орбитального электрона пропорционально Z, а в поле ядра пропорционально Z2. Абсолютная величина сечения σп в поле орбитального электрона много меньше (примерно в 50 раз) сечения образования пар в поле ядра.
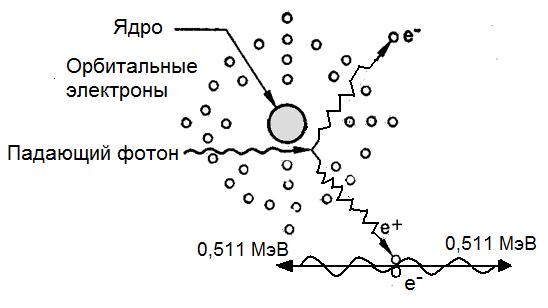
Рис. 1.21. Схематическое изображение эффекта образования пары: электрон
и позитрон
Электрон и позитрон испускаются главным образом в том же направлении, в каком двигался родительский фотон, точнее в пределах телесного угла 0,511/Eγ радиан. Свободный позитрон нестабилен и преимущественно в конце пробега аннигилирует с одним из электронов среды. В результате аннигиляции образуются два фотона с энергией по 0,511 МэВ (рис. 1.21). Поскольку аннигиляция имеет наибольшую вероятность при малых энергиях позитрона, угол между направлениями разлета аннигиляционных фотонов составляет
180о.
Фотоядерные реакции
При фотоядерной реакции высокоэнергетичный фотон поглощается ядром атома. В результате происходит эмиссия нейтрона ((γ,n)-реакция) или протона ((γ,р)-реакция) и ядро трансформируется в радиоактивный продукт. Данная реакция имеет пороговый характер и происходит при превышении энергии фотона над энергией связи нуклонов в ядре. В большинстве случаев эта энергия равна 6 – 8 МэВ. Исключение составляют дейтерий и бериллий, для которых пороговая энергия реакции ((γ,n) довольно мала (2,23 и 1,665 МэВ).
Данная реакция слабо влияет на распространение фотонов в среде из-за ее малой вероятности. Даже для тяжелых ядер сечение процесса не превышает 1 б. Однако ее следует учитывать при работе медицинских ускорителей, так как возникающие потоки нейтронов могут приводить к заметной активации оборудования.
Полные микроскопические и макроскопические сечения взаимодействия фотонов
Полное микроскопическое сечение взаимодействия фотонов представляет сумму всех парциальных сечений:
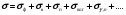 (1.75) (1.75)
Однако в практических расчетах прохождения фотонов через среды обычно не учитываются процессы, слабо влияющие на перенос излучения. К таким процессам относится когерентное рассеяние, не изменяющее энергию фотонов, образование триплетов, (γ,n)-реакция и др. Таким образом, учитываются только три основных вида взаимодействия, поэтому полное сечение равно
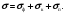 (1.76) (1.76)
Характерной особенностью зависимости σ(E) является наличие минимума. Он объясняется убыванием сечений фотоэффекта и комптоновского рассеяния с ростом энергии фотонов и возрастанием сечения образования пар. Положение минимума зависит от атомного номера вещества. Так для азота энергия минимума соответствует 45 МэВ, а для свинца 3,4 МэВ. Полезно выделить для разных материалов области энергии, где тот или иной эффект играют наиболее важную роль. Подобное выделение таких областей проводится на рис. 1.22.
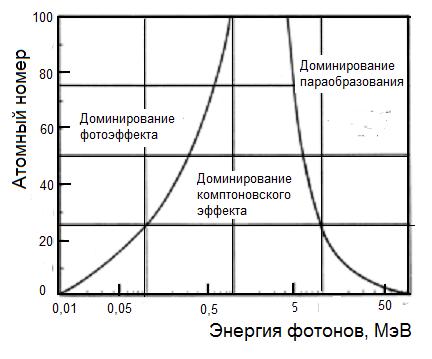
Рис.1.22. Области относительного доминирования одного из трех основных видов взаимодействия фотонов с веществом (адаптировано из [1])
Макроскопические сечения взаимодействия фотонов с веществом, как отмечалось в разделе 4.1, принято называть линейными μ и массовыми μm коэффициентами ослабления γ-излучения. Они определяются из следующих очевидных формул:
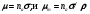 (1.77) (1.77)
Физический смысл этих величин был определен в разделе 4.1. Интересно сравнить зависимости массовых коэффициентов ослабления фотонов от энергии для разных материалов (рис. 1.23). Отметим такой непривычный факт, что в области энергий от 1 до 4 МэВ значение μm для воды больше, чем для свинца.
Линейные и массовые коэффициенты ослабления фотонов используются для расчета прохождения γ-излучения через материалы в условиях "хорошей" геометрии или геометрии узкого пучка. Особенностью такой геометрии является то, что в детектор попадает (или детектор регистрирует) только первичное (нерассеянное) излучение источника фотонов. В этих условиях плотность потока (или флюенс) излучения за слоем материала толщиной t для мононаправленного моноэнергетического источника равна
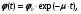 (1.78) (1.78)
где φ0 – плотность потока γ-излучения, падающего на слой материала, т.е. при t = 0.
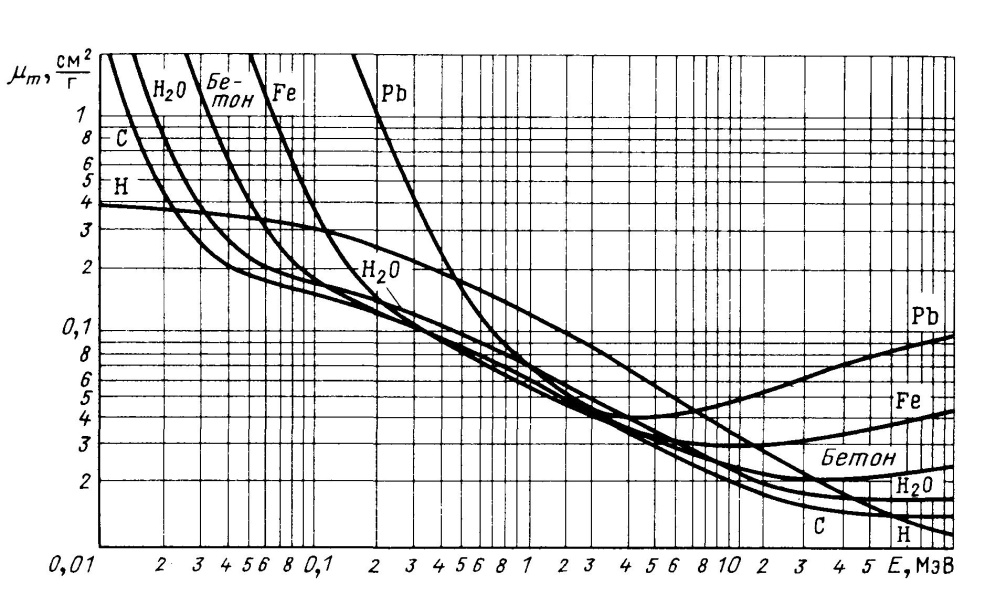
Рис. 1.23. Зависимость массового коэффициента ослабления фотонов для разных материалов от начальной энергии фотонов [11]
Однако на практике часто требуется знать не потоковые, а дозовые характеристики поля (мощность кермы и мощность поглощенной дозы или керму и поглощенную дозу). Данные характеристики связаны с плотностью потока энергии или флюенсом энергии (см. формулы (1.29 – 1.32) и (1.34)) через массовые коэффициенты передачи энергии (μ/ρ)tr и поглощения энергии (μ/ρ)en. Расчет этих коэффициентов выполняется с учетом той доли энергии фотона, которая при конкретном виде взаимодействия передается электронам среды. Соответствующая формула для (μ/ρ)tr имеет следующий вид:
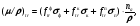 (1.79) (1.79)
где 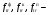 средние доли энергии от начальной энергии фотонов, передаваемые электронам при фотоэффекте, комптоновском рассеянии и эффекте образования пары электрон-позитрон соответственно. средние доли энергии от начальной энергии фотонов, передаваемые электронам при фотоэффекте, комптоновском рассеянии и эффекте образования пары электрон-позитрон соответственно.
Значение 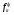 можно рассчитать по формуле можно рассчитать по формуле
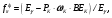 (1.80) (1.80)
где BEK – энергия связи электрона на K-оболочке; PK– доля фотоэлектрических взаимодействий, имеющих место на K-оболочке; ωK – выход характеристического излучения для K-оболочки. На практике нередко приближенно принимают 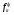 = =1. = =1.
Значение 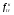 можно рассчитать из выражения (1.68) или по формуле можно рассчитать из выражения (1.68) или по формуле
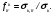 (1.81) (1.81)
Наконец для расчета 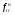 применяется уравнение применяется уравнение
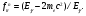 (1.82) (1.82)
Массовый коэффициент поглощения энергии применяется для расчете поглощенной дозы в условиях существования электронного равновесия. Соответствующая формула имеет вид
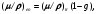 (1.83) (1.83)
где g– относительная доля энергии, идущая на образование электронами тормозного излучения.
|
 Скачать 9.62 Mb.
Скачать 9.62 Mb.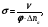 (1.37)
(1.37)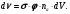 (1.38)
(1.38)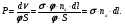 (1.39)
(1.39)
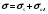 (1.40)
(1.40)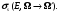

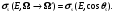 (1.41)
(1.41)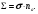 (1.41)
(1.41)

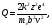 (1.42)
(1.42)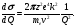 (1.43)
(1.43) 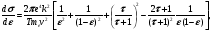 (1.44)
(1.44)
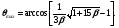 (1.48)
(1.48)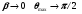 и при
и при 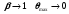 . Это указывает, что в диагностической радиологии (ортовольтовые пучки) большая часть рентгеновского излучения испускается под углом 90о по отношению к направлению падения пучка электронов на мишень, в то время как в мегавольтном диапазоне (линейные медицинские ускорители электронов (ЛУЭ)) угол максимальной интенсивности близок 0о.
. Это указывает, что в диагностической радиологии (ортовольтовые пучки) большая часть рентгеновского излучения испускается под углом 90о по отношению к направлению падения пучка электронов на мишень, в то время как в мегавольтном диапазоне (линейные медицинские ускорители электронов (ЛУЭ)) угол максимальной интенсивности близок 0о.
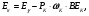 (1.65)
(1.65)
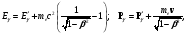 (1.66)
(1.66)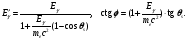 (1.67)
(1.67)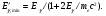 (1.68)
(1.68)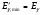 , т.е. потери энергии в результате комптоновского рассеяния незначительны.
, т.е. потери энергии в результате комптоновского рассеяния незначительны. 10-24 см2/электрон при очень низких энергиях до 0,051
10-24 см2/электрон при очень низких энергиях до 0,051 10-24 см2/электрон при Eγ = 10 МэВ (рис. 1.16).
10-24 см2/электрон при Eγ = 10 МэВ (рис. 1.16).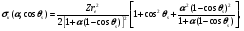

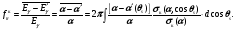 (1.70)
(1.70)
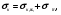 (1.71)
(1.71)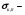 принято называть сечением передачи энергии при комптоновском взаимодействии;
принято называть сечением передачи энергии при комптоновском взаимодействии; 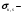 сечением рассеяния энергии при комптоновском взаимодействии. Эти величины определяются из следующих уравнений.
сечением рассеяния энергии при комптоновском взаимодействии. Эти величины определяются из следующих уравнений.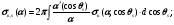 (1.72)
(1.72)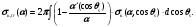 (1.73)
(1.73)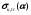 наблюдается пик, что связано с небольшими потерями энергии фотонами при их комптоновском взаимодействии в области малых энергий.
наблюдается пик, что связано с небольшими потерями энергии фотонами при их комптоновском взаимодействии в области малых энергий.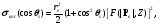 (1.74)
(1.74)
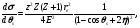 (1.45)
(1.45)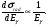 (1.46)
(1.46)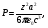 (1.47)
(1.47) 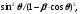 где θ – угол между ускорением заряженной частицы и единичным вектором, связывающим заряд и точку наблюдения; β – стандартное релятивистское отношение v/c. При небольших скоростях v заряженной частицы угловое распределение пропорционально sin2θ, т.е. имеет максимум при θ = 90о. Однако при увеличении скорости до
где θ – угол между ускорением заряженной частицы и единичным вектором, связывающим заряд и точку наблюдения; β – стандартное релятивистское отношение v/c. При небольших скоростях v заряженной частицы угловое распределение пропорционально sin2θ, т.е. имеет максимум при θ = 90о. Однако при увеличении скорости до 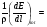 (S/ρ)tot= (S/ρ)col + (S/ρ)rad, (1.49)
(S/ρ)tot= (S/ρ)col + (S/ρ)rad, (1.49)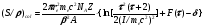 , (1.50)
, (1.50)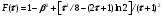 . (1.51)
. (1.51)
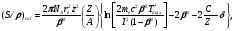
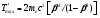 . Уравнение (1.52), следуя Аттиксу, можно упростить до следующего выражения:
. Уравнение (1.52), следуя Аттиксу, можно упростить до следующего выражения: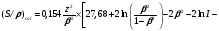
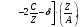 (1.53)
(1.53)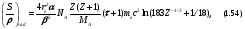 где α – постоянная тонкой структуры.
где α – постоянная тонкой структуры.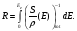 (1.55)
(1.55)
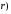 , исходя из знания пространственно-энергетического распределения флюенса электронов
, исходя из знания пространственно-энергетического распределения флюенса электронов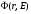 , использование понятия массовой тормозной способности будет некорректным. Для определения связи между этими двумя величинами вводится понятие ограниченной тормозной способности столкновений.
, использование понятия массовой тормозной способности будет некорректным. Для определения связи между этими двумя величинами вводится понятие ограниченной тормозной способности столкновений.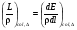 (1.56)
(1.56)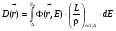 . (1.57)
. (1.57)
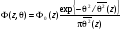 , (1.58)
, (1.58)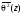 – средний квадрат углового расширения пучка;
– средний квадрат углового расширения пучка; 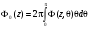 .
.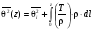 , (1.59)
, (1.59)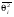 – начальное значение среднего квадрата углового расширения пучка.
– начальное значение среднего квадрата углового расширения пучка.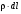 :
: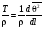 . (1.60)
. (1.60)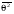 и глубиной проникновения пучка в достаточно широком интервале глубин [6,10]. С дальнейшим с увеличением глубины формируется равновесное угловое распределение, так как электроны, рассеянные на большие углы, быстро выбывают из пучка. Массовая угловая рассеивающая способность пропорциональна примерно квадрату атомного номера вещества и обратно пропорциональна кинетической энергии электрона.
и глубиной проникновения пучка в достаточно широком интервале глубин [6,10]. С дальнейшим с увеличением глубины формируется равновесное угловое распределение, так как электроны, рассеянные на большие углы, быстро выбывают из пучка. Массовая угловая рассеивающая способность пропорциональна примерно квадрату атомного номера вещества и обратно пропорциональна кинетической энергии электрона. 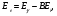 (1.61)
(1.61)
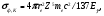 (1.62)
(1.62) 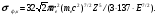 (1.63)
(1.63)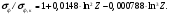 (1.64)
(1.64)
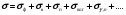 (1.75)
(1.75)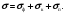 (1.76)
(1.76)
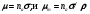 (1.77)
(1.77)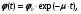 (1.78)
(1.78)
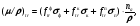 (1.79)
(1.79)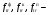 средние доли энергии от начальной энергии фотонов, передаваемые электронам при фотоэффекте, комптоновском рассеянии и эффекте образования пары электрон-позитрон соответственно.
средние доли энергии от начальной энергии фотонов, передаваемые электронам при фотоэффекте, комптоновском рассеянии и эффекте образования пары электрон-позитрон соответственно.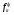 можно рассчитать по формуле
можно рассчитать по формуле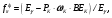 (1.80)
(1.80)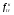 можно рассчитать из выражения (1.68) или по формуле
можно рассчитать из выражения (1.68) или по формуле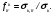 (1.81)
(1.81)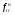 применяется уравнение
применяется уравнение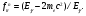 (1.82)
(1.82)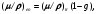 (1.83)
(1.83)