НСПК Практическая 2 матем. Формирование умений решать текстовые задачи применять математические методы для решения профессиональных задач закрепление навыков решения простейших статистических задач
 Скачать 244.86 Kb. Скачать 244.86 Kb.
|
|
Автономная некоммерческая профессиональная образовательная организация "Национальный социально-педагогический колледж" Программа среднего профессионального образования 44.02.01 Дошкольное образование Дисциплина: Математика Практическое занятие 2 Выполнил: Обучающийся ФИО Преподаватель: ФИО ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 2 Цель занятия: формирование умений решать текстовые задачи; применять математические методы для решения профессиональных задач; закрепление навыков решения простейших статистических задач; закрепление навыков применять правила приближенных вычислений; закрепление навыков работы с основными свойствами геометрических фигур на плоскости и в пространстве. Задание 1. (Максимальное количество баллов – 3 балла) Таблица – «Виды моделирования при решении текстовых задач» В таблице «Виды моделирования при решении текстовых задач» заполните позицию «Необходимо определить» в графе «Интерпретация модели».
Задание 2. (Максимальное количество баллов – 3 балла) Используя диаграммы Эйлера-Венна решить задачу. При выборе кружков для детей оказалось, что 60% родителей желают, чтобы их ребенок посещал кружок рисования, 50% предпочли занятия по гимнастике, 50% отметили, что выбрали бы занятия музыкой. При этом 30% родителей предпочитают, чтобы их дети посещали занятия и по рисованию, и по гимнастике, 20% – сделали выбор в пользу занятий по гимнастике и музыке, а 40% родителей – пожелали бы, чтобы ребенок рисовал и занимался хоровым пением, и только 10% из них выразили свое мнение за посещение детьми всех кружков. Определите процентное соотношение родителей, которые: 1) не желают водить детей в кружки; 2) выбрали не менее двух кружков. Решение: Составим диаграмму Эйлера-Венна и нанесем на нее известные нам данные. 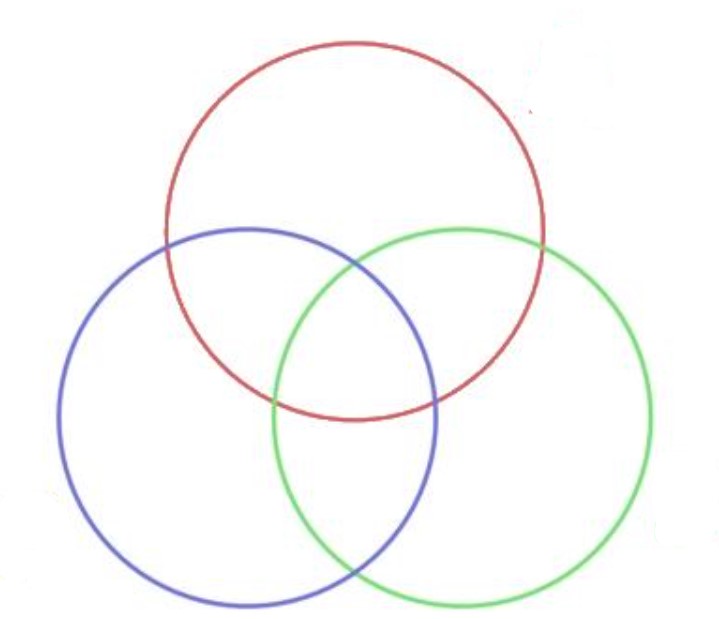 рисование гимнастика музыка 60% 50% 50% 20% 10% 30% 10% 10% 1) не желают водить детей в кружки – 0%; 2) выбрали не менее двух кружков – 20%+10%+30%+10%=70%. Задание 3 (максимальное количество баллов – 5 баллов) При измерении получены данные:
Выполните задания с учетом исходных данных, подробно описывая ход решения. a) Построить статистический ряд распределения частот. b) Построить полигон распределения. c) Вычислить выборочную среднюю, дисперсию, моду, медиану. d) Построить выборочную функцию распределения. Решение: a) Построить статистический ряд распределения частот. Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда. Таблица для расчета показателей.
b) Построить полигон распределения. 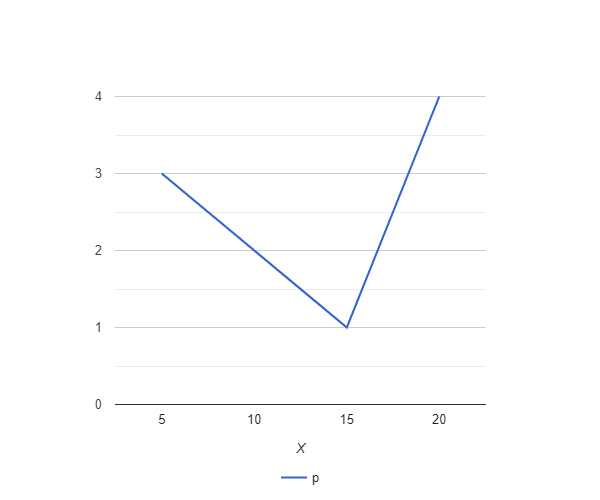 c) Вычислить выборочную среднюю, дисперсию, моду, медиану. Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Максимальное значение повторений при x = 20 (f = 4). Следовательно, мода равна 20. Медиана. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 6. Это значение xi =15 . Таким образом, медиана равна 15. Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных. Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 20 - 5 = 15 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 6 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 13 в среднем на 6,403 d) Построить выборочную функцию распределения.
Функция распределения F(X). F(x≤5) = 0 F(5< x ≤10) = 0,3 F(10< x ≤15) = 0,2 + 0,3 = 0,5 F(15< x ≤20) = 0,1 + 0,5 = 0,6 F(x>20) = 1 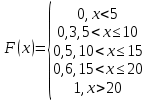 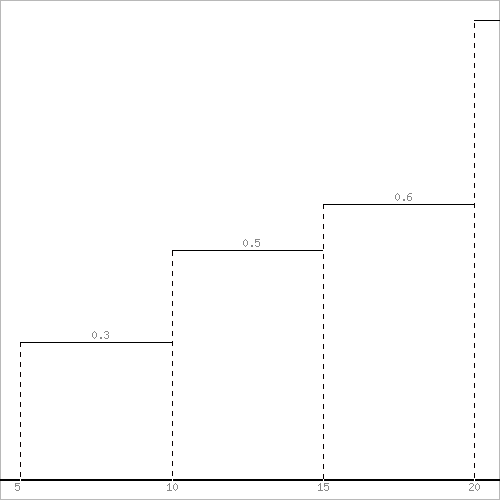 Задание 4 (максимальное количество баллов - 4 балла) Решите примеры, связанные с погрешностями, подробно описывая ход решения. Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями. Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление. Правила округления чисел: 1. Подчеркнуть цифру разряда, до которого надо округлить число. 2. Отделить все цифры справа от этого разряда вертикальной чертой. 3. Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений. 4. Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1. a) Округлить число 4,45575250 до шести, пяти, четырех, трех, двух и одного десятичных знаков; до целого числа. Решение: шести десятичных знаков 4,45575250≈4,455753 пояснение: шестой десятичный знак – цифра 2, справа от нее стоит цифра 5, следовательно к цифре 2 прибавляем 1. пяти десятичных знаков 4,45575250≈4,45575 пояснение: пятый десятичный знак – цифра 5, справа от нее стоит цифра 2, следовательно цифру 5 оставим без изменений. четырех десятичных знаков 4,45575250≈4,4558 пояснение: четвертый десятичный знак – цифра 7, справа от нее стоит цифра 5, следовательно к цифре 7 прибавляем 1. трех десятичных знаков 4,45575250≈4,456 пояснение: третий десятичный знак – цифра 5, справа от нее стоит цифра 7, следовательно к цифре 5 прибавляем 1 двух десятичных знаков 4,45575250≈4,46 пояснение: второй десятичный знак – цифра 5, справа от нее стоит цифра 5, следовательно к цифре 5 прибавляем 1 одного десятичного знака 4,45575250≈4,5 пояснение: первый десятичный знак – цифра 4, справа от нее стоит цифра 5, следовательно к цифре 4 прибавляем 1 до целого числа. 4,45575250≈4 пояснение: целое – цифра 4, справа от нее стоит цифра 4, следовательно цифру 4 оставим без изменений. b) Число 12,75 определено с относительной погрешностью 0,3, %. Найдите абсолютную погрешность округления. Решение: а- точное число не известно, 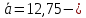 приближенное число приближенное числоδ=0,003 – относительная погрешность приближенного числа 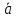 Δ – абсолютная погрешность округления (истинная). Погрешность мала, поэтому используем формулу: 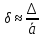 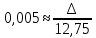 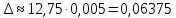 Ответ: 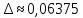 c) Определите верные и сомнительные цифры числа 13,27 ± 0,03. Решение: Незначащими цифрами числа называются нули в начале десятичных дробей, меньших 1, и нули в конце числа, заменившие цифры, отброшенные после округления. Остальные цифры называются значащими. Сомнительной цифрой результата измерения называется цифра, стоящая в разряде, соответствующем старшему разряду со значащей цифрой в значении погрешности. Цифры, стоящие слева от сомнительной называются верными, а справа – неверными. Таким образом, значащие верны цифры 13,2. Сомнительные - 7. Задание 5 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. На стороне AC треугольника ABC отмечена точка D так, что AD=3см, DC=10см. Площадь треугольника ABC равна 39 см2. Найдите площадь треугольника ABD. Решение: 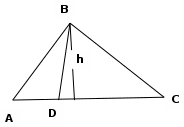 Проведем высоту из вершины B. Заметим, что это высота не только треугольника ABC, но и треугольника ABD. Найдем высоту, используя формулу площади треугольника для треугольника ABC: SABC=AC*h/2=(AD+DC)*h/2 39=(3+10)*h/2 39=13*h/2 39*2=13h h=6 см Теперь применим эту же формулу для треугольника ABD: SABD=AD*h/2=2*6/2=6 см2 Ответ: 6 см2. Задание 6 (максимальное количество баллов – 4 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Биссектриса угла A параллелограмма ABCD пересекает его сторону BC в точке F. Найдите площадь параллелограмма ABCD, если BF=4 см, FC=2 см, а угол ABC равен 1500. Решение: 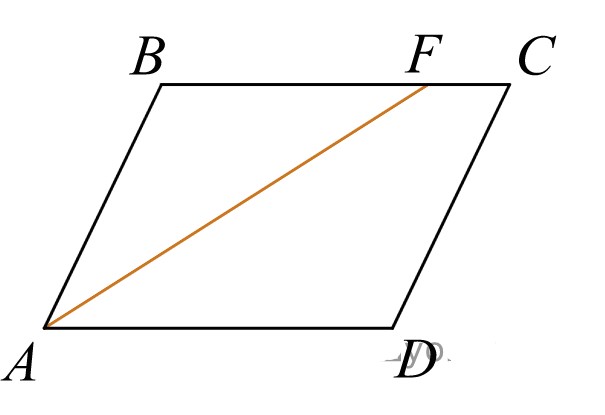 Накрест лежащие углы BFA и FAD равны, АF – биссектриса угла BAD, следовательно, 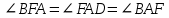 Значит треугольник BFA – равнобедренный и AB=BF=4 см. По формуле площади параллелограмма находим 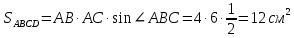 Ответ: 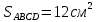 Задание 7 (максимальное количество баллов – 3 балла) Решите задачу, подробно описывая ход рассуждений. Решение сопроводите графическим отображением. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6см и 8см, а боковое ребро призмы равно 12см. Решение: 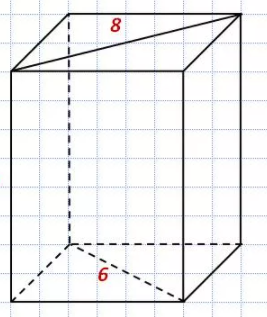 Сторона ромба a выражается через его диагонали 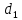 и и 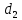 формулой формулой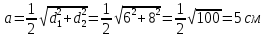 Находим площадь ромба 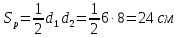 Тогда площадь поверхности призмы равна  Ответ:  Пермь - 2022 |







