Фотоприемные_устройства. Фотоприемные полупроводниковые устройства интегральной оптоэлектроники
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
|
Элементарная теория P-N перехода В диффузионно-дрейфовом приближении плотности электронного и дырочного токов записываются в виде:  (28) (28)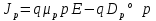 (29) (29) , (30) , (30)где J - полная плотность тока в полупроводниковой структуре, q – заряд электрона, E – напряженность электрического тока, µn – подвижность электронов, µp – подвижность дырок, Dn – коэффициент диффузии электронов, Dp – коэффициент диффузии дырок. Подвижности носителей заряда и их коэффициенты диффузии не являются независимыми величинами и связаны соотношением, которое известно как соотношение Эйнштейна:  . (31) . (31)В сильных электрических полях в уравнениях (28)-(29) следует заменить произведения µE (которые представляют собой средние скорости движения носителей заряда при наличии электрического поля E) на соответствующие скорости насыщения носителей заряда vнас. Для полупроводников, находящихся во внешних магнитных полях, в правой части уравнений (19)-(20) следует добавить слагаемые J┴ tg(θn) и J┴tg(θp) соответственно, где J┴ и J┴ – компоненты плотности электронного и дырочного тока, перпендикулярные магнитному полю, а tg(θn)=qµnnRHIHI (и аналогично для дырочной компоненты), где RH – коэффициент Холла. В свою очередь, компоненты плотностей тока присутствуют в уравнениях непрерывности, связывающих изменения плотности носителей заряда с плотностями их потоков с учетом процессов генерации и рекомбинации в объеме полупроводника:  (32) (32) , (33) , (33)где Gn и Gp – темп генерации электронов и дырок в единице объема (см-3/с), вызываемый внешними воздействиями, такими, как оптическое возбуждение или ударная ионизация в сильных полях. Скорость рекомбинации электронов в полупроводнике р-типа обозначена символом Un. При малых уровнях возбуждения, когда концентрация избыточных (по сравнению с равновесной концентрацией носителей заряда) мала, то темп рекомбинации можно записать в виде: Un≈(np-np0)/τn, где np – избыточная концентрация неосновных носителей тока, np0 термодинамическое равновесное значение этой величины, τ – время жизни неосновных носителей заряда (электронов). Аналогичным образом в полупроводнике n – типа скорость рекомбинации дырок определяется через дырочное время жизни τp. В одномерном случае, после подстановки выражений для плотности токов электронов и дырок (28)-(29) в (32)-33), имеем:  (34) (34) , (35) , (35)которые еще более упрощаются в стационарном случае, когда  . . (36) (36) . (37) . (37)Равновесные и неравновесные концентрации носителей заряда Идеализированные вольтамперные характеристики полупроводниковых устройств обычно вычисляются на основе следующих допущений: 1) приближения обедненного слоя с резкими границами, т.е. контактная разность потенциалов и приложенное напряжение уравновешены двойным заряженным слоем с резкими границами, вне которых полупроводник считается нейтральным; 2) приближения Больцмана, т.е. в обедненной области справедливы распределения Больцмана; 3) приближения низкого уровня инжекции, т.е. плотность избыточных носителей заряда мала по сравнению с концентрацией основных носителей. В состоянии теплового равновесия в приближении Больцмана концентрации равновесных электронов и дырок можно определить из следующих соотношений:  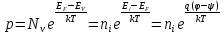 , (38) , (38)где Nc, Nv – эффективные плотности состояний зоны проводимости и валентной зоны, ni – собственная концентрация носителей заряда полупроводника, EF – уровень Ферми, Ei – энергетический уровень, соответствующий середине запрещенной зоны полупроводника, ψ и ϕ – потенциалы, соответствующие середине запрещенной зоны и уровню Ферми( ψ=-Ei/q, ϕ=-EF/q), к – постоянная Больцмана, Т – абсолютная температура. В состоянии теплового равновесия из (38) следует:  . (39) . (39)При подаче на переход напряжения смещения по обеим его сторонам происходит изменение концентрации неосновных носителей и произведение pn уже не может равняться ni2. В этом случае вводятся квазиуровни Ферми в соответствие со следующими соотношениями:  , (40) , (40)где ϕn и ϕp – квазиуровни Ферми для электронов и дырок. Из (27) следует, что 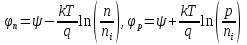 . (41) . (41)Тогда  . (42) . (42)При прямом смещении (ϕp-ϕn)>0 и pn>ni2, а при обратном (ϕp-ϕn)<0 и pn<ni2. Из выражения (28) и (41) с учетом того, что E=-��ψ, получим  . (43) . (43)Аналогично для дырочного тока имеем  . (44) . (44)Таким образом, плотности электронного тока и дырочного тока пропорциональны градиентам квазиуровней Ферми для электронов и дырок соответственно. Если ϕn=ϕp=ϕ=const в состоянии теплового равновесия, то Jn=Jp=0. В квазинейтральных областях pn-перехода, где напряженность электрического поля практически равна нулю, квазиуровни Ферми практически постоянны и основное их изменение осуществляется в области пространственного заряда (в обедненной области pn-перехода). Разность электрических потенциалов pn-перехода определяется величиной 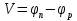 . (45) . (45)Учитывая (42), получаем концентрацию электронов на границе обедненного слоя в р-области перехода при x=-xp  , (46) , (46)где np0 – равновесная концентрация электронов в p-области. Аналогично  , (47) , (47)где np0 – равновесная концентрация электронов на границе обедненного слоя в p-области перехода при x=-xp, а pn0 – равновесная концентрация дырок в n-области.  Рис.7. Схематическое представление распределения концентраций неосновных носителей заряда вблизи границ обедненной области pn-перехода при прямом смещении (рис.(a)) и обратном (рис.(b)) и плотностей токов при прямом смещении (рис.(с)) и обратном (рис.(d)). При обратном смещении ширина области пространственного заряда увеличивается и, наоборот, при прямом смещении уменьшается. Полученные выражения (46)-(47) имеют собственное название как граничные условия Шокли и являются основными граничными условиями при вычислении вольтамперной характеристики pn-перехода. Контактная разность потенциалов Основные носители заряда при переходе через p и n области перехода должны преодолевать потенциальный барьер. В состоянии термодинамического равновесия диффузионный ток основных носителей заряда Jоp и Jоn уравновешен дрейфовым током неосновных носителей заряда Jнp и Jнn, и суммарный ток через pn-переход равен нулю. Если Φn есть работа выхода электронов из электронного полупроводника, а Φp – из дырочного, то величина потенциального барьера будет определяться выражением: 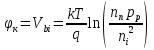 (48) (48)или  , (49) , (49)где Vbi – общепринятое обозначение контактной разности потенциалов, которое в случае pn-перехода имеет собственное название встроенный или диффузионный потенциал (built in potential). Т.о., контактная разность потенциалов на pn-переходе тем больше, чем сильнее легированы n- и p-области полупроводника. Из (49) в состоянии термодинамического равновесия непосредственно следует 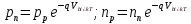 . (50) . (50)Пусть к переходу приложено внешнее напряжение V, минус – к электронному полупроводнику, а плюс – дырочному, т.е. к pn-переходу приложено напряжение в прямом смещении. Поскольку сопротивление слоя объемного заряда высокое, то падение напряжения в основном будет в этой области. Вследствие этого высота барьера снижается на величину qV по сравнению с равновесным состоянием. Понижение потенциального барьера приведет к увеличению потока основных носителей, т.к. большее число электронов из n-области будет переходить в p-область и большее число дырок из p-области в n-область, а поток неосновных носителей заряда останется практически неизменным. В результате во внешней цепи будет протекать ток, равный разности токов основных и неосновных носителей заряда и направленный от p-области к n-области, т.е. J=Jон-Jнн. В n-области, появившиеся избыточные неосновные носители заряда – дырки Δp создадут в первый момент вблизи контакта положительный объемный заряд, который за очень короткое время определяемое временем максвелловской релаксации будет скомпенсирован зарядом основных заряда – электронов, которые под действием электрического поля, созданного избыточными дырками, будут подтянуты в количестве Δn из глубины n-области, а в n-область избыточные электроны поступят из внешней цепи. Т.о., во всех частях электронного полупроводника будет соблюдаться электронейтральность, но в приконтактной области перехода концентрация будет повышена на величину Δn=Δp по сравнению с равновесным состоянием. Введение в полупроводник избыточных носителей заряда с помощью pn-перехода при подаче на него прямого смещения, где эти носители являются неосновными, называется инжекция носителей заряда. Соответственно,  , (51) , (51)откуда следует, что концентрация избыточных дырок в n-области при x=xn равна:  . (52) . (52)Совершенно аналогично 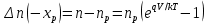 . (53) . (53)Если внешнее напряжение приложено в обратном направлении, т.е. плюс к электронному полупроводнику, потенциальный барьер повышается и увеличивается толщина области пространственного заряда. В этом случае из (38) следует, что при большом отрицательном V концентрация дырок при x=xn быстро стремиться к нулю. Аналогично, концентрация электронов при x=-xp также стремится к нулю. Такой режим работы pn-перехода называется режимом экстракции носителей заряда. При обратном включении pn-перехода ток основных носителей заряда будет меньше, чем при равновесном состоянии, а ток неосновных носителей практически не изменится. Поэтому суммарный ток через pn-переход будет направлен из n-области к p-области и с увеличением обратного напряжения стремится к некоторой величине, называемой током насыщения. Связь распределения электрического потенциала, концентрацией легирующей примеси и концентрациями свободных носителей заряда осуществляется в уравнении Пуассона, которое в одномерном случае имеет вид: 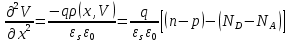 , (54) , (54)где ND(x), NA(x) – концентрации донорной и акцепторной примеси, n(x,V), p(x,V) – концентрации электронов и дырок, εs, ε0 – относительная диэлектрическая проницаемость полупроводника и диэлектрическая проницаемость вакуума (ε0=8.854·10-14 [ф/см]), ρ – пространственная плотность заряда, V – электростатический потенциал. Если принять, что при термодинамическом равновесии вся легирующая примесь является полностью ионизированной, то n≈(ND+-NA-) и p=ni2/n. В квазинейтральных областях pn-перехода (где область пространственного заряда отсутствует), поэтому  (55) (55)и  . (56) . (56)В случае резкого перехода концентрациями подвижных носителей заряда n и p в области пространственного заряда пренебрегают и уравнение Пуассона (54) приобретает вид: 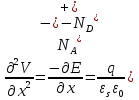 (57) (57)или 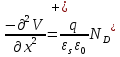 для для  (58) (58) для для 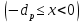 . (59) . (59) Рис.8. Обедненная область в случае резкого pn-перехода. Интегрируя (58)-(59) один раз, находим выражение для электрического поля 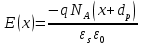 для для 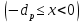 (60) (60) для для  , (61) , (61)где Em – максимальное значение электрического поля, которое достигается при x=0 и равно  . (62) . (62)Еще раз интегрируя уравнение Пуассона, получим распределение потенциала и величину диффузионного потенциала V(x): 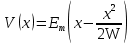 , (63) , (63) , (64) , (64)где W – ширина обедненной области. Исключая Em из (64) с использованием (62), получим для резкого pn-перехода в равновесном случае  . (65) . (65)В случае прямого смещения pn-перехода величина обедненной области уменьшается:  , (66) , (66)а в случае обратного смещения (-V) увеличивается:  . (67) . (67)Более точное выражение для ширины области пространственного заряда получается, если кроме концентрации ионизированной примеси дополнительно учесть вклад основных носителей заряда, т.е. положить ρ≈-q[NA-p(x)] в p-области перехода и ρ≈-q[ND-n(x)] в n-области перехода. Ширина обедненной области в таком приближении вычисляется по тем же формулам (53)-(54) если заменить Vbi на Vbi-2kT/q. Поправочный член появляется из-за наличия двух «хвостов» распределения основных носителей заряда. Каждый из них вносит поправку kT/q. Сама поправка представляет дипольный момент неточности в распределении, равной разности между истинным распределением и распределением в резком переходе. Соответственно, (66) и (67) переписываются в виде: 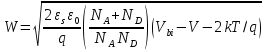 (68) (68) . (69) . (69) |
