Практикум. Г. А. Зверев Л. К. Митрюхин
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
|
Контрольные вопросы и задания Сформулируйте и запишите закон Ома для однородного, неоднородного участка и замкнутой цепи. От каких параметров зависит сопротивление проводника? Запишите и сформулируйте правила Кирхгофа. Выведите формулу для определения сопротивления методом мостика Уитстона. В чем заключаются преимущества измерения сопротивления методом мостика Уитстона? Назовите другие методы определения сопротивления. Выведите формулы для определения сопротивлений при их последовательном и параллельном соединениях. Объясните принцип действия экспериментальной установки. Перечислите основные источники ошибок измерений в данной работе. Литература 1. Гл.12. §97-98. С.178-180.2. Гл.18. §18.3. С.240-241. Гл.19. §19.1. С.248-251. 4. Гл.VI. §57-58. С.112-116. 5. P.41. С.223. 9. Гл.XVI. §154. С.198-206. 11. Ч. III. §69. С.34. Лабораторная работа 7 ИЗМЕРЕНИЕ БОЛЬШИХ СОПРОТИВЛЕНИЙ С ПОМОЩЬЮ ТЛЕЮЩЕГО РАЗРЯДА В НЕОНОВОЙ ЛАМПЕ Приборы и принадлежности: неоновая лампа, конденсатор, измеряемое сопротивление, потенциометр, вольтметр, секундомер и источник тока ВУП-2. Цель работы: ознакомление с возникновениями релаксационных колебаний в RC цепочках, а также измерение больших сопротивлений с помощью тлеющего разряда. Теоретическое введение Под действием напряжения, наложенного на электроды неоновой лампы, находящийся в ней газ начинает светиться. Механизм этого свечения может быть описан так. Всегда имеющиеся в разрядном промежутке в небольшом количестве электроны разгоняются полем, существующим между электродами, и при встрече с нейтральными атомами либо ионизируют, либо «возбуждают» их. Последнее означает, что в нейтральном атоме под действием внешнего толчка наиболее слабо связанный с ядром электрон изменяет в атоме своё положение относительно ядра, отдаляясь от него. Через очень краткий промежуток времени возбуждённый атом переходит в нормальное состояние, испуская свет определённой длины волны. Процесс ионизации происходит лавинным образом. Это означает, что возникшие при ионизации электроны в свою очередь ионизируют нейтральные атомы вследствие чего лавинообразно нарастает число электронов и ионов в разрядном промежутке. Появление в результате такой ионизации большого количества ионов и электронов вызывает определённое распределение поля и потенциала в разрядном промежутке, характерное для того и иного типа разряда. Д 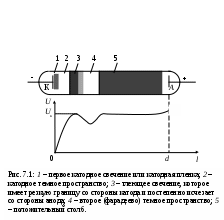  ля тлеющего разряда характерно то, что почти всё напряжение между электродами падает на узкую тёмную область, примыкающую к катоду. Весь остальной промежуток между электродами имеет потенциал, близкий к потенциалу анода (рис. 7.1). Такое распределение потенциала благоприятствует процессу ионизации, а положительные ионы накапливают энергию, необходимую для выбивания электронов из катода, пополняя запас электронов. До возникновения такого распределения потенциала иону и электрону необходимо пройти большой путь для накопления нужной энергии и, следовательно, заметная часть атомов разрядного промежутка не используется для ионизации. Этот неблагоприятный для разряда фактор компенсируется большим напряжением на электродах, что позволяет электрону и иону накопить нужную энергию на меньшем отрезке своего пути. В горящей лампе такое распределение потенциала уже создано, и можно без ущерба для устойчивости горения лампы уменьшить внешнее напряжение, подаваемое на электроды лампы. Таким образом, то напряжение на электроды лампы, при котором она зажигается (потенциал зажигания Uз), должно заметно отличаться от того, при котором она гаснет (потенциал гашения Uг). Различие в потенциалах зажигания и гашения лампы тлеющего разряда может быть использовано для получения в цепи лампы электрических колебаний, носящих название релаксационных колебаний. Р 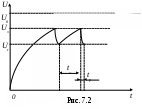 елаксационные коле-бания представляют со-бой незатухающие элек-трические колебания, форма которых харак-теризуется скачкообраз-ным изменением тока или напряжения (рис. 7.2). елаксационные коле-бания представляют со-бой незатухающие элек-трические колебания, форма которых харак-теризуется скачкообраз-ным изменением тока или напряжения (рис. 7.2).Электрическая цепь, в которой можно получить релаксацион-ные колебания, изображена на рис. 7.3, где обозначено: R – сопротивление порядка нескольких МОм, С – конденсатор, НL – неоновая лампа, V – вольтметр, ВУП-2М – источник постоянного напряжения. Под действием приложенного постоянного напряжения конденсатор будет заряжаться. Когда напряжение на конденсаторе становится равным потенциалу зажигания, неоновая лампа загорается. С 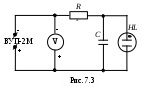 опротивление горящей лампы мало в сравнении с сопротивлением R, вследствие чего уход зарядов с обкладок конденсатора при раз-ряде через лампу не будет компенсироваться их приходом от источ-ника напряжения через сопротивление R. Напряжение на конденсаторе будет падать и, когда оно достигнет потенциала гашения лампы Uгаш, лампа гаснет. Разряд через лампу прекращается, конденсатор вновь заряжается, и таким образом возникает периодический процесс. опротивление горящей лампы мало в сравнении с сопротивлением R, вследствие чего уход зарядов с обкладок конденсатора при раз-ряде через лампу не будет компенсироваться их приходом от источ-ника напряжения через сопротивление R. Напряжение на конденсаторе будет падать и, когда оно достигнет потенциала гашения лампы Uгаш, лампа гаснет. Разряд через лампу прекращается, конденсатор вновь заряжается, и таким образом возникает периодический процесс.В любой момент времени имеем для напряжения на конденсаторе где I – сила протекающего в контуре тока. Так как отсюда имеем Пусть при t=0, Uc=Uг, тогда Периодом релаксационных колебаний называют время между двумя вспышками лампы. Так как время разряда конденсатора мало по сравнению со временем его заряда, можно за период релаксационных колебаний приближённо принять продолжительность зарядки конденсатора. Тогда при tз=T, Uc=Uз мы имеем Отсюда и 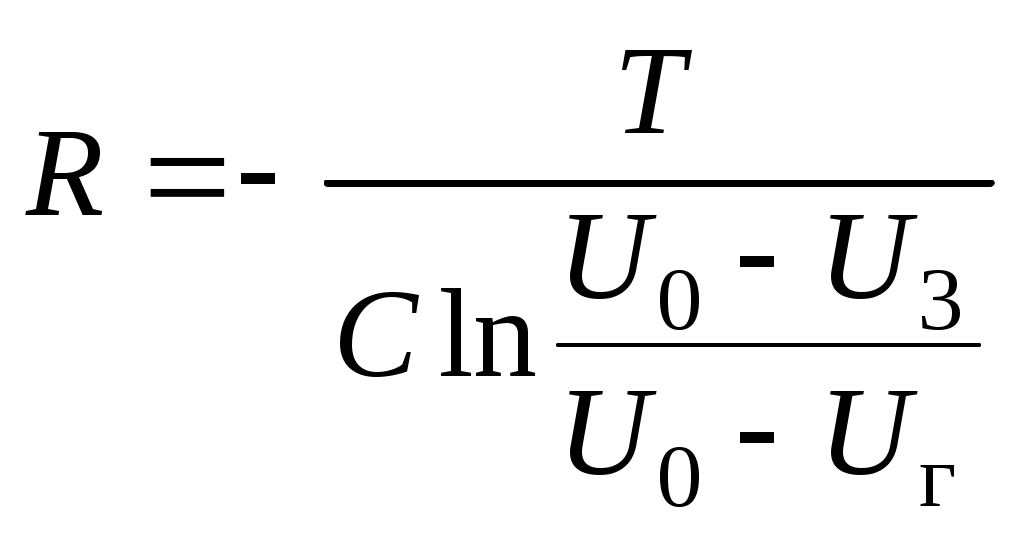 . (4) . (4)Описание экспериментальной установки и методики измерений 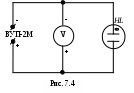 Схема (рис. 7.3) служит для определения периода релаксационных колебаний Т по числу вспышек за определённое время. В качестве нео-новой лампы используют тиратрон, в котором нап-ряжения зажигания и гашения определяются по схеме (рис. 7.4). Зная ёмкость конденсатора С, подаваемое напряжение U0, напряжение зажигания Uз, напряжение гашения Uг и период релаксационных колебаний Т, можно по формуле (4) найти искомое сопротивление R. Схема (рис. 7.3) служит для определения периода релаксационных колебаний Т по числу вспышек за определённое время. В качестве нео-новой лампы используют тиратрон, в котором нап-ряжения зажигания и гашения определяются по схеме (рис. 7.4). Зная ёмкость конденсатора С, подаваемое напряжение U0, напряжение зажигания Uз, напряжение гашения Uг и период релаксационных колебаний Т, можно по формуле (4) найти искомое сопротивление R.Порядок выполнения работы Собрать схему (рис. 7.4) для измерения Uз и Uг. Меняя напряжение на лампе, измерить вольтметром напряжения, соответствующие моментам зажигания и гашения неоновой лампы. Измерения надо произвести 5 раз. Собрать схему генератора релаксационных колебаний (рис. 7.3) и определить период Т. Для этого нужно за некоторый промежуток времени, измеряемый секундомером (например, за 2 минуты), сосчитать число вспышек n неоновой лампы при U0 Uз . Измерить U0. Обработка результатов измерений Результаты измерений занести в таблицы. По формуле (4) вычислить искомое сопротивление R.
Контрольные вопросы и задания Какой процесс называется релаксационным? Где находят применение релаксационные генераторы? Объясните принцип измерения больших сопротивлений и ёмкостей с помощью неоновой лампы. Почему потенциал гашения отличается от потенциала зажигания? Какие виды разрядов в газах вы знаете? Объясните механизм тлеющего разряда. Где находит применение тлеющий разряд? Каков механизм свечения неоновой лампы? Какие условия могут препятствовать измерению сопротивлений описанным методом? Литература 1. Гл.13. §106-108. С.194-202.2. Гл.20. §20.3-20.9. С.260-271. 4. Гл.ХVI. §166-170. С.358-364. 9. Гл.XVII. §169. С.266. 10. Гл.II. §14. С.304. ЛАБОРАТОРНАЯ РАБОТА 8 ИЗМЕРЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ КАТУШКИ Приборы и принадлежности: магнит, подвешенный на нити; катушка из медной проволоки; реостат; переключатель; источник постоянного напряжения. Цель работы: экспериментальное определение индукции магнитного поля, создаваемого внутри соленоида, по которому протекают различные токи. В качестве «индикатора» магнитного поля применяется постоянный магнит (магнитная стрелка), подвешенный на нити. Теоретическое введение В большинстве учебной литературы по курсу общей физики для технических факультетов в качестве силовой характеристики магнитного поля выбирается вектор магнитной индукции где Fmax – сила, с которой магнитное поле действует на элемент длины l с током I, внесенный в данную область поля. Из формулы (1) следует, что индукция магнитного поля численно равна максимальной силе Fmax, с которой магнитное поле действует на единичный элемент длины проводника с единичным током. Если в качестве «индикатора» магнитного поля взять маленькую рамку площадью S, по которой течет ток I , то индукция магнитного поля В может быть определена по формуле: где S – площадка, охватываемая контуром; Мmax – максимальный вращающий момент силы, действующий на рамку с током. Из формулы (2) определяем физический смысл индукции магнитного поля: индукция магнитного поля численно равна максимальному вращающему моменту силы, действующему на рамку единичной площади, по которой проходит единичный ток. Несложно показать, что формулы (1) и (2) идентичны друг другу. В зависимости от выбора «индикатора» магнитного поля возможны и другие способы определения вектора 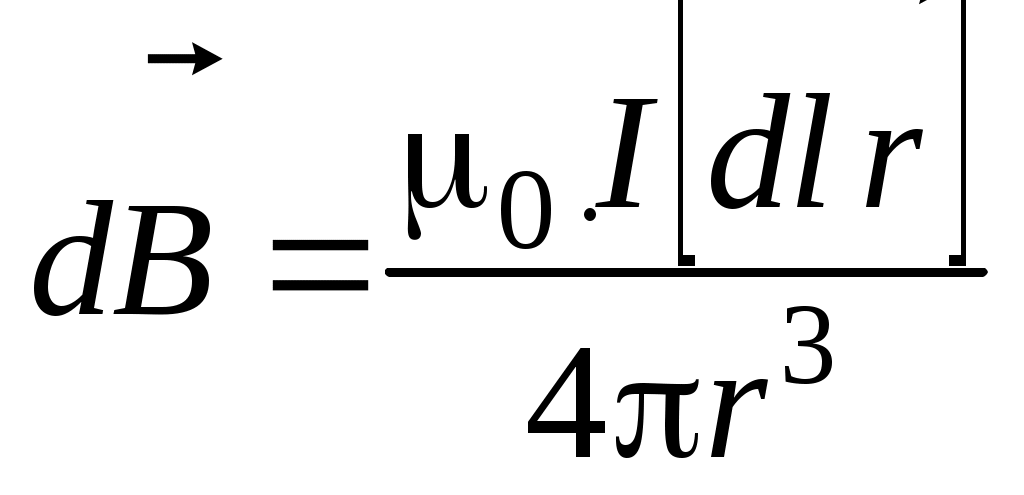 , (3) , (3)где 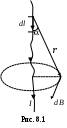 , (4) , (4)где В общем случае вращающий момент, действующий на рамку с током или магнитную стрелку, равен где Рm=IS–магнитный момент контура с током; – угол между направлениями векторов Приведенное определение используется и для постоянного магнита, который обладает остаточным магнитным моментом, определяемым геометрической суммой магнитных моментов его элементарных токов, имеющих упорядоченную ориентировку, т.е. где i – величина молекулярного тока вещества; S – площадка, охватываемая этим током. Если постоянный магнит, подвешенный на нити так, чтобы он мог вращаться около вертикальной оси, проходящей через центр тяжести, поместить в магнитное поле, то магнит устанавливается вдоль горизонтальной составляющей поля (рис. 8.2). В этом случае н 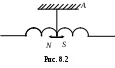 аправление магнитного момента магнита аправление магнитного момента магнита где К – момент инерции магнита, а так как при этих условиях то Эта формула используется в работе для определения индукции магнитного поля катушки при обтекании ее электрическим током. Примечание: формула (8) справедлива при условии, что упругостью нити подвеса можно пренебречь, т.е. 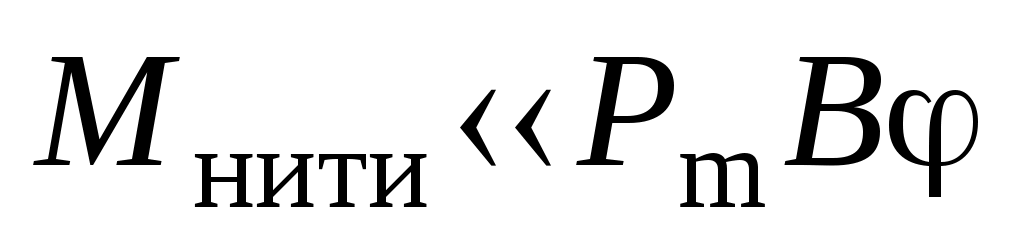 . .Вывод формулы (8) По основному уравнению динамики вращательного движения 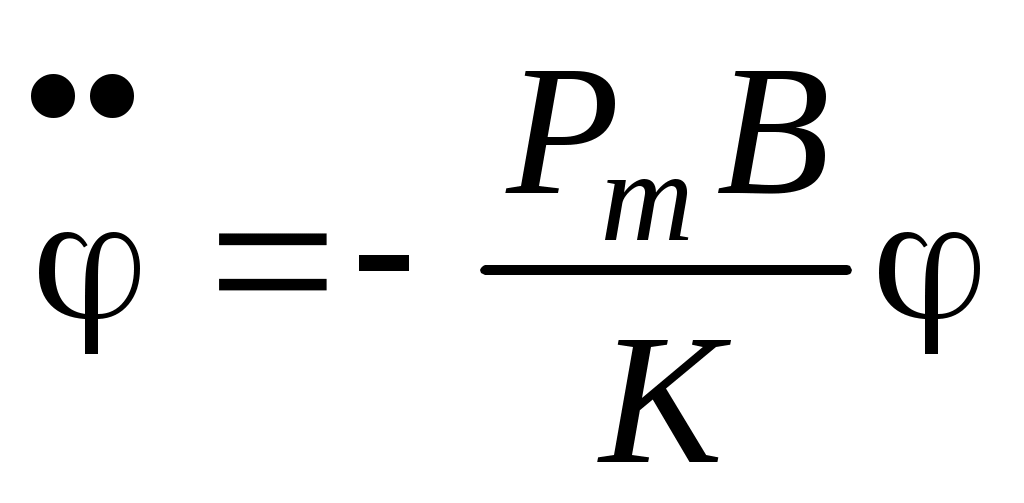 . .Так как обозначим Решение этого дифференциального уравнения имеет вид где Из формул (9) и (10) находим период колебания магнитной стрелки | ||||||||||||||||||||||||||||||||||||||||||
