Практикум. Г. А. Зверев Л. К. Митрюхин

• Название: Г. А. Зверев Л. К. Митрюхин
• Анкор: Практикум
• Дата: 29.09.2020
• Размер: 1.62 Mb.
• Имя файла: Laboratorny_praktikum_1.doc
• Тип: Практикум; #140063
• страница: 7 из 11

Описание аппаратуры и методики измерений

Как следует из формулы (8), для определения индукции магнитного поля необходимо знать Р_m, К и измерить период колебания маятника. В таком случае индукция магнитного поля определяется так

(11)

или

, (12)

где – величина, постоянная для данного магнита.

В этой работе величина  не рассчитывается, а определяется опытным путем на основании дополнительных измерений периода колебания магнита Т₀ в поле, индукция которого известна. Таким магнитным полем является поле Земли, горизонтальная составляющая магнитной индукции которого для Москвы В₀ = 1,8·10^-5 Тл. Таким образом, зная Т₀ и В₀, по формуле (12) найдем

. (13)

Для измерения индукции магнитного поля катушки магнит,

п одвешенный на нити, помещают в катушку (рис. 8.3). При включении напряжения по виткам катушки протекает ток и создается магнитное поле. Но в этом случае на магнитное поле тока в катушке накладывается магнитное поле Земли. Таким образом, период колебания магнита зависит уже от результирующего поля. Располагают ось катушки по магнитному меридиану и наблюдают колебания магнита NS в двух случаях: а) когда поле катушки и горизонтальная составляющая поля Земли совпадают по направлению; б) когда они направлены навстречу друг другу. Такое изменение направления поля осуществляется изменением направления тока в катушке. В первом случае имеем при условии

,

во втором случае

,

где Т₁ и Т₂ – соответствующие периоды колебаний; В – измеряемая индукция поля катушки.

Складывая эти соотношения, получаем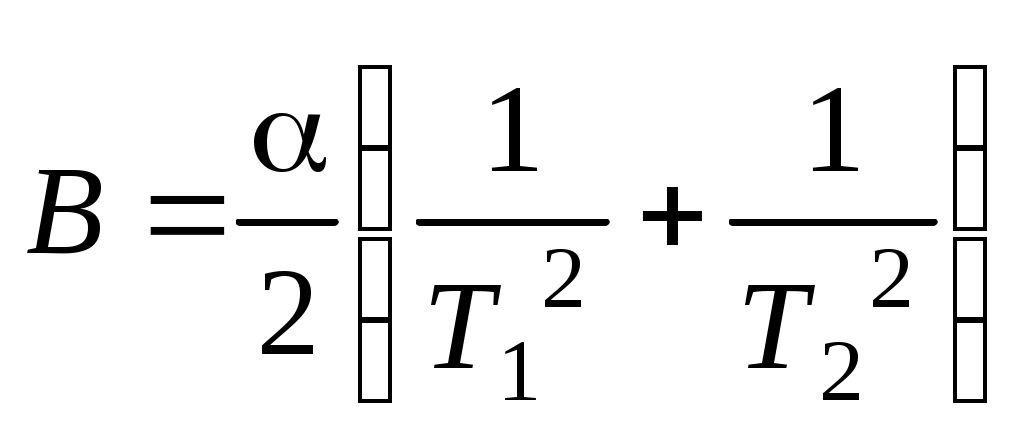

. (14)

Следовательно, измерение индукции поля катушки при известном  сводится к измерениям периодов Т₁ и Т₂.

Примечание: при условии уравнения будут иметь вид

;

.

Вычитая из одного другое, получим: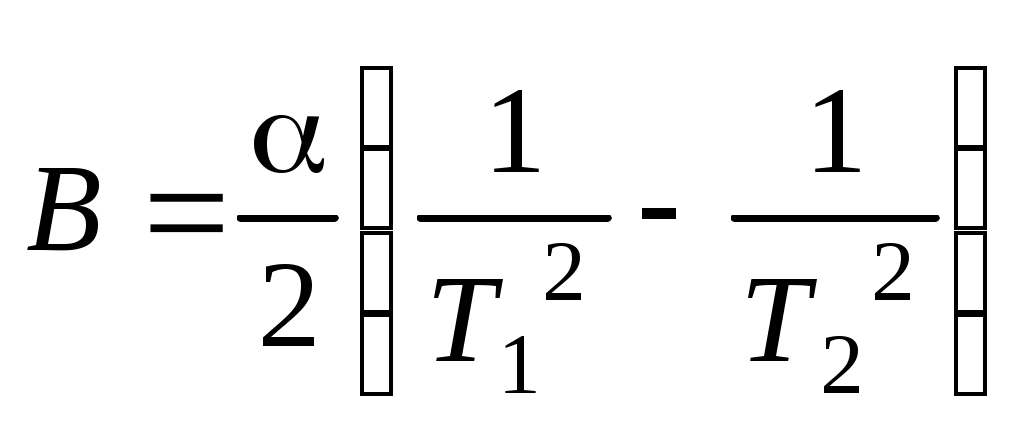

.
Порядок выполнения работы

1. 
   Собрать цепь по схеме (рис. 8.3), где L – катушка, NS – магнитная стрелка, П – переключатель, mА – миллиамперметр, R – реостат, В-24м – источник тока.
   
2. 
   Магнит, подвешенный на нити, поместить в центре катушки и с помощью его определить направление магнитного меридиана.
   
3. 
   Установить катушку так, чтобы ось ее совпадала с направлением магнитного меридиана, при этом магнит должен располагаться вдоль оси катушки.
   
4. 
   Поворотом относительно вертикальной оси на угол 4-6^о магнит вывести из состояния покоя. Измерить по секундомеру время t₀, за которое магнит совершит n крутильных колебаний (например, 20), записать время t₀ всех n колебаний.
   
5. 
   Включить напряжение и при помощи реостата установить необходимую силу тока I. При этих условиях произвести опыт так же, как указано в п.4, измеряя при этом время t₁.
   
6. 
   Так же измерить время крутильных колебаний при пяти других значениях тока, указанных преподавателем.
   
7. 
   С помощью переключателя П поменять направление тока в катушке и вновь повторить п. 5 и 6, измеряя время t₂.
   

Обработка результатов опыта и вычисление погрешности

По результатам измерений (п. 4) определить период Т₀ колебаний магнита в поле Земли, рассчитывая его по формуле

, (15)

а затем рассчитать постоянную  по формуле (13). Определить Т₁ и Т₂, которые соответственно равны 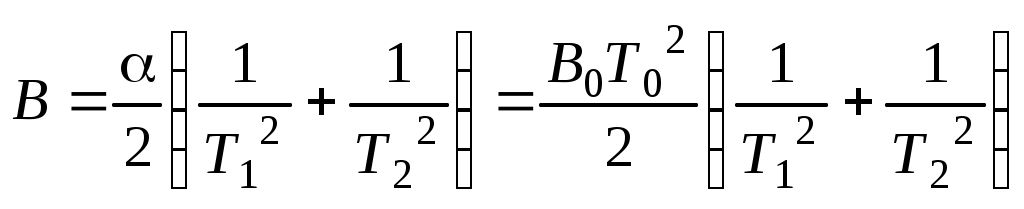, а затем по формуле (14) рассчитать индукцию поля катушки для каждого значения тока. По результатам опыта построить график В=f(I) и рассчитать относительную погрешность измерения при наибольшем значении тока. Для расчета погрешности измерений индукции используется выражение:

,

откуда следует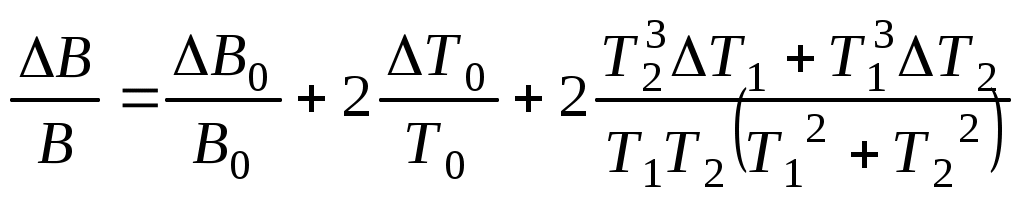

.
Протокол наблюдений и результаты измерений

Определение постоянной 

Номер измер.	t0, с	n	t0, с	t0cp, с	, Тл·с2
1
2
3
4
5

Определение В

Номер измер.	I, А	n1	t1, с	n2	t2, с	t1, с	t2, с	b, Тл
1
2
3
4
5

Контрольные вопросы и задания

1. 
   Объяснить закон Био–Савара–Лапласа.
   
2. 
   Как определить направление магнитного момента постоянного магнита?
   
3. 
   Почему график В=f(I), полученный в работе, отличается от
   

теоретического? Должен ли график В=f(I) пройти через 0? Почему?

4. 
   Влияет ли на точность эксперимента наличие вблизи установки приборов электромагнитной, магнитоэлектрической систем?
   
5. 
   Как рассчитать индукцию поля на оси соленоида и на концах?
   
6. 
   Какую погрешность вносит в результаты измерения собственная упругость нити?
   
7. 
   Какие поля действуют на магнитную стрелку?
   
8. 
   Почему надо менять направление тока в катушке?
   
9. 
   При каком условии положение рамки с током в магнитном поле будет наиболее устойчивым?
   
10. 
    Назовите основные методы, с помощью которых можно определить направление линий магнитной индукции.
    

Литература

1. Гл.14. §109-110. С.202-206. §119. С.215-217. 2. Гл.21. §21.3. С.276-281. Гл.22. §22.2. С.285-289. 3. Гл.VI. §42. С.114. 8. Гл.I. §1.1-1.4. С.4-11.

ЛАБОРАТОРНАЯ РАБОТА 9
ОПРЕДЕЛЕНИЕ МАГНИТНОЙ ИНДУКЦИИ
Приборы и принадлежности: короткая и длинная катушки, источник тока ВС-24м, амперметр и миллиамперметр переменного тока, цифровой вольтметр переменного тока.

Цель работы: изучение магнитных полей, создаваемых длинной и короткой катушками. Определение с помощью измерительного элемента (датчика) магнитной индукции на оси катушек и ее сравнение с величиной, полученной теоретически.
Теоретическое введение

Примерная картина магнитного поля короткой и длинной катушек показана на рис. 9.1,а и 9.2,а.
З 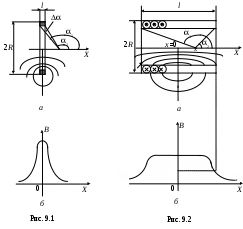начение магнитной индукции на оси катушки рассчитывается по формуле

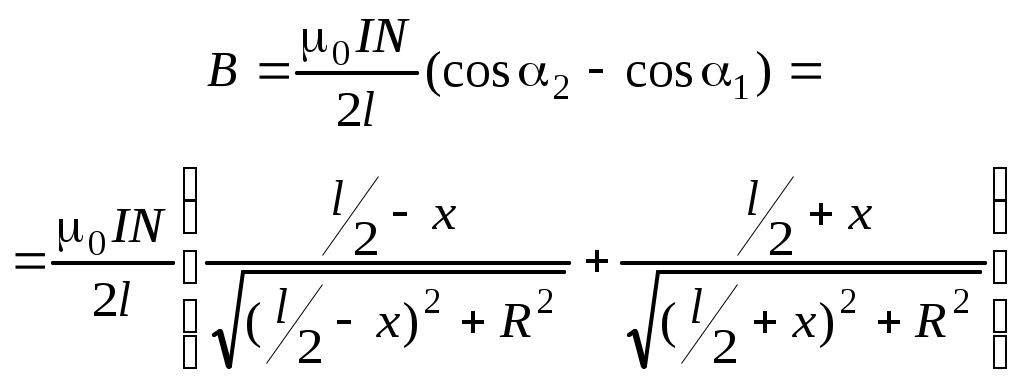, (1)

где N – число витков катушки; l – длина катушки; I – ток, протекающий по катушке; ₁ и ₂ – углы между направлением оси X и радиус-векторами, проведенными из точки на оси к краям катушки; х – координата точки на оси катушки, где определяется величина магнитной индукции (рис. 9.1), R – радиус катушки.

Если выполняется соотношение 2Rl (такую катушку называют соленоидом), то ₁0, а ₂. В этом случае для расчета величины магнитной индукции на оси катушки в центре и в торце из (1) получим

, (2)

, (3)

где – число витков на единицу длины соленоида.

Если выполняется соотношение l2R, то ;



; (4)

cos 1; sin  ;

(5)

Таким образом, подставив (4) в (1), с учетом (5) получим

, (6)

где N_к – число витков короткой катушки.

Формула (6) совпадает с формулой для расчета магнитной индукции на оси витка с током ВIN_к, которую можно получить, применив закон Био–Савара–Лапласа.
Описание установки и методики измерений

В качестве датчика магнитной индукции используется измерительная рамка, размещенная внутри соленоида на его оси. Так как ток в катушке меняется по гармоническому закону, то магнитная индукция в любой точке изменяется во времени по тому же закону , где В₀ – амплитудное значение, – циклическая частота.

Рамка размещается так, что плоскость ее витков перпендикулярна линиям индукции. Радиус рамки r_pR, поэтому поле в пределах рамки можно считать однородным в каждый момент времени. Магнитный поток через площадь рамки будет .

По закону электромагнитной индукции Фарадея–Максвелла в рамке индуцируется ЭДС

,

где N_p – число витков рамки.

Учитывая закон изменения магнитной индукции во времени, получим

.

Таким образом, магнитная индукция однозначно связана с ЭДС, возникающей в рамке

. (7)

Помещая измерительную рамку в разные точки на оси катушки и измеряя величину возникающей ЭДС индукции, можно получить распределение магнитной индукции.

Для удобства перемещения и отсчета координаты рамка закреплена на жестком штоке, снабженном сантиметровыми делениями. Через тот же шток выведен шнур, с помощью которого измерительная рамка подключается к милливольтметру.
Порядок выполнения работы

Определение магнитной индукции на оси короткой катушки

1. 
   Собрать схему по рис. 9.3.
   
2. 
   Включить сеть ВС-24, тумблер «СЕТЬ» милливольтметра и установить ток I< 2А.
   
3. 
   С помощью штока установить рамку так, чтобы вне катушки находилось два деления шкалы, нанесенной на шток. Перемещая рамку, добиться максимального показания милливольтметра, присоединенного к рамке. В этом положении рамка оказывается центре катушки (х=0).
   
4. 
   Перемещая шток каждый раз на 0,5 см, снять зависимость _х(х) охватив не менее пятнадцати точек.
   
5. 
   Результаты записать в табл. 9.1.
   
6.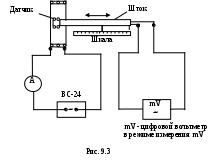 
   П о формуле (7) рассчитать значение магнитной индукции на оси короткой катушки для каждого значения координаты и построить график В_{к. эксп}=f(х).
   
7. 
   По известной методике рассчитать погрешность В_{к. эксп} для одного из значений координаты х и записать результат в стандартном виде.
   

Таблица 9.1

Определение магнитной индукции на оси короткой катушки

I_к < 2 А

х, см	, мВ	Вк. эксп, Тл	Вк. теор, Тл
0 0,5 1,0 1,5 2,0 … -0,5 -1,0 -1,5 …

Исследование зависимости магнитной индукции от силы тока

1. 
   Установить датчик в центре короткой катушки.
   
2. 
   Подключить короткую катушку к лицевой панели модуля.
   
3. 
   Снять зависимость ЭДС индукции  датчика от силы тока.
   
4. 
   Изменить положение датчика на оси катушки и проделать те же измерения что и в п.3.
   
5. 
   Результаты измерений записать в табл. 9.2.
   

Таблица 9.2

Исследование зависимости магнитной индукции

катушки от силы тока

Датчик в центре катушки х=0, см					Датчик в точке с координатой х= 2 см
Номер измер.	Iк, А	, мВ	Вк. эксп, Тл	Вк. теор, Тл	Iк, А	, мВ	Вк. эксп, Тл	Вк. теор, Тл
1. 2. 3. 4. 5.

1. По формуле (7) рассчитать величину магнитной индукции В_{к. эксп} для двух координат и построить зависимости В_{к. эксп} = f(I_к).

2. По формуле (6) рассчитать теоретическое значение В_{к. теор} для обеих точек и нанести результаты на те же графики.
Данные установки для короткой катушки

Nk = 640 витков lk = 2,5 cм Rk = 4 cм

Sp = 1 см2 = 1·10-4 м2 Np = 3135 витков  = 314 рад/с

Определение магнитной индукции на оси соленоида

Значение тока соленоида не изменяется, I_c < 500 mА.

1. 
   Собрать электрическую цепь по рис. 9.4, включить ВС-24 в сеть.
   
2. 
   Установить ток, идущий по соленоиду, I_c < 500 mА.
   
3. 
   Перемещая шток каждый раз на 1 см, снять зависимость ЭДС индукции  датчика от координаты х, получив не менее 40 точек. Результаты измерений занести в табл. 9.3.
   
4.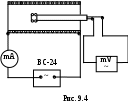 
   П о формуле (7) рассчитать значение магнитной индукции на оси соленоида для каждого значения координаты и построить график В_{с. эксп} =f(х). По известной методике рассчитать погрешность В_{с. эксп} для одного из значений координаты и записать результат в стандартном виде.
   
5. 
   Рассчитать теоретически магнитную индукцию на оси соленоида в центре и торце по формулам (2) и (3).
   

Таблица 9.3

х, см	, мВ	Вс. эксп, Тл	Вс. теор, Тл
0 1 2 . . . 45

Данные установки для соленоидов

1 соленоид Nc = 3000 витков lc = 41 см Rc = 4 см Sp = 0,6 см2 Np = 580 витков  = 314 рад/с

2 соленоид Nc = 4270 витков lc = 41 см Rc = 4 см Sp = 0,6 см2 Np = 580 витков  = 314 рад/с