Практикум. Г. А. Зверев Л. К. Митрюхин
 Скачать 1.62 Mb.
|
|
Контрольные вопросы и задания Из каких блоков состоит электронный осциллограф? Опишите устройство электронно-лучевой трубки. Что называется чувствительностью осциллографа? Объясните принцип работы генератора пилообразного напряжения. Что такое синхронизация сигналов и как она осуществляется в осциллографе? Как осуществляется развертка сигнала во времени на экране электронного осциллографа? Что такое фигуры Лиссажу и как их получают в данной работе? Для каких целей может быть использован осциллограф в научно-технических исследованиях? Как с помощью осциллографа можно измерить амплитуду и частоту исследуемого сигнала? Литература 1. Гл.13. §105. С.191-193. Гл.14. §114-115. С.209-210. 2. Гл.23. § 23.3. С.301-303. Гл.27. § 27.4. С364-369. 3. Р.49. С.259. 11. ч. III. §109. С.281. Лабораторная работа 4 Определение емкости конденсатора методом периодической зарядки и разрядки Приборы и принадлежности: автоматический переключатель PП-5, вольтметр, два конденсатора, реостат, источник напряжения постоянного тока и микроамперметр. Цель работы: определение емкостей отдельных конденсаторов и их емкостей при последовательном и параллельном соединениях по измерению токов зарядки и разрядки. Сравнение экспериментально полученных значений емкостей батарей конденсаторов с теоретическими. Теоретическое введение   Если заряженный конденсатор разрядить через баллистический гальванометр (см. описание гальванометра), то по первому отклонению его подвижной системы можно определить величину заряда конденсатора. Но если разряд осуществить через гальванометр с малым моментом инерции подвижной системы, то заряд можно определить лишь в случае, когда известна величина тока в гальванометре для всех моментов времени разряда. Тогда, учитывая, что  , получим  откуда,  что соответствует площади, указанной на рис. 4.1. Периодически заряжая и разряжая конденсатор через обычный гальванометр-микроамперметр, обладающий периодом колебаний во много раз больше, чем время разряда конденсатора, получаем отклоне-ние микроамперметра, не изменяя-ющееся со временем (постоянное отклонение). Это отклонение соответствует току I0, представ-ляющему его среднее значение за время, пока идет процесс пере-зарядки конденсатора (рис. 4.2).Так как I0 численно равно количеству электричества, протекающему через микроамперметр за 1с, протекающий заряд будет равен  , где  – заряд конденсатора,  – число разрядов за то же время. Выражая через емкость конденсатора С и напряжение U, получим  ;  или  , (1)где  – число разрядов за 1 с, f = 50 Гц. Полученное соотношение может быть использовано для определения одной из величин, входящих в него. В этой работе оно применяется для определения неизвестных емкостей двух конденсаторов и емкости при их параллельном и последовательном соединении.Описание аппаратуры и методики измерений  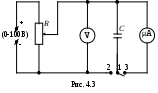 Исследуемый конденсатор (рис. 4.3) заряжается от источника ЭДС, а затем автоматически действующий переключатель отсоединяет одну из обкладок конденсатора от источника и замыкает на микро-амперметр. При этом конденсатор разряжается. Цикл зарядка–разрядка повторяется с частотой работы переключателя 50 раз в секунду. Сопротивление микроамперметра и емкость конденсатора выбраны столь малыми, что конденсатор успевает зарядиться или разрядиться менее чем 1/100 с. Период собственных колебаний подвижной системы микроамперметра значительно больше этой величины. Устанавливая с помощью потенциометра известную разность потенциалов, измеряемую вольтметром, и измеряя показания микроамперметра, можно определить неизвестную емкость конденсатора . (2)Если все опыты проводились при одном и том же постоянном напряжении (например, 40 В) и если учесть, что частота  =50 Гц также постоянна, то расчетную формулу можно представить в таком окончательном виде . (3)При расчете погрешности  и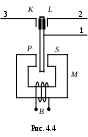сходим из формулы (2) . (4)П  огрешностью частоты переменного тока можно пренебречь ввиду ее малости. В качестве переключателя в работе применено специальное устройство – поляризованное реле. Схема его показана на рис. 4.4. На подковообразный железный сердечник M намотана намагничивающая катушка B, по которой поступает переменный ток с частотой 50 Гц. Посередине между концами сердечника M помещен намагниченный стержень-якорь. Если в катушке B тока нет, якорь располагается точно посередине между наконечниками P и S. Когда в катушке B идет ток, то создается магнитное поле, плоская пружина, удерживающая якорь в среднем положении, изгибается, и якорь притягивается к одному из полюсов P или S в зависимости от направления тока в катушке B. При этом клемма 1 соединяется через якорь и контакты K и L поочередно с клеммами 2 и 3. В результате (рис.4. 4) конденсатор  то заряжается, то разряжается 50 раз в секунду.Порядок выполнения работы и обработка результатов измерений Собрать схему согласно рис. 4.3, включая конденсатор неизвестной емкости  .Подключить схему к сети и с помощью потенциометра установить на конденсаторе напряжение U не более указанного на установке. Включить автоматический переключатель и измерить ток микроамперметром. Те же опыты проделать для второго конденсатора С2 и для их параллельного и последовательного соединений (все измерения провести по 3 раза и найти среднее значение измеряемых величин). По данным измерений определить емкости конденсаторов С1 и С2 и емкости при их последовательном и параллельном соединениях (  и  . Зная величины С1 и С2 теоретически рассчитать емкости батарей при последовательном и параллельном соединениях конденсаторов С/ и С// , (5) . (6)Сравнить их с измеренными и .Протокол наблюдений и результатов
Контрольные вопросы Что такое емкость конденсатора и от чего она зависит? Как рассчитать емкость конденсаторов, указанных на рис. 4.5? Случай а: пространство между пластинами заполнено диэлектриком с относительными проницаемостями  и  . Пластины из диэлектрика параллельны пластинам конденсатора. Случай б: то же самое, но пластины из диэлектрика расположены перпендикулярно пластинам конденсатора.И  зменится ли емкость сферического конденсатора, если одну из его пластин заземлить? Батарея из четырех одинаковых конденсаторов включена один раз по схеме а, а другой раз по схеме б, рис. 4.6. В каком случае емкость батареи будет больше? К 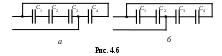 ак рассчитать приборную погрешность вольтметра, применяемого в данной работе?Литература 1. Гл.11. §93-94. С.167-176. 2. Гл.16. §16.1-16.3. С.219-228. 3. Гл. III. §26-27. С.82-84. 7. Гл.V. §5.1-5.5. С.109-114. Лабораторная работа 5 Экспериментальное изучение обобщенного закона Ома Приборы и принадлежности: вольтметр, миллиамперметр, постоянные сопротивления, реостат, два источника постоянного тока. Цель работы: экспериментальное изучение закона Ома для однородного и неоднородного участков цепи, т.е. исследование зависимости разности потенциалов от тока для двух разных схем. Измерение внутреннего сопротивления источника тока с заданной точностью, подбором для этого соответствующих электро-измерительных приборов с учетом их класса точности, , Rx. Элементы техники безопасности: при выполнении работы соблюдать правила техники безопасности с сетевым напряжением 220 В. Сборку схемы и соединение проводов производить только при выключенных источниках, а также проявить особое внимание при подключении и работе с измерительными приборами. Теоретическое введение Если в электрическом поле перемещаются электрические заряды, то силы поля совершают работу  , (1)отсюда  , т.е. разность потенциалов численно равна работе электрических сил по перемещению единичного положительного заряда из одной точки поля в другую.Элементарная работа электрических сил по перемещению заряда q0 из одной точки в другую  , отсюда  . (2)Из формул (1) и (2) следует, что  . (3)Под действием электрических сил положительные заряды перемещаются от точек поля с более высоким потенциалом к точкам с менее высоким. Электрические заряды перемещаются также под действием сил неэлектрического происхождения, они называются сторонними силами. Источниками таких сил являются, например, аккумулятор, динамо-машина. Под действием сторонних сил положительные заряды могут перемещаться от точек с менее высоким потенциалом к точкам с более высоким. Работа сторонних сил по перемещению заряда  . Отсюда  , (4)где  – напряженность поля сторонних сил.Из равенства (4) следует, что электродвижущая сила (ЭДС) численно равна удельной работе сторонних сил при перемещении заряда из точки 1 в точку 2. Работа перемещения заряда по замкнутому контуру совершается только сторонними силами, а на отдельных участках цепи как сторонними, так и электростатическими силами. Величина, численно равная сумме удельных работ электрических и сторонних сил, называется электрическим напряжением, которое равно:  . (5)По закону Ома напряжение на участке цепи равно произведению силы тока на полное сопротивление участка. Следовательно, для участка цепи, содержащего сторонний источник, закон Ома в обобщенном виде может быть записан 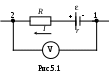 , (6)где  – полное сопротивление участка, которое складывается из внешнего (включенная нагрузка, провода и т.д.) и внутреннего сопротивления источника. Применяя обобщенный закон Ома, необходимо помнить о направлении обхода участка цепи: произведение  следует брать со знаком плюс, если направление тока совпадает с направлением обхода; ЭДС следует брать со знаком плюс, если ее направление (от минуса к плюсу) внутри источника совпадает с направлением обхода. Следует помнить, что вольтметр измеряет разность потенциалов между точками подключения прибора.Рассмотрим участок цепи, изображенный на рис. 5.1 Выберем направление для участка цепи 1-2 от точки 1 к точке 2. Тогда  . (7)Здесь r – внутреннее сопротивление источника; ri – сопротивле-ние проводов. Не зная параметров внешней (по отношению к рассматриваемому участку) цепи невозможно заранее указать отклонение стрелки вольтметра, т.е. нельзя сказать потенциал какой точки (1 или 2) будет выше. Показание вольтметра в общем случае будет:  . (8)Так как V мы всегда подключаем так, чтобы он отклонялся в правую сторону шкалы прибора, то V может быть и с знаком «-». Заменяя в выражении (7) разность потенциалов через показания вольтметра, получим:  ,или  . (9)Таким образом, между разностью потенциалов, измеряемой вольтметром на концах любого участка цепи, и током, текущим в любом участке, в общем случае существует линейная зависимость, а не просто прямая пропорциональность. Из формулы (9) видно, что в пределе при токе, стремящемся к нулю, вольтметр будет показывать ЭДС источника, включенного в рассматриваемый участок. |