Газодинамические функции 2008. Газодинамические функции
 Скачать 141.5 Kb. Скачать 141.5 Kb.
|
|
ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ Газодинамические функции параметров торможения τ(λ), π(λ), ε(λ). Зависимости между истинными параметрами состояния газа и параметрами торможения (далее по тексту отмечены «звездочкой») приобретают особенно удобный для расчетов вид, если их представить с помощью безразмерных скоростей М и λ . Для того чтобы получить эти зависимости, определим сначала отношения температур Т*/Т и обратную величину Т/Т*  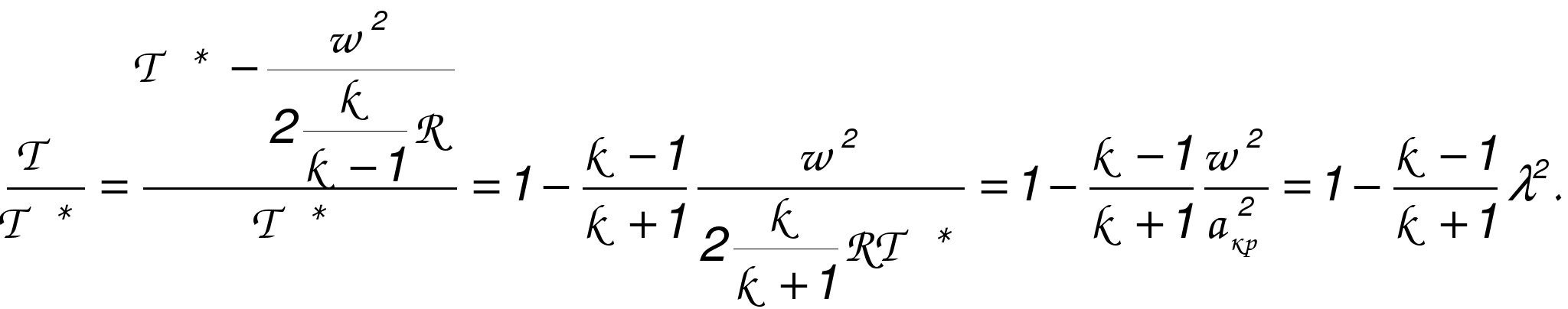 Отношения давлений и плотностей можно выразить с помощью уравнений изоэнтропного процесса (2.33)1 через температуры. Тогда 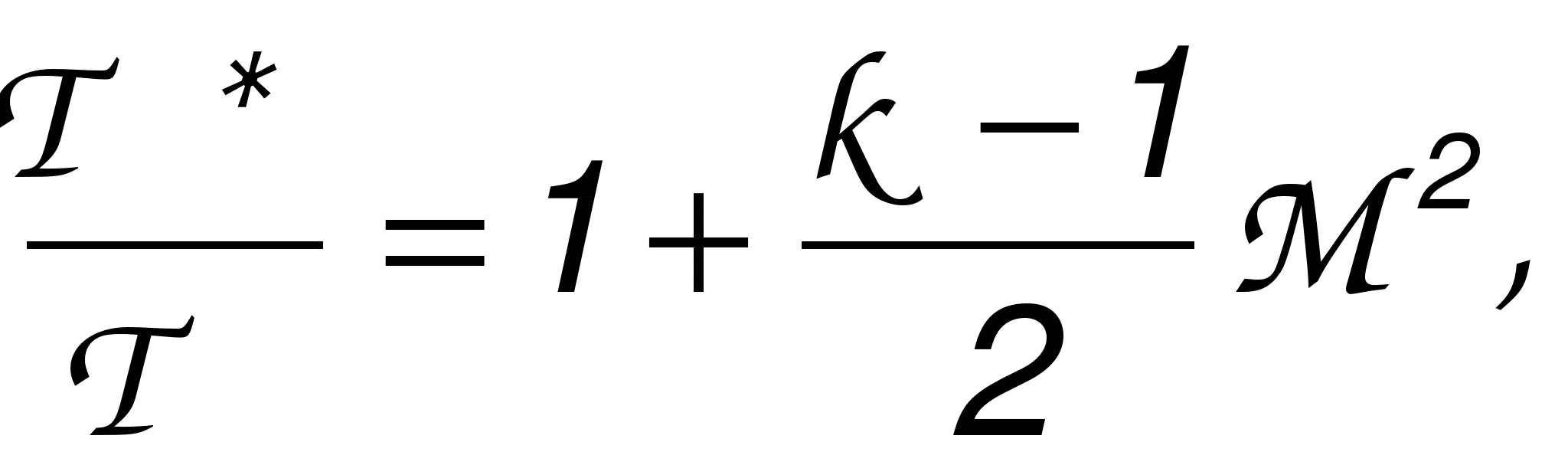 (2.56) (2.56)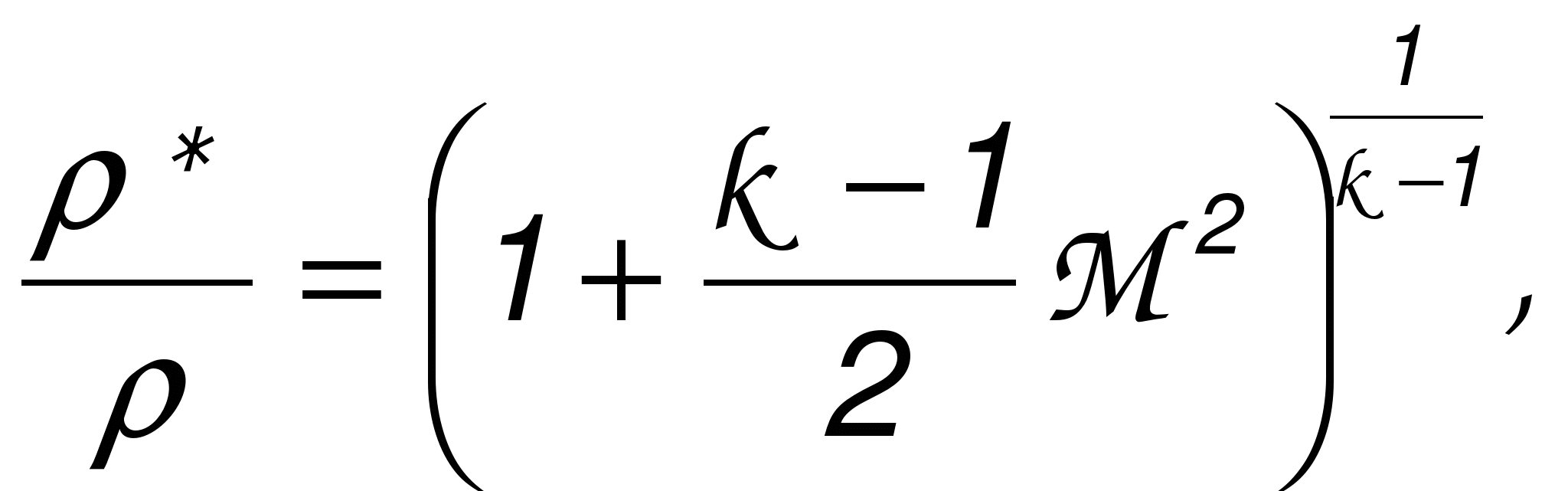 (2.57) (2.57)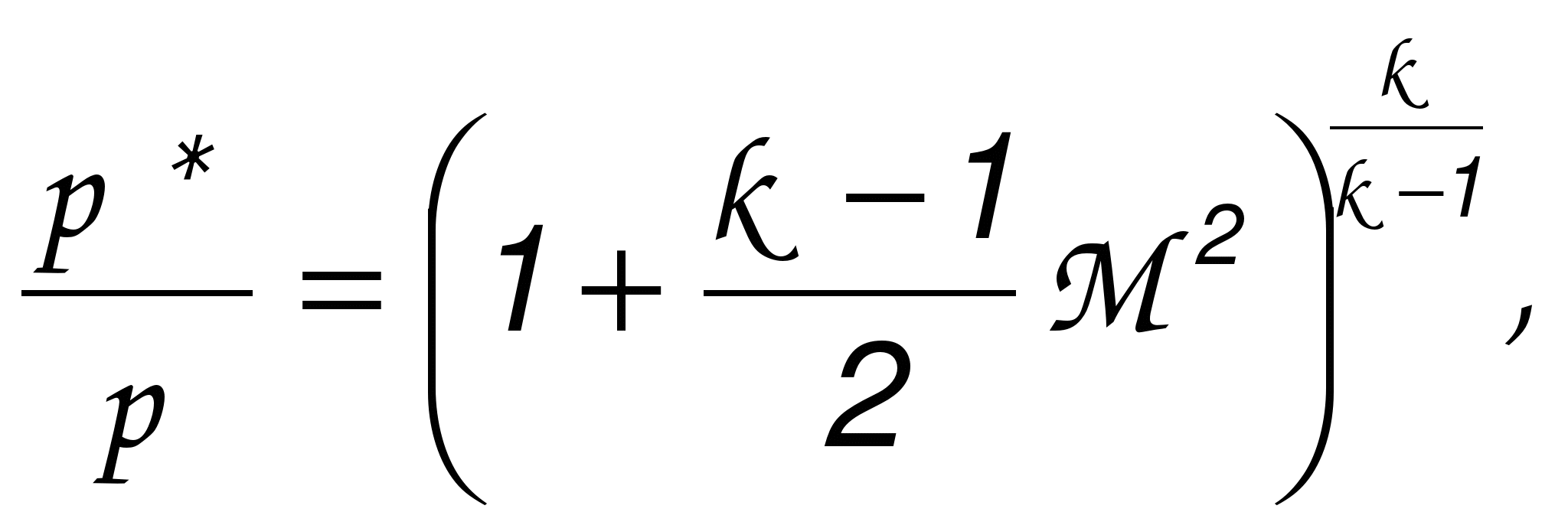 (2.58) (2.58)и 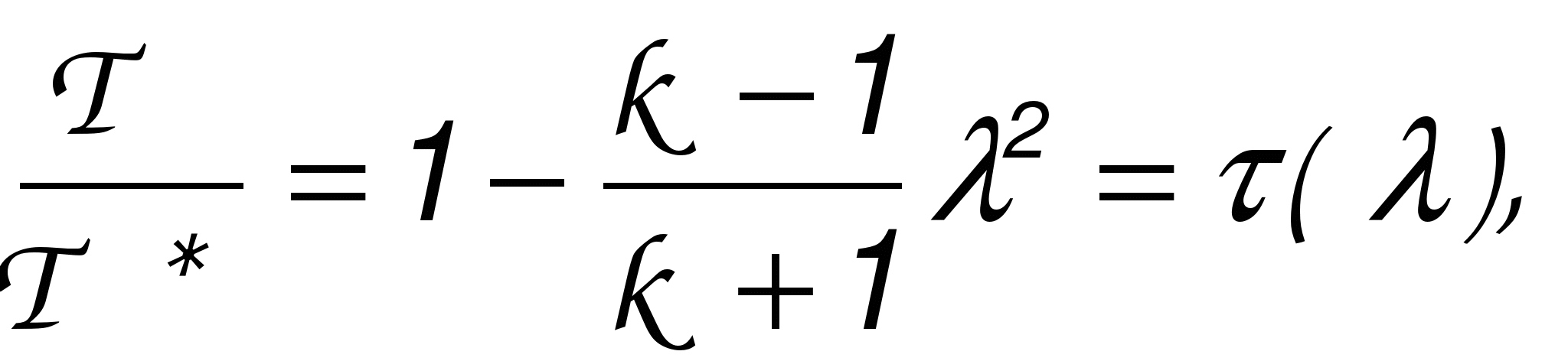 (2.59) (2.59) (2.60) (2.60)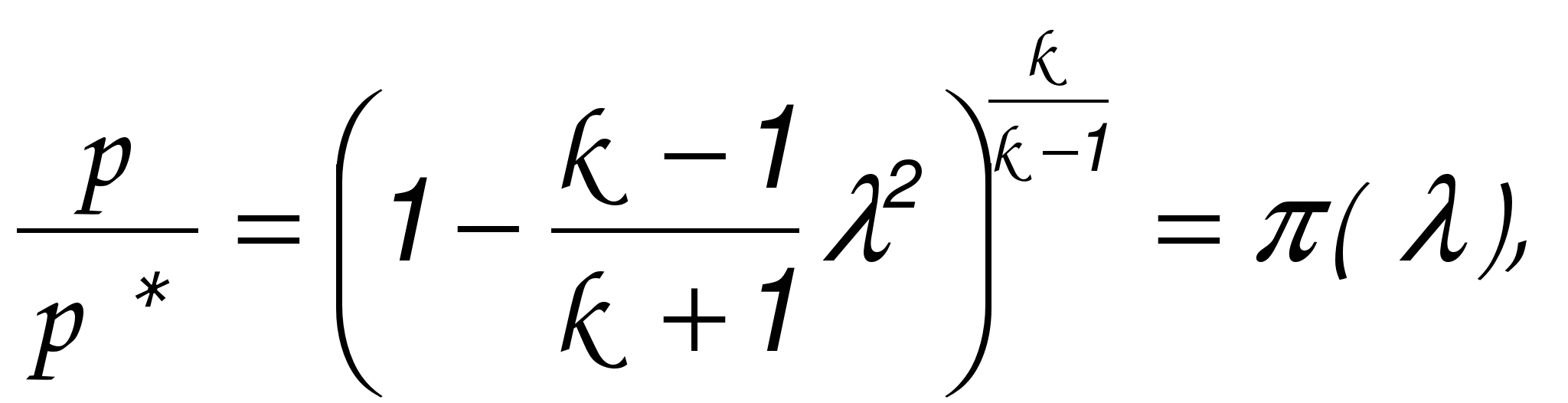 (2.61) (2.61)Величины τ(λ), π(λ), и ε(λ) называются газодинамическими функциями параметров торможения. Они заранее рассчитываются для всех значений приведенной скорости λ (или М) и сводятся в таблицы газодинамических функций. Последние составляются для различных значений показателя изоэнтропы k, соответствующих разным газам. Для воздуха (при k = 1,4) формулы, связывающие истинные параметры состояния с параметрами торможения, принимают следующий вид: 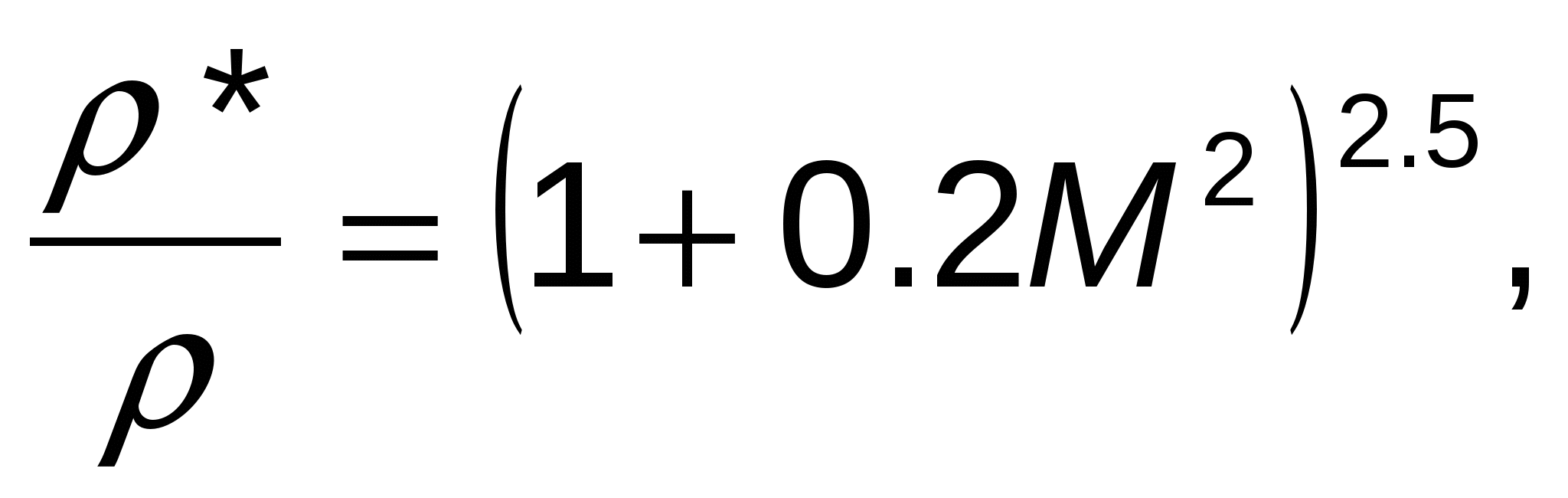 (2.63) (2.63)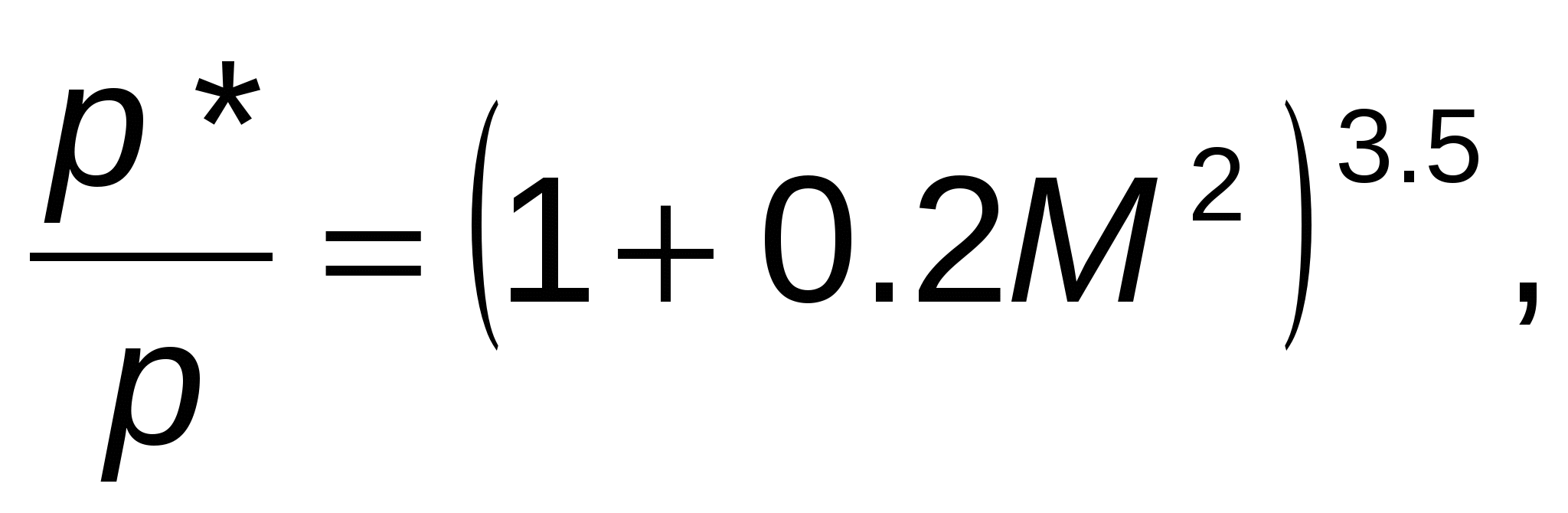 (2.64) (2.64)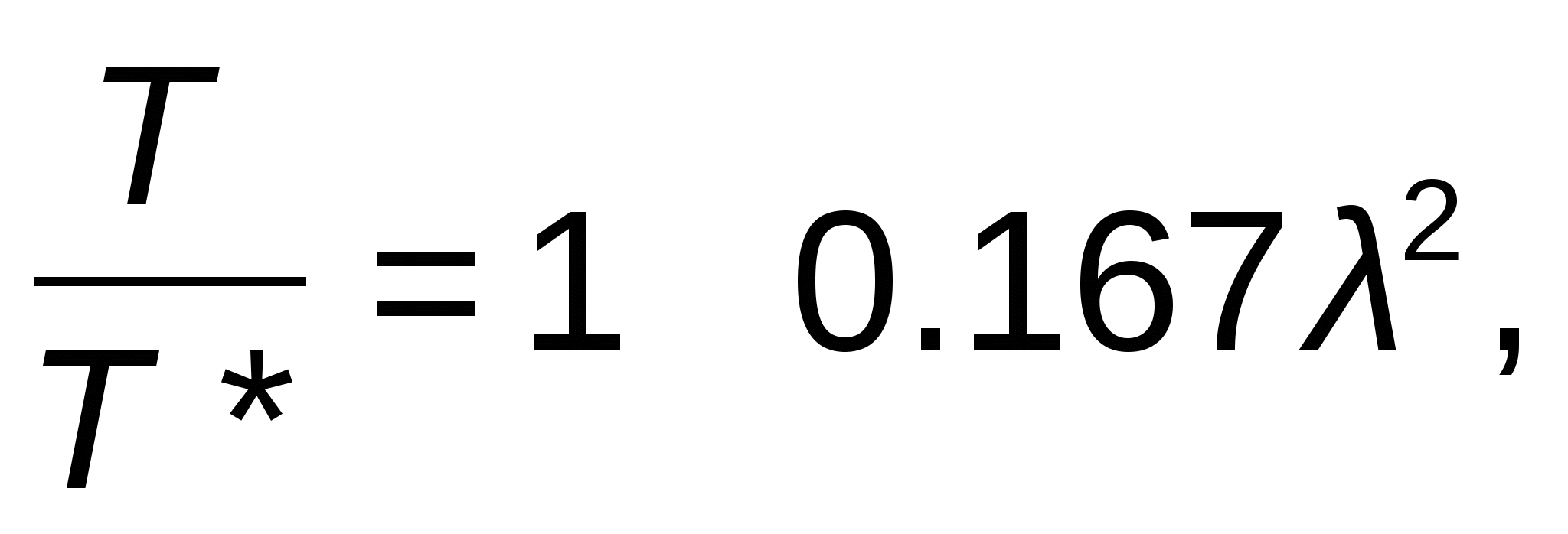 (2.65) (2.65)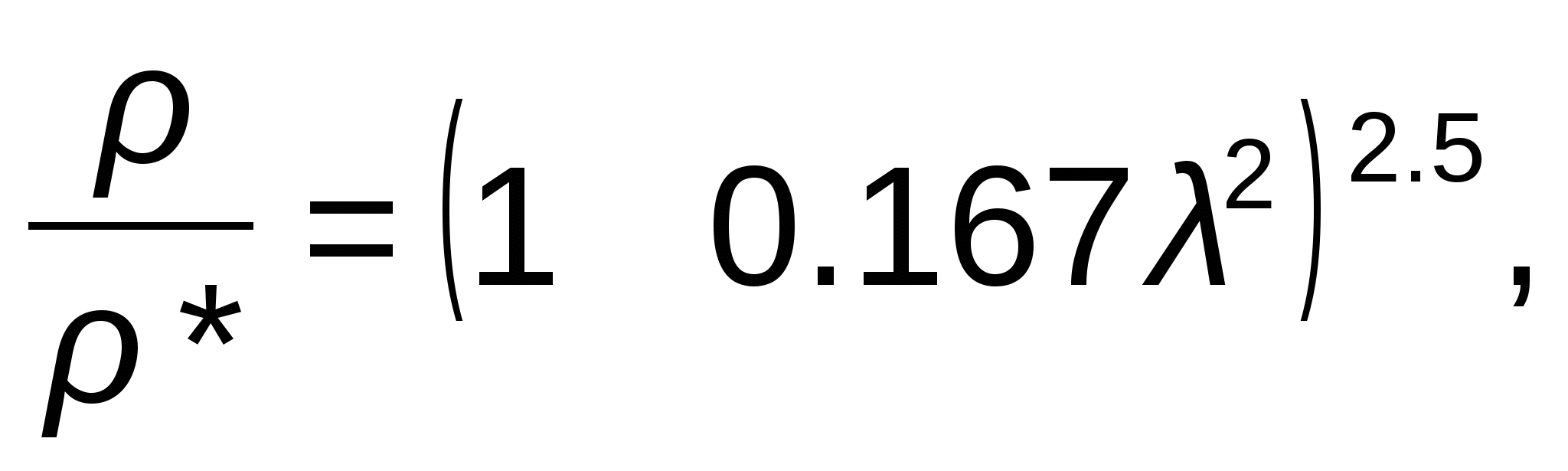 (2.66) (2.66)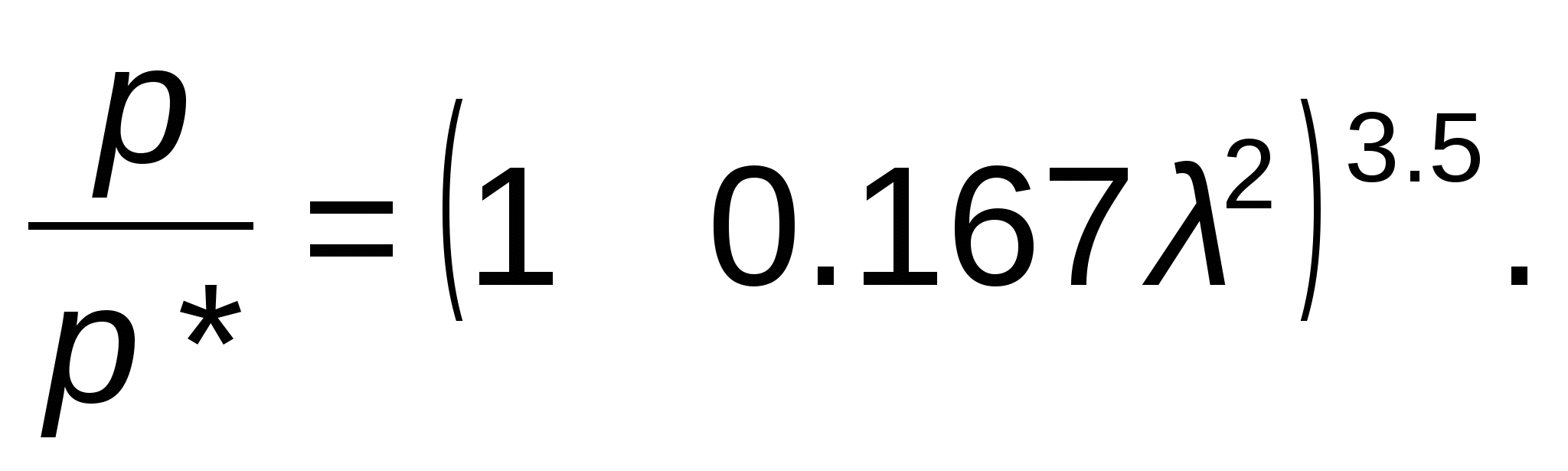 (2.67) (2.67)Пример расчета с помощью газодинамических функций параметров торможенияВ потоке воздуха были измерены: давление и температура торможения - р*= 143000н/м2, Т* = 324 оК, статическое давление - р = 101300 н/м2 (нормальное атмосферное или барометрическое давление В = 760 мм рт ст). Определить w(скорость потока). 1) Вычисляем 2) Определяем критическую скорость 3) По таблицам газодинамических функций для воздуха (k=1,4) по величине π(λ) =0,7085 находим λ=0,75. 4) Определяем скорость w = λaкр = 0,75∙329,6 = 247,2 м/сек. Как видно из приведенного примера, весь расчет сводится к очень простым операциям. Таблицы газодинамических функций были особенно эффективны при массовых расчетах в “докомпьютерную” эпоху. *** Газодинамические функции потока массы (расхода) q(λ), y(λ) В практических расчетах площадь поперечного сечения потока F и плотность тока рw удобно относить к соответствующим величинам, взятым в критическом сечении. Если, например, рассматривать сопло Лаваля, то уравнение неразрывности можно записать, приравняв расход в любом сечении расходу в критическом сечении ρwF = ρкр акр Fкр, в следующем виде: Левая часть этого равенства — безразмерная плотность тока — называется приведенным расходом или коэффициентом расхода. Она обозначается q(λ), т.е. Плотность тока рw характеризует расход газа через единицу поверхности или площади поперечного сечения. Приведенный расходпредставляет собой расход через единицу площади, отнесенный к расходу через единицу площади в критическом сечении. Эта величина является функцией только приведенной скорости λ и показателя изоэнтропы k. Действительно, принимая во внимание формулы (2.61) и (2.45)2, можно написать 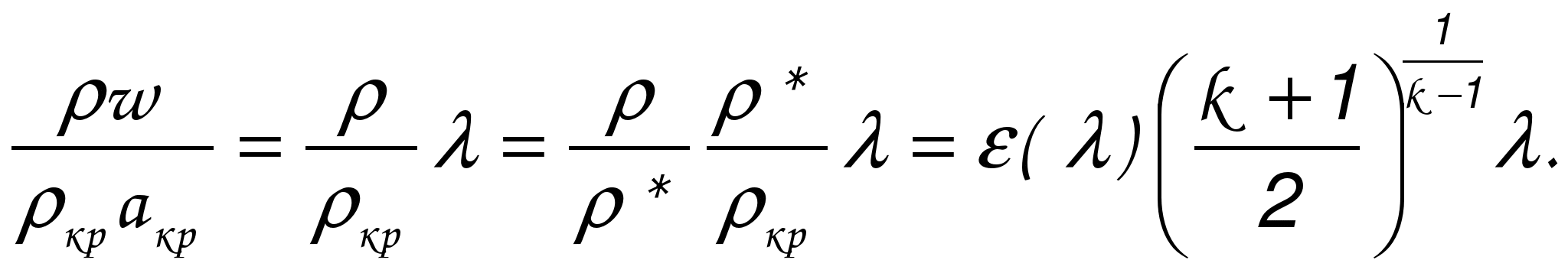 или По формуле (2.80) легко определяются три характерные точки: λ=0 q(λ)=0, λ=1 q(λ)=1, λ= Промежуточные значения получаются численным расчетом. График зависимости приведенного расхода от приведенной скорости представлен на рис. 23. Наибольшая величина q(λ)=1 получается, как видим, при λ=1. Следовательно, наибольшую плотность тока газ имеет в критическом сечении. При λ<1 расход уменьшается за счет уменьшения скорости, а при λ>1 — за счет уменьшения плотности газа. Рассматривая график на рис. 23 и формулу (2.78), легко уяснить, почему сопло Лаваля имеет такую форму. Постоянство расхода требует того, чтобы площадь канала уменьшалась в тех местах, где возрастает плотность тока, и увеличивалась там, где плотность тока падает. В том сечении, где плотность тока проходит через максимум, канал должен иметь горло. Заметим, кстати, что одной из причин невозможности достижения максимальной скорости потока является то обстоятельство, что при w=wmax, т.е. при λ= С помощью функции q(λ) удобно вычислять массовый расход в любом сечении потока. Он записывается так: 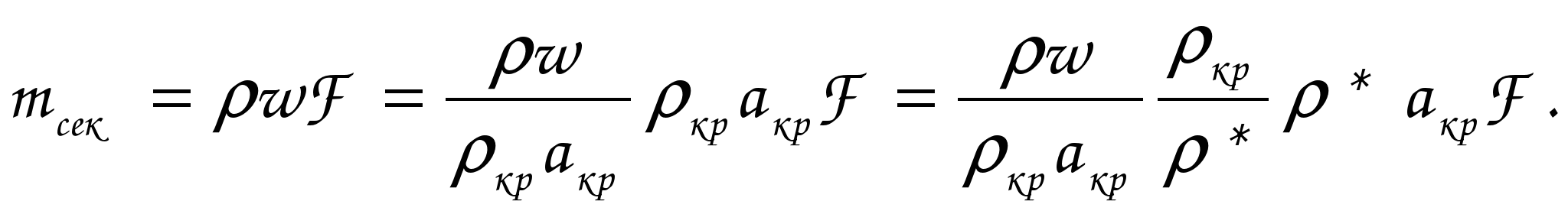 Принимая во внимание формулы (2.79), (2.45), (2.46), а также уравнение состояния совершенного газа (p=RT), можно предыдущее выражение представить в следующем виде: 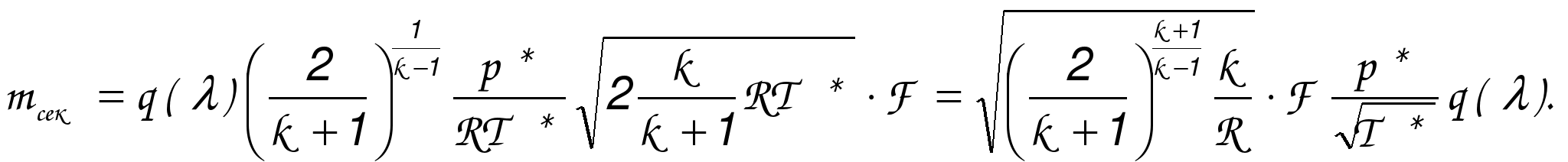 Величина для данного газа постоянна. Для воздуха она равна ( k = 1,4; R = 287,4 дж/кг град) — m = 0,04037. Окончательно формула расхода приобретает вид 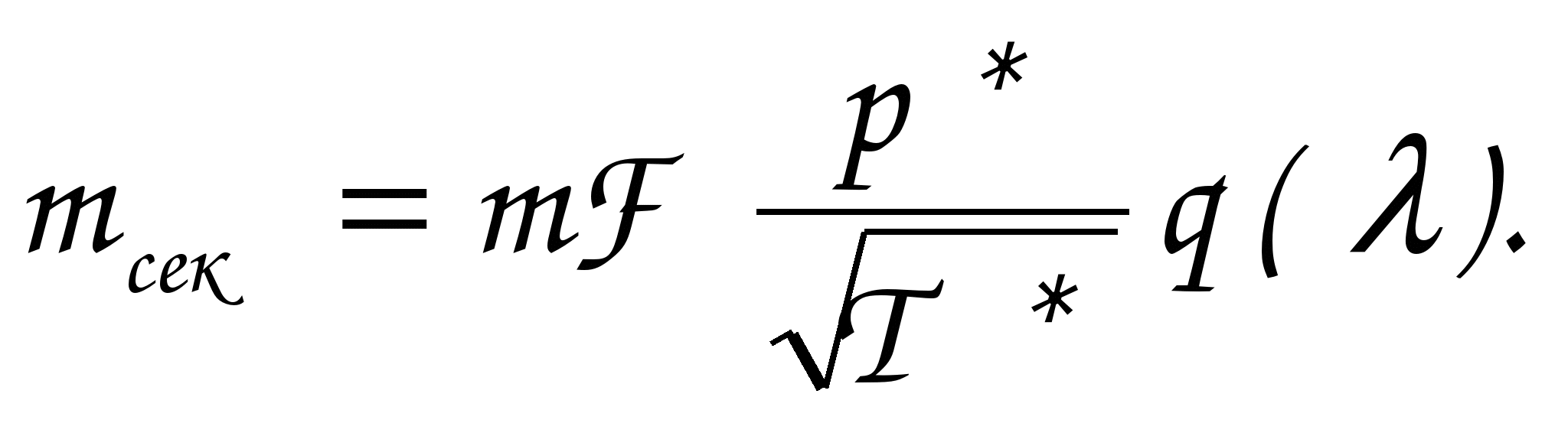 (2.81) (2.81)Часто известной величиной бывает не р*, а статическое давление р. Так как то 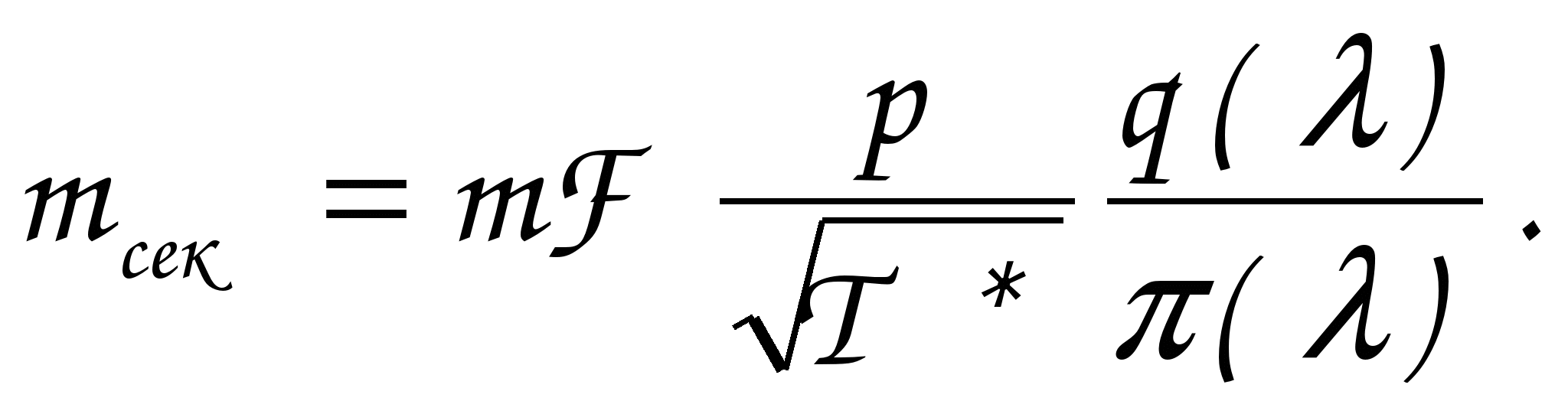 Отношение 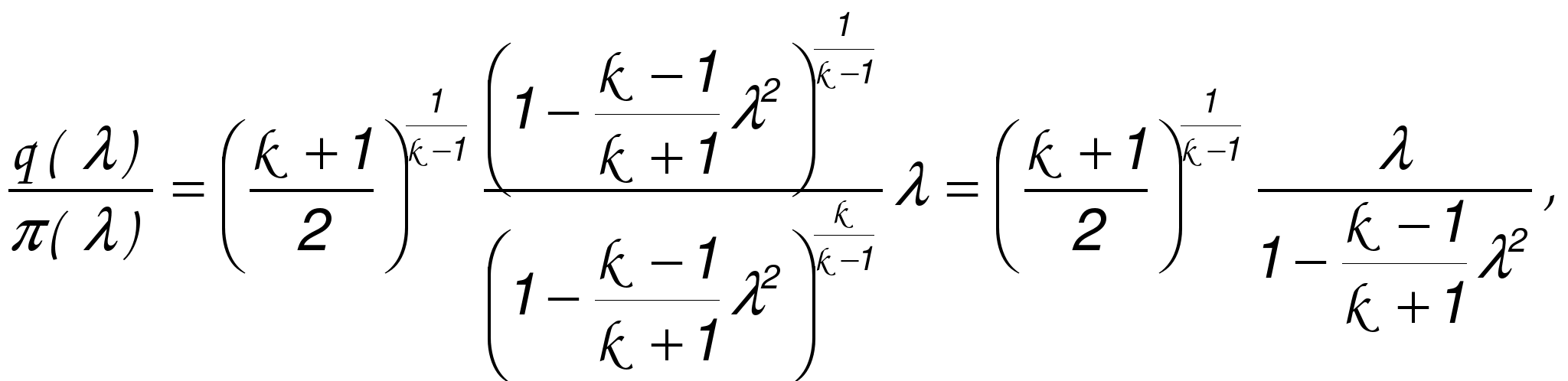 т.е. 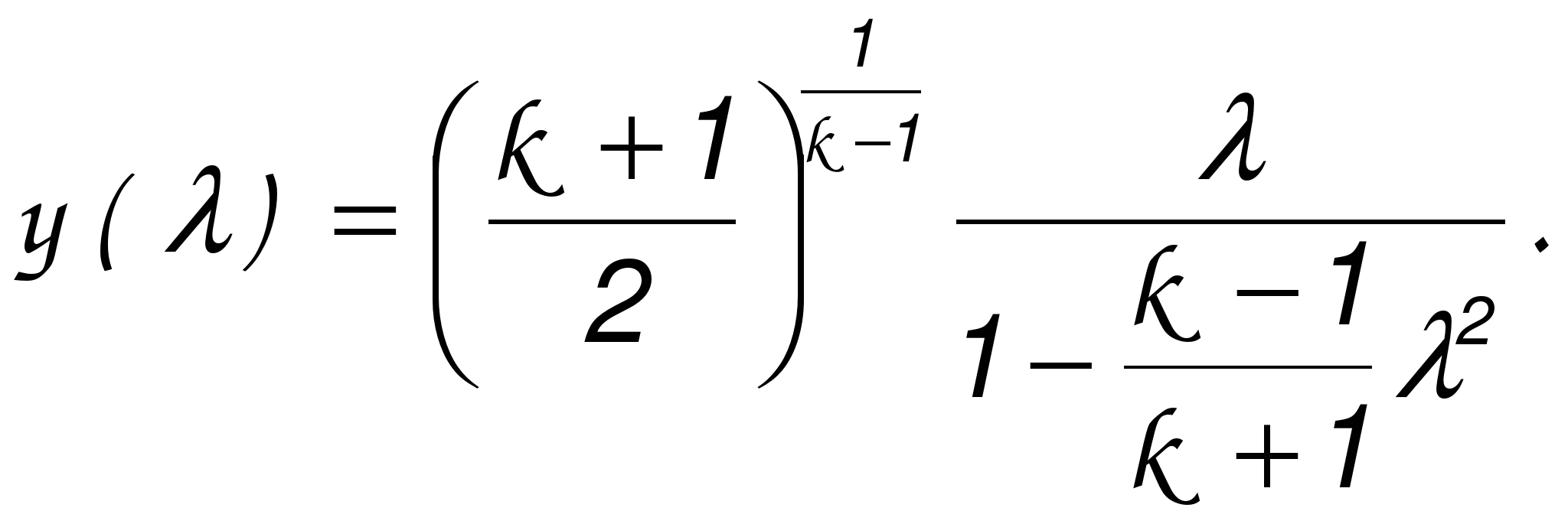 (2.82) (2.82)Тогда 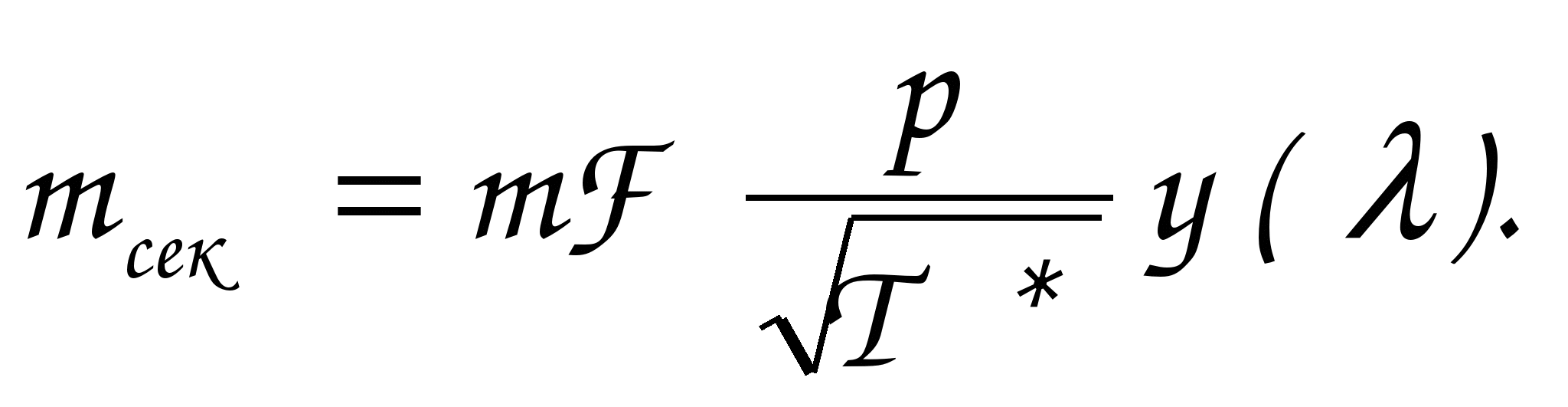 (2.83) (2.83)При вычислении расхода газа через сопло Лаваля или другой канал, в котором имеется критическое сечение, расчет ведется по параметрам в этом сечении. Так как в этом месте q(λ)=1, то расчетная формула имеет вид 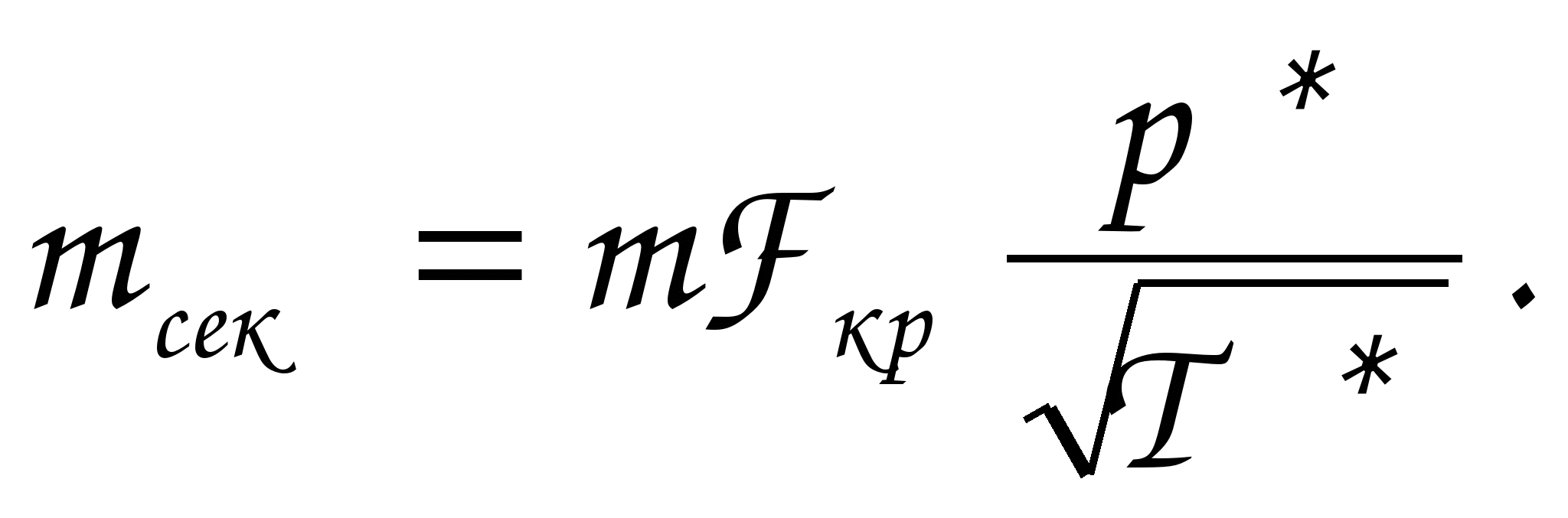 (2.84) (2.84)Пример определения проходных сечений сопла Лаваля с помощью таблиц газодинамических функций. 3адано: расход газа mсек = 10 кг/сек; физичеcкие константы воздуха k=1,4; R=287,4 дж/кг град, параметры перед соплом и за ним: p 1* =37,24 p 2* =1,013 T 1* =324°K. Определить: скорость истечения w2, площадь поперечного сечения в горле FГ, площадь поперечного сечения на выходе F2. Рассчитывается идеальный случай — энергоизолированное изоэнтропное течение, в котором соблюдаются условия постоянства давления и температуры заторможенного потока: Т1*= ТГ* = Т2* = Т*= const, р1*= рГ* = р2* = р*= const. 1. 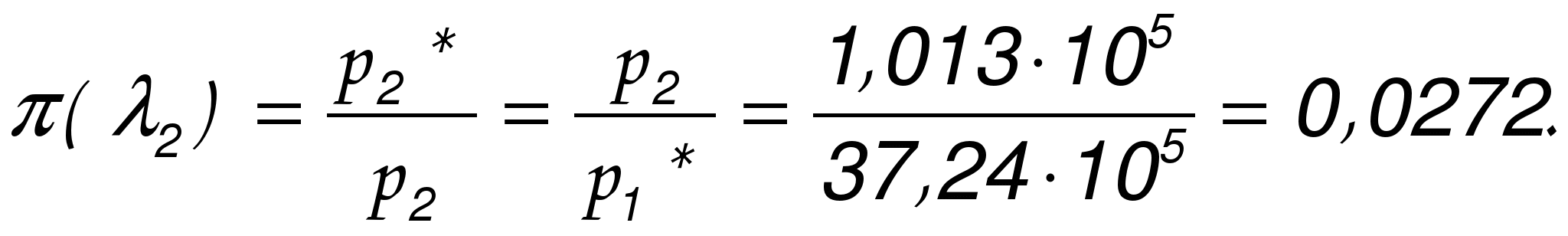 2. По таблицам газодинамических функций для k=1,4 находим при 3. 
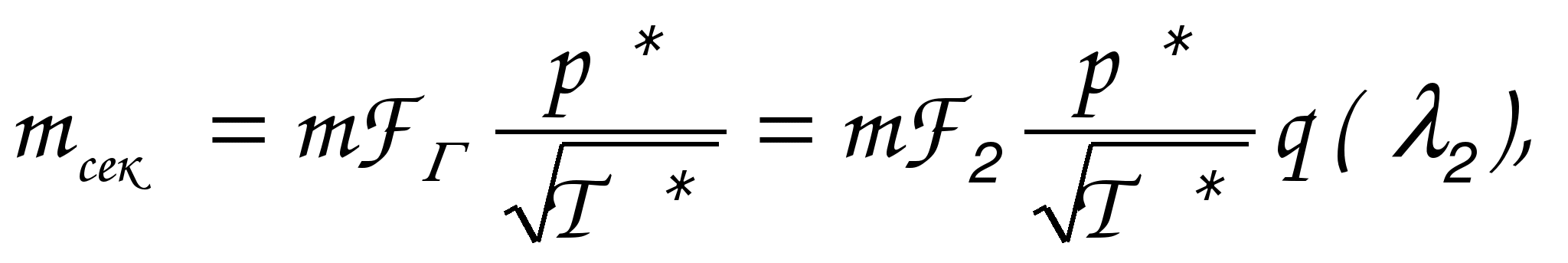 то По таблицам газодинамических функций при λ2=1,964 находим q(λ2)=0,2362. Тогда F2 = 0,0012 / 0,2363 = 0,00507 м2 = 50,7 см2. Размеры всех промежуточных сечений получаются при профилировании сопла. 1 См. файл Параметры торможения.pdf 2 См. файл Параметры торможения.pdf из |
