Отчет_Св. Генерация входной последовательности

Название	Генерация входной последовательности
Дата	28.11.2018
Размер	0.92 Mb.
Формат файла
Имя файла	Отчет_Св.doc
Тип	Документы #58070

Задание

Генерация входной последовательности.

Сигнал составленный из подпоследовательностей различной частоты (3, 7, 10, 25Гц)

Равное число периодов задания подпоследовательностей сигнала Рабочий диапазон частот: 0.5-25 Гц;

Частота дискретизации: 128 Гц;

Длина реализации: 512 отсчетов;

Амплитуда сигнала в диапазоне от -500 мкВ до 500 мкВ.

Реальный сигнал

Последовательность 16-разрядных чисел со знаком;

Частота дискретизации 256 Гц;

Амплитуда сигнала +/-50мкВ соответствует +/-400 единицам кода;

Файл с реальным сигналом: Signal.d04.

Реализация спектрального анализа с использованием БПФ

Вычислить прямое и обратное дискретное преобразование Фурье для взвешенной с помощью окна реализации сигнала с использованием функций одномерного преобразования FFT и IFFT, построить график модуля спектральной функции.

Использовать окна, задаваемые функциями CHEBWIN(n, r) и HANNING(n).

Проектирование и реализация цифрового фильтра

Выполнить расчет заданного ЦФ, построить АФЧХ. Фильтрация входного сигнала, построение графика выходного сигнала и модуля спектральной функции.

БИХ фильтр:

фильтр Чебышева 1 рода;

полоса пропускания: 0 – 25 Гц;

затухание в полосе пропускания -3дБ;

затухание вне полосы пропускания не хуже -20дБ.

Теоретическая часть

1. Спектральный анализ
Прямое и обратное ДПФ

Для выполнения прямого и обратного ДПФ в MATLAB служат функции fft и ifft:

у = fft(x) — вычисляет прямое ДПФ для вектора х; если х — матрица, преобразование производится для каждого ее столбца по отдельности;
у = fft(x, N) — предварительно приводит исходные данные к размеру N, урезая их или дополняя нулями;
х = ifft(y) и х = ifft(y, N) — аналогичные варианты вызова для функции обратного ДПФ.

Функции fft и ifft входят в базовую библиотеку MATLAB. Вычисления организованы так, что реализуется максимально возможное для каждой длины исходного вектора ускорение вычислений: длина вектора (число строк в матрице) х раскладывается на простые множители, число этих множителей соответствует количеству ступеней БПФ, а сами множители определяют коэффициенты прореживания на разных ступенях БПФ.
Окна

MATLAB содержит (в пакете Signal Processing) целый ряд стандартных весовых функций. Они возвращают векторы отсчетов, которые могут использоваться в качестве одного из параметров разнообразных функций непараметрического спектрального анализа.

Все рассматриваемые ниже функции принимают в качестве параметра требуемую длину вектора (n), которая должна быть целым положительным числом, и возвращают вектор-столбец w. При n=1 все функции возвращают значение 1.

Амплитудный спектр весовой функции соответствует частотной характеристике нулевого канала ДПФ при использовании данной весовой функции. При рассмотрении конкретных функций графики их амплитудных спектров будут строится в логарифмическом масштабе для n=16. Чтобы обеспечить на нулевой частоте значение спектральной функции, равное единице (0 дБ), перед вычислением спектра весовые функции нормируются – делятся на сумму своих отсчетов.

Графики функций будут строиться функцией freqz.

FREQZ – частотная характеристика цифрового фильтра.

Когда N целое, [H,W] = FREQZ(B,A,N) возвращает для вектора частот W в радианах N-точечную комплексную частотную характеристику в векторе H фильтра B/A: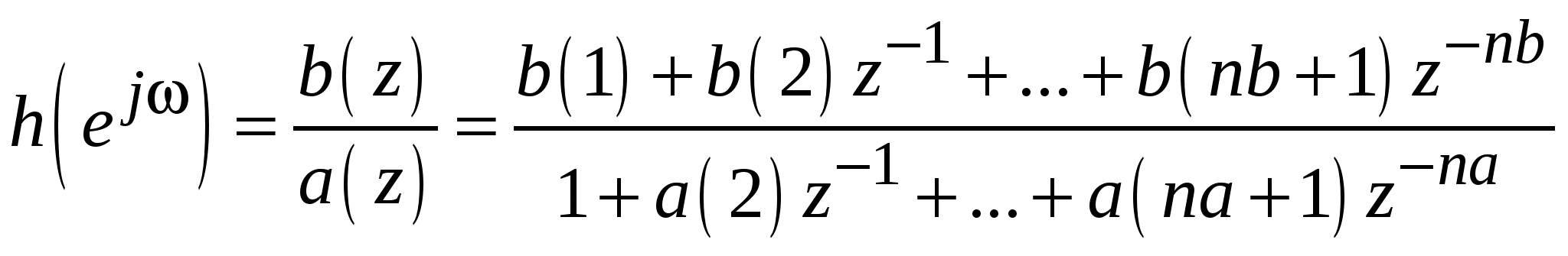

.

Частота отклика оценивается в N точках одинаково расположенных интервалов верхней половины единичной окружности. Если N не определено, то по умолчанию равно 512.

[H,W] = FREQZ(B,A,N,'whole') использует N точек по всей окружности.

H = FREQZ(B,A,W) возвращает частоту отклика на частотах, назначенных в векторе W, в радианах (нормально между 0 и ).

[H,F] = FREQZ(B,A,N,Fs) и [H,F] = FREQZ(B,A,N,'whole',Fs) на заданной частоте дискретизации Fs (в герцах) возвращают вектор частот F (в герцах).

H = FREQZ(B,A,F,Fs) на заданной частоте дискретизации Fs (в герцах) возвращает комплексную частоту ответа на частотах, определенных в векторе F(в герцах).

FREQZ(B,A,...) без выходных аргументов рисует амплитуду и развернутую частоту B/A в текущем графическом окне.

Окно Чебышева

Функция CHEBWIN реализует окно Чебышева:

w = chebwin(n, r).

Отсчеты окна Чебышева рассчитываются по следующей формуле: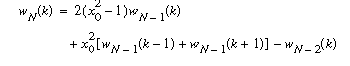

Окно Ханнинга

Функция HANNING реализует окно Ханнинга:

w = hanning(n)

Окно Ханнинга может быть применено в частотной области с использованием реккурентной формулы:

Обобщённое окно Ханнинга:

a

= 0,54, окно Хэмминга

a = 0,5, окно Ханнинга

Общая характеристика цифровых фильтров

Различают два общих класса сигналов: аналоговые и дискретные. Аналоговым сигналом называется сигнал, определенный для каждого момента времени, дискретным сигналом – сигнал, определенный только в дискретные моменты времени. Как дискретный, так и аналоговый сигналы могут быть однозначно представлены некоторыми функциями частоты, которые называются их частотными спектрами.

Фильтрацией называется процесс изменения частотного спектра сигнала в некотором желаемом направлении. Этот процесс может привести к усилению или ослаблению частотных составляющих в некотором диапазоне частот, к подавлению или выделению какой-нибудь конкретной составляющей и т. п.

Цифровым фильтром называется цифровая система, которую можно использовать для фильтрации дискретных сигналов. Он может быть реализован программным методом или с помощью специальной аппаратуры, и в каждом из этих случаев цифровой фильтр можно применить для фильтрации сигналов как в реальном времени, так и предварительно записанных.

Цифровой фильтр можно представить структурной схемой, изображенной на рис. 1.1. На этой схеме x(n) и y(n) – соответственно, входное воздействие и реакция фильтра на это воздействие. Функционально они связаны соотношением

,

где вид оператора

зависит от свойств конкретной системы.

Рис. 1.1

Реакцию цифрового фильтра на произвольное воздействие можно представить с помощью импульсной характеристики фильтра. Допустим, что x(n) – входная, а y(n) – выходная последовательности фильтра и пусть h(n) – отклик на единичный импульс, называемый импульсной характеристикой. Тогда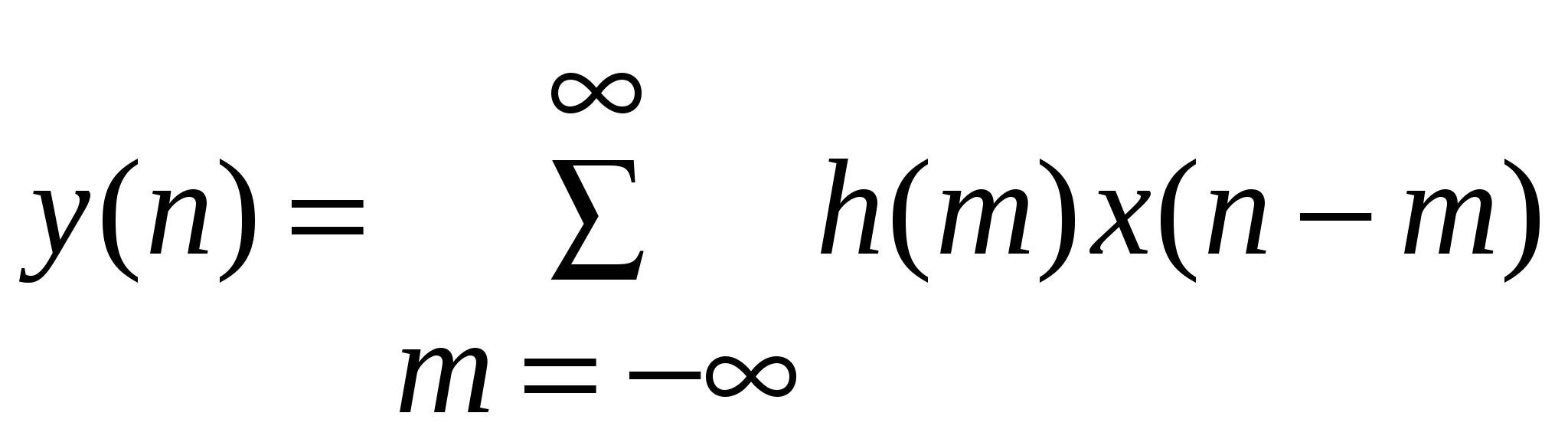

.

Таким образом, x(n) и y(n) связаны соотношением типа свертки. Частотная характеристика фильтра определяется следующим выражением: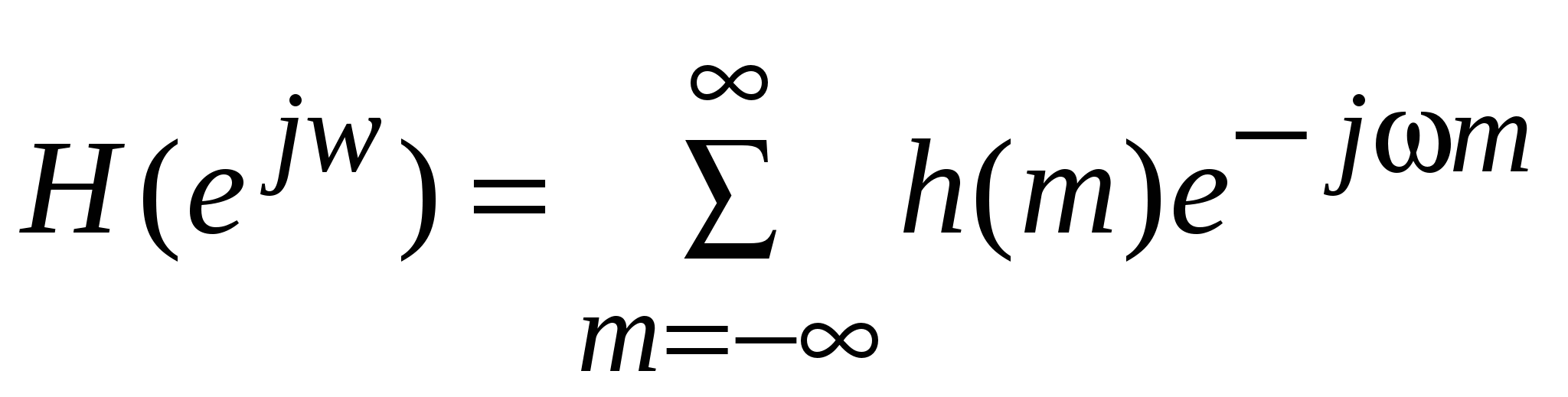

. (1.1)

Поскольку частотная характеристика является периодической функцией частоты , равенство (1.1) можно рассматривать как разложение

в ряд Фурье, причем коэффициенты являются одновременно отсчетами импульсной характеристики. Согласно теории рядов Фурье, коэффициенты h(n) могут быть выражены через

.

Из этого соотношения видно, что h(n) по существу является суперпозицией синусоид

с амплитудами

, которые можно представить следующим образом:

.

Выражение

называют амплитудной характеристикой фильтра, а

– фазовой характеристикой фильтра.

Свойства цифровых фильтров

Цифровой фильтр называется стационарным, если его параметры не изменяются во времени, т. е. предварительно невозбужденный фильтр, в котором x(n) = y(n) = 0 при всех n< 0, называют стационарным тогда и только тогда, когда для всех возможных воздействий.
Цифровой фильтр называют линейным тогда и только тогда, когда для всех a и b – произвольных постоянных и для всех допустимых воздействий x₁(n) и x₂(n).
Цифровой фильтр называют физически реализуемым, если величина отклика при n= n₀ зависит только от значений входной последовательности с номерами n£ n₀. Это означает, что импульсная характеристика h(n) равна нулю при n< 0.
Цифровой фильтр называется устойчивым тогда и только тогда, когда реакция на ограниченное воздействие ограничена, т. е. если из при всех n следует при всех n. Необходимым и достаточным условием устойчивости фильтра является следующее требование к его импульсной характеристике:

Представление цифрового фильтра в виде разностного уравнения

Цифровой фильтр в общем виде представляется следующим образом как разностное уравнение:

, (1.2)

где a_j и b_i – вещественные или комплексные коэффициенты.

Цифровые фильтры принято делить на два класса: нерекурсивные (НФ) и рекурсивные (РФ). Если в (1.2) все коэффициенты a_j = 0, что соответствует отсутствию обратной связи, то фильтр является нерекурсивным и описывается уравнением

. (1.3)

Если в (1.3) хотя бы один из коэффициентов a_j  0, то фильтр является рекурсивным и представляет собой устройство с обратной связью.

Таким образом, для рекурсивных фильтров соотношение между входной последовательностью {x(n)} и откликом фильтра {y(n)} может быть записано следующим образом:

, (1.4)

т. е. текущий отсчет отклика y(n) определяется не только текущим и предшествующим значениями входной последовательности, но и предшествующими отсчетами отклика.

В нерекурсивных фильтрах связь между входной последовательностью и откликом имеет вид

,

т. е. текущий отсчет отклика зависит от текущего и предшествующих значений входной последовательности.

Для анализа систем, описываемых разностными уравнениями, широко применяется z-преобразование. Прямое z-преобразование X(z) последовательности x(n)определяется формулой

. (1.5)

В разностных уравнениях существенной операцией является единичная задержка, описываемая оператором 1/z, или z^–1 (т. е. для последовательности x(n–1) z-преобразование будет иметь вид z^–¹X(z).

Передаточной (системной) функцией H(z) цифрового фильтра называется отношение z-преобразований выходного Y(z)и входного X(z)сигналов фильтра. Для рекурсивного и нерекурсивного фильтров из (1.3) и (1.4), используя (1.5), получаем:

Комплексная частотная характеристика цифрового фильтра, представленного в виде разностного уравнения (1.2), может быть получена подстановкой в выражение для передаточной функции значения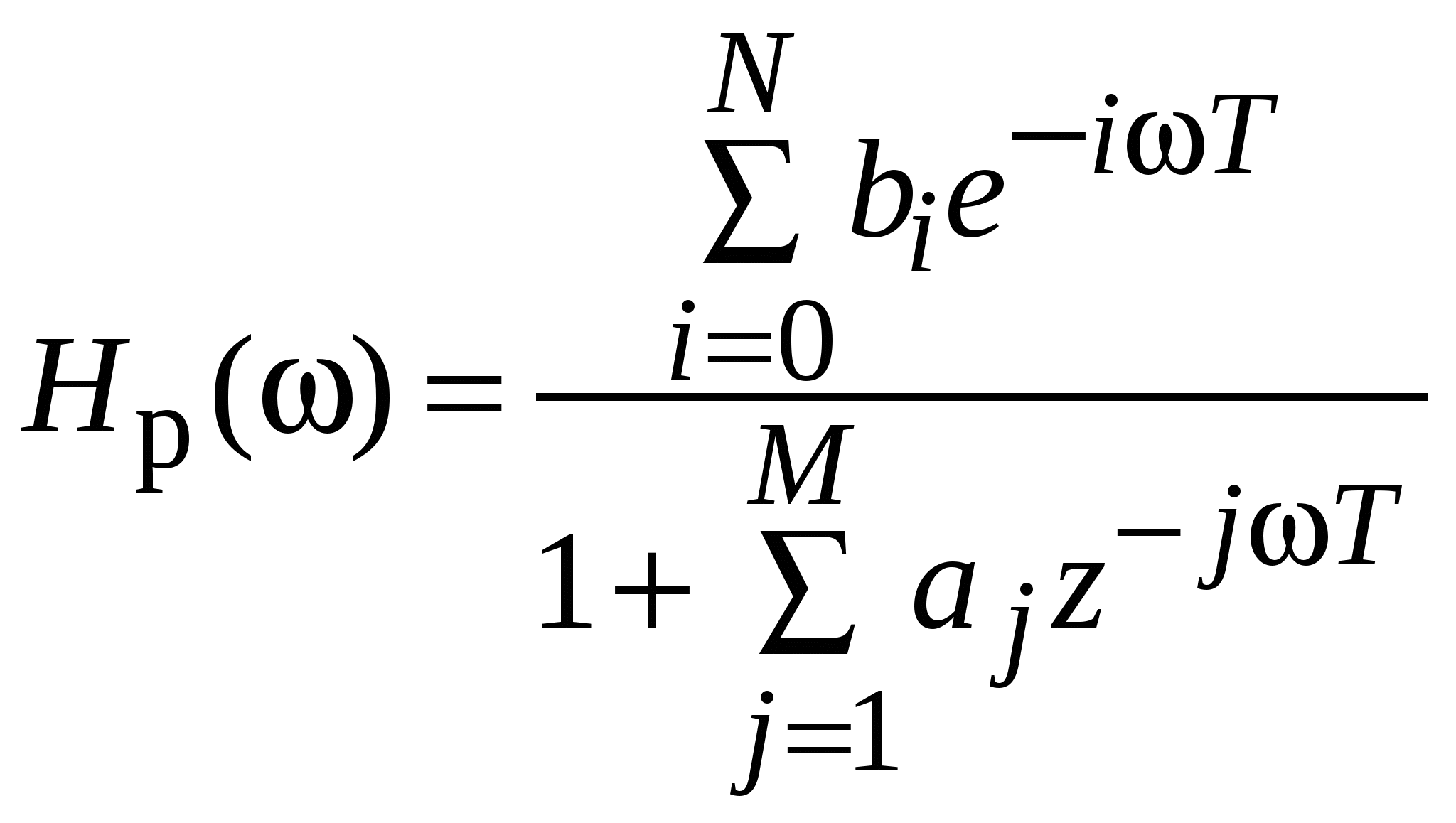

. Для рекурсивного фильтра общего вида частотная характеристика будет иметь вид

.

Аналогично, для нерекурсивного фильтра имеем: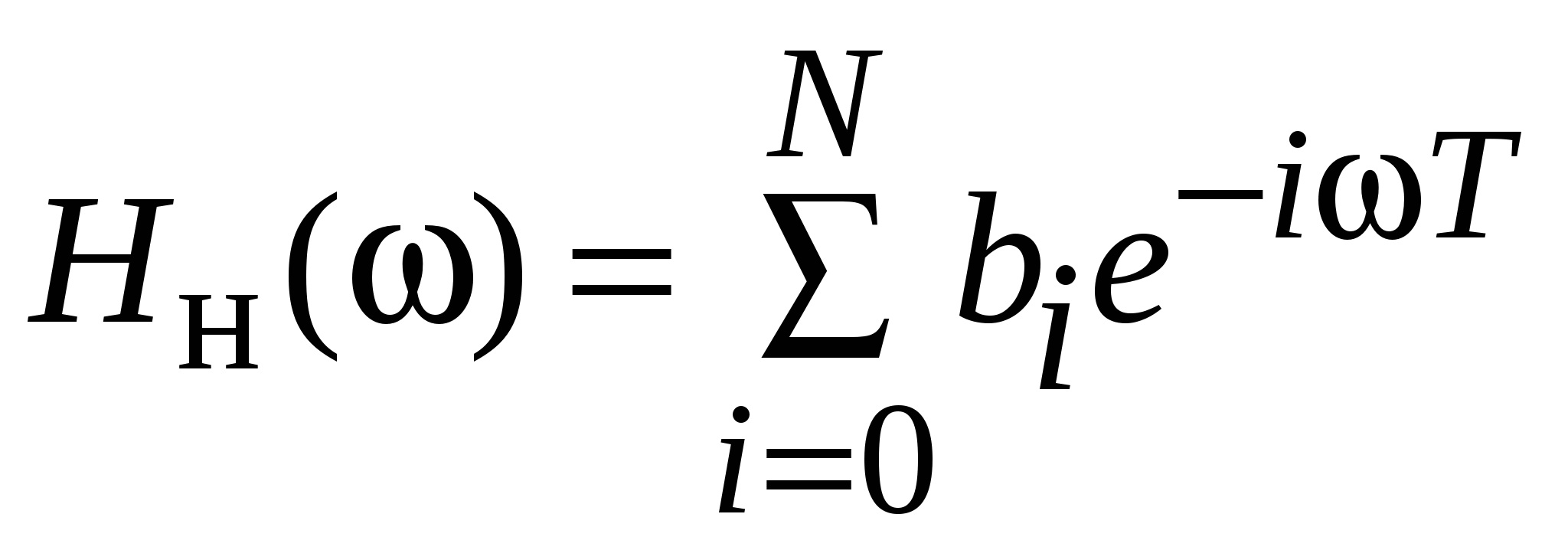

БИХ-фильтры. Методы синтеза

Фильтром с бесконечной импульсной характеристикой (БИХ-фильтром) называют фильтр, длина импульсной характеристики которого не ограничена справа или слева.

Будем рассматривать БИХ-фильтры при условии, что они являются физически реализуемыми и устойчивыми. Для импульсных характеристик таких фильтров h(n) справедливы следующие ограничения: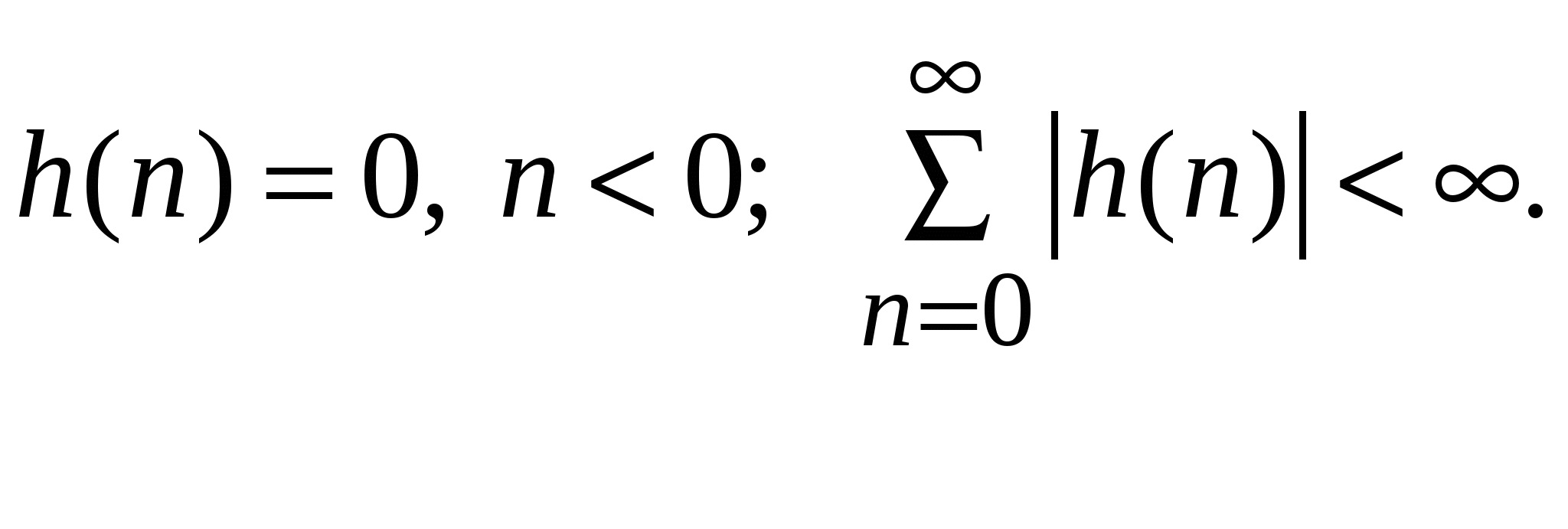

Наиболее общая форма записи z-преобразования импульсной характеристики БИХ-фильтров имеет вид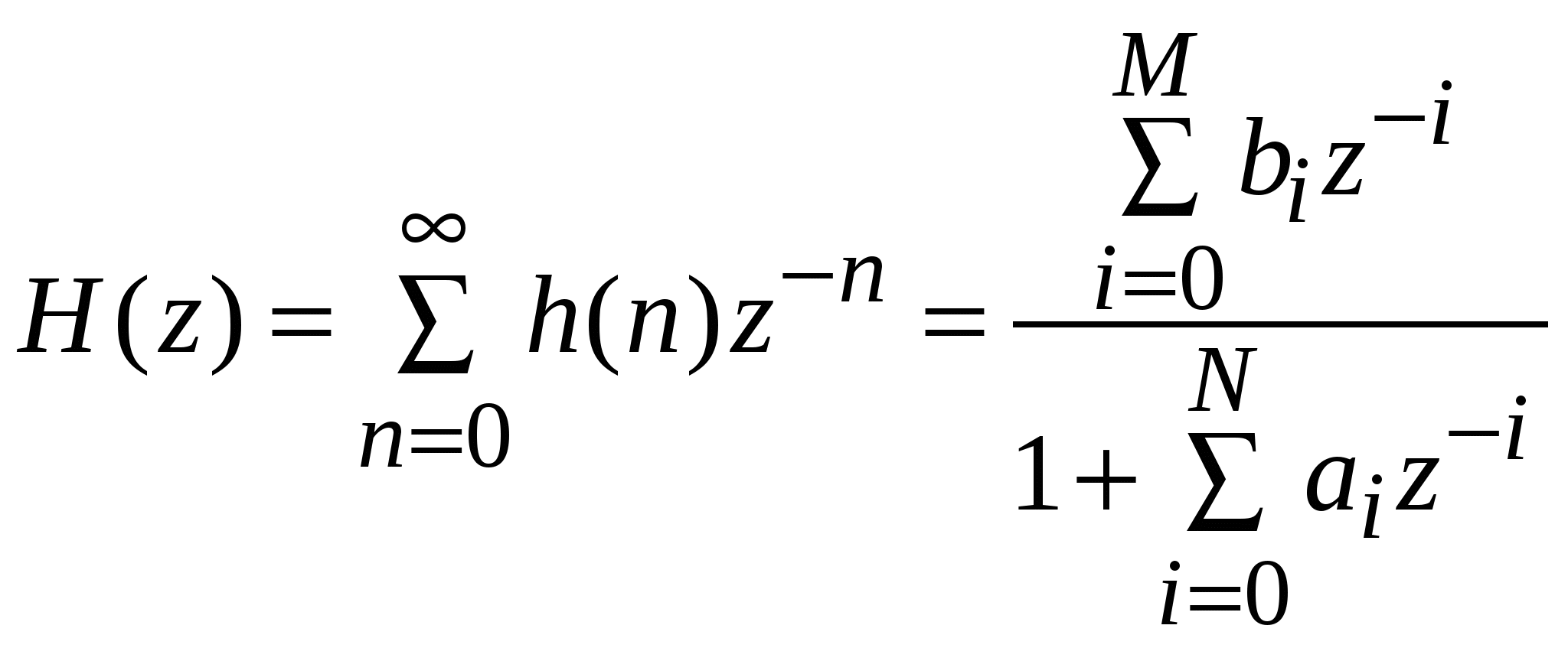

.

Предположим, что M £ N. Системы, удовлетворяющие этому условию, называют системами N-го порядка. Решение задачи расчета фильтров сводится к нахождению значений его коэффициентов a_i и b_i, обеспечивающих аппроксимацию заданных характеристик фильтра. Таким образом, задача расчета фильтра в значительной степени сводится к задаче аппроксимации и может быть решена чисто математическими методами.

Наиболее распространенным методом расчета цифровых БИХ-фильтров является метод дискретизации аналогового фильтра, удовлетворяющего заданным требованиям. При расчете цифровых фильтров верхних частот, полосовых и режекторных, используются два подхода, представленные на рисунке.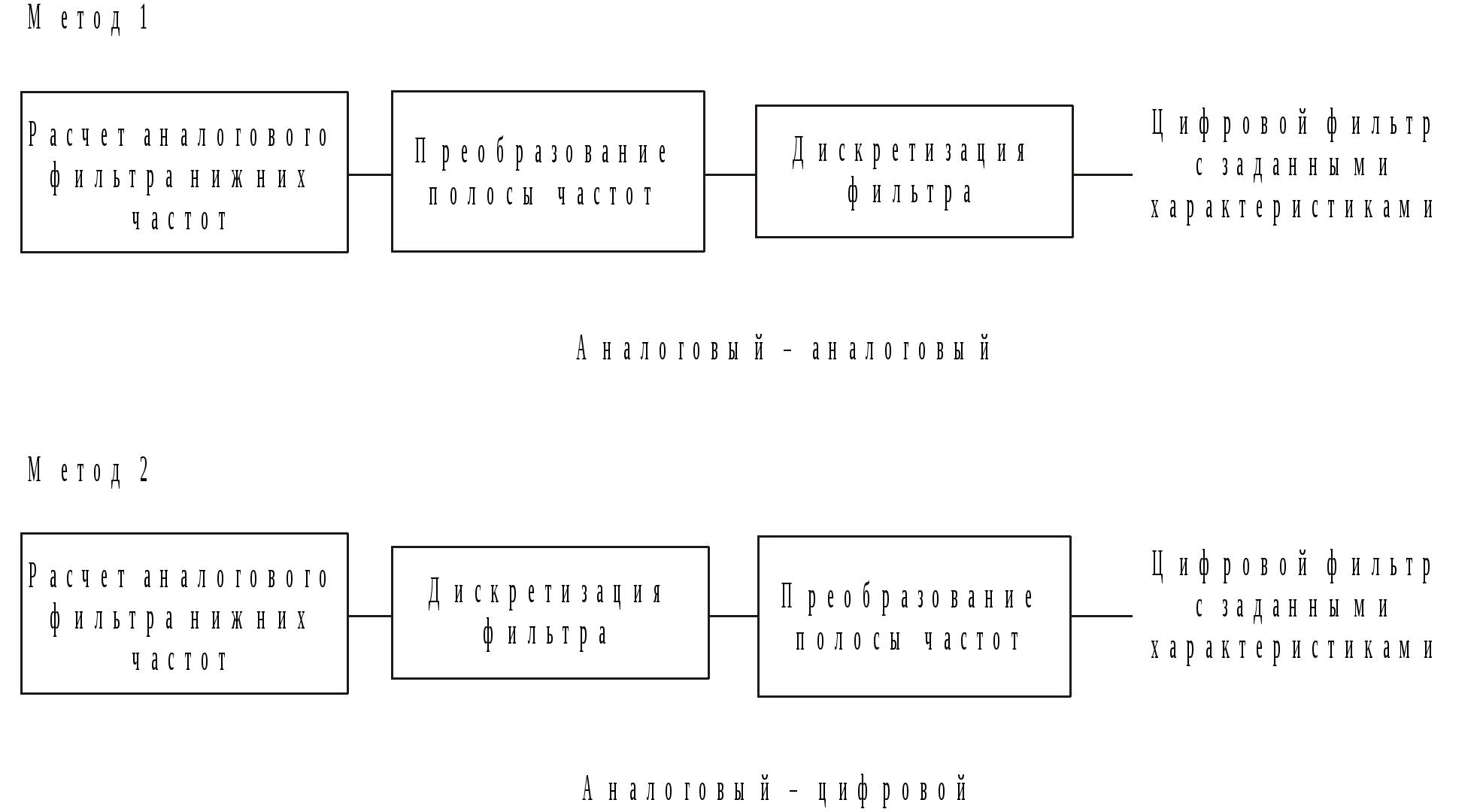

В первом случае нормализованный аналоговый фильтр предварительно преобразуется в другой аналоговый фильтр, из которого путем дискретизации рассчитывается фильтр с заданными характеристиками. Во втором случае нормализованный фильтр нижних частот дискретизуется сразу же, а затем преобразованием его полосы частот формируется цифровой фильтр с заданными характеристиками.

Обобщенное окно Хэмминга

Формула обобщенного окна Ханнинга имеет вид

причем,

лежит в пределах 0 £ a £ 1. Случай

= 0.5 соответствует окну Ханнинга.

Проектирование БИХ-фильтров

FIR1 – фильтр FIR проектируется с использованием метода окна:

B = FIR1(N,Wn) проектирует НЧ цифровой фильтр FIRN-го порядка и возвращает коэффициенты в векторе B длиной N + 1. Частота среза Wn должна быть между 0 < Wn < 1.0, с 1.0 соответствует половине частоты дискретизации.

Если Wn – двухэлементный вектор, Wn = [W1 W2], FIR1 возвращает полосовой фильтр порядка N с полосой W1 < W < W2. B = FIR1(N,Wn,'high') проектирует ВЧ-фильтр. B=FIR1(N,Wn,'stop') проектирует фильтр с полосой задержки, если Wn = [W1 W2]. Для высокочастотных и фильтров с полосой задержки N должно быть четным.

По умолчанию FIR1 использует окно Хэмминга. Другие представленные окна, включая прямоугольное (Boxcar), Хэмминга, Бартлетта, Блэкмана, Кайзера и Чебышева (Chebwin), могут быть определены с помощью необязательных аргументов. Например, B=FIR1(N,Wn,bartlett(N+1)) использует окно Бартлетта. B=FIR1(N,Wn,'high',chebwin(N+1,R)) использует окно Чебышева.

FILTER – цифровой фильтр:

Y = FILTER(B, A, X) фильтрует данные вектора X с фильтром, описанным векторами A и B для создания фильтрованных данных Y. Фильтр – реализация прямой формы 2 стандартного разностного уравнения

y(n) = b(1)*x(n) + b(2)*x(n–1) + ... + b(nb+1)*x(n–nb)

– a(2)*y(n–1) – ... – a(na+1)*y(n–na);

[Y, Zf] = FILTER(B,A,X,Zi) дает доступ к начальному и конечному состояниям задержек Zi и Zf.

3. Генерация входной последовательности сигнала
1. Сигнал составленный из подпоследовательностей различной частоты (3, 7, 10, 25Гц) с равным числом периодов задания подпоследовательностей сигнала
Сгенерируем сигнал составленный из подпоследовательностей различной частоты (3, 7, 10, 25Гц) с равным числом периодов задания подпоследовательностей сигнала с помощью средств программы MatLab и построим график полученного сигнала:
Fs=128; % частота дискретизации

T=4; % время реализации

n=512; % длина реализации

indx=(0:n-1); % вектор целых чисел от 0 до 511

% генерация входной последовательности сигнала

A=500; % амплитуда

t1=(0:127)/Fs; % интервал реализации для 1 подпоследовательности

t2=(128:255)/Fs; % интервал реализации для 2 подпоследовательности

t3=(255:384)/Fs; % интервал реализации для 3 подпоследовательности

t4=(385:511)/Fs; % интервал реализации для 4 подпоследовательности

y1=A*sin(3*t1*2*pi); % 1 подпоследовательность

y2=A*sin(7*t2*2*pi); % 2 подпоследовательность

y3=A*sin(10*t3*2*pi); % 3 подпоследовательность

y4=A*sin(25*t4*2*pi); % 4 подпоследовательность

t=[t1 t2 t3 t4]; % шаг дискретизации

y=[y1 y2 y3 y4]; % входной сигнал

figure(1);

clf, plot(t,y);

grid on;

ylabel('Amplitude (mkV)');

xlabel('Time');

title('Input signal');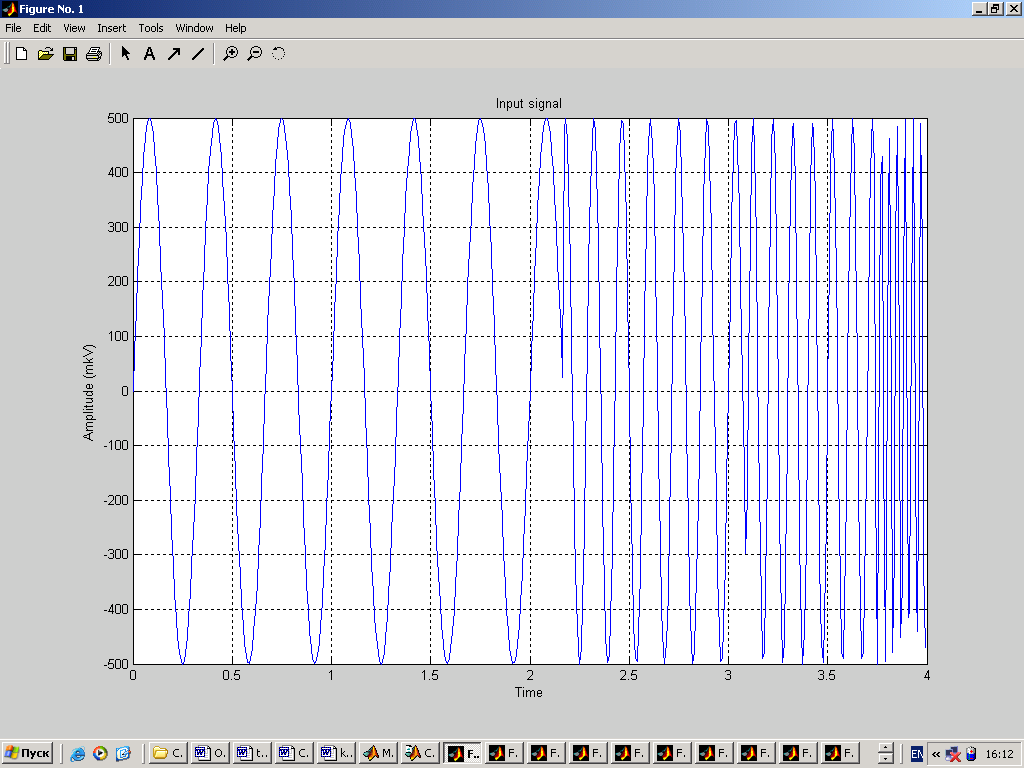

Реальный сигнал

Введем реальный сигнал из файла. Но в связи с тем, что реальный сигнал в файле записан с частотой 256Гц (а это в два раза больше используемой нами частотой), то значения будут считываться из файла через одно.
% реальный сигнал

fid=fopen('C:\Documents and Settings\Dinara\Рабочий стол\ЦОС\kursov\Signal.D05','r');

yf=fread(fid,n,'bit16',16);

fclose(fid);

figure(2);

clf,plot(t,yf);

grid on;

ylabel('Amplitude (mkV)');

xlabel('Time');

title('Real signal');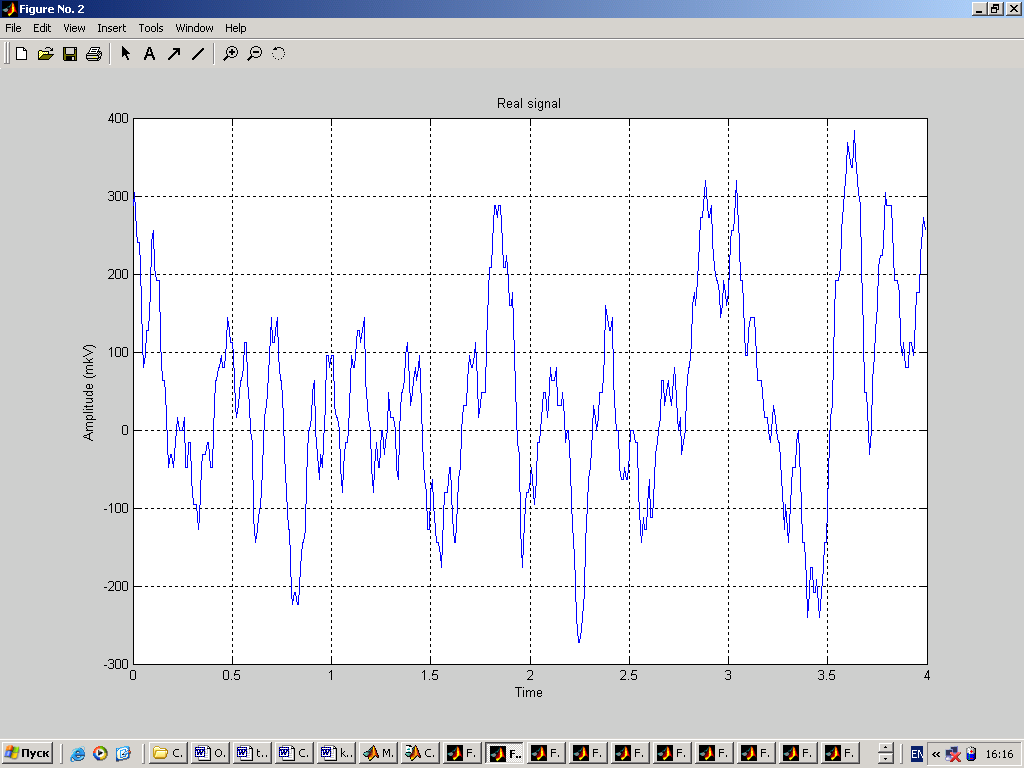

4. Реализация спектрального анализа с использованием БПФ
Произведем спектральный анализ данных сигналов. Для того, чтобы избежать явления Гибсона, исходный сигнал умножается на функцию окна. В данном случае будем использовать треугольное окно и окно Хэмминга.

На графиках построены спектры входных сигналов, умноженные на функцию окна.
Окно Чебышева:
% окно Чебышева

window1=chebwin(n,r);
% спектр входного сигнала с использованием окна Чебышева

FT=fft(window1.*y');

FT=FT(1:n/2);

figure(3);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum (triangle win)');

На графике видно, что фундаментальная частота нашего сигнала находится в районе 3 Гц. Но сигнал немного зашумлен.
% спектр реального сигнала с использованием окна Чебышева

FT=fft(window1.*yf);

FT=FT(1:n/2);

figure(4);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum of real signal (triangle win)');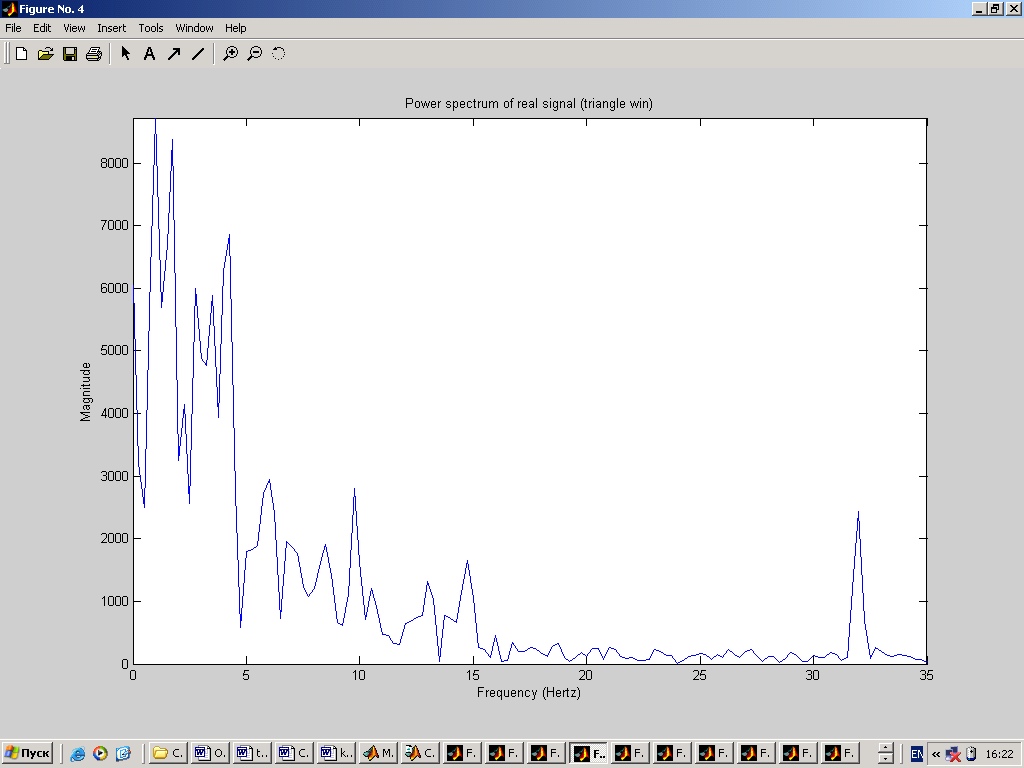

Здесь трудно определить, что это за сигнал, так как он слишком зашумлен. Но ориентировочно можно сказать, что фундаментальная частота находится в районе 1Гц.
Окно Ханнинга:
% окно Ханнинга

window2=hanning(n);
% спектр входного сигнала с использованием окна Ханнинга

FT=fft(window2.*y');

FT=FT(1:n/2);

figure(5);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum (hamming win)');

% спектр реального сигнала с использованием окна Ханнинга

FT=fft(window2.*yf);

FT=FT(1:n/2);

figure(6);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum of real signal (hamming win)');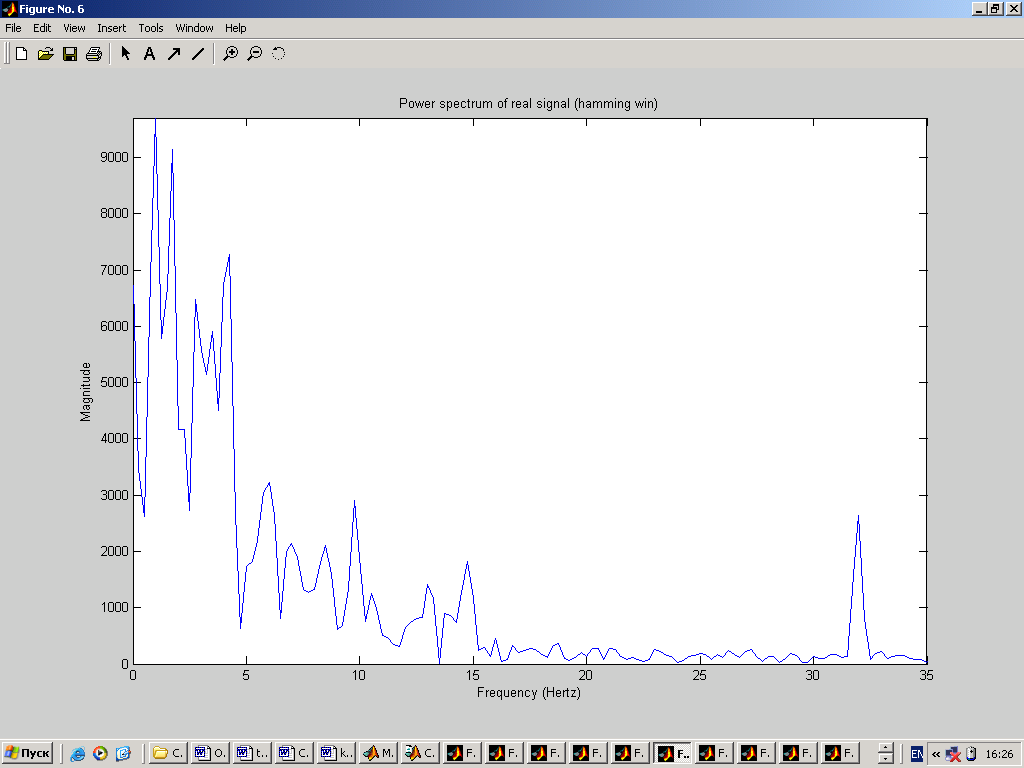

5. Проектирование и реализация ЦФ
Синтез низкочастотного БИХ-фильтра с использованием окна Чебышева 1 рода:
% проектирование и реализация ЦФ

Ws=25; % частота пропускания

Wn = (Ws/Fs)*2; % частота среза

len = 21; % длина фильтра

[b,a] = CHEBY1(len,0.5,Wn);% проектирование НЧ-фильтра Чебышева 1 рода

[H,F] = freqz(b,a,n,Fs);

figure(7);

clf, plot (F,abs(H));

ylabel('Magnitude')

xlabel('Frequency (Hertz) ')

title('Filter Response')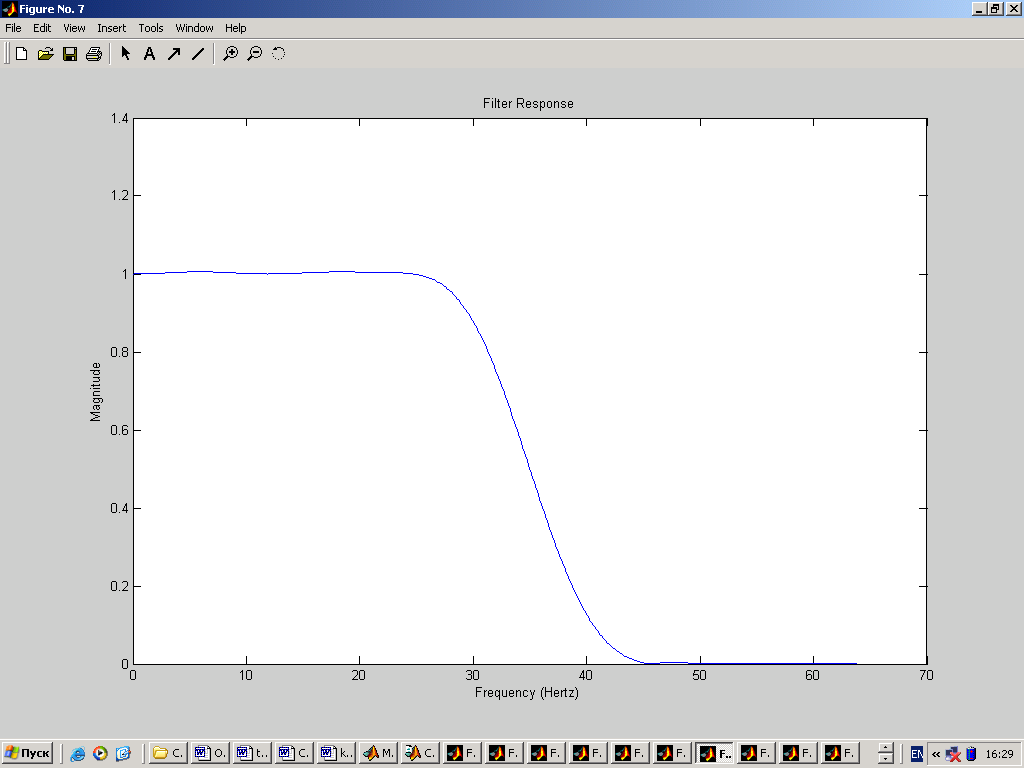

Теперь проведем фильтрацию заданных сигналов.
% фильтрация входного сигнала

format long e

fily=filter(b,1,y);

figure(8);

clf, plot(t,fily);

ylabel('Amplitude (mkV)');

xlabel('Time');

title('Input signal after filtration');

Определим частотный спектр отфильтрованного сигнала:
% спектр отфильтрованного входного сигнала

FT=fft(window1.*fily');

FT=FT(1:n/2);

figure(9);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum after filtration');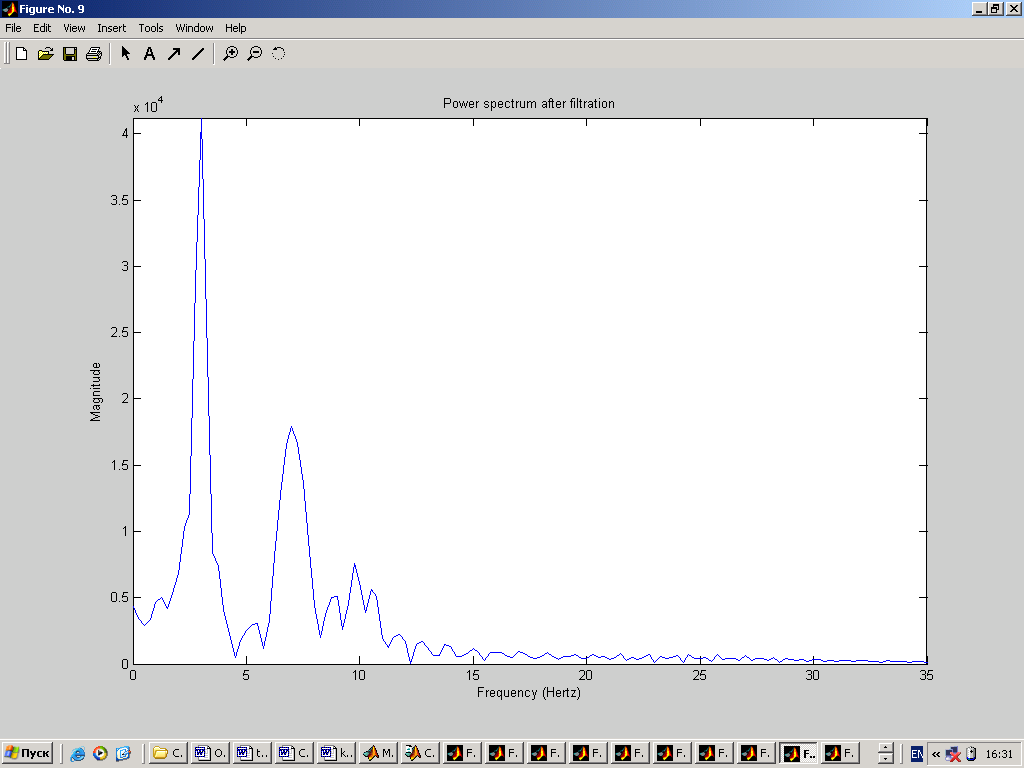

Аналогично для реального сигнала:
% фильтрация реального сигнала

filyf=filter(b,1,yf');

figure(10);

clf, plot(t,filyf);

ylabel('Amplitude (mkV)');

xlabel('Time');

title('Real signal after filtration');

% спектр отфильтрованного реального сигнала

FT=fft(window1.*filyf');

FT=FT(1:n/2);

figure(11);

clf, plot(step,abs(FT));

axis([0 25 0 max(abs(FT))]);

ylabel('Magnitude');

xlabel('Frequency (Hertz)');

title('Power spectrum of real signal after filtration');

В связи с тем, что сигналы плохо отфильтрованы, то попробуем изменить полосу пропускания фильтра (возьмем её равной 15Гц).
% проектирование и реализация ЦФ

Ws=15; % частота пропускания

Wn = (Ws/Fs)*2; % частота среза

len = 21; % длина фильтра

[b,a] = CHEBY1(len,0.5,Wn);% проектирование НЧ-фильтра Чебышева 1 рода

[H,F] = freqz(b,a,n,Fs);figure(7);

clf, plot (F,abs(H));

ylabel('Magnitude')

xlabel('Frequency (Hertz) ')

title('Filter Response')

Тогда сигналы и их спектры будут иметь следующий вид.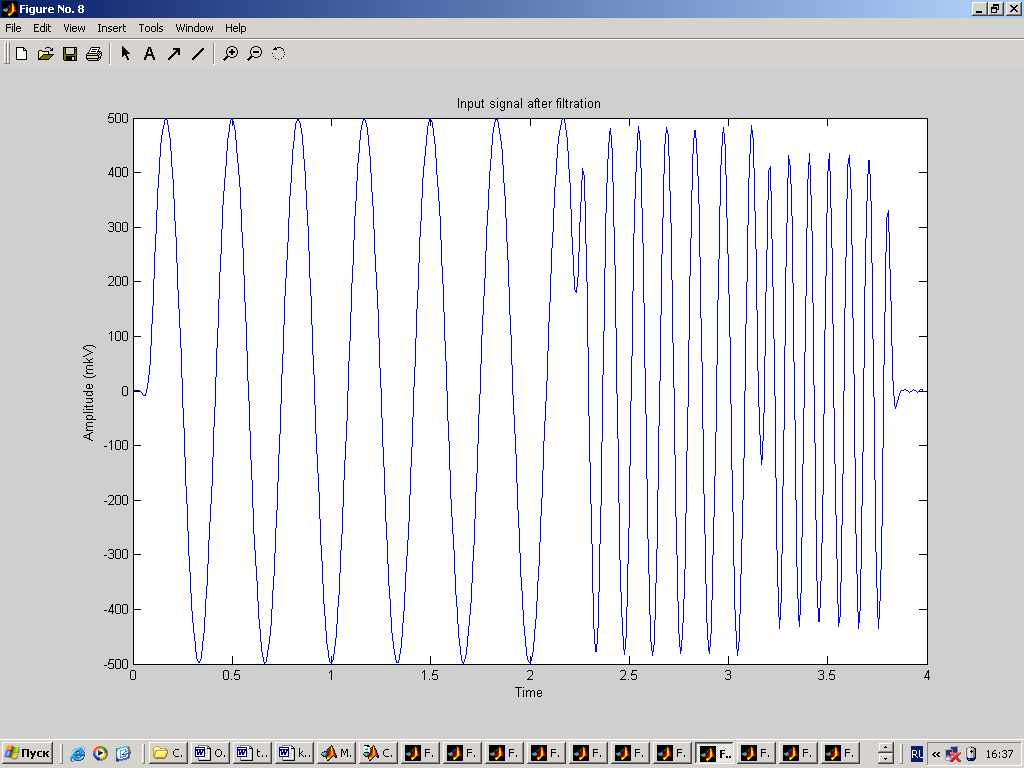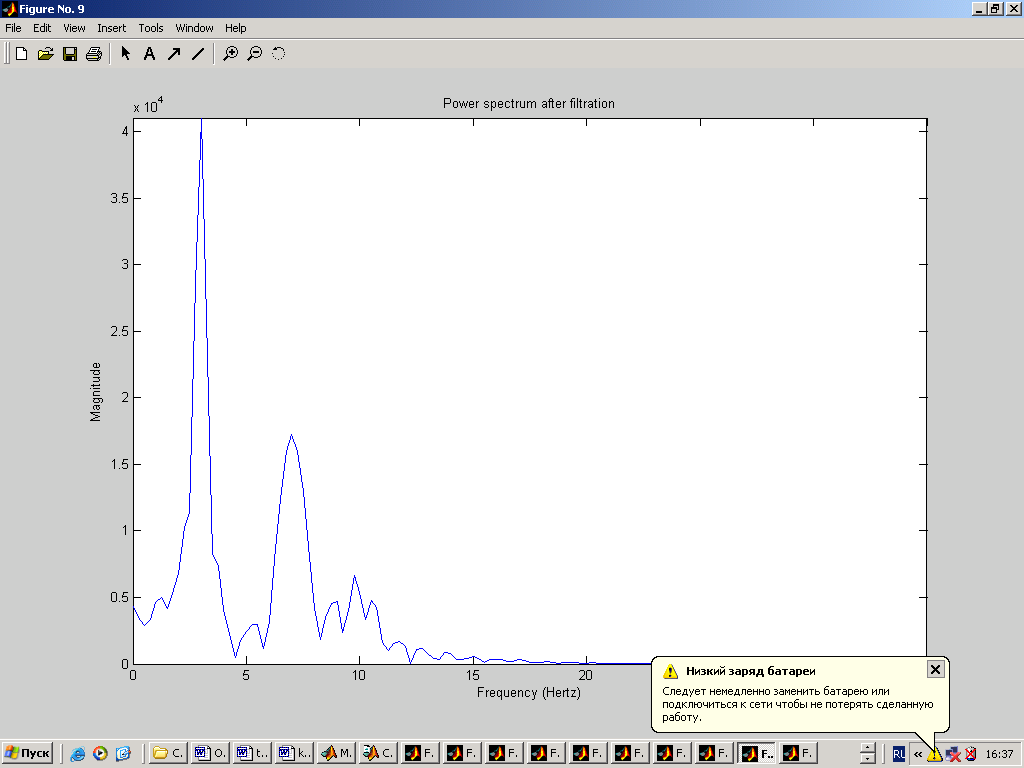

Попробуем теперь взять частоту пропускания равной 5Гц.
% проектирование и реализация ЦФ

Ws=5; % частота пропускания

Wn = (Ws/Fs)*2; % частота среза

len = 21; % длина фильтра

[b,a] = CHEBY1(len,0.5,Wn);% проектирование НЧ-фильтра Чебышева 1 рода

[H,F] = freqz(b,a,n,Fs);

figure(7);

clf, plot (F,abs(H));

ylabel('Magnitude')

xlabel('Frequency (Hertz) ')

title('Filter Response')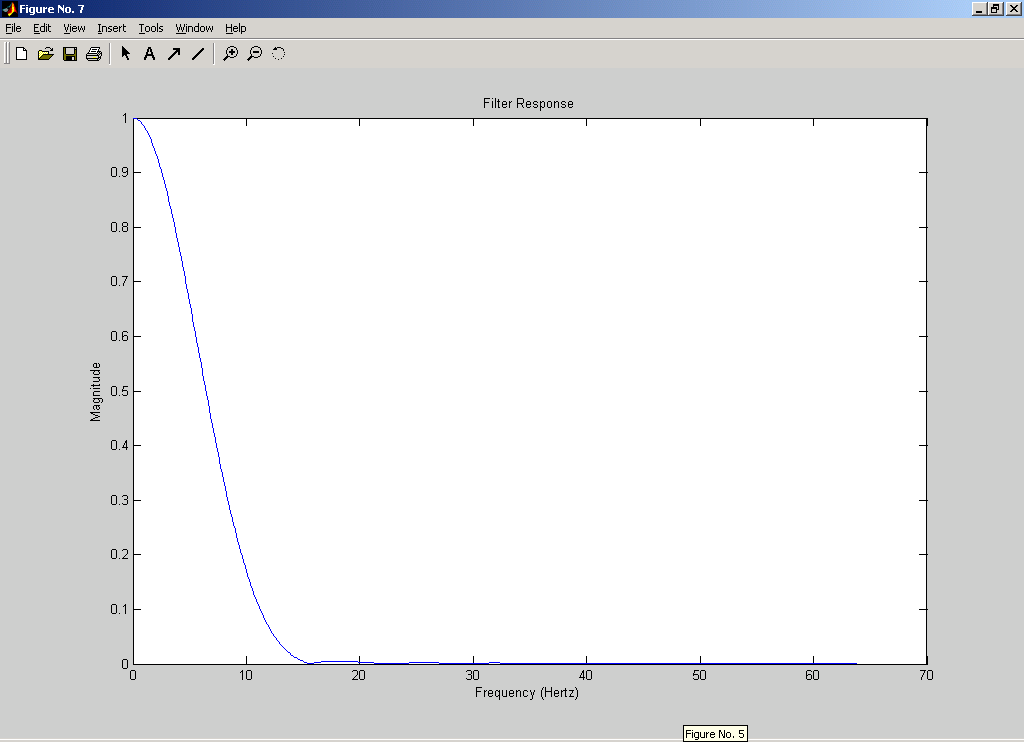

Тогда сигналы и их спектры будут иметь следующий вид.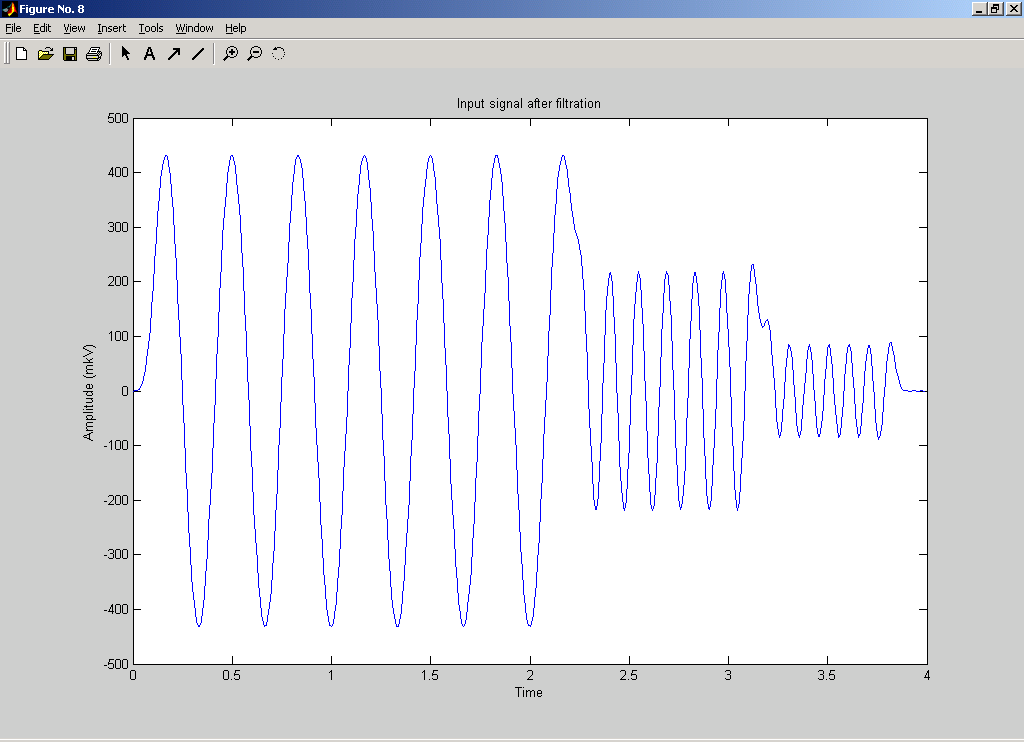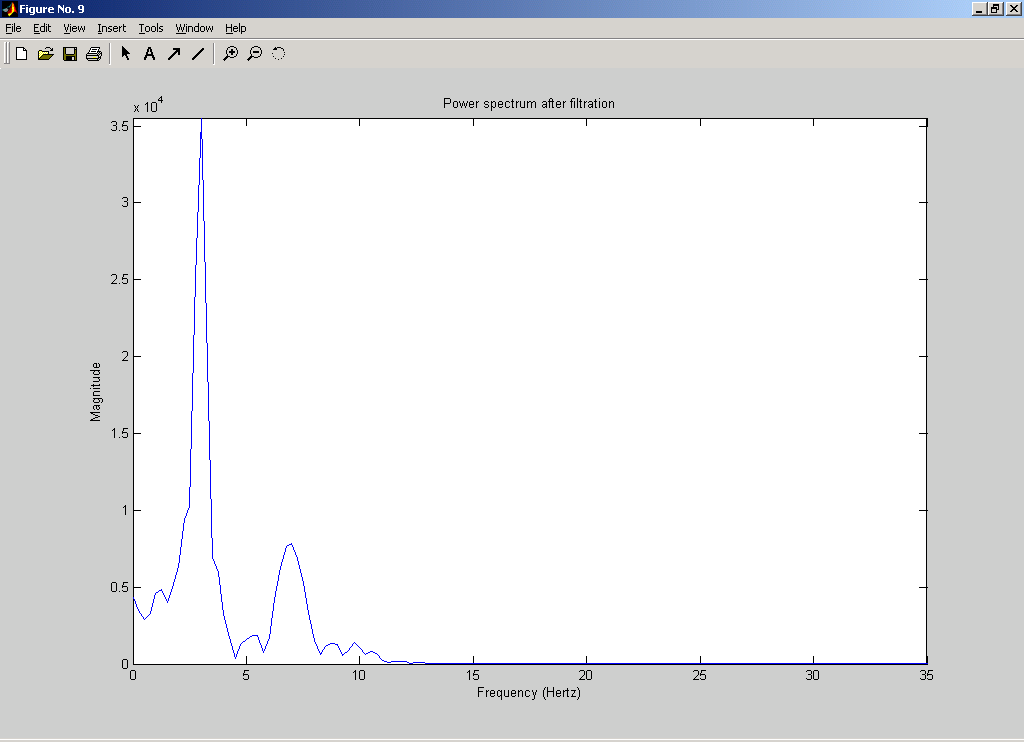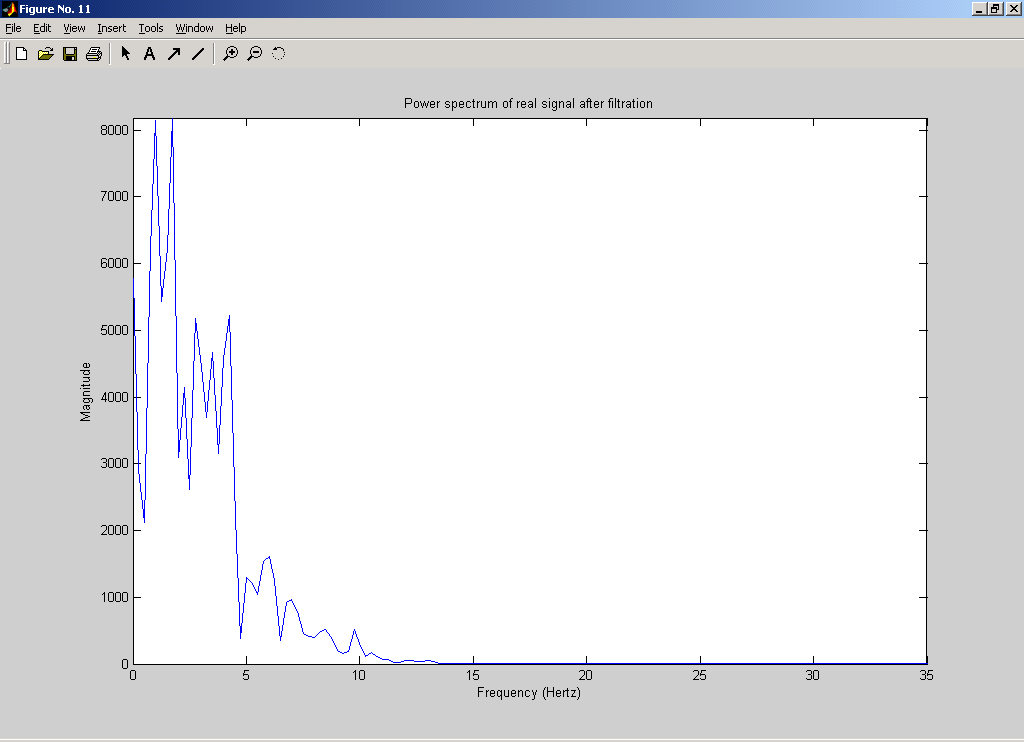

6. Вывод
В ходе курсовой работы были получены навыки работы в среде MatLab: генерация входного сигнала, считывание сигнала из файла, построение спектральных функций сигналов с применением функций окон, а также построение НЧ-фильтра и фильтрация с помощью него исходного сигнала.

Проанализировав графики спектральных функций исходного сигнала и реального сигнала можно заметить, что реальный сигнал является более зашумленным. По графику спектральной функции исходного сигнала можно четко определить его частотные характеристики, когда как по реальному сигналу это сделать однозначно нельзя.