Гидравлика, Гидростатика Теория и примеры решения типовых задач. Гидравлика. Гидростатика

• Название: Гидравлика. Гидростатика
• Анкор: Гидравлика, Гидростатика Теория и примеры решения типовых задач.doc
• Дата: 27.04.2017
• Размер: 0.59 Mb.
• Имя файла: Гидравлика, Гидростатика Теория и примеры решения типовых задач.doc
• Тип: Реферат; #6101
• Категория: Промышленность. Энергетика
• страница: 1 из 3

Гидравлика. Гидростатика

Сборник типовых задач

СОДЕРЖАНИЕ

Введение

1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ

1.1 Сведения из теории

1.1.1 Плотность

1.1.2. Удельный вес

1.1.3. Коэффициент объемного сжатия

1.1.4. Коэффициент температурного расширения

1.1.5. Вязкость

1.2. Примеры решения задач

1.3 Задания для расчетно-графических работ

2 ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ

2.1 Сведения из теории

2.1.1 Основное уравнение гидростатики

2.1.2 Давление при абсолютном покое

2.1.3 Поверхность уровня при абсолютном покое

2.1.4 Анализ основного уравнения гидростатики

2.1.5 Пьезометрическая и вакуумметрическая высоты

2.1.6 Условия равновесия жидкости в сообщающихся сосудах

2.1.7 Понятие напора. Удельная потенциальная энергия

2.2 Примеры решения задач

2.3 Задания для расчетно-графических работ

3 ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ

3.1 Сведения из теории

3.1.1 Относительный покой при прямолинейном движении на наклонной плоскости

3.1.2 Относительный покой при вращении вокруг вертикальной оси

3.2 Примеры решения задач

3.3 Задания для расчетно-графических работ

ПРИЛОЖЕНИЕ 1 Некоторые физические свойства жидкостей при давлении 0,1 Мпа

ПРИЛОЖЕНИЕ 2. Кинематическая вязкость масел при различных температурах

ПРИЛОЖЕНИЕ 3Динамическая вязкость масел при различных температурах

ПРИЛОЖЕНИЕ 4

Введение

Основное назначение сборника – дать студентам материал, который позволит выработать навыки применения теоретических сведений к решению конкретных задач технического характера и тем самым освоить практику гидравлических расчётов.

Данный курс является основной теоретической дисциплиной для специальностей 2903, 2908, 2909, 1507, 1709.

Данный сборник содержит задачи по гидростатике и включает разделы: “Физические свойства жидкости”, “Гидростатическое давление” и “Относительный покой жидкости”.

Каждый раздел сборника содержит достаточно полные сведения из теории, касающейся материала данного раздела, методические указания и примеры решения некоторых типовых задач.

В четырёх приложениях даются материалы справочного характера, которые необходимы для решения задач.

Наличие в сборнике обширного и разнообразного материала позволяет составить индивидуальное задание для каждого студента.

После ознакомления с соответствующим теоретическим материалом и методическими указаниями по решению типовых задач, следует переходить к самостоятельному выполнению полученного задания.

Каждое задание состоит из нескольких задач, номера и варианты которых выдаются преподавателем. Задание выполняется на листах формата А4, необходимые чертежи выполняются с соблюдением выбранного масштаба.

1. ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ

1.1. Сведения из теории

Жидкостью называется физическое тело, обладающее двумя отличительными особенностями: незначительным изменением своего объема под действием больших внешних сил и текучестью, легкоподвижностью, т.е. изменением своей формы под действием даже незначительных внешних сил. Одной из основных механических характеристик жидкости является плотность.

1.1.1. Плотность.

Плотностью  (кг/м³) называется масса единицы объема жидкости:

,                                                                                                                      (1.1)

гдеm – масса жидкого тела, кг; W – объем, м³.

Плотность жидкостей уменьшается с увеличением температуры. Исключение представляет вода в диапазоне температур от 0 до 4 ⁰С, когда ее плотность увеличивается, достигая наибольшего значения при температуре 4 ⁰С  = 1000 кг/м³.

1.1.2. Удельный вес

Удельным весом  (Н/м³) жидкости называется вес единицы объема этой жидкости:

,                                                                                                                          (1.2)

где G – вес жидкого тела, Н; W – объем, м³.

Для воды при температуре 4 ⁰С g = 9810 Н/м³.

Между плотностью и удельным весом существует связь:

,                                                                                                                      (1.3)

где g – ускорение свободного падения, равное 9,81 м/с².

Сопротивление жидкостей изменению своего объема под действием давления и температуры характеризуется коэффициентами объемного сжатия и температурного расширения.

1.1.3. Коэффициент объемного сжатия

Коэффициент объемного сжатия  _w (Па^-1) – это относительное изменение объема жидкости при изменении давления на единицу: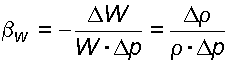

,                                                                                          (1.4)

где  W – изменение объема W;   – изменение плотности  , соответствующие изменению давления на величину  p.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкостейE_ж (Па)

.                                                                                                                  (1.5)

Значение модуля упругости жидкостей зависит от давления и температуры. Если принять, что приращение давления , а изменение объема то:

;                                                                                              (1.6)

.                                                                                                  (1.7)

1.1.4. Коэффициент температурного расширения

1. 
   Коэффициент температурного расширения  _t (⁰С)^-1, выражает относительное изменение объема жидкости при изменении температуры на один градус:
   

,                                                                                                                  (1.8)

где  W – изменение объема W, соответствующее изменению температуры на величину  t.

Коэффициент температурного расширения воды увеличивается с возрастанием температуры и давления; для большинства других капельных жидкостей  _t с увеличением давления уменьшается. Если принять, что приращение температуры  t = t – t₀, а изменение объема

 W = W – W₀ , то:

;                                                                                                  (1.9)

.                                                                                                      (1.10)

1.1.5. Вязкость

     Вязкостью называется свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Вязкость проявляется только при движении жидкости и сказывается на распределении скоростей по живому сечению потока (рис. 1.1).

С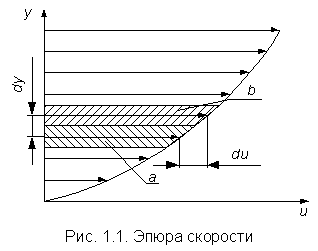огласно гипотезе Ньютона сила внутреннего трения F в жидкостях пропорциональна градиенту изменения скорости , площади соприкосновенияслоев S, зависит от рода жидкости и очень незначительно зависит от давления.

,                                                  (1.11)                                                                                                                           

где S – площадь соприкасающихся слоев, м²; du – скорость смещения слоя "b" относительно слоя "a", м/с;dy – расстояние, на котором скорость движения слоев изменилась на du, м; – градиент скорости, изменение скорости по нормали к направлению движения (с^-1);  – коэффициент динамической вязкости (Па  с).

Если силу трения F отнести к единице площади соприкасающихся слоев, то получим величину касательного напряжения  , и тогда (1.11) примет вид:

.                                                                                                                  (1.12)

Из (1.12) следует, что коэффициент динамической вязкости может быть определен как:

.                                                                                                                  (1.13)

Из (1.13) нетрудно установить физический смысл коэффициента динамической вязкости. При градиенте скорости = 1; =  и выражает силу внутреннего трения, приходящуюся на единицу площади поверхности соприкасающихся слоев жидкости.

В практике, для характеристики вязкости жидкости, чаще применяют не коэффициент динамической вязкости, а коэффициент кинематической вязкости  (м²/с). Коэффициентом кинематической вязкости называется отношение коэффициента динамической вязкости к плотности жидкости:

.                                                                                                                          (1.14)

Вязкость жидкости зависит от рода жидкости, от температуры и от давления.

Зависимость вязкости минеральных масел, применяемых в гидросистемах, от давления p при возрастании его до 50 МПа, можно определять с помощью приближенной эмпирической формулы:

,                                                                                                      (1.15)

где  _pи– кинематическая вязкость соответственно при давлении p и 0,1 МПа;K – опытный коэффициент, зависящий от марки масла: для легких масел ( ₅₀ < 15 10^-6м²/с)К = 0,02, для тяжелых масел ( ⁵⁰ > 15 10^-6м²/с)К = 0,03. При незначительных давлениях изменением вязкости пренебрегают. С повышением температуры вязкость жидкости уменьшается. Зависимость коэффициента кинематической вязкости от температуры определяется по эмпирической формуле: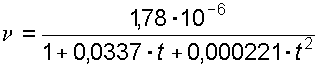

.                                                                          (1.16)

Для смазочных масел, применяемых в машинах и гидросистемах, рекомендуется следующая зависимость:

,                                                                                                          (1.17)

где  _t – кинематическая вязкость при температуре t; ₅₀ – кинематическая вязкость при температуре 50⁰С; n – показатель степени, зависящий от  ₅₀, определяемый по формуле:

.                                                                                              (1.18)

Вязкость жидкости определяют при помощи вискозиметра Энглера и выражают в градусах Энглера (⁰Е). Градус Энглера (⁰Е) есть отношение времени истечения испытуемой жидкости ко времени истечения дистиллированной воды. Для перехода от вязкости в градусах Энглера к коэффициенту кинематической вязкости  применяется формула Убеллоде: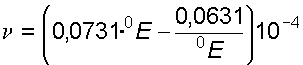

.                                                                          (1.19)

Вязкость также определяют капиллярным вискозиметром Оствальда. Коэффициент кинематической вязкости в этом случае определяют по формуле:

,                                                                                                     (1.20)

где с – постоянная прибора; T_ж – время истечения жидкости, с.

.2. Примеры решения задач

Пример 1. Удельный вес бензина  = 7063 Н/м³. Определить его плотность.

Решение. ; ;  = 7063 / 9,81 = 720 кг/м³.

Пример 2. Плотность дизельного мазута = 878 кг/м³. Определить его удельный вес.

Решение. ;  = 878  9,81 = 8613 H/м³.

 

Пример 3. Медный шар d = 100 мм весит в воздухе 45,7 H, а при погружении в жидкость 40,6 H. Определить плотность жидкости.

Решение. Определяем вес G и объем W вытесненной жидкости

G = G_в- G_ж; G = 45,7 – 40,6 = 5,1 H.

; W = 3,14 0,1³ / 6 = 0,523 10^-3 м³; находим плотность жидкости

;; = 5,1 / (9,81 0,52310^-3) кг/м³.

Пример 4. Трубопровод диаметром d = 500 мм и длинойL = 1000 м наполнен водой при давлении 400 кПа, и температуре воды 5⁰C. Определить, пренебрегая деформациями и расширением стенок труб, давление в трубопроводе при нагревании воды в нем до 15 ⁰C, если коэффициент объемного сжатия _w = 5,18 10^-10 Па^-1, а коэффициент температурного расширения _t = 150 10^-60С^-1.

Решение. Находим объем воды в трубе при t = 5 ⁰C

; W = 0,785 0,5²  1000 = 196,25 м³; находим увеличение объема W при изменении температуры

; ;

W = 196,25 10 150 10^-6 = 0,29м³;находим приращение давления в связи с увеличением объема воды

;p = 0,29 / (196,25 5,18 10^-10) = 2850 кПа; давление в трубопроводе после увеличения температуры

400 кПа + 2850 кПа = 3250 кПа = 3,25 МПа.

 

Пример 5. Вязкость нефти, определенная по вискозиметру Энглера, составляет 8,5 ⁰Е. Определить динамическую вязкость нефти, если ее плотность  = 850 кг/м³.

Решение. Находим кинематическую вязкость по формуле Убеллоде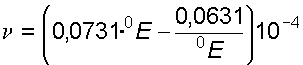

;

 = (0,0731 8,5 – 0,0631/8,5) 10^-4=6,14 10^-5 м²/с;

находим динамическую вязкость нефти

;  = 0,614 10^-4 850 = 0,052 Па с.

 

Пример 6. Определить коэффициент динамической и кинематической вязкости воды, если шарик d = 2 мм из эбонита с  = 1,2 10³ кг/м³ падает в воде с постоянной скоростью u = 0,33 м/с. Плотность воды =10³ кг/м³.

Решение. При движении шарика в жидкости с постоянной скоростью сила сопротивления равняется весу шарика. Сила сопротивления определяется по формуле Стокса:

.

Вес шарика определяется по формуле

.

Так как G=F ,то

.

Следовательно, коэффициент динамической вязкости определится

;  = 1,2 10³  9,81 (2 10^-3)² / (18 0,33) = 0,008 Па с.

Коэффициент кинематической вязкости

;

 = 0.008 / 10³ = 8 10^-6 м²/с.

 

Пример 7. При гидравлическом испытании системы объединенного внутреннего противопожарного водоснабжения допускается падение давления в течение 10 мин. на p = 4,97104 Па. Определить допустимую утечку W при испытании системы вместимостью W = 80 м³.
Коэффициент объемного сжатия _w= 5 10^-10Па^-1.

Решение. Допустимую утечку W определяем из формулы

;                              ;

W = 5 10^-10 80  4,9 10⁴ = 1,96 10^-3 м³.

2. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ

2.1. Сведения из теории

На жидкость, находящуюся в состоянии покоя, действуют силы, которые можно разделить на поверхностные и массовые.

Поверхностные силы приложены к частицам жидкости, находящимся на поверхности раздела данной жидкости и другой среды (реакция стенки сосуда, сила давления поршня, сила давления газа на свободную поверхность).

Массовые силы воздействуют на все частицы данного объема жидкости и пропорциональны массе каждой частицы (силы тяжести, силы инерции, центробежные силы).

Основным понятием гидростатики является понятие гидростатического давления.

Выделим, в находящейся в равновесии жидкости, некоторый объем произвольной формы. Рассечем его на две части I и II плоскостью AB (рис. 2.1).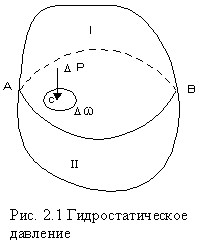

Воздействие части I жидкости на часть II будет передаваться по плоскости раздела AB. Выделим на плоскости раздела площадку площадью . Заменим воздействие части I на эту площадку силой . Сила воздействия , приходящаяся на эту площадку называется силой гидростатического давления.

Отношение силы к площади

                                                                                                                     (2.1)

представляет среднее гидростатическое давление.

Если площадь стремится к 0, то отношение будет стремиться к пределу, который называется гидростатическим давлением в точке

 

                                                                                                                    (2.2)

Гидростатическое давление направлено всегда по внутренней нормали к площадке, на которой это давление действует и является сжимающим напряжением, потому что в покоящейся жидкости не могут существовать касательные и растягивающие усилия. Величина гидростатического давления в любой точке жидкости по всем направлениям одинакова.

Гидростатическое давление зависит от положения рассматриваемой точки внутри жидкости и от внешнего давления, действующего на свободной поверхности жидкости. Гидростатическое давление имеет размерность напряжения, т.е.

. Измеряют давление в Н/м² (Паскаль). Атмосферное давление измеряют технической атмосферой равной 98100 Па или физической равной 101325 Па, иногда используется единица бар (1бар=10⁵Па).

Различают давление абсолютное (иногда употребляют термин ‘’полное‘’) и избыточное. Абсолютным называется давление, определённое с учетом атмосферного давления. Избыточное давление это давление сверх атмосферного, определенное без учета атмосферного.

;                                                           (2.3)

Абсолютное давление не может быть отрицательным, так как жидкость не воспринимает растягивающих напряжений . Избыточное давление может быть и больше и меньше нуля . Для удобства, отрицательное избыточное давление, взятое со знаком плюс, называют вакуумметрическим давлением

                                                                                                             (2.4)

Очень часто избыточное давление называют манометрическим, так как оно измеряется с помощью манометров, или пьезометрическим, так как оно измеряется с помощью пьезометров.

2.1.1. Основное уравнение гидростатики

В 1755 г. Л. Эйлером были получены дифференциальные уравнения равновесия жидкости: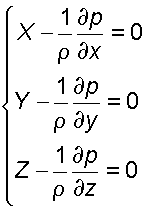

                                                                                                 (2.5)

где – градиенты давления в направлении соответствующих координатных осей; X, Y, Z – проекции единичных массовых сил на соответствующие координатные оси; - плотность жидкости.

После незначительных преобразований данную систему уравнений можно представить в виде уравнения

.                                                                              (2.6)

Полученное уравнение выражает изменение давления вдоль координатных осей в общем случае равновесия, и называется основным дифференциальным уравнением гидростатики.

Поверхностью уровня называется такая поверхность, во всех точках которой рассматриваемая функция имеет одно и то же значение. Для задач гидравлики особое значение имеет поверхность равного давления. Эту поверхность будем называть поверхностью уровня.

Так как во всех точках поверхности уровня гидростатическое давление одинаково, то есть ,то . Из основного дифференциального уравнения гидростатики имеем:

                                                                                 (2.7)

поскольку плотность не равна нулю,запишем

                                                                                     (2.8)

поверхность уровня имеет следующие свойства:

1) две поверхности уровня не пересекаются между собой;

2) массовые силы направлены нормально к поверхности уровня.

Поверхность уровня на границе жидкой и газообразной среды называется свободной поверхностью.

 

2.1.2. Давление при абсолютном покое

Рассмотрим случаи равновесия жидкости, находящейся в сосуде, в состоянии абсолютного покоя под действием сил тяжести и внешнего давления на свободной поверхности. В этом случае проекции единичной силы тяжести на координатные оси равны: .

После подстановки в уравнение (2.6) получаем

.                                                                                                               (2.9)

После интегрирования имеем

.                                                                                                      (2.10)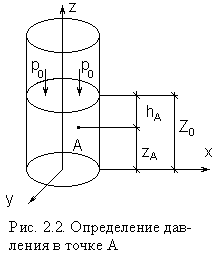

Постоянную интегрирования С находим из граничных условий
(рис. 2.2): при ;

.                                                                                          (2.11)

После совместного решения уравнений (2.6) и (2.7) получаем

.

или

                                                                                                     (2.12)

Полученное уравнение является основным уравнением гидростатики, позволяющие определять любое давление в точке.

2.1.3. Поверхность уровня при абсолютном покое

Дифференциальное уравнение поверхности уровня в этом случае имеет вид:

или                                                                                              (2.13)

интегрируя, находим

.                                                                                                              (2.14)

Так как - произвольная постоянная, то это уравнение будет уравнением семейства горизонтальных плоскостей. Таким образом, поверхность уровня есть горизонтальная плоскость, следовательно, и свободная поверхность будет горизонтальной плоскостью.

2.1.4. Анализ основного уравнения гидростатики

Как уже отмечалось, основное уравнение гидростатики служит для определения величины гидростатического давления в любой точке покоящейся жидкости

.                                                                                                          (2.15)

Анализируя основное уравнение гидростатики можно сделать следующие выводы:

1. 
   Гидростатическое давление есть сумма внешнего давления, действующего на свободной поверхности и весового давления, создаваемого весом столба жидкости высотой ;
   
2. 
   Внешнее давление не зависит от координат рассматриваемых точек, то есть оно передается во все точки покоящейся жидкости без изменения, поэтому жидкость используется как среда для передачи давления. На этом свойстве жидкости основано действие гидравлических машин (гидропрессы, силовые цилиндры, гидродомкраты);
   
3. 
   Весовое давление является функцией координат точки. С увеличением заглубления точки под свободную поверхность, давление возрастает;
   
4. 
   Внешнее давление может быть больше атмосферного, меньше атмосферного и равно атмосферному. Если численное значение определено с учетом атмосферного, то давление по формуле (2.15) будет абсолютным; если определено без учета атмосферного, то
   

будет избыточным.

2.1.5. Пьезометрическая и вакуумметрическая высоты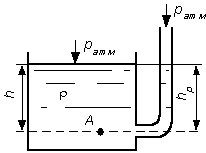

    Рис 2.3. Условие равновесия для открытого сосуда

Рассмотрим условия равновесия для открытого сосуда, заполненного жидкостью, к которому в точке А присоединена открытая сверху трубка (рис. 2.3). Под действием весового или избыточного давления , жидкость поднимается в трубке на высоту . Указанная трубка называется пьезометром, а высота – пьезометрической высотой.

Представим основное уравнение гидростатики относительно плоскости, проходящей через точку А. Давление в точке А со стороны сосуда определяется как:

                                                                                                 (2.16)

со стороны пьезометра:

                                                                                                 (2.17)

тогда:

                                                                         (2.18)

или

                                                                                                                             (2.19)

то есть пьезометрическая высота показывает величину избыточного давления в точке, где присоединен пьезометр в линейных единицах размерности.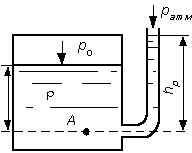

    Рис 2.4. Условие равновесия для закрытого сосуда

Рассмотрим условия равновесия теперь для закрытого сосуда, где давление на свободной поверхности p₀ больше атмосферного давления p_атм (рис. 2.4).

Под действием давления p₀ большего p_атм и весового давления жидкость поднимается в пьезометре на высоту большую, чем в случае открытого сосуда.

Давление в точке А со стороны сосуда:

                                                                                                     (2.20)

со стороны открытого пьезометра:

                                                                                                 (2.21)

тогда:

                                                                             (2.22)

из этого равенства получаем выражение для :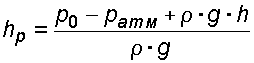

.                                                                                      (2.23)

Анализируя полученное выражение, устанавливаем, что и в этом случае пьезометрическая высота соответствует величине избыточного давления в точке присоединения пьезометра. В данном случае избыточное давление состоит из двух слагаемых: внешнего избыточного давления на свободной поверхности и весового давления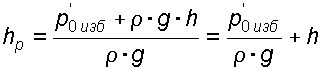

                                                                             (2.24)

Избыточное давление может быть и отрицательной величиной, называемой вакуумом. Так, во всасывающих патрубках центробежных насосов, в потоке жидкости при истечении из цилиндрических насадков, в вакуум – котлах в жидкости образуются области с давлением ниже атмосферного, т.е. области вакуума.

В этом случае:

                                                                                                                (2.25)

                                                                                                    (2.26)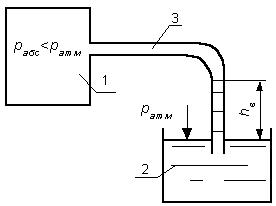

                                                               (2.27)

 

    Рис.2.5. Ваккумметрическая высота

Вакуум – это недостаток давления до атмосферного.

Пусть в резервуаре 1 (рис. 2.5) абсолютное давление меньше атмосферного (например, откачана часть воздуха при помощи вакуум-насоса). В резервуаре 2 находится жидкость, и резервуары соединены изогнутой трубкой 3. На поверхности жидкости в резервуаре 2 действует атмосферное давление.

Так как в резервуаре 1 давление меньше атмосферного то жидкость поднимается в трубке 3 на какую-то высоту, которая называется вакуумметрической высотой и обозначается.Величина может быть определена из условия равновесия:

                                                                                         (2.28)

                                                                                                     (2.29)

Максимальное значение вакуумметрического давления составляет 98,1кПа или 10 м.в.ст., но практически давление в жидкости не может быть меньше давления паров насыщения и равно 7–8 м.в.ст.

 

2.1.6. Условия равновесия жидкости в сообщающихся сосудах

Рассмотрим два сообщающихся сосуда, наполненных различными, не смачивающимися между собой жидкостями (рис. 2.6).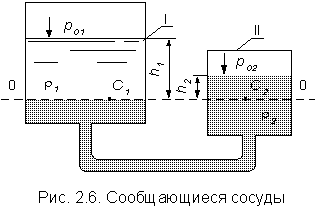

    Сосуды закрыты, давления и – на поверхности жидкостей в сосудах I и II различны. Линия О-О – линия раздела разнородных жидкостей. Горизонтальная плоскость, проходящая через линию О-О, является плоскостью равного давления. Определим величину гидростатического давления в точках и , лежащих на плоскости равного давления. Согласно основному уравнению гидростатики:

                                                                                              (2.30)

                                                                                         (2.31)

где и – возвышение поверхности жидкостей в сосудах I и II над плоскостью О-О; и – плотности жидкостей.

Очевидно, что:

                                                                         (2.32)

                                                                         (2.33)

Зависимость (2.33) характеризует условия равновесия жидкостей в сообщающихся сосудах. Она позволяет решать частные задачи.