Гидравлика. Лекция по гидравлики. Гидравлика представляет собой теоретическую дисциплину, изучающую вопросы
 Скачать 1.29 Mb.
|
|
11.2. Основные методы гидравлического расчёта безнапорных потоков Равномерное движение жидкости в безнапорном потоке поддерживается за счёт разницы в уровне свободной поверхности между начальным и конечным живыми сечениями потока. Чтобы движение жидкости в потоке было равномерным, должны быть выполнены следующие необходимые условия: живые сечения потока вдоль всего русла должны быть одинаковыми как по размеру, так и по форме, уровень свободной поверхности жидкости должен быть параллелен профилю дна русла, шероховатость стенок русла должна быть одинакова по всей длине русла. При выполнении этих условий гидравлический расчёт сводится в основном к определению расхода в потоке жидкости, а также некоторых параметров потока. Выделим в потоке жидкости двумя живыми сечениями (1-1 и 2 - 2) отсек потока длиной /. Центры тяжести сечений будут находиться соответственно на уровнях и от произвольно выбранной плоскости сравне 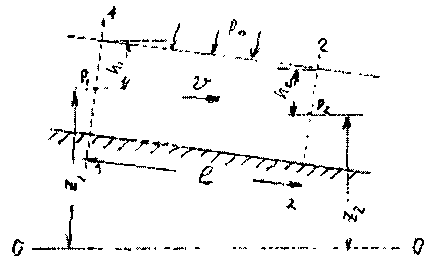 ния О -О и на глубинах соответственно и под уровнем свободной поверхности жидкости. Тогда запишем уравнение Бернулли для этих двух сечений потока. Поскольку по условиям равномерности потока и , то уравнение Бернулли примет вид: t ? где: - потери напора по длине отсека потока /. Согласно известному уравнению Шези средняя скорость в живом сечении потока: Величина скоростного коэффициента Шези С определяется по экспериментальной формуле Маннинга: где: п - величина шероховатости стенок русла. Или по формуле Павловского: где: при при 11.3. Движение жидкости в безнапорных (самотёчных) трубопроводах Безнапорные самотёчные трубопроводы прокладываются, как правило, в заглублённом исполнении. Для строительства таких трубопроводов помимо труб круглого сечения (1) часто используются трубы овоидального (2) и лоткового (3) сечений. При гидравлическом расчёте безнапорных трубопроводов независимо от вида их сечения при 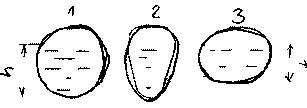 ходится решать задачи трёх основных типов:определение расхода жидкости, пропускаемого данным трубопроводом, определение уклона дна, необходимого для пропуска заданного расхода жидкости при заданном заполнении сечения, определение степени наполнения трубопровода для пропуска заданного расхода жидкости при известном уклоне дна. Решение всех этих задач сводится к решению уравнения Шези при различных вариантах задания исходных данных Анализируя результаты решения таких задач нетрудно обнаружить, что для каждого сечения трубопровода существует так называемая эффективная степень заполнения русла, при которой достигается максимальный расход при условии минимальо возможных потерях напора Это объясняется тем, что при увеличении площади живого сечения потока увеличивается также и длина смоченного периметра Начиная с некоторой величины (соответствующей эффективной степени заполнения русла), увеличение длины смоченного периметра начинает «обгонять» рост площади живого сечения. При этом дальнейшее увеличение расхода жидкости в трубопроводе будет сопряжено со значительными потерями напора. 12. Движение неньютоновских жидкостей 12.1. Некоторые характеристики и реограммы неньютоновских жидкостей. Изучение процесса движения неньютоновских жидкостей является весьма трудоёмкой задачеё как с точки зрения полноты понимания всех физико-химических процессов сопровождающих такое движение сложного физического тела, так и с точки зрения математического описания этого явления. Как известно, все неньютоновские жидкости отличаются от классической ньютоновской жидкости видом зависимости градиента давления от величины касательного напряжения. Графики таких зависимостей носят на- звание кривых течения неньютоновских жидкостей или реограмм. На рисунке представлены реограммы различных типов неньютоновских жидкостей (1 - дилатантная жидкость, 3 - псевдопластическая жидкость, 4 - вязкопластическая жидкость) по сравнению с аналогичной характеристикой классической ньютоновской жидкостью (линейная зависимость - 2). Первые два вида неньютоновских жидкостей: дилатантные и псевдопластические описываются одинаковыми уравнениями реограмм с различными характеристиками коэффициентов k -меры консистенции жидкости и п - меры степени отличия поведения неньютоновской жидкости от классической ньютоновской жидкости. 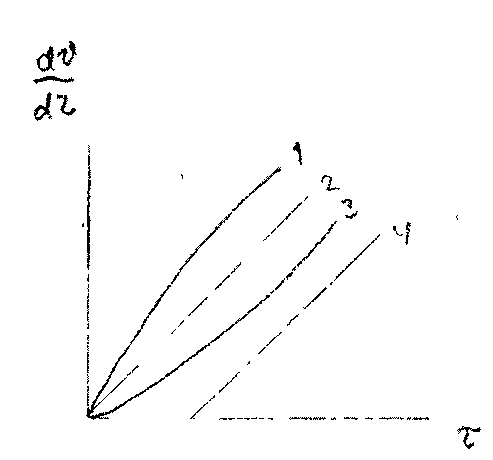 Для характеристики названных выше типов неньютоновских жидкостей часто используется ещё одна дополнительная мера - эффективная кажущаяся вязкость жидкости. Суть этой меры состоит в том, что для любой конкретной величины касательного напряжения в неньютоновской жидкости можно поставить в соответствии величину вязкости ньютоновской жидкости с одинаковой величиной касательных напряжений, т.е. реограмма реальной неньютоновской жидкости заменяется линейной зависимостью:Естественно, что величина эффективной кажущейся вязкости жидкости будет зависеть от интервала значений касательного напряжения, на котором эта величина вычисляется. Вязкопластические (бингамовские) жидкости обладают как свойствами твёрдого тела (при напряжениях меньших величины статического напряжения сдвига ), так и свойствами жидкости (при касательных напряжениях в жидкости ). Когда вязкопла- стическая жидкость проявляет свойства твёрдого пластичного тела, то роль кристаллической решётки в вязкопластической жидкости осуществляет образующаяся в ней жёсткая 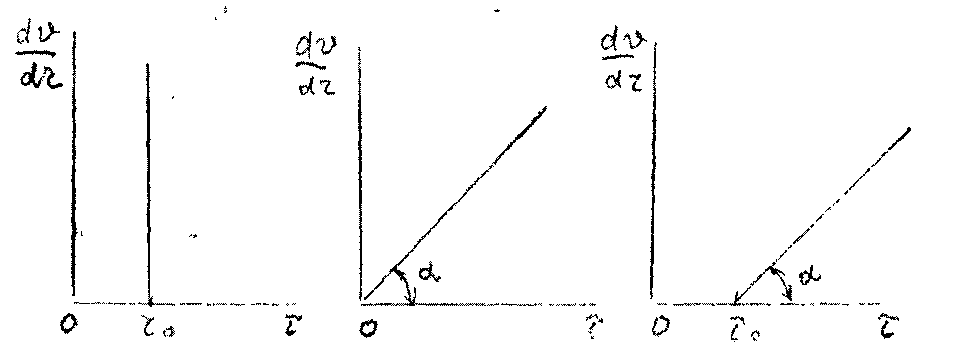 пространственная структура, приводящая к полной неподвижности жидкости. Поэтому реограмму вязкопластических жидкостей (в) принято рассматривать как некоторую сумму реограмм твёрдого пластичного тела (а) и классической ньютоновской жидкости (б). Уравнение такой реограммы можно представить в следующем виде: Вид реограмм неньютоновских жидкостей, в том числе и вязкопластичных жидкостей, осложняется проявлением тиксотропных свойств таких жидкостей. Принято считать, что величина статического напряжения сдвига вязкопластичных жидкостей зависит от продолжитнльности нахождения такой жидкости в состоянии покоя, другими словами, прочность образующейся структурной решётки в вязкопластичной жидкости увеличивается со временем. Повторное приведение жидкости в состояние движения происходит при значительно более низком статическом напряжении сдвига. Поэтому принято различать величину начального статического напряжения сдвига (после длительной остановки жидкости) и динамическую величину (после кратковременных перерывов в работе). Тиксо-тропные свойства жидкостей обратимы, т.е. при восстановлении существовавшего ранее режима течения жидкости их действие прекращается. Следует также отметить тот факт, что на величину статического напряжения сдвига в значительной степени влияет вибрация, разрушающая образующуюся в жидкости пространственную структуру. При этом величина т0 может быть снижена практически до 0, и поведение такой жидкости не будет отличаться от классической ньютоновской жидкости. Особенности строения вязкопластических жидкостей приводят к некоторым парадоксам. Так, к примеру, в сообщающихся сосудах с вязкопластической жидкостью уровни в коленах сосудов устанаыливаются на разных высотах, зависящих от свойств жидкости и у размеров сосудов. ! * 12.2. Движение вязкопластических жидкостей в трубах. Для того, чтобы вязкопластичная жидкость начала перемещаться необходимо создать между начальным и конечным сечениями участка трубы длиной / некотурую разность напоров, при которой будет преодолена величина начального статического напряжения сдвига . При этом жидкость отрывается от стенок трубы и первоначально движется на подвижном ламинарном слое, сохраняя свою прежнюю пространственную структуру, т.е. с одинаковыми скоростями по всему отсеку потока. Разрушение этой структуры происходит позже и при некотором превышении напора. Поскольку в начальный момент времени силы трения будут возникать только у стенок трубы, то уравнения равновесия можно запмсать в следующем виде: 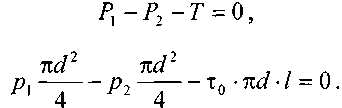 Необходимая разность напоров между началом и концом участка трубы определится следующим образом: Таким образом, при превышении разности напоров расчётную величину жидкость начнёт двигаться по трубе, причём характер (режим) её движения будет зависеть от величины . При движении вязкопластичной жидкости возможны три режима течения её: структурный, ламинарный и тутбулентный. Условие является необходимым для начала движения жидкости в структурном режиме, при этом под величиной статического напряжения сдвига следует понимать величину соответствующую длительному покою жидкости, т.е. с учётом проявления тиксотропных свойств жидкости. Структурный режим течения жидкости предполагает наличие вдоль стенок трубы сплошного ламинарного слоя жидкости; в центральной части трубы наблюдается ядро те- чения, где жидкость движется, сохраняя прежнюю свою структуру, т.е. как твёрдое тело. Размеры центрального ядра течения (радиус ) может быть определён исходя из следующего соотношения: При увеличении А/г размеры ламинарной зоны будут постепенно увеличиваться за счёт уменьшения размеров ядра течения пока структурный режим не перейдёт в полностью ламинарный режим движения жидкости. В дальнейшем ламинарный режим постепенно сменится турбулентным режимом движения жидкости. Для определения закона распределения скоростей по сечению потока при структурном режиме движения жидкости запишем некоторую функцию для касательных напряжений в соответствии с 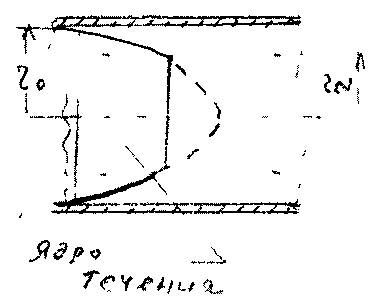 формулой Бингама:Тогда распределение скоростей по сечению трубы можно выразить следующим образом:  ?где: - касательное напряжение на стенке трубы радиуса , - скорость жидкости на расстоянии от центра трубы. После интегрирования этого уравнения получим: 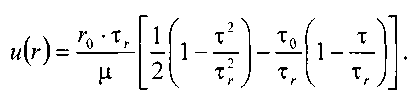 И окончательно:  Для определения скорости в ядре течения примем , где - радиус ядра течения (структурной части потока жидкости). Тогда величина скорости в этом ядре течения (скорости в ядре течения одинаковые равны) : '  Расход жидкости при структурном движении можно определить, используя известные соотношения дл круглой трубы:  Интегрируя уравнение в пределах от до , получим: 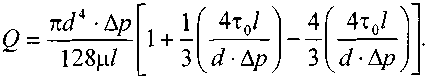 5 f Последнее уравнение, известное как формула Букингама, можно упростить: 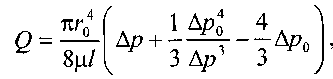 где: - разность давлений при начале движения жидкости, когда каса- тельнве напряжения в ней достигают величины касательного напряжения сдвига. Если пренебречь величиной второго члена ввиду его малости, получим:    * где: - обобщённый критерий Рейнольдса.Комплексный параметр = Sen носит название числа Сен-Венана. Таким образом, при расчётах движения вязкопластических жидкостей можно пользоваться уравнениями для ньютоновских жидкостей, заменяя в уравнениях величину числа Рейнольдса Re на обобщённый критерий Рейнольдса Турбулентный режим течения жидкости. Характер течения вязкопластических жидкостей существенно не отличается от турбулентного потока ньютоновских жидкостей. Отличие состоит в количественных соотношениях между величинами коэффициентов трения и числом Рейнольдса. Так коэффициент трения может быть выражен как функция обобщённого числа Рейнольдса (в общем виде) следующим образом: где: В и п - некоторые параметры, устанавливаемые по данным экспериментов. Так по данным экспериментов Б.С. Филатова величины коэффициентов В и п принимаются следующими: - для неутяжелённого глинистого раствора В = 0,1 и п = 0,15, - для утяжелённого глинистого раствора В = 0,0025 и п = -0,2. Для расчёта трубопроводов при ждижении по ним глинистых и цементных растворов можно пользоваться формулой Б.И. Мительмана: при: Re* =2500-40000. 12.3. Движение вязкопластичных жидкостей в открытых каналах В практике работы горных предприятий не редки случаи, когда приходится транспортировать неньютоновские жидкости в безнапорных потоках (самотёком), в лотках, по желобным системам. Характер течения вязкопластичных жидкостей в открытых каналах при структурном режиме идентичен аналогичному и напорному потокам такой жидкости в круглых трубах. Т.е. при структурном режиме течения жидкости также выделяется центральное ядро течения, где жидкость движется как твёрдое тело, сохраняя свою первонв-чальную структуру. Ядро течения подстилается непрерывным ламинарным слоем жидкости. Течению таких жидкостей по открытым каналам прямоугольного профиля посвящены работы Р.И. Шищенко. По данным его исследований расход вязкопластичной жидкости при структурном режиме движения может быть определён по приближённой формуле: 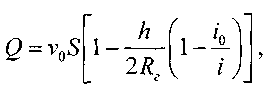 где: - скорость течения ядра потока  - площадь живого сечения канала шириной bи глубиной заполнения h, - гидравлический уклон, соответствующий началу течения жидкости, / - уклон дна канала, - гидравлический радиус живого сечения потока. 12.4. Движение неньютоновских жидкостей, подчиняющихся степенному реологическому закону, по трубам Для жидкостей, подчиняющихся степенному реологическому закону, функция напряжения сдвига будет иметь следующий вид: Тогда распределение скоростей в сечение потока будет соответствовать следующей зависимости: 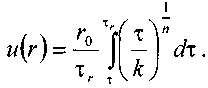 Интегрируя это уравнение, найдём:  , или:Отсюда можно получить выражение для расхода жидкости: 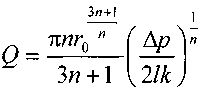 Отсюда определим величину перепада давления, обеспечивающую движение жидкости и соответствующую величину потерь напора на трение. 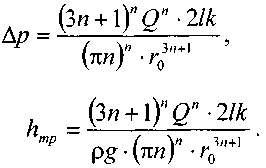 Сопоставляя полученное выражение с формулой Дарси-Вейсбаха, найдём величину коэффициента трения и обобщённый критерий Рейнольдса: 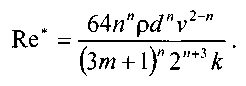  13. Гидравлическая теория смазки 13.1. Ламинарное движение жидкости в узких щелях В большинстве машин и механизмов с целью снижения трения между движущимися узлами используются принципы гидравлической смазки, когда малые зазоры между соприкасающимися элементами заполняются низковязкой или другой жидкостью. В данном случае процесс сухого трения между твердыми движущимися телами заменяется скольжением. Гидравлическая смазка используется также и в случаях, когда необходимо выполнить изоляцию зазоров от проникновения через них жидкостей. Эти чисто практические задачи связаны с теорией течения жидкости в узких щелях, разработанных Буссинэ и Н.П. Петровым. Эту задачу рассмотрим на классическом уровне. Возьмём две плоские одинаковые 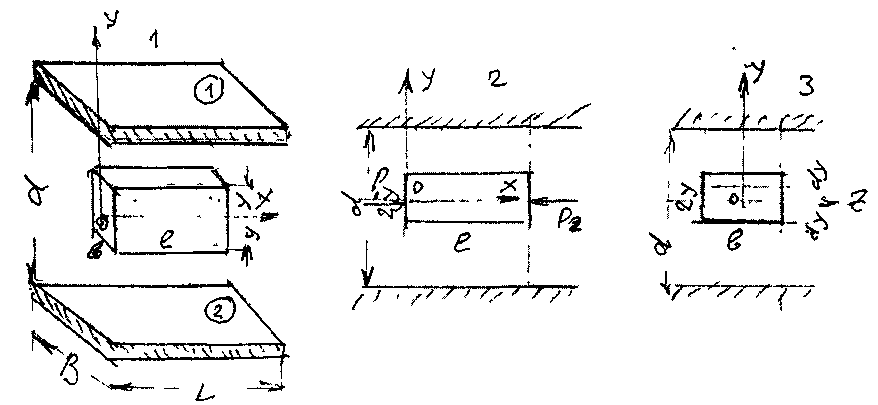 пластины, расположенные параллельно друг другу на малом расстоянии друг от друга. Эти пластины образуют межды собой тонкую щель (зазор) d. Щель будет считаться тонкой, если её ширина dво много раз меньше размеров пластин и , где Lи В - размеры пластины. Проведем в потоке щели два параллельных друг другу сечения на расстоянии / и выделим малый отсек жидкости в виде параллелепипеда со сторонами: и 2у. Жидкость движется вдоль оси ОХ (на рисунке 2 слева на право). Грани, через которые жидкость втекает внутрь выделенного отсека и вытекает из него, имеют площадь . К этим граням приложены силы давления равные: Гогда выделенный отсек жидкости будет находиться в состоянии равновесия под действием сил давления трения и силы тяжести. 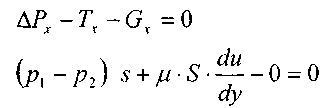 где: - площадь верхней и нижней граней отсека жидкости. Подставив в уравнение величины площади пластин и граней, и преобразовав уравнение, получим:  Тогда: 5 где: - гидравлический уклон. |