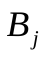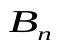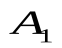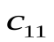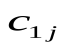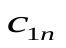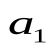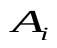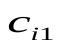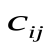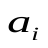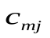ГОСы. Государственное регулирование предпринимательской деятельности
 Скачать 387.97 Kb. Скачать 387.97 Kb.
|
|
Современные методы проведения экспертизы для решения профессиональных задач с помощью метода «Дельфи». Метод «Дельфи» - метод быстрого поиска решений, основанный на их генерации в процессе «мозгового штурма», проводимого группой специалистов, и отбора лучшего решения, исходя из экспертных оценок. Дельфийский метод используется для экспертного прогнозирования путем организации системы сбора и математической обработки экспертных оценок. Базовым принципом метода является то, что некоторое количество независимых экспертов (часто несвязанных и не знающих друг о друге) лучше оценивает и предсказывает результат, чем структурированная группа (коллектив) личностей. Позволяет избежать открытых столкновений между носителями противоположенных позиций, так как исключает непосредственный контакт экспертов между собой. Субъекты: группы исследователей, каждый из которых отвечает индивидуально в письменной форме; организационная группа – сводит мнения экспертов воедино. План действий: Сформировать рабочую группу для сбора и обобщения мнений экспертов. Сформировать экспертную группу из специалистов, владеющих вопросами по обсуждаемой теме. Подготовить анкету, указав в ней поставленную проблему, уточняющие вопросы. Формулировки должны быть четкими и однозначно трактуемыми, предполагать однозначные ответы. Провести опрос экспертов в соответствии с методикой, предполагающей при необходимости повторение процедуры. Полученные ответы служат основой для формулирования вопросов для следующего этапа. Обобщить экспертные заключения и выдать рекомендации по поставленной проблеме. Каковы критерии выбора пакетов прикладных программ, необходимых для реализации вычислений в соответствии с построенными экономико-математическими моделями? Экономико-математические модели – это модели экономических объектов или процессов, при описании которых используются математические средства. В практическом плане экономико-математические модели используются как инструмент прогноза, планирования, управления и совершенствования различных сторон экономической деятельности общества. Экономико-математические модели отражают наиболее существенные свойства реального объекта или процесса с помощью системы уравнений. Единой классификации экономико-математических моделей не существует, хотя можно выделить наиболее значимые их группы в зависимости от признака классификации. По целевому назначению модели делятся на: Теоретико-аналитические (используются в исследовании общих свойств и закономерностей экономических процессов); Прикладные (применяются в решении конкретных экономических задач, таких как задачи экономического анализа, прогнозирования, управления). По учету фактора времени модели подразделяются на: Динамические (описывают экономическую систему в развитии); Статистические (экономическая система описана в статистике, применительно к одному определенному моменту времени; это как бы снимок, срез, фрагмент динамической системы в какой-то момент времени). По длительности рассматриваемого периода времени различают модели: Краткосрочного прогнозирования или планирования (до года); Среднесрочного прогнозирования или планирования (до 5 лет); Долгосрочного прогнозирования или планирования (более 5 лет). По цели создания и применения различают модели: Балансовые; Эконометрические; Оптимизационные; Сетевые; Систем массового обслуживания; Имитационные (экспертные). На современном весьма конкурентном рынке программных средств несомненное лидерство занимает пакет, объединивший в одном названии целое семейство продуктов фирмы Microsoft — MicrosoftOffice (MS Office). Пакет MicrosoftOffice объединяет несколько программ, основными из которых являются: текстовый процессор MS Word, который используется для создания текстовых документов (писем, отчетов, книг и т.д.); система электронных таблиц MS Excel, которая позволяет проводить числовой анализ и представлять данные в наглядной форме; система управления базами данных MS Access. В настоящее время существуют такие мощные компьютерные пакеты, как MathCAD, Mathematica, Mathlab, Maple, Derive, Theorist и т. д. Примеры экономико-математических моделей: Задача об использовании ресурсов (задача планирования производства). При производстве Решение. Обозначим 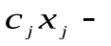 прибыль от реализации всего объема прибыль от реализации всего объема 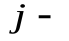 й продукции, й продукции, 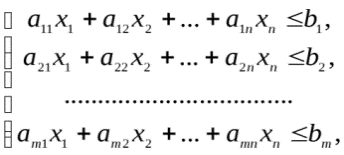 Транспортная задача. Однородный груз сосредоточен у 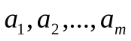 . Данный груз необходимо доставить . Данный груз необходимо доставить 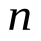 потребителям потребителям 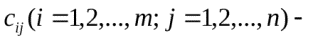 стоимость перевозки единицы груза от каждого стоимость перевозки единицы груза от каждого мощности всех поставщиков были реализованы; спросы всех потребителей были удовлетворены; суммарные затраты на перевозку были минимальны. Исходные данные транспортной задачи записываются в виде таблицы
Решение. Обозначим  объемы перевозок от каждого объемы перевозок от каждого  при условиях при условиях 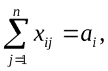 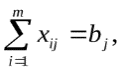 Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.  , то модель такой транспортной задачи называется закрытой. Для решения задач линейного программирования в программе MicrosoftExcel имеется надстройка Поиск решения, обращение к которой производится из меню Сервис. , то модель такой транспортной задачи называется закрытой. Для решения задач линейного программирования в программе MicrosoftExcel имеется надстройка Поиск решения, обращение к которой производится из меню Сервис.Каковы особенности выбора необходимого пакета прикладных программ для реализации вычислений параметров производственных функций различных типов? Производственная функция (ПФ) – это зависимость объема выпуска продукции у от используемого или затрачиваемого ресурсах (фактора производства) у = f(x). Здесь х (х ≥ 0) и у (у ≥ 0) – числовые величины т.е. у = f(x) есть функция одной переменной х. В связи с этим, ПФ f(x) называется одноресурсной или однофакторной ПФ. Показатели, в которых измеряются переменные, могут быть различными: стоимостными, натуральными, безразмерными. В микроэкономической теории принято считать, что у– это максимально возможный объем выпуска продукции, если ресурс затрачивается в количестве х единиц. В макроэкономике такое понимание не совсем корректно: возможно при другом распределении ресурсов между структурными единицами экономической системы выпуск мог бы быть и больше. Поэтому более правильной является запись однофакторной ПФ в форме: у = f(x,а), где а– вектор параметров структуры системы. Существуют следующие модели: Линейная модель, Квадратичная модель, Модель Кубба-Догласа,Модель с учетом НТП Метод наименьших квадратов (МНК) применяется для построения регрессионных моделей при обработке экспериментальных данных. Используя исходные данные и модель производственной функции( 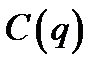 . Используя систему EXEL, найдем по данной системе неизвестные параметры. . Используя систему EXEL, найдем по данной системе неизвестные параметры.В системе MathCad построим поверхность | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||