финалочка моя. Характеристика инфраструктурных отраслей региона. 3
 Скачать 1.08 Mb.
|
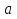 для данного регрессионного уравнения меньше 1, следовательно, временной ряд является стационарным.Таблица 2.34 – Исходные данные для теста Дики-Фуллера (Х7)
Таблица 2.35 – Исходные данные для теста Дики-Фуллера (Х7) 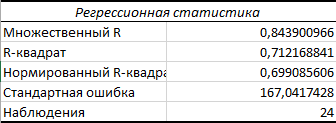 Таблица 2.36– Исходные данные для теста Дики-Фуллера (Х7)  Таблица 2.37 - Регрессионная статистика (Х7)
Коэффициент 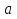для данного регрессионного уравнения меньше 1, следовательно, временной ряд является стационарным.Согласно результатам теста Дики-Фуллера, все временные ряды, кроме Х3, являются стационарными. Показатель (Х3) дальше в исследовании не участвует. 5. Проверить экзогенные параметры на мультиколлинеарность. В случае если коэффициент попарной корреляции превышает 0,7, следует исключить из дальнейшего анализа одну переменную из пары. Таблица 2.38 – Коэффициенты корреляции 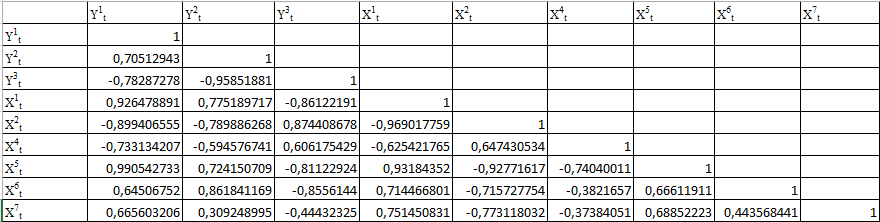 Показатели Х1 и X5 имеют тесную связь, но из исследование они не будут исключены, так как по результатам теста Дикки-Фулера уже был исключен один экзогенный показатель. X1 и X7 так же имеют тесную связь и они буду удалены из исследования. Также из таблицы видно, что эндогенные показатели имеют между собой тесную связь, что говорит о взаимовлиянии. 6. Осуществим проверку коэффициентов парной корреляции на значимость с помощью t-критерия Стьюдента для показателей. Если tрасч≥tтабл, то полученные коэффициенты значимы т.е. выборка соответствует генеральной совокупности (Таблица ). Для оценки значимости коэффициентов корреляции следует рассчитать t-критерий Стьюдента для каждой попарной корреляции по формуле: 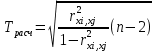 (6)Таблица 2.3.39 – Значения t-критерия Стьюдента для показателей 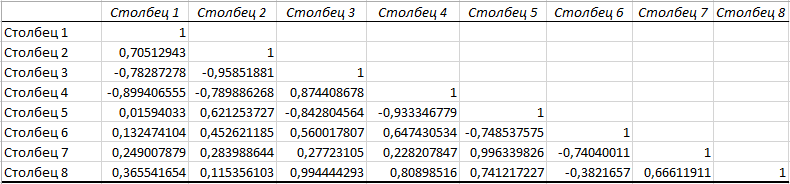 При уровне значимости α=0,05, числу степеней свободы n-2=18, tтабл=2,1. Так как tрасч>tтабл, коэффициенты считаются значимыми. 7. Проверим автокорреляцию показателей, а именно определим лаги, имеющие сильную корреляционную связь со значением показателя в последнем периоде. Далее проверим значимость коэффициентов автокорреляции с помощью Ljung-Box Q-test Проверка значимости коэффициентов автокорреляции по Q-статистике Льюнга-Бокса осуществляется по формуле: 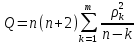 (7)где n - число наблюдений, ρk - автокорреляция k-го порядка, и m - число проверяемых лагов. В случае если 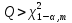 , коэффициенты считаются значимыми.  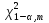определяется по таблице.Таблица 2.40 - Коэффициенты автокорреляции переменной (Y1)
Так как более точной является Q-статистика Льюнга-Бокса, для анализа она является более предпочтительной. Анализ автокорреляции в программе Statistica помимо коэффициентов автокорреляции автоматически рассчитывает Q-статистику Льюнга-Бокса и значимость для каждого коэффициента. Проверка значимости по Q-статистике Льюнга-Бокса равна |