Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 76 из 101

нагрузка Q’_T, ГДнс/с

Рис. 13.3. Зависимость полной экономии расчетных затрат от присоединенной тепловой нагрузки

марная мощность отборов турбин и пико­вых котельных.

Удельная мощность ТЭЦ — весьма удобный показатель для предварительной оценки целесообразного значения электри­ческой мощности ТЭЦ для вновь проекти­руемых районов централизованного тепло­снабжения, а также при развитии действую­щих теплофикационных систем:

^опт = <^ПХ (13.86а)

Во втором случае, когда заданы ус­тановленная мощность ТЭЦ N и тепловая мощность отборов турбин £?'_отб, определе­ние а _т заключается в расчете оптимальной тепловой нагрузки (?'_пт, при которой абсо­лютная экономия расчетных затрат при теп­лофикации по сравнению с раздельным энергоснабжением максимальна, т.е. ДЗ = = Дз£?' = шах.

Для этой цели на основе удельной эконо­мической характеристики турбин Дз =/(2т) (рис. 13.3) строится интегральная характе­ристика ДЗ = Дз£?', т.е. зависимость полной экономии расчетных затрат ДЗ от расчетной тепловой нагрузки ТЭЦ Q'_T .Точка перегиба кривой И АЗ = f (Q'_t) соответствует опти­мальному значению Q'_T для рассматривае­мой задачи.

Для иллюстрации на рис. 13.3 приведена зависимость ДЗ = f (Q'_T) для ТЭЦ с одним теплофикационным блоком Т-250-240 (кри­вая Г). Точка перегиба кривой / определяет значения ^_опт. Коэффициент теплофика­ции, соответствующий этой нагрузке, а°^пт = 0,43. Из сравнения характеристик, приведенных на рис. 13.2 и 13.3, видно, что оптимальное значение коэффициента теп­лофикации, выбранное из условия макси­мальной полной экономии расчетных за­трат ДЗ = шах, в 0,66/0,43 = 1,5 раза ниже оптимального коэффициента теплофика­ции, выбранного из условия максимальной удельной экономии расчетных затрат.

Такая закономерность, характерная для современных ТЭЦ, показывает, что при вто­рой формулировке задачи, т.е. когда физи­чески установленная электрическая мощ­ность данной ТЭЦ ограничена и не может быть увеличена из-за отсутствия свободной площадки или по другим условиям, опти­мальное значение тепловой нагрузки на один агрегат выше, а оптимальный коэф­фициент теплофикации а °^пт ниже, чем при первой формулировке задачи, когда число устанавливаемых агрегатов на ТЭЦ не огра­ничено. Это объясняется тем, что при увели­чении присоединенной тепловой нагрузки на агрегат сверх значения, соответствующе­го экстремуму кривой Дз = f (Q'_T), наряду с уменьшением удельной экономии приве­денных затрат растет отпуск теплоты от ТЭЦ, в том числе и из отборов турбин; по­этому полная экономия приведенных затрат в некотором диапазоне значений Q'^ возрас­тает. Конечно, при этом полная экономия приведенных затрат получается меньше, чем при варианте установки дополнитель­ных турбоустановок с ростом присоединен­ной к ТЭЦ тепловой нагрузки.

Из рис. 13.3 видно, что при установке на ТЭЦ только одного блока Т-250-240 и огра­ничении присоединенной к нему тепловой нагрузки £?'_т1, соответствующей а°^пт по первой формулировке задачи, полная эко­номия расчетных затрат составляет Д3[. Ес­ли же увеличить тепловую нагрузку, при­соединенную к этому блоку, до (?'_гопт, то полная экономия расчетных затрат возрас­тает до Д3₂.

На рис. 13.3 нанесена кривая II, показы­вающая полную экономию расчетных за­трат ДЗ, которая могла бы быть получена, если бы при тепловой нагрузке (?т_опт вве­ли бы в работу второй теплофикационный блок Т-250-240. Из сравнения характери­стик I н II видно, что при расчетной тепло­вой нагрузке £?'_топт, являющейся опти­мальной из условия ДЗ = max для ТЭЦ с од­ной турбиной Т-250-240, полная годовая экономия расчетных затрат равна Д3₂, в то время как при установке двух турбин Т-250-240 она равна Д3₃, т.е. больше, чем в первом случае.

По найденной оптимальной тепловой нагрузке ТЭЦ £?'_топт, соответствующей ДЗ_тах, при второй формулировке задачи легко определить оптимальную удельную тепловую нагрузку ТЭЦ, отнесенную к еди­нице установленной электрической мощно­сти ТЭЦ:

«опт ₌ q,

Величина представляет собой

удобный показатель для предварительного вычисления целесообразной расчетной теп­ловой нагрузки ТЭЦ при заданной установ­ленной электрической мощности.

Определение оптимальной расчетной температуры воды. Значение оптималь­ной расчетной температуры воды в подаю­щем трубопроводе водяной тепловой сети зависит от трех звеньев теплофикационной системы: ТЭЦ, тепловой сети, теплоисполь­зующих установок. Когда теплота поступа­ет от котельной, работающей в составе сис­темы централизованного теплоснабжения, повышение температуры в подающем тру­бопроводе до технически допустимого пре­дела всегда выгодно. При теплоснабжении от ТЭЦ задача решается сравнением вари­антов теплоснабжения с различной темпе­ратурой воды в подающем трубопроводе, при этом оптимальной температуре воды соответствуют минимальные расчетные за­траты

3. 
   = ^_ТОп ⁺ ^п ⁺ ^т.п ⁺ (Л.с ⁺ ^т.с ⁺
   

+ (Лб ^{+ = min}> (13.87)

где /_тс, /_а — доли отчислений от капиталь­ных затрат соответственно в тепловые сети и насосные станции, учитывающие посто­янные издержки. Обозначения И_топ, И_п, И_тп — см. (13.29), (13.63), (13.69).

При определении зависимых расходов необходимо для каждого из сравниваемых вариантов выбрать свое экономическое удельное падение давления Л°^пт, посколь­ку оно зависит от расчетного расхода воды в сети, а расчетный расход воды будет раз­личным для разных вариантов, так как G =/(Дт').

При теплоснабжении жилых и общест­венных зданий максимальная температура воды, поступающей в отопительные систе­мы, ограничена по санитарно-гигиениче­ским условиям 90—95 °C. Поэтому повы­шение температуры воды в подающем трубопроводе не отражается на поверхно­сти нагрева приборов абонентских отопи­тельных установок.

13.8. ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО
УДЕЛЬНОГО ПАДЕНИЯ ДАВЛЕНИЯ В СЕТИ

Современные двухтрубные магистраль­ные водяные тепловые сети представляют собой обычно сложную циркуляционную систему с основной насосной установкой на ТЭЦ и насосными подстанциями на по­дающем и обратном трубопроводах и мно­гочисленными ответвлениями от магистра­

лей, по которым сетевая вода проходит из подающего в обратный трубопровод через теплопотребляющне установки. Принци­пиальная схеме такой тепловой сети и ее пьезометрический график приведены на рис. 13.4.

Оптимальное удельное линейное паде­ние давления в магистральной тепловой се­ти зависит от годовых расчетных затрат по тепловой сети, включающих стоимость тепловых потерь.

Увеличение удельного линейного паде­ния давления приводит к уменьшению диа­метров сети и связанному с этим ее удешев­лению, но при этом возрастают затраты на сооружение насосных станций, увеличива­ется расход электроэнергии и соответствен­но годовые издержки на перекачку теплоно­сителя.

Экономическое решение задачи соответ­ствует минимуму суммы расчетных затрат

3 = //_{п +} //_{тп +} (/_{н +} £)К_н +

+ (/_TC + £)K_TC = min, (13.88)

где/_н, _с — доля ежегодных отчислений от капитальных затрат соответственно в на­сосные станции и тепловые сети, учиты­вающие постоянные издержки насосных станций и тепловых сетей; К_к — капи­тальные затраты в насосные станции; К_1й —

^хи2 ^хпЗ



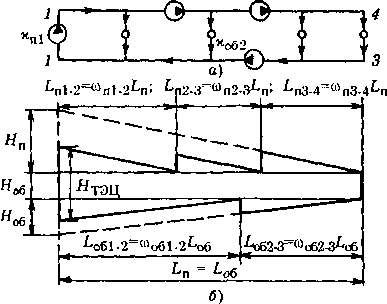
Рис. 13.4. Принципиальная схема тепловой сети (в) и ее пьезометрический график (б)

то же в тепловые сети. Остальные буквен­ные обозначения — см. формулы (13.68), (13.69), (13.16), (13.63).

Капитальные затраты в насосные стан­ции, руб.,

= ⁺ (13.89)

где — постоянная составляющая капи­тальных затрат в насосную станцию; с_н — суммарное количество насосных станций и подстанций на ТЭЦ и магистральной теп­ловой сети; Ь_н — удельные капитальные затраты в насосную станцию, зависящие от ее установленной мощности, руб/кВт; 2У₍₁ — суммарная электрическая мощность насосных станций, требуемая для перекач­ки теплоносителя по магистральной тепло­вой сети, кВт,
Здесь G — суммарный расчетный расход воды в сети (подача с коллектора ТЭЦ), кг/с; Л., — удельное линейное падение дав­ления в главной магистрали, Па/м; L — сум­марная длина главной магистрали (сумма длин подающего и обратного трубо­проводов), м; а — коэффициент местных гидравлических потерь; г|_{н у} — КПД насос­ной установки; х — коэффициент расхода насосной станции (подстанции), равный от­ношению сетевого расхода воды через на­сосную станцию к суммарному расчетному расходу воды в сети, т.е. к подаче воды с коллекторов ТЭЦ, х = G_H/G; G_H — расход воды через насосную станцию; со — дистан­ционный коэффициент насосной станции или подстанции, равный отношению рас­стояния между двумя последовательно включенными станциями и от последней по ходу воды станции до конца магистрали к длине магистрали, на которой они уста­новлены, т.е. к длине подающего или к дли­не обратного трубопровода (например, из рис. 13.4 co_ri2.₃ = L_nl,ylL_n, где Л_гг2.₃ — рас­стояние между подстанциями № 2 и 3 на по­дающем трубопроводе; L_n — длина подаю­щего трубопровода магистрали). Насосной станции на ТЭЦ присвоен № 1. Как по по­дающему, так и по обратному трубопро­водам нумерация насосных начинается с ТЭЦ, т.е. от насосной станции № 1.

При указанной системе нумерации на­сосных станций имеют место следующие зависимости:

“nl-2 ⁺ “п2-3 ⁺- ⁺ “п[(и- 1)- п] ⁼ к

“об 1-2 ⁺ “об2-3 ⁺- ⁺ “об[(л- 1)-л] ⁼ Ь где со_п — дистанционные коэффициенты подающей магистрали; со_об — дистанцион­ные коэффициенты обратной магистрали.

Сумма произведений коэффициентов расхода на дистанционные коэффициенты насосных станций на подающем и обратном трубопроводах магистралей равна

2х(о = х_п1(о_п1.₂ + х_п2(о_п2.₃ + ...

••• ^{+ x}o6l“o61-2 ^{+ х}об2^юоб2-3'

Комплекс Zxco/2 в (13.90) — это коэф­фициент снижения мощности на перекачку теплоносителя ио магистральной сети при работе насосных подстанций.

В частном случае, при равномерном рас­пределении тепловой нагрузки вдоль магист­рали и равномерном распределении насос­ных станций на магистрали (сю,,^ = ^ю_п2-3 - = ^Ю0б 1-2 ⁼ “об2-з) величина £хсо/2 = (с_н + + 3)/(2с_н + 2), где с_н — количество насосных станций.

При отсутствии насосных подстанций, т.е. при наличии только одной насосной станции на ТЭЦ, с_н = 1 и Ехсо/2 = 1. При уве­личении числа насосных станций значение Ехоэ/2 уменьшается. Так, при установке в середине подающей и обратной магистра­ли по одной подстанции с = 3 и Zxco/2 = = 0,75. При двух подстанциях на каждой ма­гистрали с_н = 5 и Zxco/2 = 0,67. При с = со

Ехсо/2 = 0,5. Пределы возможного измене­ния Zxco/2 в формуле (13.90) от 1 до 0,5.

С помощью (13.7), (13.63), (13.69), (13.89) и (13.90) уравнение (13.88) может быть представлено в следующем виде:

3 = + М_{у с} <7_{Т с}т_? + (/, + £) х

х (a_llC[1 + + (/_{T с} + £)(аЕ/ + ЬМ). (13.91)

Для удобства дифференцирования выра­зим материальную характеристику сети М через удельное линейное падение давления £_л. Зададимся произвольным удельным ли­нейным падением давления вдоль расчет­ной магистрали £₀, проведем гидравличе­ский расчет всей тепловой сети, включая все ответвления от магистрали, и найдем ее материальную характеристику М_о.

При расчете М_о для сети с насосными подстанциями необходимо учитывать раз­мещение насосных подстанций вдоль сети, которое должно быть заранее выбрано или задано (см. рис. 13.4). При установке на ма­гистральной сети насосных подстанций располагаемые напоры в ответвлениях от магистрали меньше, чем в сети без насос­ных подстанций, при одном и том же значе­нии Rq. Поэтому материальная характери­стика сети Mq получается в сети с подстан­циями больше, чем в сети без подстанций.

Произведение M₀R₀’ для данной теп­ловой сети с заданным количеством насос­ных подстанций и заданным их расположе­нием является постоянной величиной, не зависящей от произвольно выбранного удельного линейного падения давления £₀.

О 19

Произведение MqRq является показате­лем, характеризующим разветвленность данной тепловой сети, распределение на ней насосных подстанций и распреде­ление расхода теплоносителя по отдельным участкам сети:

i=l

где .4 ® — см. табл 5.1; G_t — расход тепло­носителя на участке /; /₍ — длина участка /.

Поскольку для данной тепловой сети Л/_о/?о'¹⁹ = const, то ее материальная харак­теристика при любом линейном удельном падении давления Я., выразится уравнени­ем М= Л4₀(Л₀/Л_л)°’¹⁹.

Подставив указанную зависимость в (13.83), найдем по правилу нахождения экс­тремума функций производную с!3/с1Л_л и приравняем ее нулю.

После соответствующих преобразований получим выражение для оптимального удель­ного линейного падения давления, Па/м,

Я°^ПТ = f 190р<р^^°’³⁷ . (13.92)

При р = 975 кг/м где М_о — материальная характеристика се­ти, м²; R_o — удельное падение давления, Па/м; G — расход воды в сети, кг/с; L — длина главной магистрали (суммарная дли­на подающей и обратной линий), м; ф — ко­эффициент, зависящий от экономических показателей и оборудования сети, кВт/м²,

«_тс + Е)Ъ + 7_Т(Л_?

0 84

Второй множитель ф ' зависит от ха­рактеристики оборудования сети и насосных станций а, /г_и), q_tc, количества насосных станций и их размещения вдоль магистрали Ехш/2, стоимостных показателей />, й_н, т_т, т_э. При включении на магистральных сетях на­сосных подстанций Exto/2 < 1 и по сравне­нию с вариантом отсутствия насосных под­станций больше ф. Одновременно становит­ся больше значение MqRq’ ¹⁹ . Все это приво­дит к увеличению оптимального удельного линейного падения давления /?°^т .

При отсутствии на магистральной сети насосных подстанций Ехсо/2 = 1 и ф стано­вится практически постоянным, зависящим только от характеристик оборудования сети и насосной установки ТЭЦ Т)_ну, q_1Q, а, климатических условий, режима работы се­ти т_ср, т, п и стоимостных показателей

^11’ Э-

Оптимальное удельное линейное паде­ние давления, Па/м,

опт 0 19 0,84

R° = 17 8ОО(Л4_оЯ^9, ) .(13.94)

Приведенная методика исходит из по­стоянного удельного падения давления в главной магистрали, т.е. из прямолиней­ного пьезометрического графика главной магистрали. Такое распределение напора можно с достаточной точностью считать экономически оправданным [145].

Для определения ио изложенной мето­дике экономического падения давления по­ступают следующим образом:

задаются произвольным удельным паде­нием давления R_o;

проводят гидравлический расчет сети; на основании результатов гидравличе­

ского расчета находят материальную харак­теристику М_о, соответствующую удельно­му падению давления /?₀;

по (13.92) подсчитывают Л°^пт .

В том случае, когда оптимальное число насосных подстанций и их размещение вдоль магистрали являются искомыми па­раметрами, задаются различными вариан­тами количества и размещения насосных подстанций, для каждого из вариантов оп­ределяют Л°^пт по (13.92) и (13.93), расчет­ные затраты по (13.88) и выбирают вариант, отвечающий условию 3 - min.

Экономическое удельное падение давле­ния в транзитной магистрали, т.е. в магист­рали без ответвлений, Па,

Значение Л „ —см. табл. 5.1.

При эквивалентной шероховатости

А_э - 0,0005 м, = 117 • 10^—3

Я °"^т = 4390q>°’⁸⁴/G°’⁵².

Оптимальный диаметр транзитной маги­страли

_опт = 0,144(Л “ )°’⁸⁴С⁰'⁴⁸/ ф°’^{1 б}. (13.96) При = 0,0005 м, Я® = 117- 10"³

rf_onT= 0,024С°’⁴⁸/ф°’¹⁶. (13.96а)

Более подробно см. [101].

Транзитные теплопроводы. Транзит­

ные теплопроводы наиболее рационально выполнять без промежуточных насосных подстанций оптимальным диаметром, рас­считанным по (13.96), т.е. только с одной ос­новной насосной установкой в источнике те­плоснабжения, так как применение проме­жуточных подстанций приводит в этих усло­виях к увеличению расчетных затрат по насосным установкам, т.е. слагаемого (/_н + Е)К_Н в (13.88) или (13.91), при неизмен­ном значении всех остальных слагаемых рас­четных затрат.

Однако такое решение не всегда возмож­но. На гидравлические режимы транзитных тепловых сетей, особенно при большой их длине, часто накладываются ограничения по допустимым максимальным или мини­мальным давлениям из условий механиче­ской прочности, предупреждения вскипания теплоносителя, недопущения вакуума и др.

Для выполнения этих требований прихо­дится в длинных транзитных теплопрово­дах создавать насосные подстанции с тем, чтобы изменение пьезометрического напо­ра на участках теплопровода между двумя последовательно включенными подстан­циями не превышало некоторого заданного значения Д7/, м.

Метод определения оптимального коли­чества насосных подстанций на транзитной магистрали приведен в [101].

7.