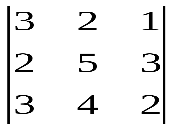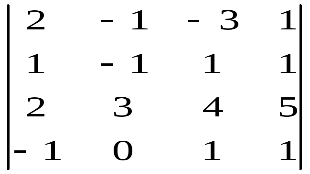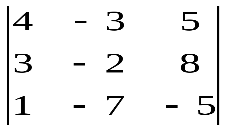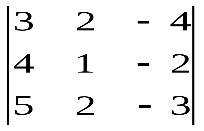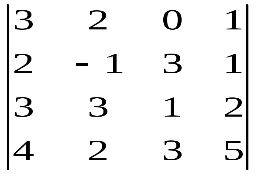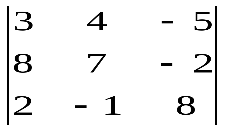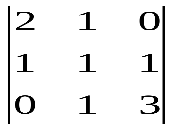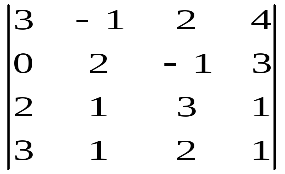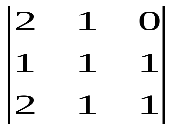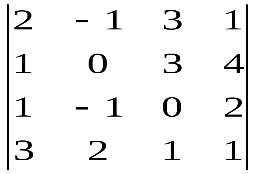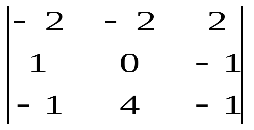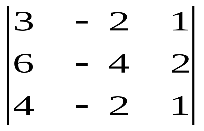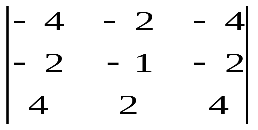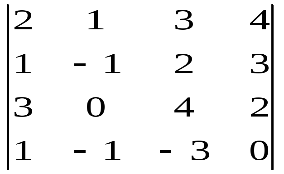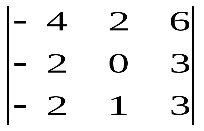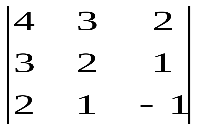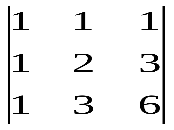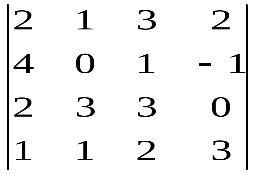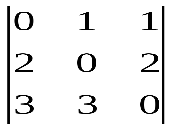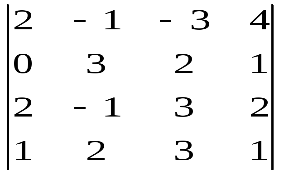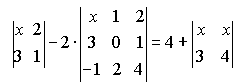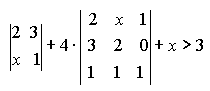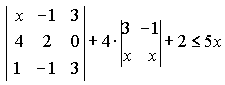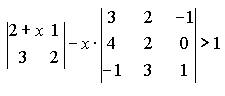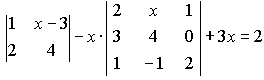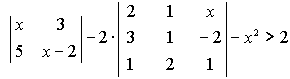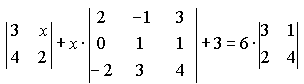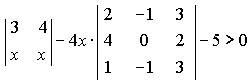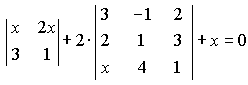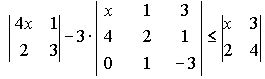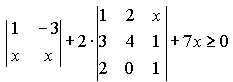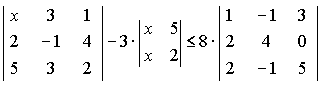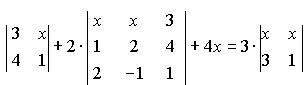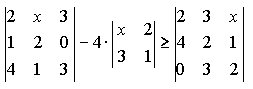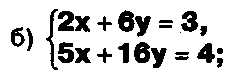Элективный курс. Элек курс Таня МПО-18. Институт математики и информатики Кафедра методики преподавания математики Элементы линейной алгебры
 Скачать 371.04 Kb. Скачать 371.04 Kb.
|
|
Министерство науки и высшего образования РФ Федеральное государственное автономное образовательное учреждение высшего образования «Северо-Восточный федеральный университет им. М.К. Аммосова» Институт математики и информатики Кафедра методики преподавания математики Элементы линейной алгебры Элективный курс Выполнил: студент группы ИМИ БА-МПО-18, Птицына Татьяна. Проверил: Скрябина Алевтина Гавриловна Якутск 2021 Аннотация элективного курса Предлагаемый элективный курс адресован учащимся 11 классов, планирующим в дальнейшем заниматься серьезной математикой и ее приложениями в различных научных областях. Данный курс позволит удовлетворить образовательные потребности учащихся, осваювающих как базовый уровень математики, так и профильный уровень. Пояснительная записка. Содержание курса соответствует целям предпрофильного обучения, который направлен на достижение нового качества обучения математике с учетом современных требований в условиях организации предпрофильной подготовки и введение профильного обучения, на предварительное самоопределение учащихся в отношении собственного профильного направления в образовании. Дает обучающимся возможность реализовать свой интерес к выбранному предмету; Помогает уточнить готовность и способность обучающихся осваивать выбранный предмет на повышенном уровне; Создает условия для подготовки к экзаменам по выбору (будущее профилирующие); Создает условия для осознанного и успешного выбора профиля выпускником школы. Цели курса: Дополнить базовую программу новыми понятиями, не нарушая ее целостности, расширяя и углубляя знания учащихся, воспитывая интерес к предмету через подачи материала, возможность свободного творчества. Задачи : Оказать педагогическую помощь в приобретении школьниками представлений, связанных с профессиональным становлением; Обеспечить индивидуализацию обучения; Дать возможность реализовать свои образовательные запросы; Формировать способности принимать адекватное решение о выборе дальнейшего направления образования, пути получения профессии. Уметь решать системы уравнений различными способами как школьного курса так и способами высшего образования (линейная алгебра); Уметь применять ЗУН при решении трудных заданий, практических задач. Преобладающие методы обучения: Проблемный; Исследовательский; Практикумы; Самостоятельная работа обучающихся; Лекционные занятия; Проектный; Предпрофильное обучение элективных курсов осуществляется в форме: Лекционных занятий; Практикумов; Защита рефератов. ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА.
Темы рефератов: Матрицы и действия над ними; Решение систем уравнений методом Крамера; Решение систем уравнений методом Гаусса; Решение систем уравнений матричным методом. Собственные векторы и собственные значения матриц; Определители. Свойства и вычисления. Системы уравнений и их способы решений. Технологическая карта практического занятия № 1 (1 пара - 90 мин).
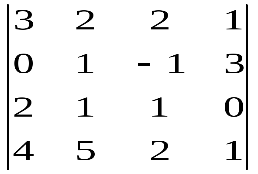
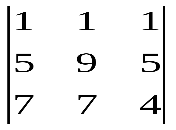
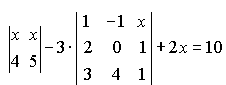
Варианты индивидуальных заданийЗадание 1.а),б) Вычислить указанные определители. в) Вычислить определитель четвертого порядка, предварительно преобразовав его так, чтобы три элемента некоторого ряда равнялись нулю, и разложить полученный определитель по элементам этого ряда.
Домашняя работа
Практикум. Задания по теме «Решение систем разными способами»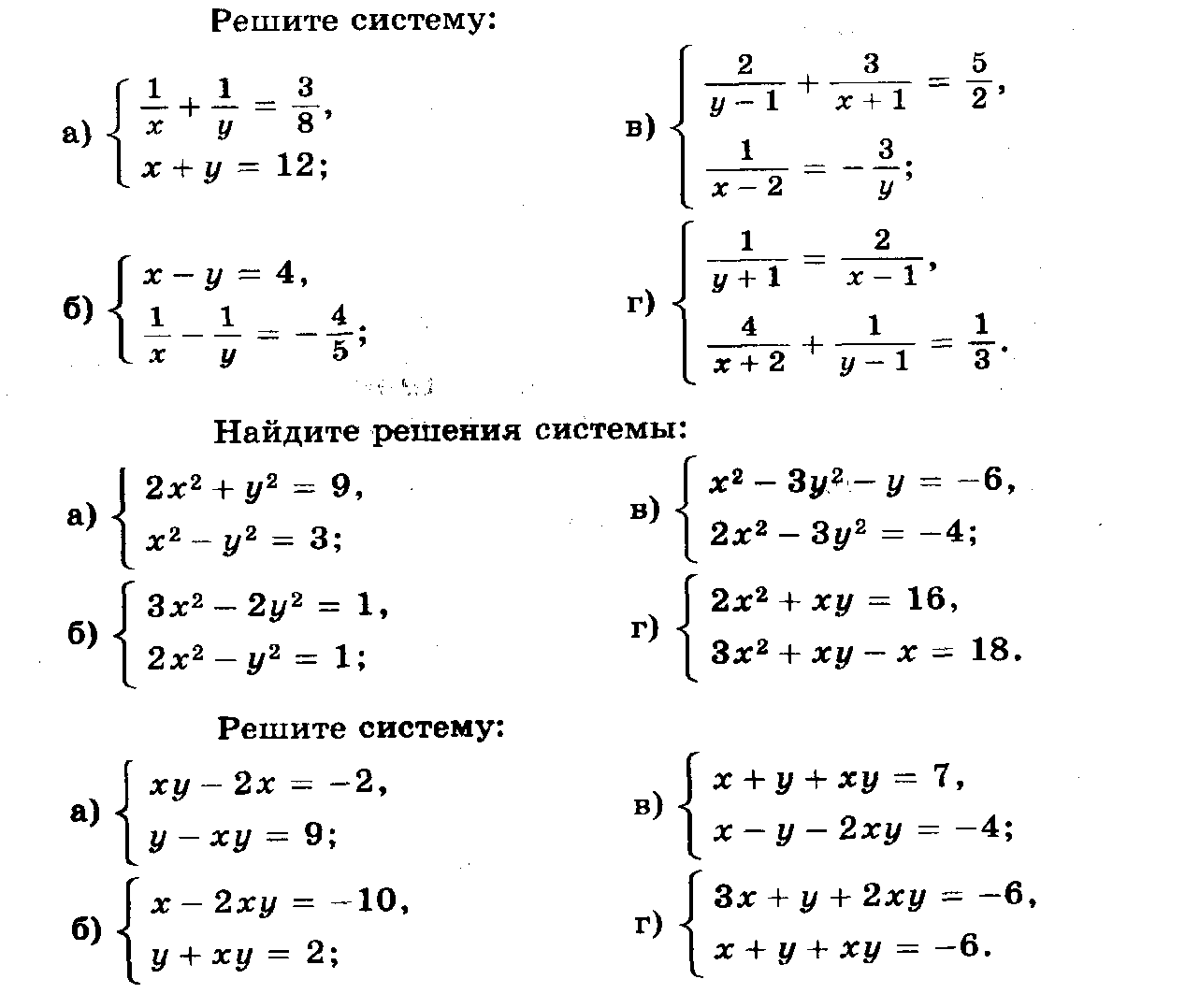 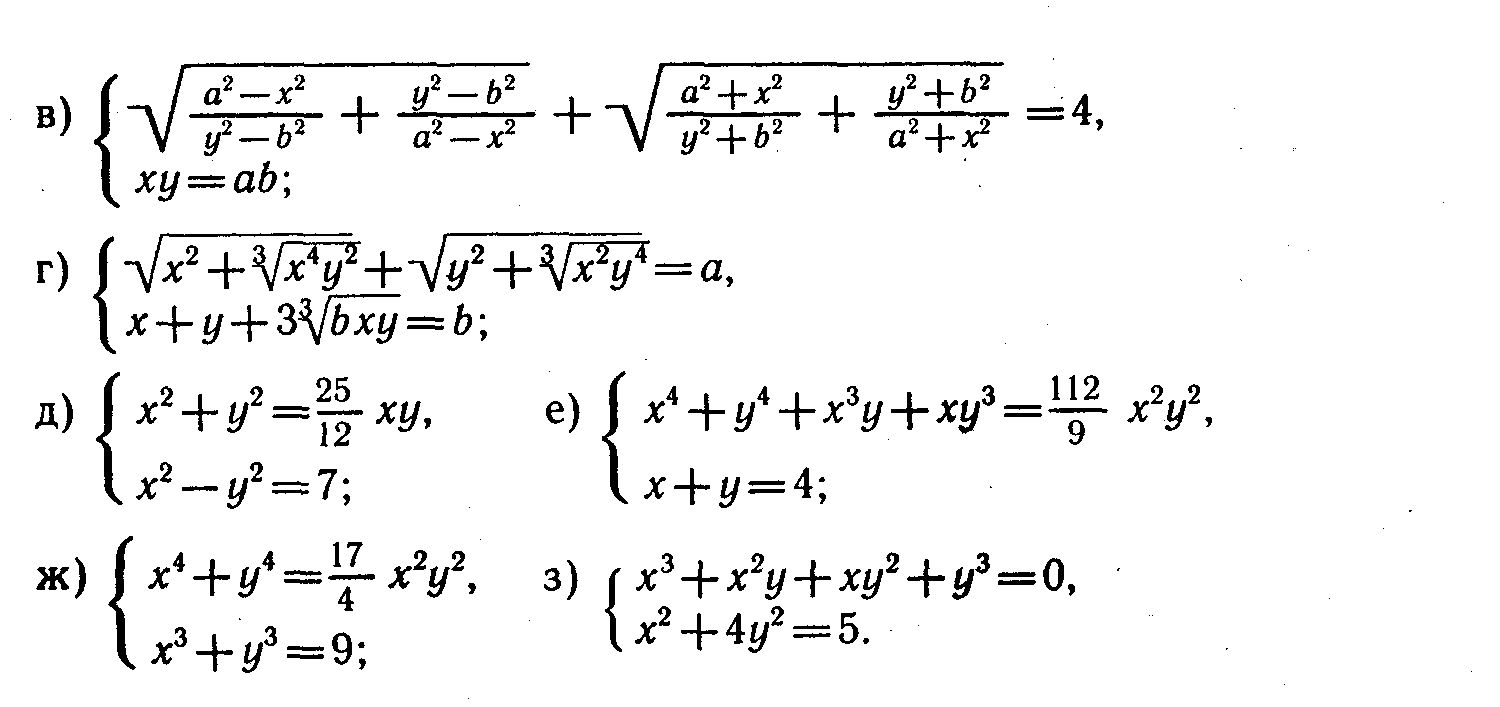 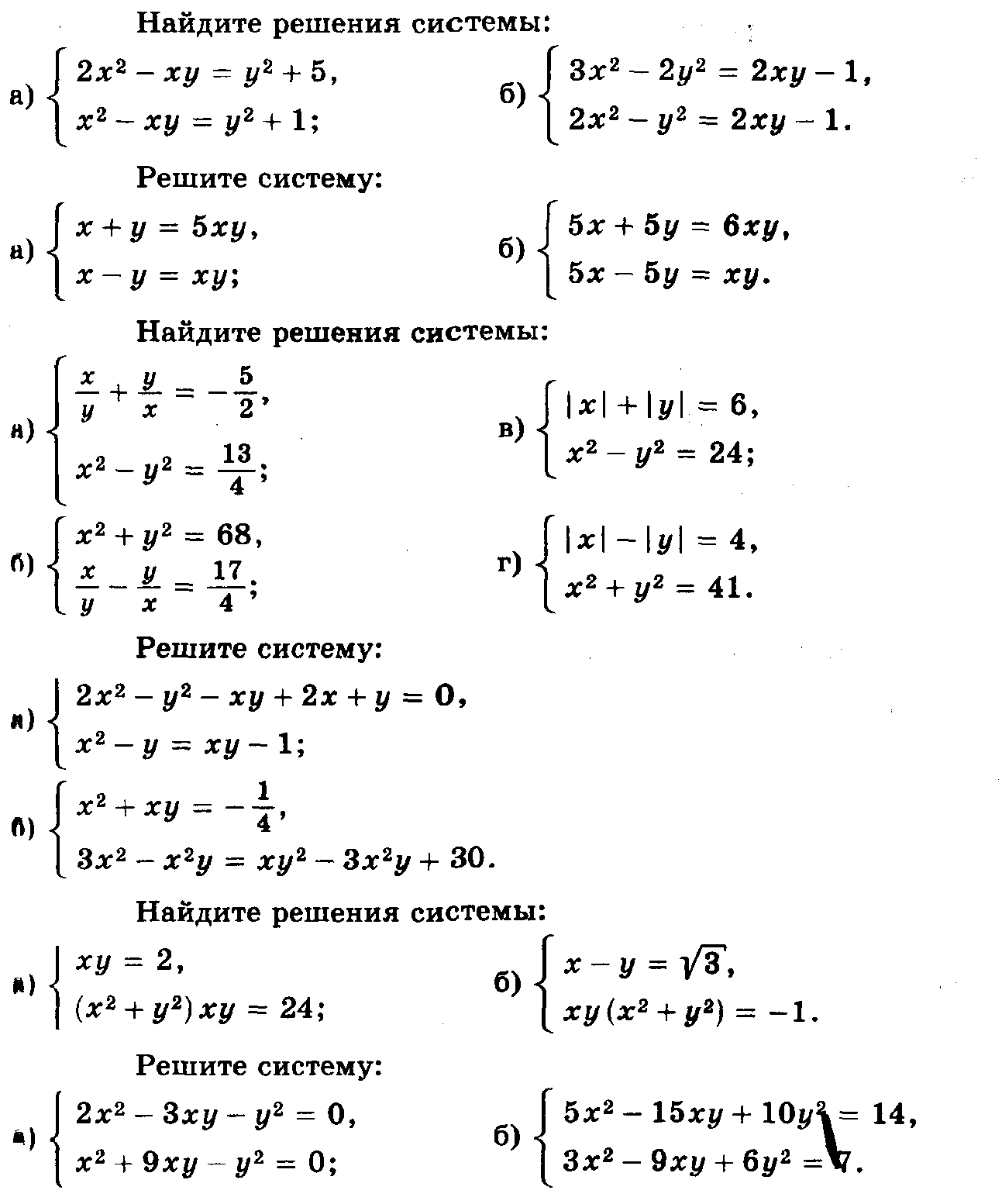 Задания по теме «Теорема Крамера»Задание. Заполните пропуски в таблице
Задание. Выясните, какие из следующих систем можно решить с помощью формул Крамера, и решите их, а если нет, то решите их любым другим способом: 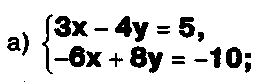 Задание. 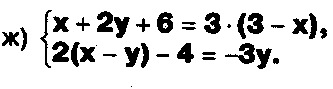 Даны системы. Не решая их, определите число решений, т.е. определите по внешнему виду систем, какие из них - совместные; несовместные; - определенные; - неопределенные? 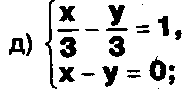 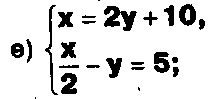 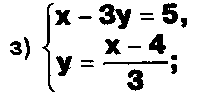 Задание. Вычислите определители матриц: 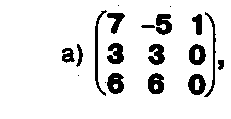 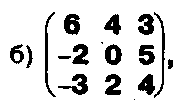 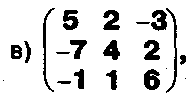 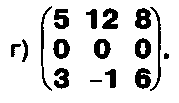 Задание. Решите системы: 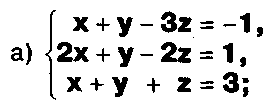 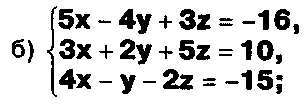 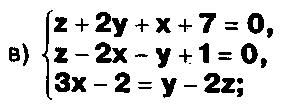 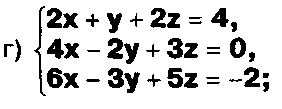 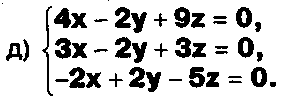 Задание. Даны системы. Не решая их, определите, какие из них являются совместными? Несовместными? Определенными? Неопределенными? Затем решите их. 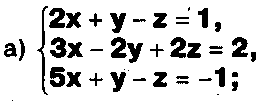 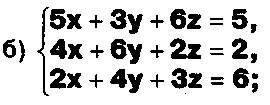 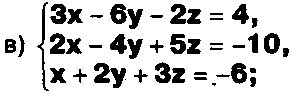 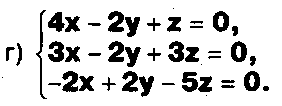 Задание. Дано одно уравнение системы, припишите к нему другое уравнение так, чтобы полученная система: - не имела решений; - имела единственное решение; - имела бесконечное число решений. 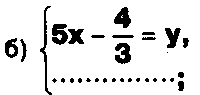 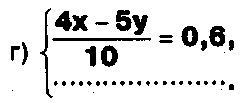 Задание. Может ли система а) иметь единственное решение; б) иметь бесконечное множество решений; в) не иметь решений? Какими должны быть коэффициенты в каждом возможном случае? Задание. Найти все значения параметра а, при которых система не имеет решений: 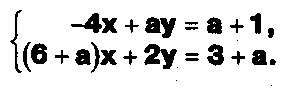 Задание 4. Дана система Найдите такие значения Ь, при которых система имела бы: - единственное решение, бесконечное число решений. Задание. а) Определите, при каких значениях параметра k система 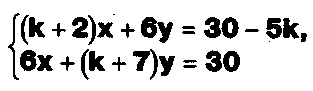 имеет бесконечное число решений. б) Определите, при каких значениях параметра k система 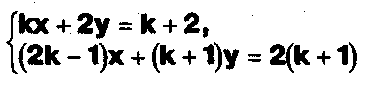 не имеет решений. Задание . . .Дана система с параметром а : Объясните предложенное решение: 1-й шаг. 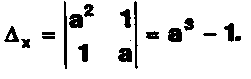 2-й шаг. 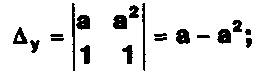 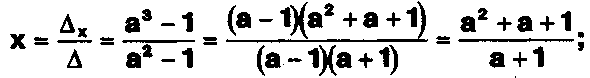 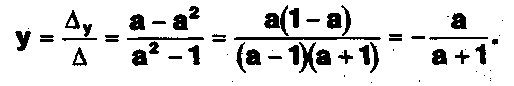 3-й шаг. 1 х + у = 1, у = 1 - х, х - любое; б)а = -1, Задание. Решите 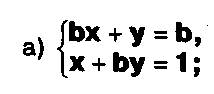 системы с параметром: системы с параметром: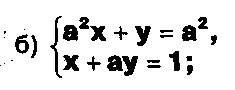 Задание. Найти все значения параметра с, при которых система не имеет решений: 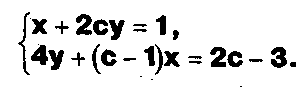 Задание. Решите систему с параметрами а и Ь: 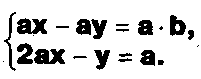 Задание. Решите систему используя параметр k. 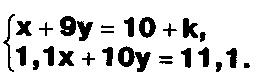 ЛИСТ КОНТРОЛЯ 1. Как вывести формулы Крамера для решения системы двух линейных уравнений с двумя неизвестными? 2. Как решать систему двух линейных уравнений с двумя неизвестными, если нельзя пользоваться формулами Крамера? 3.Какая система линейных уравнений называется совместной? несовместной? определенной? неопределенной? 4.Как формулируется теорема Крамера? 5.Как вычислить определитель второго порядка? 6. Как вычислить определитель третьего порядка? 7. В каком случае система двух линейных уравнений с двумя неизвестными имеет единственное решение? 8.В каком случае система трех линейных уравнений с тремя неизвестными имеет единственное решение? 9.В каком случае система двух линейных уравнений с двумя неизвестными имеет бесконечное число решений? 10.В каком случае система трех линейных уравнений с тремя неизвестными имеет бесконечное число решений? 11.В каком случае система двух линейных уравнений с двумя неизвестными не имеет решений? 12.В каком случае система трех линейных уравнений с тремя неизвестными не имеет решений ? 13. Как решать определенную систему трех линейных уравнений с тремя неизвестными? 14.Что называется решением уравнения с n неизвестными? 15. Как решать уравнение с n неизвестными, если хотя бы один из коэффициентов при неизвестных отличен от нуля? Задания по теме «Метод Гаусса»ЗАДАНИЕ . Решите системы уравнений: 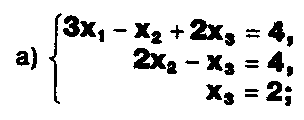 *• * *• *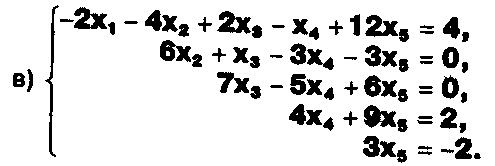 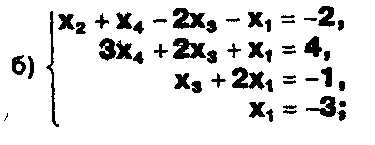 ЗАДАНИЕ . а) Прокомментируйте 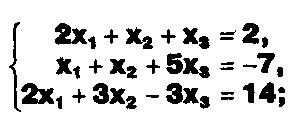 решение системы: решение системы: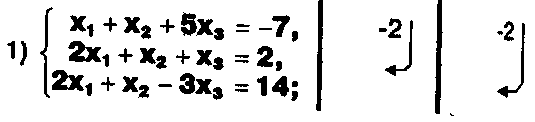 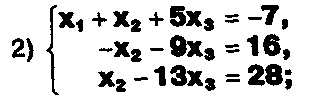 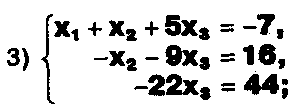 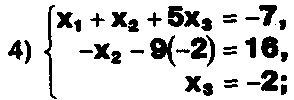 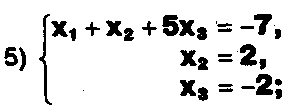 x1 = 1, 6) x2= 2, x3 = -2. б) Решите систему 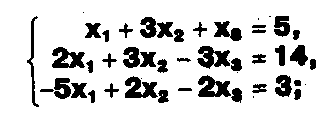 в)Равносильны ли системы а) и б)? ЗАДАНИЕ . а) Решите системы уравнений: 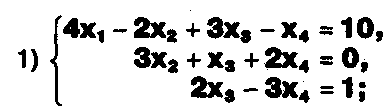 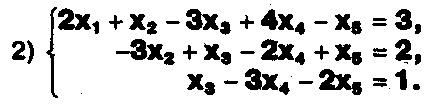 б) Составьте аналогичные по внешнему виду системы из трех уравнений с четырьмя, пятью и шестью неизвестными и решите их. ЗАДАНИЕ . При решении систем методом Гаусса были получены системы: 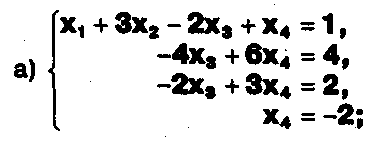 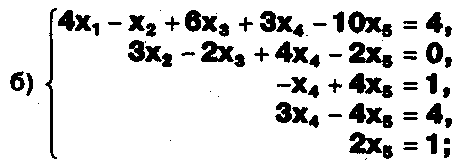 Можно ли утверждать, что первая система совместна и неопределенна, а вторая - несовместна? Закончите решения этих систем. ЗАДАНИЕ . а) Решите систему 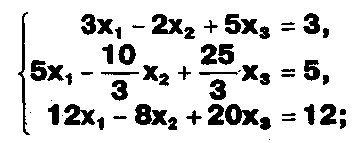 б) Верно ли, что система из а) равносильна системе 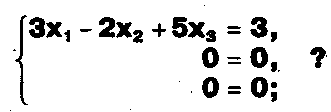 в) Верно ли, что система из а) равносильна системе, имеющей общее решение: 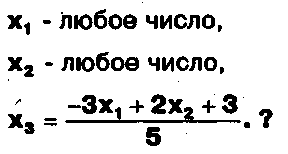 ЗАДАНИЕ . Решите системы уравнений: 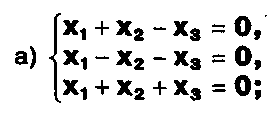 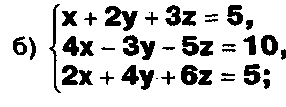 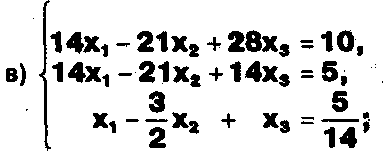 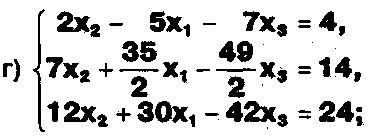 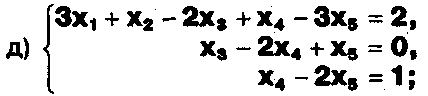 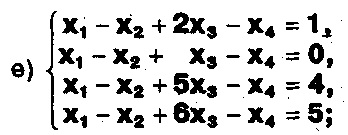 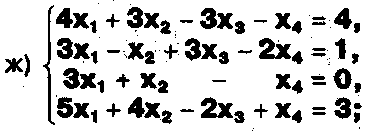 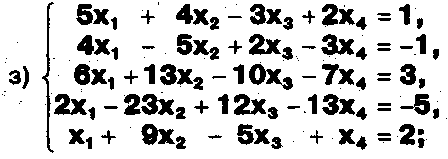 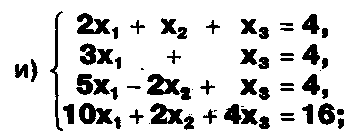 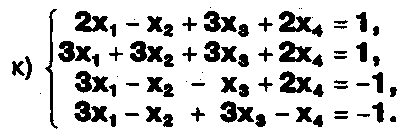 ЗАДАНИЕ . Решите системы уравнений: 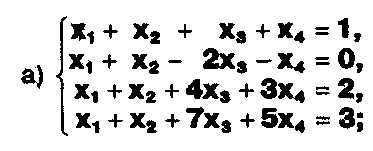 ? ?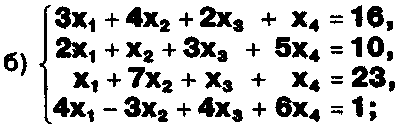 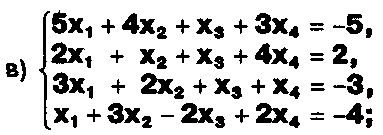 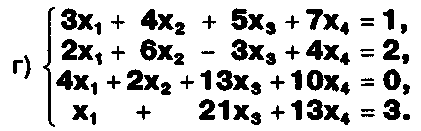 ЗАДАНИЕ . Доказать, что система уравнений 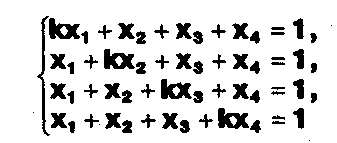 при k, отличном от 1 и -3, имеет единственное решение. ЗАДАНИЕ. Доказать, что система уравнений 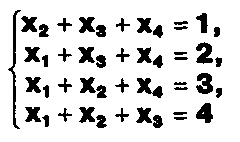 имеет единственное решение. Найти это решение. ЗАДАНИЕ . Доказать, что система уравнений 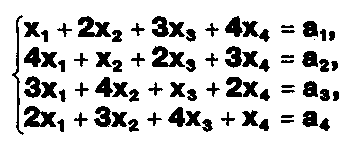 имеет единственное решение. Найти это решение. ЗАДАНИЕ . При каком условии система уравнений 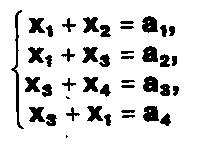 ; ;имеет единственное решение? Найти это решение. ЗАДАНИЕ. Доказать, что система уравнений 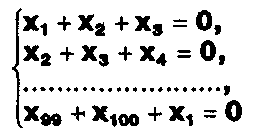 имеет единственное нулевое решение (т.е. x1 = х2 =К = х100 = О). ЛИСТ КОНТРОЛЯ. 1.Какие две системы называются равносильными? 2. Каковы способы перехода к равносильным системам? 3. В чем состоит прием доказательства равносильности двух систем? 4. Как можно проверить равносильность определенных систем? 5.Как можно проверить равносильность неопределенных систем? 6.Каким методом можно решить системы линейных уравнений с любым числом неизвестных? 7. В чем состоит метод Гаусса? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||