Статистика. Решение Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда
 Скачать 433.17 Kb. Скачать 433.17 Kb.
|
|
Задание 1 Имеются данные о числе тонн грузов, перевозимых еженедельно паромом некоторого морского порта в период навигации: 398, 412, 504, 474, 544, 690, 641, 600, 613, 457, 504, 477, 530, 641, 359, 641, 452, 633, 474, 641, 580, 504, 344, 455, 505, 396, 347, 504, 390, 504, 400, 641. Построить статистический ряд; Построить полигон распределения. Найти среднее арифметическое, дисперсию, среднее квадратическое отклонение, моду и медиану. Построить вариационный ряд, полигон частот распределения, интервальный статистический ряд, гистограмму. Найти моду, медиану, среднее арифметическое, дисперсию, среднее квадратическое отклонение. Решение: Построим дискретный вариационный ряд. Для этого отсортируем ряд по возрастанию и подсчитаем количество повторения для каждого элемента ряда.
Таблица для расчета показателей.
Для оценки ряда распределения найдем следующие показатели: Показатели центра распределения. Средняя взвешенная (выборочная средняя) Мода. Мода - наиболее часто встречающееся значение признака у единиц данной совокупности. Имеются два показателя с одинаковым значением частоты f=5. Ряд имеет две моды, т.е. является бимодальным. Медиана. Медианой (Me) называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Находим xi, при котором накопленная частота S будет больше ∑f/2 = 17. Это значение xi = 504. Таким образом, медиана равна 504. Медиана служит хорошей характеристикой при ассиметричном распределении данных, т.к. даже при наличии "выбросов" данных, медиана более устойчива к воздействию отклоняющихся данных. В симметричных рядах распределения значение моды и медианы совпадают со средней величиной (xср=Me=Mo), а в умеренно асимметричных они соотносятся таким образом: 3(xср-Me) ≈ xср-Mo Показатели вариации. Абсолютные показатели вариации. Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда. R = xmax - xmin = 690 - 344 = 346 Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности. Каждое значение ряда отличается от другого в среднем на 81.211 Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего). Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия). Среднее квадратическое отклонение. Каждое значение ряда отличается от среднего значения 507.969 в среднем на 98.428 Оценка среднеквадратического отклонения. Относительные показатели вариации. К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение. Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс. Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять. Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины. Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней. Показатели формы распределения. Степень асимметрии. Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой. Наиболее точным и распространенным показателем асимметрии является моментный коэффициент асимметрии. As = M3/s3 где M3 - центральный момент третьего порядка. s - среднеквадратическое отклонение. M3 = 3159335.47/32 = 98729.23 Положительная величина указывает на наличие правосторонней асимметрии Оценка существенности показателя асимметрии дается с помощью средней квадратической ошибки коэффициента асимметрии: 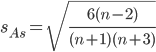 Если выполняется соотношение |As|/sAs < 3, то асимметрия несущественная, ее наличие объясняется влиянием различных случайных обстоятельств. Если имеет место соотношение |As|/sAs > 3, то асимметрия существенная и распределение признака в генеральной совокупности не является симметричным. Расчет центральных моментов проводим в аналитической таблице:
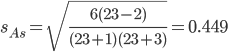 В анализируемом ряду распределения наблюдается несущественная асимметрия (0.104/0.449 = 0.23<3) Применяются также структурные показатели (коэффициенты) асимметрии, характеризующие асимметрию только в центральной части распределения, т.е. основной массы единиц, и независящие от крайних значений признака. Рассчитаем структурный коэффициент асимметрии Пирсона: Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения. Чаще всего эксцесс оценивается с помощью показателя: Для распределений более островершинных (вытянутых), чем нормальное, показатель эксцесса положительный (Ex > 0), для более плосковершинных (сплюснутых) - отрицательный (Ex < 0), т.к. для нормального распределения M4/s4 = 3. M4 = 5763102809.4/32 = 180096962.79 Число 3 вычитается из отношения μ4/ σ4 потому, что для нормального закона распределения μ4/ σ4 = 3. Таким образом, для нормального распределения эксцесс равен нулю. Островершинные кривые обладают положительным эксцессом, кривые более плосковершинные - отрицательным эксцессом. Ex < 0 - плосковершинное распределение Чтобы оценить существенность эксцесса рассчитывают статистику Ex/sEx где sEx - средняя квадратическая ошибка коэффициента эксцесса. 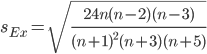 Если отношение Ex/sEx > 3, то отклонение от нормального распределения считается существенным. 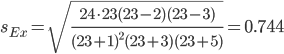 Ex/sEx = -1.08/0.744 = 1.452 Поскольку sEx < 3, то отклонение от нормального распределения считается не существенным. Доверительный интервал для дисперсии. Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = γ/2 = 0.023. Для количества степеней свободы k=n-1=31, по таблице распределения χ2 находим: χ2(31;0.023) = 53.20335. Случайная ошибка дисперсии нижней границы: Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.023 = 0.977: χ2(31;0.977) = 18.50893. Случайная ошибка дисперсии верхней границы: Таким образом, интервал (5827.09;16749.81) покрывает параметр S2 с надежностью α = 0.046 (γ=95.4%) Доверительный интервал для среднеквадратического отклонения. S*(1-q) < σ < S*(1+q) Найдем доверительный интервал для среднеквадратического отклонения с надежностью γ = 0.954 и объему выборки n = 32 По таблице q=q(γ ; n) определяем параметр q(0.954;32) = 0.26 100.003(1-0.26) < σ < 100.003(1+0.26) 74.002 < σ < 126.004 Таким образом, интервал (74.002;126.004) покрывает параметр σ с надежностью γ = 0.954 Выводы: Каждое значение ряда отличается от среднего значения 507.969 в среднем на 98.428. Поскольку коэффициент вариации меньше 30%, то совокупность однородна. Полученным результатам можно доверять. Значения As и Ex мало отличаются от нуля. Поэтому можно предположить близость данной выборки к нормальному распределению. Полигон 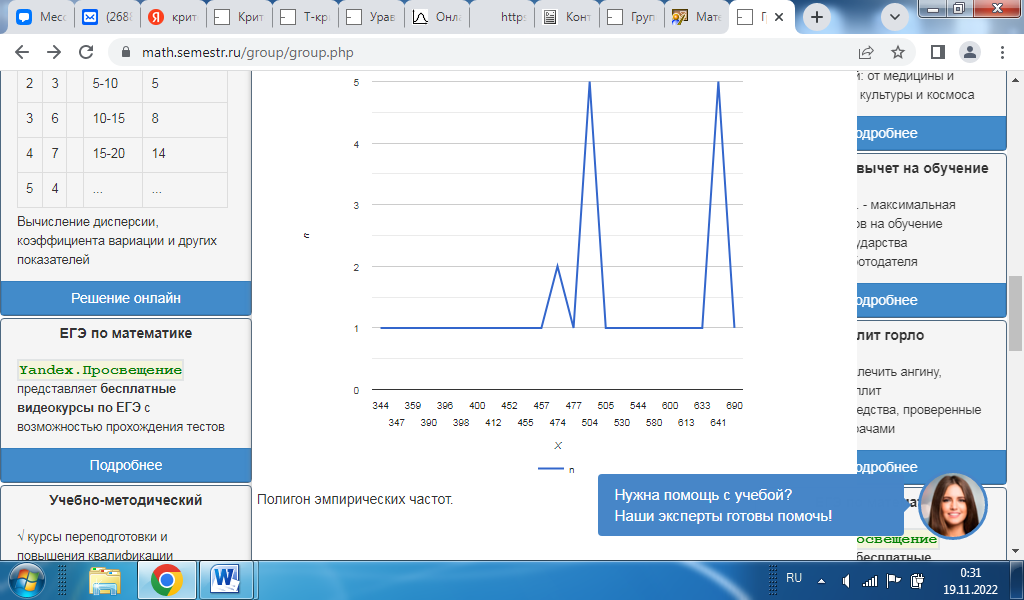 Полигон эмпирических частот 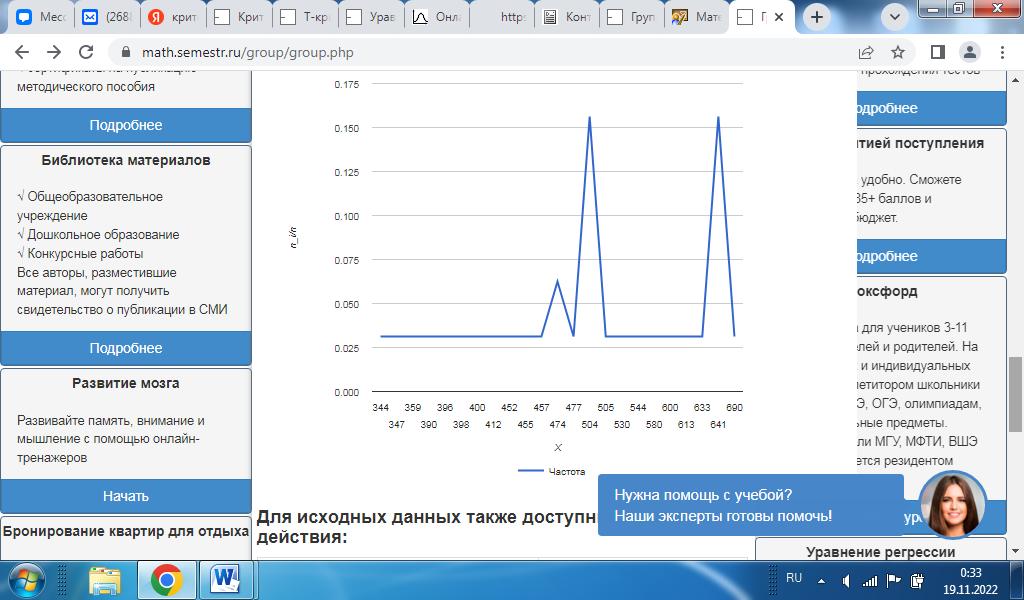 |
