Психология творчества. Пономарев Я.А. - Психология творчества. Институт психологии я. А. Пономарев психология творчества

• Название: Институт психологии я. А. Пономарев психология творчества
• Анкор: Психология творчества
• Дата: 30.09.2022
• Размер: 1.84 Mb.
• Имя файла: Пономарев Я.А. - Психология творчества.doc
• Тип: Книга; #706801
• страница: 20 из 25

Рис. 18



было усложнено, хотя общий принцип этих задач оставался адекватным образующей задаче и задаче-индикатору.

Одной группе испытуемых (10 человек) в качестве стимулирующей задачи была предложена задача «16 точек»; другой группе, также состоящей из 10 человек, — задача «9 точек». Задача-индикатор и образующая задача в обеих группах оставались одни и те же.

В итоге опытов были получены следующие результаты. В группе испытуемых, где в функции стимулирующей задачи использовалась задача «16 точек», ни один из 10 человек не нашел решения задачи-индикатора. В этой группе, где стимулирующей задачей была «9 точек», решение задачи-индикатора нашли 2 человека (из 10 испытуемых).

Таким образом, в группе, где стимулирующая задача обладала максимумом сложности, побочный продукт действия в ситуации образующей задачи не помог решению индикатора. Однако минимальное (говоря о максимальном и минимальном усложнении стимулирующей задачи, мы имеем в виду, разумеется, данный частный случай) усложнение стимулирующей задачи (вторая группа опытов) сохраняло некоторую возможность решения задачи-индикатора.

Следовательно, усложнение содержания стимулирующей задачи приводит в целом к резкому снижению эффективности образующей задачи.

Поэтому в подлинном творчестве на первых его этапах надо стремиться к предельному упрощению вопроса и его предельной схематизации. Не этой ли именно необходимости отве-

223

чает столь широко распространенное сейчас всякого рода моделирование?

В следующей серии опытов использовались все те же задачи, с той лишь разницей, что усложненные задачи («9 точек» и «16 точек») выступали теперь не в функции стимулирующих задач, а в функции индикаторов.

Как и в предшествующих опытах, в экспериментах принимали участие двадцать испытуемых, разделенные на две группы (по 10 человек в каждой). Первой группе испытуемых в качестве задачи-индикатора предлагалось «9 точек»; второй группе—«16 точек».

В опытах с первой группой испытуемых 4 человека (из 10) нашли решение задачи-индикатора. Однако из анализа чертежей поисков решения задачи-индикатора этими испытуемыми и из последующей беседы с ними выяснялось, что решение задачи-индикатора «9 точек» было достигнуто не непосредственно, а опосредствованно, т. е. промежуточным путем. Вначале была решена стимулирующая задача «4 точки» (испытуемые проделали это по собственной инициативе, «с места», т. е. еще в ходе решения образующей задачи), а затем принцип ее решения был приложен к решению «9 точек», и после серии обычных для этого случая проб было найдено решение задачи-индикатора.

Опыты со второй группой испытуемых, где в качестве задачи-индикатора использовалась «16 точек», послужили в некоторой степени контролем к сделанному нами заключению по опытам с первой группой испытуемых. В этих опытах ни один из 10 человек не нашел решения задачи-индикатора, что полностью подтвердило высказанное ранее соображение, так каю двойное опосредствование было, разумеется, невыполнимой задачей.

Обсуждая результаты этих опытов, необходимо напомнить, что в данном случае отсутствие решения индикатора не могло быть следствием того, что побочный продукт действия в ситуации образующей задачи не выявлялся. На основании всех предшествующих опытов можно утверждать, что в данных условиях такое выявление было (хотя бы у некоторых испытуемых). Об этом же самом говорят и факты решения задачи-индикатора «9 точек» четырьмя испытуемыми. Действуя в оптимально благоприятных условиях в ситуации образующей задачи под влиянием стимулирующей задачи «4 точки», испытуемый осуществлял необходимую в этом случае ориентировку по побочному продукту. Однако, наталкиваясь в ситуации задачи-индикатора на дополнительные трудности, он не мог немедленно реализовать «подхваченный» в образующей ситуации принцип решения, в силу чего его относительно адекватные действия вовремя не подкреплялись и отбрасывались. Этим самым терялось и влияние побочного продукта действия,

224

Следовательно, одним из условий, способствующих использованию побочного продукта действия как способа решения творческой задачи, оказывается адекватность стимулирующей, образующей и выявляющей ситуаций и их возможная простота.

Этот вывод в практическом смысле требует в условиях творческого мышления максимальной предварительной логической обработки имеющихся данных, их максимального предварительного упрощения.

Затрагиваемый вопрос, как и аналогичный, ему предшествующий, также имеет общепсихологический смысл. В психологии нередко высказывались принципиальные возражения против всякого рода моделирования, против создания искусственных экспериментальных ситуаций, против использования экспериментальных задач, не имеющих места в реальной практике людей, и выдвигались требования изучать явления, непосредственно взятые из практики. Обнаруженные нами факты показывают, что моделирование в психологии как прием научного исследования в большинстве случаев совершенно необходимо для изучения событий реальной жизни; оно является одним из не-> обходимых промежуточных этапов вскрытия закономерностей, имеющих место в естественной практике людей.

Исследуя условия эффективности образующей задачи, мы натолкнулись еще на две группы явлений. Во-первых, было подмечено, что решение задачи-индикатора оказывается зависимым от того, каким способом выполняется образующая задача. Во-вторых, были также подмечены и несколько иные об-стоятельства, в которых решающее значение имела характеристика не того способа, которым выполнялась образующая задача, а того, в который преобразовывался в ситуации задачи-индикатора содержащийся в этой задаче побочный продукт действия.

В первом случае успех оказался зависимым от степени автоматизированное™ того способа действия, которым выполнялась образующая задача; во втором случае этот успех оказался связанным со степенью абстракции того способа, в который преобразовывался в ситуации задачи-индикатора побочный продукт действия.

В первой части этой серии опытоз в качестве стимулирующей задачи использовались «4 точки», в качестве образующей— «хальма» (условие описано на с. 215) и, наконец, в функции индикатора — вновь «4 точки».

Как и в прошлых опытах, здесь принимали участие две группы испытуемых. Однако в отличие от предшествующих опытов различия между экспериментами в разных группах состояли не в том, что испытуемым этих групп давались разные задачи (наоборот, задачи во всех случаях были совершенно одинаковыми), — различными были категории испытуемых, подобранные в эти группы. Испытуемые первой группы уже давно уме-

225



ЛИ Играть в «хальму» и достаточно владели ее правилами; испытуемые второй группы, наоборот, были подобраны так, что ни один из них до этого не имел об этой игре никакого представления. Этих испытуемых приходилось обучать правилам игры.

Легко догадаться, что у первых способ выполнения образующей задачи был в значительной степени автоматизированным, в то время как у вторых такой автоматизации никак не могло быть, поскольку они только что овладели знаниями о правилах ходов при игре в «хальму».

Порядок предъявления заданий во всех опытах был «обратным» (стимулирующая задача — образующая задача — задача-индикатор). Во всех случаях мы старались создать для испытуемых обеих групп тождественные условия эксперимента.

В результате экспериментов оказалось, что испытуемые первой группы, выполнявшие образующую задачу глубоко автоматизированными и узко специализированными действиями, дали меньшее количество решений задачи-индикатора, чем представители второй группы, не умевшие до этого играть в «хальму» и, следовательно, не использовавшие при выполнении предварительной задачи автоматизированные и специализированные действия.

Чтобы исключить возможный элемент случайности данного результата, мы решили повторить опыты с другими двумя группами испытуемых, используя при этом теперь уже различные предварительные задачи.

Во второй части опытов в качестве стимулирующей задачи использовались «4 точки»; в качестве образующей — «ферзь и пешки» (см. с. 221) и «вымышленная фигура»³ (рис. 19); в функции индикатора — вновь «4 точки». При прочих равных условиях одной группе испытуемых предлагалась задача «ферзь и пешки», другой — «вымышленная фигура».

На основании специальных опытов было установлено, что образующая задача «вымышленная фигура» вдвое эффективнее задачи «ферзь и пешки».

Рис. 19

Фигура, стоящая на поле d6 или d4 (рис. 19), должна снять тремя ходами три (или четыре) пешки. Правила ходов этой фигурой таковы: сняв пешку, она не встает на ее место, а проходит дальше; фигура действует но вертикалям и горизонталям как ладья, по диагоналям — цак слон.

226

Различия в эффективности этих образующих задач выступили еще более ярко, когда мы сопоставили во вновь проделанных опытах количество решений индикатора «4 точки», полученных при этих образующих задачах в разных группах испытуемых в течение двух первых минут поиска решения задачи-индикатора (опыты ставились так: вначале испытуемые обращались к стимулирующей задаче, затем испытуемым первой группы давалась образующая задача «ферзь и пешки», а испытуемым второй группы — «вымышленная фигура»; после выполнения этих заданий испытуемые обеих групп обращались к задаче-индикатору «4 точки»; через две минуты после этого опыт прекращался и регистрировалось количество полученных решений задачи-индикатора испытуемыми в той и другой группе).

Результаты опытов оказались следующими: из 10 испытуемых, использовавших образующую задачу «ферзь и пешки», задачу-индикатор решили лишь два человека; из 10 испытуемых, решавших образующую задачу «вымышленная фигура», задачу-индикатор решили 6 человек. Таким образом, задача «вымышленная фигура» оказалась в три раза эффективнее задачи «ферзь и пешки».

Различия в эффективности этих задач в данном случае могли быть объяснены только различиями в самих образующих задачах. Способ действия, которым выполнялась задача «ферзь и пешки», конечно, был значительно более автоматизирован, чем тот, которым пользовались испытуемые, решая задачу «вымышленная фигура»: в первой задаче мы использовали те действия, которые вырабатывались у испытуемых в течение нескольких лет игры в шахматы; во второй задаче мы умышленно видоизменили правила ходов, нарушив тем самым сложившиеся автоматизмы.

Следовательно, чем более автоматизировано и специализировано было действие, которым выполнялось решение образующей задачи, тем менее успешным было использование побочного продукта действия, и наоборот.

В другой серии опытов в функциях стимулирующей задачи и индикатора использовалась та же самая задача — «4 точки». Своеобразие этой серии состояло в образующей задаче: описать около квадрата треугольник.

В остальном опыты проводились точно таким же образом, как и в других сериях: вначале давалась стимулирующая задача, затем образующая и, наконец, задача-индикатор.

Прежде чем приступать к прослеживанию выполнения всего порядка задач, надо охарактеризовать образующую задачу.

Испытуемому давался квадрат с двенадцатью точками и таблица с двенадцатью квадратами; задание заключалось в том, чтобы описать на таблице около каждого квадрата треугольник, начиная построение треугольника из точки, номер

227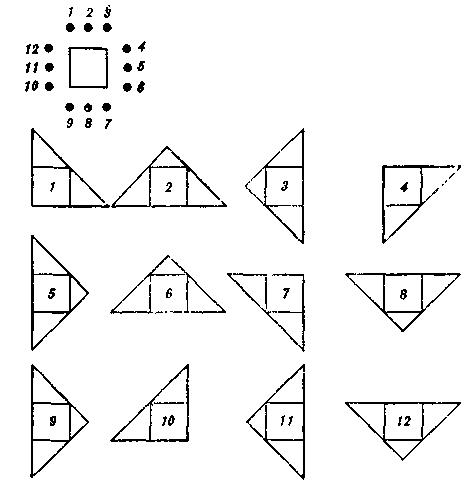



Рис. 20

которой соответствовал номеру квадрата (рис. 20), не допуская точного повторения чертежа ни в одном случае. Упражнения повторялись до тех пор, пока выполнение их не становилось прочно закрепленным, автоматизированным. Выработка автоматизма давала право считать данное задание по этому параметру нивелированным с задачей «ферзь и пешки».

После этого (в ряде случаев через несколько дней) мы приступили к основным опытам. Результаты оказались следующими: все 10 испытуемых нашли решение задачи-индикатора, затрачивая на поиски не более 1 минуты. Образующая задача «описать около квадрата треугольник» оказалась наиболее эффективной из всех использованных нами до этого подобных задач.

Как уже отмечалось, до основных опытов с целью нивелировки параметра автоматизации способа действия, которым выполнялось это задание, мы проводили с испытуемыми довольно продолжительные упражнения. Можно было предположить, что по ряду причин именно эти предварительные упражнения сыграли известную роль в столь высокой эффективности данной образующей задачи. Для выяснения возникшего вопроса была проведена контрольная серия опытов, в которой при прочих равных условиях испытуемые не проделывали предварительных упражнений, а прямо выполняли обычный порядок решения задач (стимулирующая — образующая — индикатор). Результаты контрольной серии опытов почти не отличались от

228

предшествующих. Таким образом, версия о зависимости высокой эффективности данного упражнения от предшествующих упражнений была исключена и причину такой эффективности следовало видеть в особенностях самой образующей задачи.

Причина высокой эффективности заключалась, видимо, в том, что в результате решения задачи «описать около квадрата треугольник» у испытуемого складывался тот побочный продукт, который в ситуации образующей задачи преобразовывался в широко обобщенное общественным опытом людей геометрическое правило (все испытуемые, участвовавшие в этой серии опытов, были достаточно хорошо знакомы с геометрией), которое уже ранее было усвоено испытуемыми как глубоко абстрагированное геометрическое понятие.

Таким образом, исследование моделей интуитивных решений привело к установлению ряда закономерностей таких решений: интуитивное решение возможно лишь в том случае, если ключ к нему уже содержится в неосознаваемом опыте; такой опыт малоэффективен, если он сложился в действиях, предшествующих попыткам решить творческую задачу; он становится эффективнее, формируясь на фоне целевой, поисковой доминанты; его эффективность возрастает, когда исчерпываются неправильные приемы решения задачи, но еще не гаснет поисковая доминанта; влияние неосознаваемой части действия тем эффективнее, чем менее содержательна сама по себе его осознаваемая часть; усложнение ситуации, в которой приобретается неосознаваемый опыт, препятствует его последующему использованию; аналогичное усложнение самой задачи также действует отрицательно; успех решения связан со степенью автоматизации способов действий, в ходе которых складывается необходимый неосознаваемый опыт — чем менее автоматизирован этот способ, тем больше шансов к успеху; чем к более общей категории можно отнести итоговое решение творческой задачи, тем вероятнее нахождение такого решения.

Модели логичных решений

Закономерности, перечисленные нами в предшествующем разделе, наиболее жестко связаны с получением интуитивного эффекта. Они отчетливо проявляются в ситуациях, объемная сложность которых минимальна, а найденный способ решения совпадает (или почти совпадает) с самим решением, т. е. не возникает необходимости в специальной реализации этого способа, связанной с превращением его в принцип. Такие задачи, оставаясь творческими, не являются проблемными. В проблемных ситуациях полученное решение одной простейшей познавательной задачи должно быть вновь использовано как принцип действия в другой, более сложной ситуации. Однако способ

229

действия, выработанный в итоге решения исходной задачи, вначале еще очень ограничен и непосредственно приводит к успеху только в весьма 'близкой ситуации. Действия на этой ступени еще недостаточно абстрагированы. Для превращения частного способа в принцип надо углубить уровень абстракции, «отфильтровать» действие, объективно содержащее принцип, от чувственных элементов ситуации, зачастую случайных, т. е. в известном смысле формализовать интуитивно полученный эффект.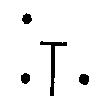

Рис. 21

Конкретным материалом экспериментального исследования послужил специально разработанный нами цикл задач-звеньев, в основу построения которого был положен принцип решения одной из известных задач — головоломок. С некоторыми задачами этого цикла мы познакомились уже в предшествующих разделах. Здесь мы приводим их полное систематическое описание.

Простейшая и вместе с тем исходная задача этого цикла была названа задачей «трех точек» (I). Условия задачи «трех точек» таковы: соединить три точки двумя прямыми линиями, не пересекая Т-образной преграды (рис. 21).

Второй по порядку задачей была известная нам «4 точки» (II).

Третьей была только что описанная в предшествующем разделе задача «9 точек» (III) ⁴.

Четвертая задача — также знакомая нам — «16 точек» (IV).

Пятая задача — «25 точек» (V): даны 25 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, восемь прямых линий.

Шестая задача — «36 точек» (VI): даны 36 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, 10 прямых линий.

Седьмая задача — «49 точек» (VII): даны 49 точек; требуется провести через эти точки, не отрывая карандаша от бумаги, 12 прямых линий.

Легко заметить, что серия подобных задач может быть продолжена беспредельно. При этом необходимо руководствоваться следующей закономерностью: количество точек должно соответствовать квадратам натурального ряда чисел; количество ли-

⁴ Требование «возвратиться в исходную точку» необходимо лишь для задачи «4 точки». Для всех других задач оно излишне.

230

ний, которыми необходимо соединить точки, должно возрастать на две, соответственно каждому квадрату. Во всех случаях это количество линий будет составлять предел; меньшим числом, не нарушая требований условия задачи, соединить точки невозможно.

Нужное число линий соответственно избранному количеству точек легко определить, пользуясь уравнением

где у — количество линий, а х — количество точек, нарастающее как квадраты натурального ряда чисел (9, 16, 25, 36, 49, 64,81, 100, 122, 144 и т.д.).

Соответственно данной закономерности мы могли использовать задачи: «64 точки» (VIII); «81 точка» (IX); «100 точек» (X); «122 точки» (XI); «144 точки» (XII) и т. д.

В цедом цикл задач можно было рассматривать как сложную познавательную задачу — проблему. Однако эта проблема давалась испытуемым не сразу (например, «144 точки»), а по отдельным задачам — звеньям. Решение первого звена («3 точки») раскрывало исходный принцип («выйти за пределы плоскости, ограниченной точками»), пронизывающий весь последующий путь «восхождения».

Взрослым испытуемым одна за другой предъявлялись задачи данного цикла (I, II, III, IV, V, VI, VII и т. д.) до тех пор, пока испытуемый не вскрывал принцип, удовлетворяющий решению любого звена, т. е. пока не решалась вся сложная познавательная задача.

В других сериях опытов наряду с данной методикой использовались разного рода образующие задачи с последующим учетом их эффективности как по линии прямого, так и по линии побочного продукта.

Прежде всего был прослежен общий ход решения задач данного цикла, т. е. последовательное решение сложной познавательной задачи.

Решение задачи «-точки». Наиболее простой в познавательном отношении среди всех прочих задач является задача «3 точки». В этой задаче нахождение решения полностью совпадает с самим решением, поскольку необходимость в какой-либо конкретизации найденного принципа, его уточнения для применения к данным конкретным условиям задачи полностью отсутствует. Эта задача была бы наиболее удачным объектом для изучения интуитивных решений. Однако в этом отношении ей присущ недостаток: принцип выйти за пределы участка плоскости, ограниченного точками, перекрывается более простым приемом — возможностью соединить три точки просто двумя прямыми, не выходя при этом за указанные пределы. Поэтому для образования психологической трудности данная задача нуждается в усложнении условий, выражающемся во введении

231

Т-образной преграды, исключающей эту перекрывающую данный принцип возможность.

Как правило, задача «3 точки» (с Т-образной преградой) решается без помощи специальной образующей задачи. Дело в том, что, действуя согласно дополнительным ориентирам (Т-образная преграда), испытуемый сам строит в данной ситуации образующую задачу, решение которой совпадает с решением выявляющей задачи, а побочный продукт в таких условиях во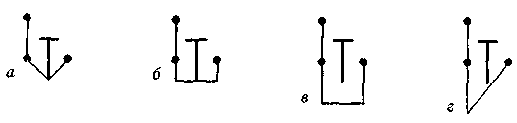



Рис. 22

всех случаях совпадает с прямым продуктом, поскольку, действуя по ориентирам, испытуемый не имеет конкретного замысла плана решения, а ориентиры как бы ведут его к нему.

Наиболее часто решение задачи «3 точки» испытуемыми строится по схеме, изображенной на рис. 22. Вначале используются не две данные линии, а три (одна прямая превращается в ломаную). Концы этой линии соединяются с окончанием преграды (рис. 22, а), затем чертеж принимает вид, изображенный на рис. 22, б, в, и лишь далее, после многих других попыток, находится решение (рис. 22,г).

Если использовать эту задачу в образующей функции и предварить ею «4 точки», то последняя легко решается, даже если образующая задача «3 точки» дается без стимулирующей, т. е. при прямом порядке предъявления. Отсюда следует, что данная задача («3 точки») встает по отношению к задаче «4 точки» в иное отношение, чем все ранее встречавшиеся образующие задачи. Дело в том, что, как мы уже отмечали, конечный маршрут руки испытуемого, являющийся ключом к решению «4 точек», выступает здесь уже не как побочный, а как прямой продукт действия: сама задача «3 точки» выполняет и стимулирующую и образующую функции.

В результате решения задачи «3 точки» испытуемый вырабатывает исходный принцип решения всего цикла задач с нарастающим количеством точек.

Особенностью задачи «3 точки», как мы уже отмечали, является то, что в ее условие вводится дополнение — преграда, конец которой рассматривается испытуемым как дополнительная точка, с которой он и соединяет первую проведенную им линию (по принципу элементарного соединения). Далее, анализируя задачу с помощью элементарного приема (соединение точек по кратчайшему расстоянию), испытуемый приходит к тому, что выравнивает ломаную линию.

232

После этого поиск организуется за внутренними пределами фигуры, образуемой точками, что дает возможность перенести наличный способ «элементарного объединения» в несколько иные условия. Наконец испытуемый, выделив первый угол как еще одну точку, связывает его с третьей и в результате достигает решения.

Опыт показывает, что если испытуемый не знает принципа решения, то задачу типа «4 точек» он может решить лишь в

Рис. 23

том случае, если имеются ориентиры, лежащие вне фигуры, образуемой прямым соединением точек, в зоне которых испытуемый должен действовать. В данном случае, т. е. когда испытуемый решает задачу «3 точки», наличие преграды, требование обойти преграду приводят к необходимости вырваться за пределы фигуры, образуемой точками, причем удачная попытка закрепляется. Таким образом, вырабатывается способ действия, который затем может быть перенесен на решение задачи «4 точки».

Роль особенностей взаимодействия субъекта с объектом, обусловливающих возможность выработки нового способа действия, отчетливо выступает в том случае, если сравнить задачу «3 точки» с другой, внешне совершенно аналогичной: требуется соединить четыре точки, расположенные, как это изображено на рис. 23, двумя связанными прямыми. В результате этого упражнения никогда нельзя добиться непосредственной выработки способа, при помощи которого испытуемый смог бы решить задачу «4 точки».

Итак, действуя по ориентирам путем «элементарного объединения» в ситуации, детерминирующей особое содержание взаимодействия субъекта с объектом, испытуемый вырабатывает способ действия, как бы впитывающий в себя содержание ситуации, в которой он вырабатывается.

В дальнейших опытах этой серии испытуемого, решившего задачу «3 точки», обращали к следующей задаче — к «4 точкам». Особенности решения этой задачи-звена нами уже неоднократно описывались. Добавим лишь одно: обращаясь к задаче «4 точки», после решения «3 точек» испытуемый почти немедленно находил верное решение, поскольку реализация принципа не составляла в данном случае особого затруднения.

После решения «4 точек» испытуемый обращался к следующей задаче-звену цикла — к «9 точкам».



233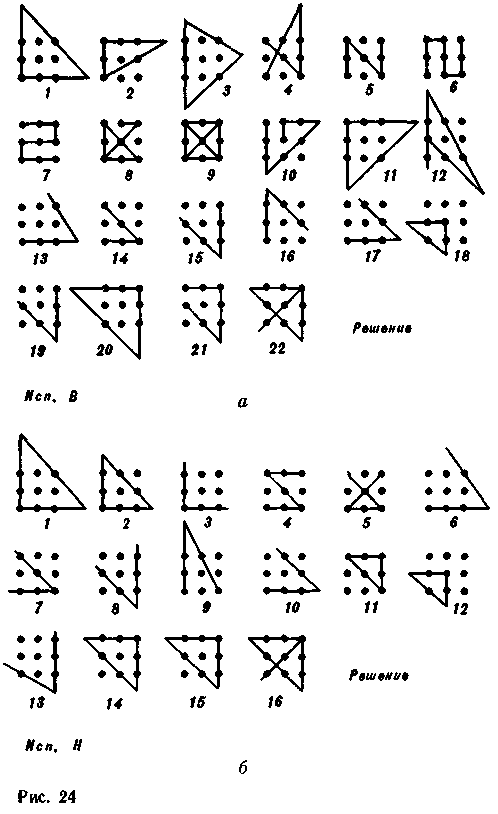



Решение задачи «9 точек». Приведем протоколы решения этой задачи двумя испытуемыми (рис. 24, а, б).

Как видно из протокола, первый испытуемый (В.) нашел решение задачи на 22-й попытке, а испытуемый Н. — на 16-й.

Испытуемым, решившим задачу «9 точек», ставилась задача «16 точек» (в дальнейшем мы будем приводить протоколы решений последующих задач теми же самыми испытуемым) (рис. 25,а,б).

В задаче «16 точек» первый испытуемый (В.) достиг решения на 18-й попытке: второй (Н.) — на 12-й.