Контроль качества в строительстве. Институт сферы обслуживания и предпринимательства (филиал) федеральное государственное бюджетное

• Название: Институт сферы обслуживания и предпринимательства (филиал) федеральное государственное бюджетное
• Анкор: Контроль качества в строительстве
• Дата: 30.05.2022
• Размер: 150.92 Kb.
• Имя файла: Kontroly_kachestva_v_stroitelystve(1).docx
• Тип: Методические указания; #557849
• страница: 8 из 10

Анализ и выводы

Проанализировать полученные результаты. Для выполненных серий испы- таний произвести оценку изменчивости результатов. По результатам обработ- ки результатов сделать выводы о точности полученного значения величины.

Практическая работа №5

Определение массы тела

методом прямых и косвенных измерений

Теоретическое обоснование

При косвенных измерениях искомое значение величины находят расче- том на основе измерения других величин, связанных с измеряемой величи- ной известной зависимостью

  (a_i,..., a_m).

(11)

Результатом косвенного измерения является оценка величины А, ко- торую находят подстановкой в формулу оценок аргументов а_i.

Поскольку каждый из аргументов а, измеряется с некоторой погреш- ностью, то задача оценивания погрешности результата сводится к сум- мированию погрешностей измерения аргументов. Однако особенность кос- венных измерений состоит в том, что вклад отдельных погрешностей изме- рения аргументов в погрешность результата зависит от вида функции (11).

Для оценки погрешностей существенно разделение косвенных изме- рений на линейные и нелинейные косвенные измерения. При линейных кос-венныхизмеренияхуравнение измерений имеет вид:

m

A _b_ia_i,

i1

где b_i– постоянные коэффициенты при аргументах а_i.

(12)

Любые другие функциональные зависимости (11) относятся к не- линейным косвенным измерениям.

Результат линейного косвенного измерения вычисляют по формуле (12), подставляя в нее измеренные значения аргументов.

Погрешности измерения аргументов могут быть заданы своими гра-

ницами

 _ai, либо доверительными границами

a(P)_i, с доверительными ве-

роятностями Р_i.

При малом числе аргументов (меньше пяти) простая оценка погреш-

ности результата Aполучается суммированием предельных погрешностей

(без учета знака), т.е. подстановкой границ

a₁ , a₂ ,

... ,

a_m

в выражение

A a₁  a₂  ...  a_m. (13)

Однако эта оценка является излишне завышенной, поскольку такое суммирование фактически означает, что погрешности измерения всех аргу- ментов одновременно имеют максимальное значение и совпадают по знаку. Вероятность такого совпадения практически равна нулю. Для нахождения более реалистичной оценки переходят к статистическому суммированию по- грешностей аргументов. Полагая, что в заданных границах погрешности ар- гументов распределены равномерно, доверительные границы  (Р) погреш- ности результата измерения рассчитывают по формуле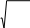

m

P  k

_b² a² ,

(14)

i i

i1

Если погрешности измерения аргументов заданы доверительными гра- ницами с одинаковыми доверительными вероятностями, то полагая распре- деление этих погрешностей нормальным, доверительные границы результата находят по формуле

P 

_b² aP² .

(15)

m
i i

i1

При различных доверительных вероятностях погрешностей аргументов их необходимо привести к одному и тому же значению Р.

Нелинейные косвенные измерения характеризуются тем, что результаты измерений аргументов подвергаются функциональным преобразованиям. Но, как показано в теории вероятностей, любые, даже простейшие функциональ- ные преобразования случайных величин, приводят к изменению законов их распределения.

При сложной функции (11) и в особенности если это функция не- скольких аргументов, отыскание закона распределения погрешности резуль- тата связано со значительными математическими трудностями. Поэтому при нелинейных косвенных измерениях приходится отказываться от использова- ния интервальных оценок погрешности результата, ограничиваясь прибли- женной верхней оценкой ее границ. В основе приближенного оценивания по- грешности нелинейных косвенных измерений лежит линеаризация функции

(11) и дальнейшая обработка результатов, как при линейных измерениях. Запишем выражение для полного дифференциала функции А:

dA

дА_da

• 
  ^дАda
  

 ... 

^дАda.

(16)

1
дА₁

дА₂

дА_m

m

2
По определению полный дифференциал функции – это приращение функции, вызванное малыми приращениями ее аргументов.

Учитывая, что погрешности измерения аргументов всегда являются ма- лыми величинами по сравнению с номинальными значениями аргументов, мож- но заменить в (16) дифференциалы аргументов dа_i, на погрешности измерений  а_i, а дифференциал функции dAна погрешность результата измерения  :

A

дА_a

• 
  ^дАa
  

 ... 

^дАa.

(17)

1
дА₁

дА₂

дА_m

m

2
Полагая, как и прежде, что распределения погрешностей аргументов подчиняются равномерному закону, при числе слагаемых m < 5 границы по- грешности результата можно определить по формуле (13). В том случае, ко- гда погрешности аргументов заданы их доверительными границами, оценку погрешности результата измерения вычисляют по (15). В обеих случаях роль

коэффициентов b₁,b₂,…,b_m выполняют частные производные

дА_.

дА_i

Применив формулу (17), получим несколько простых правил оце- нивания погрешности результата косвенного измерения.

Правило1.Погрешности в суммах и разностях. Если a₁и а₂измерены с по-

грешностями

^a1 и

a₂

и измеренные значения используются для вычисле-

ния суммы или разности

А а₁  а₂ , то суммируются абсолютные погрешности

(без учета знака):

  a₁  a₂.

Правило2.Погрешности в произведениях и частных. Если измеренные зна-

чения а₁, и а₂ используются для вычисления

^{А а1  а2} или А = а₁/а₂, то сумми-

руются относительные погрешности ^{A a}₁ ^{ a}₂ , где a a/ a.

Правило3.Измеренная величина умножается на точное число. Если аис-

пользуется для вычисления произведения грешности, то  А= |В| а.

^{А В а}, в котором Вне имеет по-

Правило4.Возведение в степень. Если аиспользуется для вычисления сте- пени А = аⁿ, то ^{А nа}.

Правило5.Погрешность в произвольной функции одной переменной. Если а

используется для вычисления функции А(а), то ^{A dAa.}

da

Вывод этих правил не приводится и может быть легко сделан само- стоятельно. Использование правил позволяет получить не слишком завы- шенную оценку предельной погрешности результата нелинейного косвен- ного измерения при не слишком большом числе аргументов (m < 5).

В данной работе учащиеся на практике знакомятся с методами измере- ния физических величин. Различают прямыеи косвенныеизмерения.

Прямое измерение – нахождение числового значения искомой физиче- ской величины непосредственно средствами измерения.

Косвенное измерение – нахождение числового значения физической ве- личины по формуле, связывающей ее с другими физическими величинами. Среди них могут быть: физические величины, полученные в результате пря- мых измерений, характеристики установки, справочные и табличные данные, универсальные постоянные. Погрешность косвенно измеряемой величины зависит от погрешностей всех величин, входящих в расчетную формулу.

Точность измерения определяется близостью действительного значе- ния физической величины к истинному. Отклонение результата измерения от истинного значения называется погрешностью. Качество измерений характе- ризуют абсолютнойи относительной погрешностью.

Абсолютная погрешность при однократном прямом измерении равна приборной погрешности. Выражается абсолютная погрешность в единицах измеряемой величины.

Результат однократного прямого измерения принято записывать в виде:

а = а_изм ± Δ а.

Относительная погрешность при однократном прямом измерении – безразмерная физическая величина, равная: ε = Δ а / а_изм.
Цель работы – на практике знакомится с методами измерения физиче- ских величин.

Основная задача – определить массу тела прямым и косвенным мето- дом измерения, научиться рассчитывать абсолютную и относительную по- грешность для данных видов измерений.

Задание – отобрать необходимые приборы, выполнить измерения, вы- числить погрешности прямых и косвенных измерений, представить результа- ты измерений в виде таблицы, интерпретировать результаты эксперимента, сделать выводы и запись конечного результата измерений.

Приборы и оборудование, средства измерения: деревянный брусок, металлический шар, резиновая игрушка, пластмассовый кубик, учебные ве- сы, штангенциркуль, линейка измерительная, мензурка с водой, набор гирь Г4 – 211 для лабораторных работ.