Контроль качества в строительстве. Институт сферы обслуживания и предпринимательства (филиал) федеральное государственное бюджетное

• Название: Институт сферы обслуживания и предпринимательства (филиал) федеральное государственное бюджетное
• Анкор: Контроль качества в строительстве
• Дата: 30.05.2022
• Размер: 150.92 Kb.
• Имя файла: Kontroly_kachestva_v_stroitelystve(1).docx
• Тип: Методические указания; #557849
• страница: 7 из 10

Порядок выполнения работы.

1. 
   Песок насыпать совком в предварительно взвешенный мерный ци- линдр с высоты 10 см от верхнего края до образования над верхом цилиндра конуса. Конус без уплотнения песка снимают вровень с краями сосуда ме- таллической линейкой, после чего сосуд с песком взвешивают. Записать ре- зультаты в таблицу 5.
   
2. 
   Песок насыпают совком в предварительно взвешенный мерный ци- линдр через коническую воронку до образования над верхом цилиндра кону- са. Конус без уплотнения песка снимают вровень с краями сосуда металличе- ской линейкой, после чего сосуд с песком взвешивают. Записать результаты в таблицу 11.
   
3. 
   Определить насыпную плотность песка по формуле (2). Записать ре- зультаты в таблицу 11.
   

Таблица 11

№ измерения	Масса емкости, кг		Объем емкости, м3	Насыпная плотность, кг/м3	Погрешность измерения
	с песком	без песка
с воронкой
1
2
без воронки
1
2

Анализ и выводы.

Проанализировать полученные результаты измерений.

Практическая работа №4

Обработка результатов измерений

Теоретическое обоснование

При определении какого-либо показателя свойства часто приходится сталкиваться с тем, что значения, получаемые при измерении этого показателя неодинаковы. В зависимости от характера проявления, причин возникновения и возможностей устранения различают систематическую и случайную состав- ляющие погрешности измерений, а также грубые погрешности (промахи).

Систематическая составляющая остается постоянной или закономер- но изменяется при повторных измерениях одного и того же параметра.

Случайная составляющая изменяется при повторных измерениях одно- го и того же параметра случайным образом.

Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности СИ или резких изменений условий измерений. Как правило, грубые погрешности выявляются в результате обработки результа- тов измерений с помощью специальных критериев.

Случайная и систематическая составляющие погрешности измерения проявляются одновременно. Значение случайной погрешности заранее неиз- вестно, оно возникает из-за множества неуточненных факторов.

Случайные погрешности нельзя исключить полностью, но их влияние

может быть уменьшено путем обработки результатов измерений. Для этого должны быть известны вероятностные и статистические характеристики (за- кон распределения, закон математического ожидания, среднеквадратическое отклонение, доверительная вероятность и доверительный интервал).

Прямые равноточные измерения

Задача обработки результатов измерений заключается в нахождении приближенного значения или оценки измеряемой величины X и указания ее среднего квадратического отклонения. Если измерения проводились по од- ной и той же методике средствами измерений одинаковой точности при по- стоянных внешних условиях, то такие измерения называются равноточными.

Для них справедливо равенство  ²   ²  ...  ²  const

для всех членов ряда.

1 2 n

При таких измерениях, дающих уже упомянутый ряд измеренных зна- чений величины х₁,x₂,...,х_п,находят:

1. 
   среднее арифметическое значение x.
   

n

Среднее арифметическое значение — статистическая характеристика, описывающая одним числом результаты некоторого ряда измерений. Сред- нее арифметическое значение xвычисляют по формуле

_ x_i

x^i1 (3)

n

где х_i–результат i-го измерений; п–число измерений.

Среднее арифметическое дает представление о среднем значении изме- ряемой величины, но ее изменчивости, т. е. пределов колебания (варьирова- ния) этой величины, не отражает.

2. 
   среднее квадратическое отклонение.
   

Среднее квадратичное отклонение σ_xслужит характеристикой средней изменчивости изучаемой величины. Его выражают в тех же единицах, что и среднее арифметическое значение и вычисляют по формуле


_x 

, (4)

где

_x


n

i
i1

• 
  x2 – сумма квадратов отклонений всех измерений от сред-
  

него арифметического.

Знак плюс или минус в формуле показывает, что отклонение может быть как в одну, так и в другую сторону от среднего арифметического.

Квадрат среднего квадратичного отклонения σ_x²называется дисперсией.Среднее квадратичное отклонение – одна из наиболее важных стати- стических характеристик. Однако его абсолютное значение не позволяет сравнить степень изменчивости изучаемого свойства у нескольких групп ма-

териалов. Показатель относительной изменчивости v=(σ_x/x)·100, (%), на- зываемый коэффициентомвариации, позволяет делать такие выводы.

3. 
   
   x
   среднее квадратическое отклонение 
   

среднего арифметического

 ^ . (5)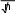
x

x
Среднее арифметическое из ряда измерений всегда имеет меньшую по- грешность, чем погрешность каждого определенного измерения. Это отража- ет и формула (5), определяющая фундаментальный закон теории погрешно- стей. Из него следует, что если необходимо повысить точность результата (при исключенной систематической погрешности) в 2 раза, то число измере- ний нужно увеличить в 4 раза; если требуется увеличить точность в 3 раза, то число измерений увеличивают в 9 раз и т. д.

Нужно четко разграничивать применение σ_xи  _x: величина  _x

исполь-

зуется при оценке погрешностей окончательного результата, а σ_x– при оцен- ке погрешности метода измерения.

4. 
   доверительный интервал по числу измерений nи доверительной ве- роятности рдля найденного значения xспомощью таблиц Стъюдента:
   

p x
  t  ^{, (6)}

где t_p– коэффициент доверительной вероятности, определяемый по таблице 12.

Таблица 12

Коэффициент распределения Стьюдента t_p

При доверительной вероятности р							При доверительной вероятности р
n	0,90	0,95	0,98	0,99	0.999	n		0,90	0,95	0,98	0,99	0,999
2	6,31	12,71	31,82	63,68	636,62	12		1,80	2,20	2,72	3,11	4,44
3	2,92	4,30	6,97	9,93	31,60	13		1,78	2,18	2,68	3,06	4,32
4	2,35	3,18	4,54	5,84	12,92	14		1,77	2,16	2,65	3,01	4,22
5	2,13	2,78	3,75	4,60	8,61	15		1,76	2,15	2,62	2,98	4,14
6	2,02	2,57	3,37	4,06	6,87	16		1,75	2,13	2,60	2,95	4,07
7	1,94	2,45	3,14	3,71	5,96	17		1,75	2,12	2,58	2,92	4,02
8	1,90	2,37	3,00	3,50	5,41	18		1,74	2,11	2,57	2,90	3,97
9	1,86	2,31	2,90	3,36	5,04	19		1,73	2,10	2,55	2,88	3,92
10	1,83	2,26	2,82	3,25	4,78	20		1,73	2,09	2,54	2,86	3,88
11	1,81	2,23	2,76	3,17	4,59	∞		1,65	1,96	2,33	2,58	3,29

Прямые неравноточные измерения

В некоторых случаях одну и ту же величину необходимо измерить раз- личными методами и средствами измерений. Тогда точность и, соответственно,

^{дисперсии нескольких полученных значений будут различны}  ²   ²  ...  ^{2 .}

1 2 n

Объединение результатов таких измерений заключается в нахождении так называемого среднего взвешенного или весового среднего. Последнее яв- ляется той оценкой искомого значения величины, которое при заданных ре-

зультатах измерений x_l,x₂,х₃,...,х_nи их дисперсиях  ² , ² ,..., ² , имеет мини-

мальную дисперсию.

Средневзвешенное значение


n
_ p_i x_i

1 2 n

x_p^{определяют по формуле:}
n

n

p
x^{i1 или}

_ p_i

x_p __i

i1

 x_i

, (7)

i1

в которой p_iопределяет «вес» i-ro измерения.

Вес измерения характеризует степень доверия к соответствующим ря- дам наблюдений и может быть вычислен по формуле:

^{p 1} или

_{ } 1/  ²

(8)

i
ⁱ _ 2 ^{i n} ₂

ⁱ_ 1/ _i

i1

Значение среднего квадратического отклонения находят по формуле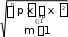



_p (9)

где m– число групп измерений, а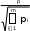





_xp 

(10)

Оценка грубых погрешностей

При обработке экспериментальных данных в некоторых случаях отдель- ные результаты измерений имеют значительно большее отклонение от средне- го, чем остальные. В подобных случаях прежде всего проверяют, не допущена ли ошибка в процессе эксперимента. Источником грубых погрешностей не- редко бывают ошибки, допущенные оператором во время измерений.

Вопрос о том, содержит ли результат наблюдений грубую погреш- ность, решается общими методами проверки статистических гипотез. Прове- ряемая гипотеза состоит в утверждении, что результат наблюдения x_iне со- держит грубой погрешности, т. е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытают- ся опровергнуть выдвинутую гипотезу. Если это удается, то результат на- блюдений рассматривают, как содержащий грубую погрешность, если нет – то не исключают. Существует ряд критериев для оценки промахов.

Критерий 3σ. В этом случае считается, что результат, возникающий с вероятностью Р≤ 0,003, малореален и его можно квалифицировать промахом,

т. е. сомнительный результат x_i, отбрасывается, если

x x_i

• 
  3 ^.
  

Величины xи σвычисляют без учета х_iДанный критерий надежен при числе измерений n>20,...,50.

Если п <20, целесообразно применять критерийРомановского.

При этом вычисляют отношение

_{ } и полученное значение βсрав-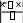

нивают с теоретическим β_т– при выбираемом уровне значимости α=(1-P)·100%

по таблице 13.

Таблица 13

Уровень значимости β_т =f(n)

Уровень зна- чимости α, %	Число измерений
	n=4	n=6	n=8	n=10	n=12	n=15	n=20
1	1,73	2,16	2,43	2,62	2,75	2,90	3,08
2	1,72	2,13	2,37	2,54	2,66	2,80	2,96
5	1,71	2,10	2,27	2,41	2,52	2,64	2,78
10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Если окажется, что β < β_тто в результатах отсутствует грубая погреш- ность, в противном случае β ≥ β_трезультат содержит грубую погрешность и его из обработки исключают.

Цель работы – ознакомиться с методами обработки результатов изме- рений и приобрести навыки определения значения измеряемой величины.

Основная задача – произвести математическую обработку результа- тов испытаний.

Задание – найти приближенное значение измеряемой величины и ее среднее квадратическое отклонение, определить изменчивость изучаемого свойства у нескольких групп материалов.

Приборы и оборудование – пресс гидравлический ПГ-5; индикатор часового типа ИЧ-10; сферический индентор; образец в виде прямоугольной призмы сечением 50×50 мм и длиной 50 мм; инженерный калькулятор.

Порядок выполнения работы.

1. 
   Произвести определение твердости древесины статическим методом (ГОСТ 16483.17-81). Испытания производятся по одной поверхности образца (торцовой, радиальной или тангенциальной). Испытания проводят три брига- ды студентов. Количество испытаний в каждой серии не менее 10. Результа- ты занести в таблицу 14.
   
2. 
   Произвести обработку равноточных результатов измерений. Для каждой серии испытаний вычисляют среднее арифметическое значение xпо
   


формуле (3) и среднее квадратическое отклонение σ_xи _xпо формулам (4)

и (5). Записать результаты в таблицу 14. Используя критерий Романовского исключают промахи. При заданном значении доверительной вероятности р=0,95 и числе измерений по таблице 12 определяют коэффициент Стъюден- та и находят границы доверительного интервала для случайной погрешно- сти. Окончательный результат записать в виде x= x .

3. 
   Произвести обработку неравноточных результатов измерений. Для трех серий испытаний найти средневзвешенное значение и произвести оцен-
   

ку точности. Записать результаты в таблицу 15.
Таблица 14

Результаты обработки равноточных измерений

№ серии	xi, МПа	x , МПа	xi x	x x2 i	σx, МПа	β	 x	Δ	x, МПа
1
2
3

Таблица 15

Результаты обработки неравноточных измерений

xi, МПа	Δ	pi	xp, МПа	xi xp	x x2 i p	p x x2 i i p	 р	 х р