Ннагашащща. ПЗ№ 3 Опред. инт Word. Интегрирование функций. Определённый интеграл с курсантами 1 курса по специальности 31. 05. 01 Лечебное дело
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
ВОЕННО-МЕДИЦИНСКАЯ АКАДЕМИЯимени С.М. Кирова Кафедра биологической и медицинской физикиЗАДАНИЕ для проведения практического занятия № 3по дисциплине «Физика, математика» на тему: Интегрирование функций. Определённый интеграл с курсантами 1 курса по специальности 31.05.01 «Лечебное дело» При подготовке к занятию по теме ИНТЕГРИРОВАНИЕ ФУНКЦИЙ. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ курсанты должны самостоятельно изучить учебный материал по следующим учебным вопросам: Определённый интеграла. Свойства определенного интеграла. Правила нахождения определённых интегралов. Формула Ньютона-Лейбница. Геометрический смысл определённого интеграла. Физический смысл определенного интеграла. Литература: Обязательная: а) Электронный учебник. Поцелуев К.А., Новикова Н.Г. Краткое введение в математику: учебное пособие. – СПб.: ВМедА, 2016. Гл. 1,2.– 90 с. б) Математика. Под ред. Буга С.В. Базовый электронный учебник. – Михайловская военная артиллерийская академия, 2017 в) Лекционные записи. План выполнения задания Ознакомиться с теоретическим материалом и внести (при необходимости) дополнения в конспект лекций; Изучить обучающие задачи; Решить задания с вариантами ответов (в тетрадях по практическим занятиям); Решить соответствующие варианты самостоятельных работ (в тетрадях по практическим занятиям). Номер варианта соответствует номеру курсанта в группе. Теоретическая часть 1. Вычисление площади криволинейной трапеции
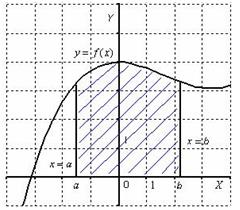
Учитывая, что площадь фигуры, состоящей из нескольких непересекающихся фигур, равна сумме площадей этих фигур, получим 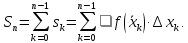 (1) (1)Эта сумма является приближением для искомой площади, причём чем 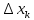 меньше, тем это приближение точнее, следовательно меньше, тем это приближение точнее, следовательноS= площадь aABb= 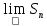 , ,где переход к пределу происходит при условии 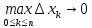 2. Понятие определённого интеграла Определённым интегралом называется предел, к которому стремится интегральная сумма (1) при стремлении к нулю длины наибольшего частичного интервала 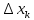 . .В общем случае, такой предел называется определённым интегралом от функции f(x) в пределах от a до b и обозначается 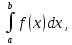 где 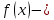 подинтегральная функция; подинтегральная функция; 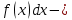 подинтегральное выражение; подинтегральное выражение;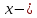 переменная интегрирования; a – нижний предел интеграла; b – верхний предел интеграла; переменная интегрирования; a – нижний предел интеграла; b – верхний предел интеграла; 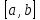 – промежуток интегрирования. – промежуток интегрирования.Геометрический смысл определённого интеграла. Определённый интеграл от неотрицательной функции численно равен площади криволинейной трапеции. Важно понимать, что определенный интеграл, в отличие от неопределенного интеграла, является числом, а не функцией. Физический смысл определённого интеграла Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и зависящей от x: F = F(x), где х — абсцисса движущейся точки М, т.е. y=F (x). На элементарном участке пути 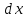 работа силы работа силы 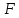 равна, по определению, равна, по определению, 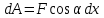 , где , где 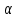 – угол между направлением силы и направлением движения на данном элементарном участке пути – угол между направлением силы и направлением движения на данном элементарном участке пути 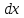 . Работа на конечном пути равна сумме элементарных работ, совершаемых на элементарных участках пути . Работа на конечном пути равна сумме элементарных работ, совершаемых на элементарных участках пути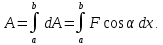 Таким образом, работа переменной силы F (x), действующей на отрезке 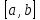 , равна определённому интегралу от величины силы F(x), взятому по отрезку , равна определённому интегралу от величины силы F(x), взятому по отрезку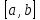 . .Физический смысл определённого интеграла – это работа переменной силы.F = F(x), Свойства определённого интеграла 1. Интеграл от a до b от суммы двух функций f(x) и g(x) равен сумме интегралов от этих функций. 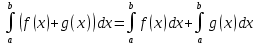 2. Постоянный множитель можно вынести за знак определенного интеграла. 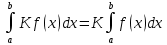 3. Если нижний и верхний пределы интегрирования поменять местами, то знак интеграла изменится на противоположный. 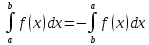 4. Если точка С лежит на отрезке [a; b], то 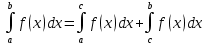 Формула Ньютона-Лейбница Простым и удобным методом вычисления определённого интеграла  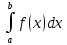 от непрерывной функции является формула Ньютона-Лейбница: 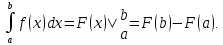 Применяется этот метод во всех случаях, когда может быть найдена первообразная функцияF(x) для подинтегральной функции f(x). Метод вычисления определённого интеграла: 1) Находим первообразную (см. материал практического занятия №2), 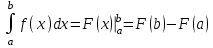 2) Применяем формулу Ньютона-Лейбница 2) Применяем формулу Ньютона-ЛейбницаДля нахождения первообразной применяют таблицу основных интегралов Таблица основных интегралов 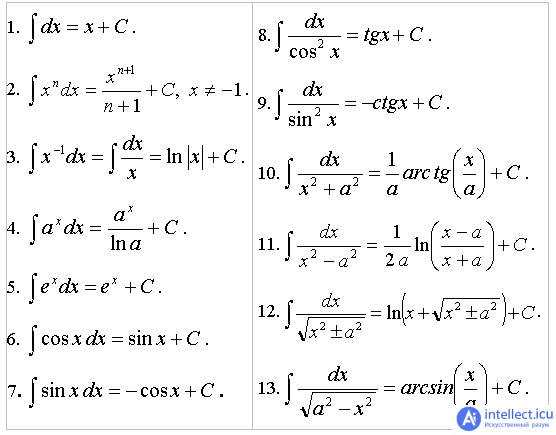 Задачи обучающего типа № 1 Рассмотрим примеры вычисление простейших определённых интегралов при помощи таблицы интегралов и формулы Ньютона-Лейбница. Пример 1. 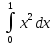 Итак, 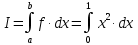 Решение: 1) Применим формулу 2 из таблицы интегралов. В данном случае степень 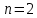 . Тогда первообразная будет равна . Тогда первообразная будет равна 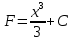 2) Применим формулу Ньютона- Лейбница 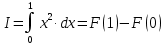 . .3) Подставляем вместо 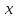 в полученную для первообразной формулу сначала 1, а затем 0: в полученную для первообразной формулу сначала 1, а затем 0: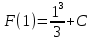 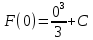 Вычитаем: 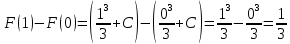 Итак, 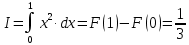 . .Ответ 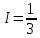 Важно обратить внимание на то, что константа 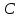 сократилась. Это означает, что если мы вычисляем определенный интеграл, то константу С можно для краткости не писать – она все равно сократится. сократилась. Это означает, что если мы вычисляем определенный интеграл, то константу С можно для краткости не писать – она все равно сократится.Пример 2 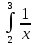 dx dxИтак, 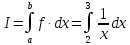 Решение: 1) Применим формулу 3 из таблицы интегралов. В данном случае степень 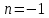 . Тогда первообразная будет равна . Тогда первообразная будет равна 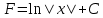 2) Применим формулу Ньютона- Лейбница 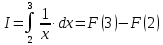 3) Подставляем вместо 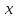 в полученную для первообразной формулу сначала 3, а затем 2: в полученную для первообразной формулу сначала 3, а затем 2: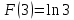 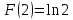 Вычитаем: 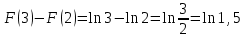 Ответ 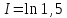 Пример 3. 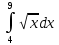 Итак, 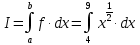 Решение: 1) Применим формулу 2 из таблицы интегралов. В данном случае степень 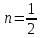 . Тогда первообразная будет равна . Тогда первообразная будет равна 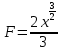 2) Применим формулу Ньютона- Лейбница 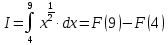 . .3) Подставляем вместо 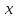 в полученную формулу сначала 9, а затем 4: в полученную формулу сначала 9, а затем 4: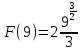 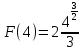 Вычитаем: 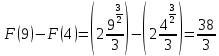 Итак, 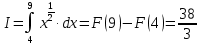 . .Если метод вычисления определённого интеграла вам понятен, то можно кратко решение записать в виде: 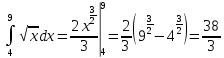 Ответ 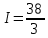 Пример 4. 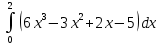 Итак, 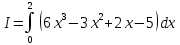 Решение: Внутренняя часть интеграла состоит из нескольких слагаемых. Поэтому будем вычислить определённый интеграл от каждого слагаемого. Множитель - это число и его можно вынести за знак интеграла. Тогда получим 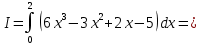 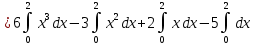 3. Применим формулу 2 из таблицы интегралов для определения первообразной каждого из четырёх интегралов. 4. Применим формулу Ньютона- Лейбница для расчёта каждого интеграла 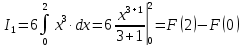 . .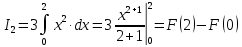 . .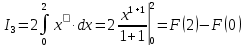 . .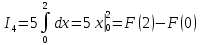 . .Если метод вычисления определённого интеграла вам понятен, то можно кратко решение записать в виде: 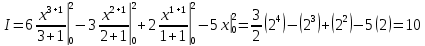 Ответ 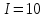 Пример 5. 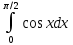 Решение: 1. Применим формулу 6 из таблицы интегралов для определения первообразной 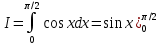 2. Применим формулу Ньютона- Лейбница 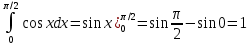 Ответ Ответ 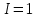 Задачи обучающего типа № 2 Рассмотрим примеры вычисление определённых интегралов при помощи метода замены переменной и формулы Ньютона-Лейбница). Пример 1. 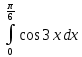 Решение: 1. При вычислении этого интеграла сделаем замену переменной t = 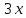 ,следовательно ,следовательно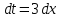 , тогда , тогда 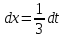 . .Интеграл будет иметь вид: 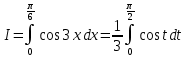 Обратите внимание, что для переменной t, нижний предел остался прежним, а верхний предел изменился: для 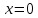 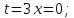 , ,для 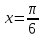 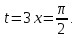 2. Применим формулу 6 из таблицы интегралов и найдём первообразную 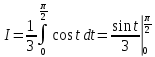 3. Применим формулу Ньютона- Лейбница 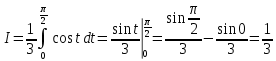 Если метод вычисления определённого интеграла вам понятен, то кратко решение можно записать в виде: 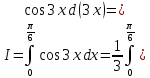 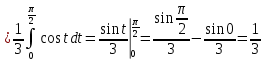 Ответ: 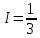 Пример 2. 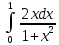 Решение: 1. Преобразуем выражение под интегралом и введём новую переменную 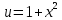 , следовательно , следовательно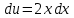 . .Интеграл будет иметь вид: 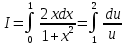 Обратите внимание, что для переменной u, нижний и верхний пределы изменились для 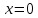 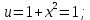 , ,для 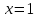 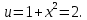 2. По формуле 3 из таблицы интегралов найдём первообразную. 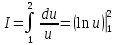 3. Применим формулу Ньютона- Лейбница. 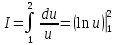 = =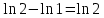 Кратко решение можно записать в виде: 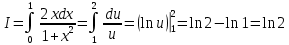 Ответ: 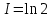 |

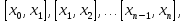 считая что
считая что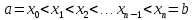
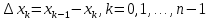
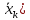 :
: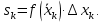
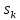 приближённо равняется площади k-ой элементарной криволинейной трапеции с тем же основанием (см. рис.2).
приближённо равняется площади k-ой элементарной криволинейной трапеции с тем же основанием (см. рис.2).