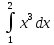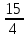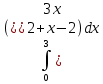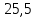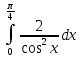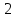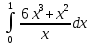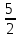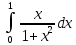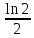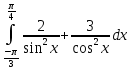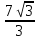Ннагашащща. ПЗ№ 3 Опред. инт Word. Интегрирование функций. Определённый интеграл с курсантами 1 курса по специальности 31. 05. 01 Лечебное дело
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Пример 3. 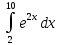 Решение: 1. При вычислении этого интеграла сделаем замену переменной t = 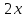 ,следовательно ,следовательно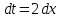 , тогда , тогда 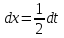 . .Интеграл будет иметь вид: I= 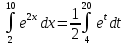 Обратите внимание, что для переменной t, нижний и верхний пределы изменились для 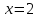 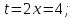 для 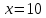 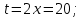 2. По формуле 5 из таблицы интегралов найдём первообразную. I= 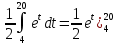 3. Применим формулу Ньютона- Лейбница. I= 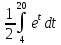 = =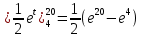 Кратко решение можно записать в виде: I= 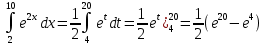 Ответ: 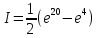 Пример 4. 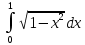 Решение: 1. При вычислении этого интеграла делаем замену переменной 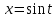 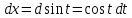 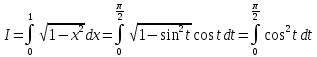 Обратите внимание, что для переменной t, нижний и верхний пределы изменились для 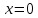 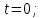 для 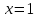 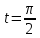 2. Воспользуемся тригонометрическим тождеством 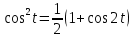 и запишем интеграл в виде суммы двух интегралов: 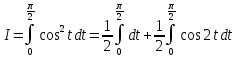 Первый интеграл 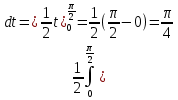 Второй интеграл запишем в виде 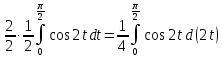 3. По формуле 6 из таблицы интегралов найдём первообразную для второго интеграла 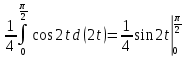 Применим формулу Ньютона- Лейбница. 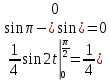 Следовательно 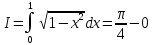 Ответ: 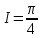 Пример 5. 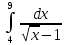 Решение: 1. При вычислении этого интеграла сделаем замену переменной 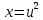 ,следовательно ,следовательно1) 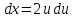 . .Интеграл будет иметь вид: 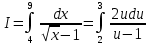 Обратите внимание, что для переменной u, нижний и верхний пределы изменились для 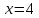 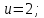 для 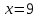 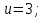 Перепишем интеграл в виде 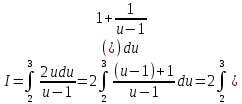 Запишем этот интеграл в виде суммы двух интегралов: 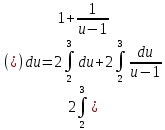 Первый интеграл 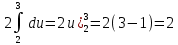 Второй интеграл запишем в виде 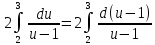 3. По формуле 3 из таблицы интегралов найдём первообразную для второго интеграла 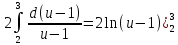 Применим формулу Ньютона- Лейбница. 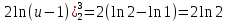 Следовательно 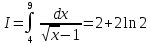 Ответ: 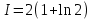 Задачи обучающего типа № 3 (геометрический смысл определенного интеграла) Рассмотрим примеры вычисления площадей плоских фигур с помощью определённого интеграла. Пример 1. Вычислить площадь фигуры, ограниченной параболой 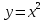 , осью Ox и прямыми , осью Ox и прямымиx= 0 и x= 1. Для наглядности начертим график этой параболы: И 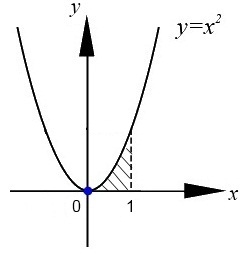 так, так, 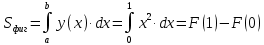 . .Таким образом, чтобы найти эту площадь, достаточно 1) выяснить первообразную от функции 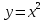 2) посчитать значение этой первообразной 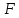 при 1 при 1 и при 0. 3) Вычесть из первого числа второе. Действуем: 1) Из таблицы интегралов находим, что 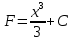 2) Подставляем вместо 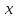 в полученную формулу 1, в полученную формулу 1, а затем 0: 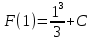 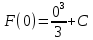 3) Вычитаем и получаем: 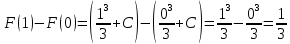 Ответ: 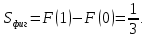 Ещё раз, обратим внимание на то, что константа 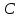 сократилась. сократилась. Пример 2. Вычислить площадь фигуры, ограниченной параболой 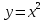 , осью Ox и прямыми , осью Ox и прямымиx= 2 и x= 4. 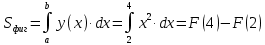 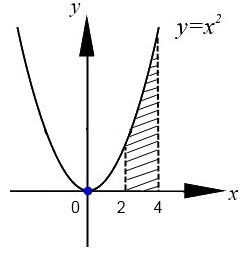 Поскольку исходная функция 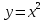 ,то первообразная равна ,то первообразная равна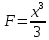 Константу 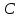 уже не пишем, зная, что она все равно сократится. уже не пишем, зная, что она все равно сократится. 2) Подставляем вместо 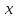 в эту формулу 4, а затем 2: в эту формулу 4, а затем 2: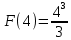 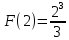 Вычитаем и получаем: 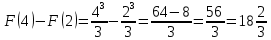 Ответ: 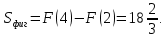 Пример 3. Вычислить площадь фигуры, ограниченной кривой 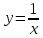 , осью Ox и прямыми , осью Ox и прямымиx= 2 и x= 3 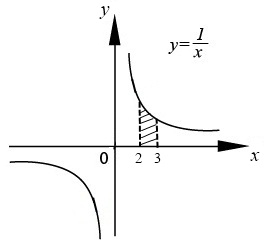 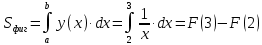 Из таблицы первообразных находим, что 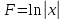 . .Константу 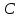 уже не пишем, зная, что она все равно сократится. уже не пишем, зная, что она все равно сократится.Учитывая, что для рассматриваемого диапазона значений 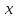 (от 2 до 3) (от 2 до 3) 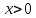 , знак модуля можно убрать. , знак модуля можно убрать.Тогда 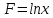 Подставляем вместо 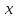 в эту формулу в эту формулу 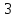 , а затем 2: , а затем 2: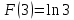 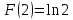 Вычитаем и получаем: 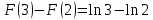 Используя свойство логарифма 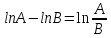 , запишем ответ более компактно: , запишем ответ более компактно: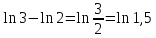 Ответ: 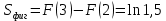 Пример 4. Вычислить площадь фигуры, ограниченной кривой 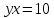 , осью Ox и прямыми x= 1 , осью Ox и прямыми x= 1и x= 2. 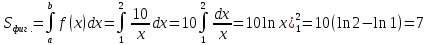 (Здесь ln2 = 0,7) Ответ: 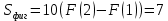 Пример 5. Вычислить площадь фигуры, ограниченной кривыми 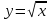 и и 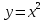 (см. рис.). (см. рис.).
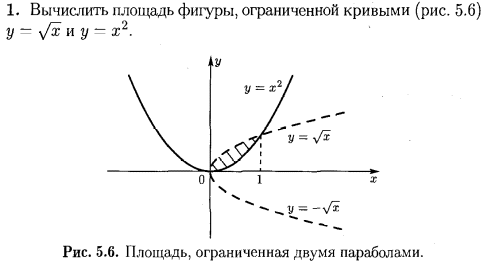 Решение. Находим точки пересечения кривых: 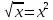 , следовательно , следовательно 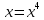 , откуда , откуда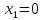 , , 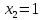 . .По формуле 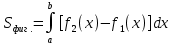 , ,где 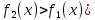 получим получим Задачи обучающего типа № 4 (физический смысл определенного интеграла) Пример 1. Растяжение пружины пропорционально приложенной силе ( 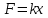 ). Вычислить работу ( ). Вычислить работу (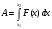 )), произведенную при растяжении пружины от 2 до 2,5 см, если для растяжения пружины на 1 см требуется сила 30 Н. )), произведенную при растяжении пружины от 2 до 2,5 см, если для растяжения пружины на 1 см требуется сила 30 Н.Решение. Подставив данные в формулу закона Гука, получим: 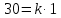 , т.е. коэффициент пропорциональности k=30н/см. Следовательно, сила упругости выражается соотношением F=30x. Найдем работу переменной силы по формуле , т.е. коэффициент пропорциональности k=30н/см. Следовательно, сила упругости выражается соотношением F=30x. Найдем работу переменной силы по формуле 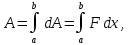 полагая, что а=2; b=2,5: полагая, что а=2; b=2,5: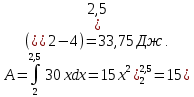 Пример 2. Тело движется прямолинейно. Скорость тела меняется со временем по закону: 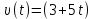 (м/с). Определить путь, пройденный телом, за промежуток времени от 2 с до 3 с. (м/с). Определить путь, пройденный телом, за промежуток времени от 2 с до 3 с.Решение. Поскольку 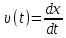 , следовательно , следовательно 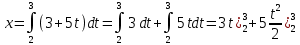 Таким образом, 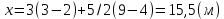 Пример 3. Через участок тела животного проходит импульс тока, который изменяется по закону 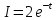 А. Определить заряд, протекающий через тело животного за 0,2 с. А. Определить заряд, протекающий через тело животного за 0,2 с.Решение. Поскольку 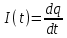 , следовательно , следовательно 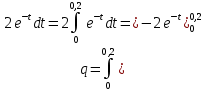 Таким образом, 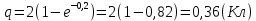 Пример 4. Известно, что после замыкания электрической цепи сила тока меняется по закону 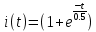 мА. Какое количество электричества ( мА. Какое количество электричества (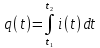 ) протекает через проводник за 1 с? ) протекает через проводник за 1 с?Решение. Поскольку 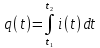 , , следовательно следовательно 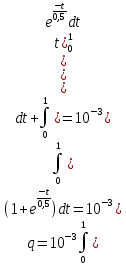 Таким образом, 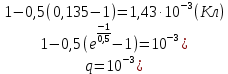 Пример 5. Какая работа совершается при растяжении мышцы на L мм, если известно, что при нагрузке 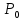 мышца растягивается на мышца растягивается на 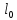 мм? Считать, что сила, необходимая для растяжения мышцы, пропорциональна ее удлинению. мм? Считать, что сила, необходимая для растяжения мышцы, пропорциональна ее удлинению.Пусть 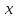 - удлинение мышцы, а - удлинение мышцы, а 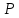 - прикладываемая сила. По условию - прикладываемая сила. По условию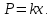 Коэффициент пропорциональности 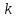 равен по условию равен по условию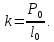 Работа, совершаемая при растяжении мышцы, будет равна 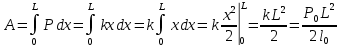 Задания для самостоятельной работы с вариантами ответов
|