8.4. МОДЕЛИРОВАНИЕ ДЕНЕЖНЫХ ПОТОКОВ ПРЕДПРИЯТИЯ.
Движение денежных средств в процессе проведения любых финансовых операций удобно рассматривать как численный ряд, состоящий из распределенных во времени платежей и представляющий собой совокупность целенаправленного движения денег. Он называется денежным потоком. Поток денежных средств – разность между всеми полученными и выплаченными предприятием денежными средствами за определенный период времени. Большинство денежных потоков представляют собой серии периодически равных или произвольных по величине платежей.
Управление денежными потоками включает:
• учет движения денежных средств
• анализ потоков денежных средств
• составление бюджета денежных средств
и охватывает основные аспекты управления деятельности компании.
Основная задача анализа денежных потоков заключается в выявлении причин недостатка (избытка) денежных средств, определении источников их поступлений и направлений использования.
Необходимо составить кассовый бюджет – Сash flow (план движения денежных средств), который является частью финансового плана. Расчет показателей, отражающих изменения в каждом из трех разделов отчета о движении денежных средств, включает определение остатка денежных средств на конец отчетного периода как алгебраической суммы денежных средств на начало периода и изменений за период.
В разделе притока средств от операционной деятельности отражаются такие показатели, как: оплата покупателями продукции, поступления от реализации необоротных активов и т.д. Отток денежных средств по этому виду деятельности вызван выплатой заработной платы, выплатой процентов по займам, оплата поставленной компании продукции, налогообложение и т.д.
Потоки по инвестиционной деятельности вызваны реализацией и покупкой недвижимого имущества, ценных бумаг, предоставления и получения долгосрочных займов и т.д.
Финансовая деятельность состоит из операций с акционерным капиталом, выпуском облигаций, выплатой дивидендов и т.д.
Расчет показателей, отражающих изменения в каждом из трех разделов отчета о движении денежных средств, включает определение остатка денежных средств на конец отчетного периода как алгебраической суммы денежных средств на начало периода и изменений за период.
Финансовые ресурсы, материальную основу которых составляют деньги, имеют временную ценность. Временная ценность финансовых ресурсов может рассматриваться в двух аспектах. Первый аспект связан с покупательной способностью денег. Второй аспект связан с обращением денежных средств как капитала и получением доходов от этого оборота. Деньги как можно быстрее должны делать новые деньги.
Дисконтирование доходов –приведение дохода к моменту вложения капитала.
Дисконтирование дохода применяется для оценки будущих денежных поступлений (прибыль, проценты, дивиденды) с позиции текущего момента. Инвестор, сделав вложение капитала, руководствуется следующими положениями. Во-первых, происходит постоянное обесценение денег; во-вторух, желательно периодическое поступление дохода на капитал, причем в размере не ниже определенного минимума.
Процесс дисконтирования легче всего представить при вычислении дохода по банковским сделкам (кредитование или вкладные операции).
Рассмотрим аппарат финансовых вычислений, широко используемый в финансовой практике и составляющий основу механизма расчетов при совершении кредитных операций, операций на фондовом рынке, при выборе вариантов инвестиционных проектов, а также выплате дивидендов по ценным бумагам, погашению долгосрочных займов.
Если проанализировать основное содержание перечисленных операций, можно отметить одну особенность, а именно: кредиты выдаются на определенный срок, проценты по депозиту увязываются со временем, выплата дивидендов осуществляется за определенный период, инвестиции капитала также связаны с конкретным периодом времени. Следовательно, важнейшее место в финансовых вычислениях занимает фактор времени. Возникает задача разработки адекватного механизма, позволяющего учесть этот фактор, проследить его влияние на финансовые результаты и последствия коммерческих сделок и операций.
Термин “дисконтирование” употребляется в финансовом менеджменте весьма широко. Под ним может пониматься способ нахождения стоимости величины Р на некоторый момент времени при условии, что в будущем при начислении на нее процентов она могла бы составить наращенную сумму S. Величину Р, найденную дисконтированием наращенной величины S, называют современной, или приведенной стоимостью. С помощью дисконтирования в финансовых вычислениях учитывается также фактор времени.
Любая финансовая операция порождает движение денежных средств. Оно может выражаться как в разовом платеже, так и в некоторой их последовательности во времени. В качестве примеров можно привести выплату пенсий, периодическое поступление доходов по инвестициям и т.д.
8.4.1.1. Финансовая математика в моделировании денежного потока
Такую последовательность называют потоком платежейили денежным потоком – cash flow (CF). Отдельный элемент потока – CFn – разность между поступлениями (притоками) денежных средств и их оттоками в какой-то определенный период проведения хозяйственной операции.
Анализ денежных потоков сводится к определению следующих обобщающих параметров:
FVn – будущая стоимость потока за n-периодов;
PVn – современная стоимость потока;
CFt – величина потока платежей за время t;
r – процентная ставка;
n – срок.
Денежные потоки бывают элементарными (single cash flow), в виде серии равных платежей (финанасовая рента) и в виде серии произвольных платежей.
Примером элементарных денежных потоков может служить срочный депозит. То есть такой поток состоит из одной выплаты и последующего поступления (или одного поступления и последующей выплаты – единовременная ссуда).
Потоки можно представить в следующих моделях:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сложные %%
|
|
|
|
|
|
|
Н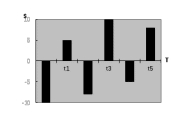 еравномерные доходы и расходы (долгосрочные инвестиции) еравномерные доходы и расходы (долгосрочные инвестиции)
Существуют математический и банковский (коммерческий) методы дисконтирования.
1) Математическое дисконтирование:
При этом используется i – ставка доходности, исчисляемая исходя из наращения первоначальной суммы. При этом:
S – Р = D – доход от сделки (дисконт при вексельной сделке) или:
D = P •n•i.
Для решения этих задач используется формула наращения по простой ставке процентов:
P=S*[1/(1+n*i)],
1
Р = S –––, (1)
1 + n•i
[1/(1+n*i)] - дисконтный множитель
1
где –––– дисконтный множитель, который показывает,
1 + n•i – во сколько раз первоначальная сумма ссуды меньше наращенной суммы;
Р – приведенная величина, или современная стоимость, будущей суммы;
S – наращенная сумма,
n – период получения дохода (в годах)
i – ставка доходности (в долях).
Рассмотрим следующую задачу:
Какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процента по ставке получить наращенную сумму, равную S?
Пример. Вкладчик банка имеет 333,3 тыс. руб. Какую сумму он будет иметь через на 1 год при условии 50% годовых?
Из формулы (1) получаем:
S = P (1 + i •n)
S =333,3 • (1 + 0,5 • 1) = 333,3 • 1,5 = 500 тыс. руб.
Доход вкладчика в этом случае составит:
D = 500 – 333,3 = 166,7 тыс. руб.
В процессе подготовки к подписанию контрактов возникает необходимость определения срока ссуды. Если согласованы основные параметры ссуды (сумма погашения долга S, процентная ставка i, величина ссуды Р), то срок погашения ссуды можно определить по формуле
_ S–P S: P – 1 ,
п = P i = i
где п – срок ссуды в годах.
2) Банковское дисконтирование
Ранее мы рассмотрели наращение суммы, используя процентную ставку i суммы Р. Однако можно использовать и другой подход, когда за базу (100%) принимается сумма погашения долга. В таком случае применяется учетная ставка d. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды по учетной ставке d.
В таких ситуациях наращенная сумма может быть рассчитана по формуле
S = P , (2)
1 – n•d
где n – срок ссуды;
d – учетная ставка (ставка дисконтирования).
Тогда, первоначальная сумма (текущая стоимость) определяется по формуле P = S (1 – n•d).
Пример. 2. Вексель номинальной стоимостью 500 тыс. руб. переуступается банку. Время до погашения векселя 2 месяца. Какую сумму получит векселедержатель если банк принимает его по учетной ставке 50% годовых.?
Решение: Обозначим через S – номинал векселя, то есть эту сумму получить банк у должника. Тогда P – текущая стоимость векселя (цена покупки векселя банком). Теперь переведём месяцы в годы: 2 мес. / 12 мес. = 0,166. Теперь воспользуемся формулой (2), преобразовав её:
P = S (1 -nd)..
От сюда, P = 500 • (1 – 0,166 • 0,5) = 458,5 тыс. руб.
Дисконт (доход банка) в этом случае составит:
D = 500 – 458,5 = 41,5 тыс. руб.
Ставки, применяемые в математическом и банковском учетах, решают практически одни и те же задачи – определение величины Р по заданной F. Это позволяет установить связь между ними, выразив одну ставку через другую. Определим связь между процентной и учетной ставками, для чего запишем формулы расчета современной величины платежа при математическом и банковском видах учета:
Взаимосвязь ставок:
• Процентная ставка (математическое дисконтирование)
it= S–P
P
• Учетная ставка (банковское дисконтирование)
dt=S–P
S
• Соотношение между ставками
it = dt или dt = it ,
1 – dt 1+it
Эти выражения позволяют определить процентную ставку по известной учетной ставке (первое выражение) или учетную ставку по известной процентной ставке. Таким путем мы получаем различные по величине процентные ставки, которые дают одну и ту же дисконтированную величину платежа при фиксированном сроке ссуды. Такие ставки называют эквивалентными. Они используются при сравнении доходности сделок.
1а) Дисконтирование по сложной ставке процента
Расчеты по сложным процентам используются при долгосрочных финансовых операциях. Они основаны на условии, что начисленные за период проценты присоединяются к первоначальной сумме, а определение суммы процентов за следующий период производится исходя из наращенной к началу периода суммы. Таким образом, исходная база начисления в каждом периоде увеличивается на сумму присоединившихся процентов. Процесс наращения происходит здесь с ускорением. Учет по сложным процентам, как и по простым, заключается в определении первоначальной суммы (Р) по заданным наращенной сумме, процентной ставке и периоде сделки по следующей формуле:
1
Р = S –––, (1a)
(1 + i) n
1
где –––– дисконтный множитель
(1 + i) n
Если начисление процентов производится несколько раз в течение года, то расчет современной величины платежа необходимо производить по формуле
S
Р = –––––– ,
(1 + i)nm
m
где т – число случаев начисления процентов в течение года.
Пример. Определим размер вклада, если вкладчик через 5 лет хочет получить 200 млн руб. Банк предлагает производит начисления на внесенную сумму по сложной ставке 20% годовых.
200
Р = ––– = 80,375 млн руб.
(1 + 0,2)5
Если начисление процентов производится ежеквартально, то первоначальная сумма вклада будет меньше.
200
Р = –––––– =75,378 млн руб.
(1 + 0,2 )4 •5
4
2а) При банковском (коммерческом) дисконтировании по сложным учетным ставкам используется формула:
P = S (1 – d)n. (2а)
Пример. Определим величину банковского кредита сроком 5 лет, если всего банк желает получить в результате сделки 200 млн руб. при рентабельности сделки для банка 20% годовых по сложной ставке.
Р = 200 (1 – 0,2)5 =65,536 млн руб.
8.4.2. СФЕРЫ ПРИМЕНЕНИЯ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ
Финансовые вычисления используются для решения широкого круга задач: от простейших расчетов по начислению простых и сложных процентов, определению эквивалентности процентных ставок и до количественного анализа потоков платежей, эквивалентного изменениям параметров финансовых сделок, ранжирования вариантов инвестиций, разработки планов погашения долгосрочных кредитов и займов, оценке финансовой эффективности различных кредитных и коммерческих операций.
8.4.2.1. Ежемесячное погашение кредита при использовании метода аннуитета
Смысл в том, что взята некая сумма на некоторый срок, которая погашается равными ежемесячными частями. При этом, ставка процента применяется только к основной сумме долга, которая в свою очередь постоянно уменьшается. Это принцип доливаемого стакана. В средневековой Европе был следующий метод застолья, при котором алкоголя организм получал мало, но общий объем выпитого был достаточно большой. За столом 10 человек (отец семейства, его 6 сыновей, 3 гостя) и 2-х литровый кувшин алкогольного напитка. Застолье продолжается полтора часа. За это время произносят 5 тостов. Каждый раз мужчины пьют из полного стакана. 1-й тост – выпивается пол стакана. И после этого каждый разбавляет свой стакан водой. 2-й тост – аналогично.
Ежемесячный платеж по кредиту содержит плату за пользование кредитом и частичное погашение суммы основного долга.
Вот и получается, что заёмщик в первый месяц платит самые большие проценты – на основную сумму долга, а уже во 2-й месяц процентов будет меньше.
Базовая формула:
P ��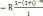 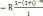
Текущая стоимость аннуитета.
P = R *[{1 – (1+i)-n}/i]
P = R *[{1 – (1+i)^-n}/i]
при однократном начислении процентов в год, тогда при многократном начислении процентов в год нужна формула:
P = R *[{1 – (1+i/m)^-n*m}/(i/m)],
где P – текущая (первоначальная) сумма долга. То есть просто размер кредита.
i – годовая ставка процента в долях.
i = I% /100%,
где I – годовая ставка процента в математических процентах.
n – количество периодов начислений, в годах.
m – количество начислений в год.
R – размер единичного платежа/взноса в счет погашения долга и выплаты процентов.
R = S / n при однократном начислении процентов в год и R = S / (n * m).
где S – будущая стоимость долга.
То есть сколько всего предстоит вернуть с учетом процентов. S = R * n при однократном начислении процентов в год и S = R * n * m.
а) Определение текущей и будущей стоимости ренты
Рента – это серия периодически осуществляемых платежей. Примером потоков с платежами произвольной величины могут служить выплаты дивидендов по обыкновенным акциям, капиталовложения в долгосрочные активы и т.д. Расчет характеристик таких потоков представляет собой определенные вычислительные трудности. В финансовых расчетах обычно возникает вопрос определения обобщающих характеристик – наращенной суммы ренты и современной величины ренты. Наращенная сумма ренты представляет сумму всех периодических платежей с начисленными на них процентами к концу ее срока. Современная величина ренты – это сумма всех периодических платежей, дисконтированных на начало срока ренты.
Если рента состоит из платежей одинакового размера и они осуществляются через одинаковые промежутки времени, то количество денег, которое может быть инвестировано в ренту, определяется по формуле текущей стоимости ренты (постнумерандо):
PV = Rс+Rс +…..+ Rс , (1)
(1+ i) (1+ i)2 .... (1+ i)n
или:
PV = ∑ Rс ,
(1+ i)n
или:
PV = Rс – 1• Rс , (1а)
i (1+ i)n i
где PV – текущая стоимость ренты;
Rс – ежегодные выплаты равными суммами; (член ренты)
i – процентная ставка (коэффициент окупаемости капиталовложений, предпочтительный для инвестора).
Пример. Компания сдает в аренду имущество сроком на 5 лет, арендная плата составляет 50 млн руб. в год, определен барьерный коэффициент рентабельности в 20%. Следовательно, общая сумма платежей за 5 лет составит 250 млн руб. Текущая стоимость арендной платы cоставит:
PV = 50 – 1 • 50 = 149,5 млн.руб.
0,2 (1+ 0,2)5 0,2
Для расчета будущей стоимости обыкновенной ренты (постнумерандо) применяется формула:
FV = R ∑ (1+ i)n, (2)
или
FV = R • (1+ i)n– 1 , или: FV = R • (1+ i)n– R , (2а)
iii
где FV – будущая стоимость аннуитета;
R – ежегодные вклады равными суммами; (член ренты)
i – процентная ставка (коэффициент наращивания капиталовложений, предпочтительный для инвестора).
Подобные расчеты в страховании называют актуарными. Они позволяют рассчитать объем потоков денежных средств, накопленную сумму страхового фонда и т.д.
Пример. Для погашения пакета облигаций, выпущенных на 5 лет, создается погасительный фонд при ежегодных платежах по 20 млн руб., на которые начисляются проценты по ставке 10%. Определим итоговую (наращенную) сумму при условии, что проценты начисляются один раз в год.
FV = 20 • (1 +0,l)5 – 20 =1,61051х200-200= 122,102 млн руб.
0.10.1
Таким образом, по истечении 5 лет предприятие накопит 122,1 млн руб. для погашения пакета выпущенных облигаций.
б) Расчет текущей стоимости и доходности ценных бумаг
Напомним, что стоимость ценной бумаги это абсолютная величина. Различают: номинальную и рыночную стоимость.
Доходность – это относительная величина: в общем виде это отношение дохода от данного финансового актива к объему инвестиций. Различают купонную и текущую доходность, доходность к сроку погашения.
Текущая рыночная стоимость любой ценной бумаги в общем виде может быть рассчитана по следующей формуле:
РV = ∑ CFп, (1)
(1+ r)n
где CFп – ожидаемый денежный поток в п -периоде;
r– приемлемая норма доходности.
Таким образом, подставляя в эту формулу предполагаемые поступления, норму дохода и период прогнозирования, можно рассчитать текущую стоимость любого финансового актива. Приемлемая норма доходности может устанавливаться инвестором следующими способами:
* в размере процентной ставки по банковским депозитам;
* исходя из процента, выплачиваемого банком вкладчику за хранение его средств, и надбавки за риск инвестирования в данный финансовый актив;
* исходя из процента, выплачиваемого по правительственным облигациям, и надбавки за риск.
8.4.2.2. Оценка облигаций Оценка облигаций с нулевым купоном
Это самый простой случай. Поскольку денежные поступления по годам, за исключением последнего, года равны нулю, формула имеет вид:
PV = CF ,
(1 + r ) n
где: PV – стоимость облигации с позиции инвестора;
CF – сумма, выплачиваемая при погашении облигации (CF = C• n + N);
n – число лет, по истечении которых произойдет погашение облигации
Оценка бессрочных облигаций
Бессрочная облигация предусматривает неопределенно долгую выплату дохода в установленном размере CF или по плавающей процентной ставке.
Поэтому:
PV = CF / r,
где r – приемлемая норма дохода.
Оценка срочных купонных облигаций
Расчет текущей стоимости облигаций при регулярных выплатах купонного дохода определяется по следующей формуле:
РVt = ∑ С +N, (2)
(1+ r) t (1+ r)n
где РVt – полная текущая стоимость облигации в периоде t;
С – размер ежегодного купонного дохода;
N – нарицательная стоимость облигации;
n – время, оставшееся до погашения облигации;
t – порядковый номер года с момента эмиссии;
r–требуемая норма доходности (доходность к сроку погашения).
C = N ·ik,где: ik – ставка купонного дохода (купонная доходность);
Текущая доходность облигации: ip = ΣC,
Pm
где Pm – цена приобретения облигации (рыночная).
Текущую доходность облигации можно определить за любой период владения облигацией. Для этого мы суммируем то количество купонных доходов, которые успеем получить.
Доходность к сроку погашения (YTM) – норма внутренней доходности по облигации, т.е. дисконтный множитель, устанавливающий равенство между текущей стоимостью и нынешней рыночной ценой (т.е. если Pm = PV, тоr = YTM).
Оценка акций
По привилегированным акциям предусматривается неопределенная по сроку долговая выплата дохода в установленном размере Dили по плавающей процентной ставке. При постоянных денежных потоках формула (1) трансформируется в формулу с бесконечным числом периодов:
Р V = D /i при n-. ∞ (3) V = D /i при n-. ∞ (3)
В отношении обыкновенных акций имеются различные методы оценки. Наиболее распространенным является метод, основанный на оценке будущих поступлений. В зависимости от предполагаемой динамики дивидендов конкретное представление формулы (1) меняется.
Базовыми могут быть три варианта динамики прогнозных значений дивидендов:
* дивиденды не меняются (ситуация аналогична ситуации с привилегированными акциями, т.е. применяется формула (3);
* дивиденды возрастают с постоянным темпом прироста;
* дивиденды возрастают с изменяющимся темпом прироста.
Допустим, базовая величина дивиденда равна D и ежегодно она увеличивается с темпом прироста g. Тогда формула (1) принимает вид:
PV = D (1 + g ) , (4 )
i–g
Из формулы (4) видно, что текущая цена обыкновенной акции очень чувствительна к параметру g, т.е. даже незначительное его изменение может существенно повлиять на цену. Эта формула применяется:
когда вы собираетесь хранить акции достаточно долго и делает акцент на получение дохода в виде дивиденда;
для оценки экстремальных значений, при которых еще выгодно или уже не выгодно приобретать акции.
ip = ΣD,
Pm
Где: D – ожидаемый дивиденд;
Pm – текущая рыночная цена акции.
Денежный оборот
Если построить модель системной динамики совокупной стоимостной оценки средств, участвующих в воспроизводственном процессе (А), и денежного капитала предприятия (Р). Модель будет состоять из уровней, потоков средств, участвующих в воспроизводственных процессах, и потоков капитала. Уровни определяют статическое состояние системы. Состояния уровней и потоки капитала определяют решения, которые управляют потоками средств, участвующих в воспроизводстве.
Если уровни характеризуют статическое состояние системы и описываются простыми уравнениями денежного оборота предприятия, то потоки перемещают содержание уровней и являются причиной изменения состояний. Уравнения потоков – следствие того, как понимают и оценивают менеджеры различные факторы и каким образом информация об уровнях приводит к выбору решений.
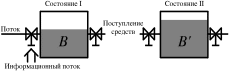
Введем понятие условного потока. Он, как и простой поток, меняет содержание уровней, но фактического перемещения средств не вызывает. Его понятие необходимодля сбалансированности между совокупной оценкой средств (А) и совокупным денежным капиталом (Р). В нижеприведенной модели будут прослеживаются и условные потоки:
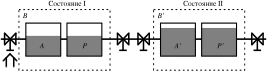
Нормальное состояние данной системы – равновесие – когда Р=А. Рассмотрим пример условного потока данной модели (модель 1-го порядка).
Модель B находится в состоянии I. Допустим, предприятие получает от поставщиков товары, не оплатив их. Возникает кредиторская задолженность. Объект моделиА переходит в А'. Однако тут же возникает условный поток от А' к Р. В свою очередь Рпереходит в состояние P'. Уравнение нормального состояния восстановлено: Р'=A' и система переходит в состояние равновесия B'.
Детализировав вышеприведенную модель и разбив А и Р на элементы, получим
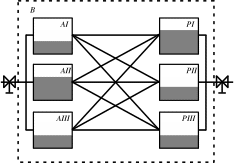
На основе потока информации финансовый менеджер может прогнозировать падение спроса, объемов реализации и товарных запасов. Допустим, мы прогнозируем снижение спроса на свою продукцию. Тогда мы должны, например, изменить ассортимент, диверсифицировать вложения, найти себе новых поставщиков или рынки сбыта. Однако, собственных средств для этих мероприятий нам будет мало и мы привлечем заемный капитал. Из-за этого появится еще один мощный входящий поток (обозначим его IвхR), вызывающий увеличение оборотных средств и, как следствие, условный поток для соблюдения балансового равновесия и нормального финансового состояния.
Если рост собственного оборотного капитала менее или равен росту всего денежного капитала предприятия при росте реализации, увеличивается разрыв между фактическим наличием собственного оборотного капитала и реальной в нем потребностью. Поэтому инфляционное воздействие на объем реализации "обесценивает" собственный капитал. Так как собственный оборотный капитал – главный источник накоплений предприятий, то его обесценение приводит к снижению товарных запасов, ухудшает инвестиционную активность и положение предприятий. Снижение темпов роста собственного оборотного капитала связано с опережающим ростом затрат над прибылью, что мешает осуществлению принципа самофинансирования. Эта проблема решается созданием условий для роста прибыли: снижением темпов инфляции, затрат, привлечения реальных денег от инвесторов и осуществления целенаправленной эмиссионной деятельности.
Анализ вышеизложенной модели позволяет прогнозировать изменения состояния источников финансирования а также выбрать оптимальную модель структуры денежного капитала.
|
 Скачать 1.35 Mb.
Скачать 1.35 Mb.
 еравномерные доходы и расходы (долгосрочные инвестиции)
еравномерные доходы и расходы (долгосрочные инвестиции)
 V = D /i при n-. ∞ (3)
V = D /i при n-. ∞ (3)

