Курсовая 1 Марковские процессы с дисретным временем. иркутский государственный университет
 Скачать 174.35 Kb. Скачать 174.35 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» (ФГБОУ ВПО «ИГУ») Институт математики, Кафедра «Теории вероятностей и экономики и информатики и дискретной математики» Марковские цепи с конечным числом состояний и дискретным временем курсовая работа студента 5 курса группы 2521-ЗБ специальности «Прикладная математика и информатика» Синицына Романа Михайловича Научный руководитель: к.ф.м.н. доцент кафедры Теории вероятностей и дискретной математики Колокольникова Наталья Арсеньева _____________________ подпись Содержание Введение…………………………………………………………. 3 Глава 1. Базовые определения…………………………………..4 Марковский процесс……………………………………………..4 Графы состояний переходов. Однородная цепь Маркова….….5 Глава 2. Матричное представление марковских цепей………..7 Матрица состояний переходов………………………………….7 Равенство Маркова………………………………………………9 Глава 3. Поглощающие процессы………………………………12 Цепи с поглощающими экранами………………………………12 Случайные блуждания…………………………………………..13 Задача о разорении игрока………………………………………15 Список литературы………………………………………………17 Введение Андрей Андреевич Марков является первооткрывателем обширного класса стохастических процессов с дискретной и непрерывной временной компонентой, названных Марковские процессы. На тот момент, во время ее построения, теория марковских процессов считалась абстрактной, но в настоящее время практические применения данной теории чрезвычайно многочисленны. Теория цепей Маркова выросла в огромную и весьма важную область научных исследований – теорию марковских случайных процессов, которая, в свою очередь, представляет основу общей теории стохастических процессов Марков А.А. сделал крупнейший вклад в теорию случайных процессов и теорию вероятностей в целом. В данной работе мы рассмотрим дискретные марковские процессы, определения и примеры. Марковская цепь Пусть имеется некоторая система S, состояние которой меняется с течением времени. Если состояние системы S меняется во времени случайным, заранее непредсказуемым образом, говорят, что в системе протекает случайный процесс. Случайный процесс называется марковским, если вероятность перехода системы в новое состояние зависит только от состояния системы в настоящий момент и не зависит от того, когда и каким образом система перешла в это состояние. Марковские случайные процессы делятся на классы. Основными классифицирующими признаками являются: множество состояний, в которых может находиться система моменты времени, в которых происходит изменение состояния системы. Случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы S1, S2, S3, ... являются конечным, счетным числом. Сам же процесс состоит в том, что система мгновенно переходит из одного состояния в другое в определенные моменты времени 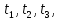 …. ….Кроме процессов с дискретными состояниями существуют случайные процессы с непрерывными состояниями: для таких процессов характерен постепенный, плавный переход из состояния в состояние. Например, процесс изменения напряжения в осветительной сети представляет собой случайный процесс с непрерывными состояниями. Если переходы системы из состояния в состояние возможны только в определенные моменты времени t1, t2, t3,…, то марковский процесс относится к процессам с дискретным временем. В противном случае имеет место процесс с непрерывным временем. Марковский процесс с дискретным состоянием и дискретным временем называют цепью Маркова. Графы состояний переходов Анализ случайных процессов с дискретными состояниями обычно проводится с помощью графа состояний и переходов.   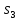 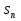 …... Рисунок 1. Пример графа системы S с n дискретными состояниями для блуждающей точки ( 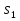 , , 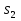 , ,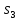 ,… ,…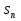 ) )Обозначим каждое состояние кругом, а возможные переходы из состояния в состояние — стрелками, соединяющими эти круги. Удобно также пользоваться размеченным графом, который графически изображает не только возможные состояния системы и возможные переходы из состояния в состояние, но также и значения вероятностей перехода.  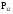 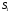 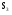 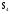 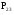 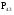 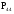 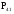 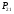 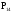 Рисунок 2. Примеры графа состояний и переходов В данном примере (рис. 2) рассматривается цепь Маркова, включающая четыре состояния. С помощью данного графа можно увидеть полную картину вероятностей перехода. К примеру, вероятность перехода из состояния 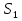 в состояние в состояние 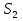 равна равна 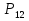 , а вероятность состояния , а вероятность состояния 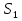 остаться в том же состоянии за 1 переход равна нулю. остаться в том же состоянии за 1 переход равна нулю.Отдельно можно рассмотреть состояние 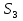 , попав в которое, система больше не может попасть в любое другое состояние. Такое состояние называется поглощающим. , попав в которое, система больше не может попасть в любое другое состояние. Такое состояние называется поглощающим.Для любой цепи Маркова по ее переходной матрице можно построить ее полный граф. Справедливо и обратное, если дан граф цепи Маркова, то по нему можно построить и переходную матрицу цепи Маркова. Возвращаясь к рисунку 2, матрица переходов для данного графа будет иметь вид 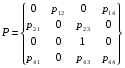 Вероятности 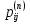 называются вероятностями перехода из i в j на n-ом шаге. называются вероятностями перехода из i в j на n-ом шаге.Если вероятность перехода не зависит от n, то есть в каждый момент n остается одинаковой, такой что 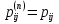 , то цепь Маркова называется однородной , то цепь Маркова называется однороднойИными словами однородной цепью Маркова является такая цепь, для которых условная вероятность 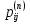 перехода из состояния i в состояние jне зависит от номера испытания. перехода из состояния i в состояние jне зависит от номера испытания.Матрица состояний переходов Графу системы, содержащему n вершин, можно поставить в соответствие матрицу n×n, элементами которой являются вероятности переходов pij между вершинами графа, называемую матрицей вероятностей переходов. Определение. Матрица, составленная из элементов pij (вероятностей переходов) называется матрицей переходов однородной цепи Маркова. 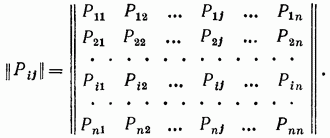 Где индекс i - откуда переход; индекс j- куда переход. Элементы 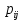 матрицы матрицы 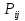 удовлетворяют условиям: удовлетворяют условиям:1) 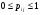 , , 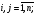 2) 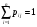 , , 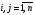 Условие 2 означает, что переходы из состояний i во все другие и в само себя составляют полную группу событий. Построчные суммы всех вероятностей равны 1, так как в любой момент времени система обязательно с вероятностью 1 перейдет из состояния 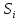 в какое-либо другое состояние или в само себя ( в какое-либо другое состояние или в само себя (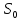 , ,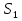 ,…, ,…,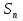 ) )Матрица, обладающая этими свойствами называется стохастической, или вероятностной. Т.к. элементами стохастической матрицы P являются вероятности перехода 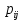 , то эту матрицу называют матрицей вероятностей перехода. , то эту матрицу называют матрицей вероятностей перехода.Рассмотрим несколько простых примеров марковских цепей. В данном случае рассмотрим случайные блуждания, связанные с неограниченными испытаниями Бернулли. Представим объект, который движется по прямой линии единичными шагами. Каждый шаг вправо происходит с вероятностью p, а шаг влево с вероятностью q. Объект движется до тех пор, пока не достигнет одной из двух крайних точек, которые называются граничными точками. Возможные поведения в этих точках приводят к различным цепям Маркова. Рассмотрим случай пяти состояний когда состояния 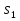 и и 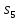 будут граничными, а состояния будут граничными, а состояния 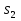 , , 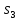 , , 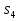 – внутренними. – внутренними.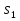 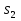 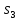 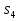 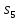 Пример 1. Допустим, что процесс, достигнув состояний 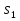 или или 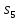 , остаются там навсегда. В этом случае матрица перехода имеет вид , остаются там навсегда. В этом случае матрица перехода имеет вид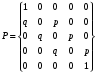 Можно наглядно увидеть, что состояния 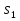 и и 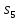 являются поглощающими состояниями, так как из этих состояний нельзя попасть в любые другие состояния. являются поглощающими состояниями, так как из этих состояний нельзя попасть в любые другие состояния.Пример 2. Предположим теперь, что, достигнув одного из граничных состояний, частица с вероятностью 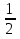 в нем остается и с вероятностью в нем остается и с вероятностью 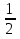 переходит в другое граничное состояние. В этом случае матрица имеет вид переходит в другое граничное состояние. В этом случае матрица имеет вид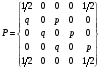 Равенство Маркова Обозначим через 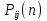 вероятность того, что в результате n шагов (испытаний) система перейдет из состояния iв состояние j. вероятность того, что в результате n шагов (испытаний) система перейдет из состояния iв состояние j. Возникает вопрос, как, зная переходные вероятности 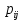 , найти вероятности перехода состояния iв состояние j за n шагов. С этой целью вводится в рассмотрение промежуточное (между iи j) состояние r. Другими словами, полагают, что из первоначального состояния iза m шагов система перейдет в промежуточное состояние r с вероятностью , найти вероятности перехода состояния iв состояние j за n шагов. С этой целью вводится в рассмотрение промежуточное (между iи j) состояние r. Другими словами, полагают, что из первоначального состояния iза m шагов система перейдет в промежуточное состояние r с вероятностью 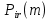 , после чего за оставшиеся (n–m) шагов из промежуточного состояния r она перейдет в конечное состояние jс вероятностью , после чего за оставшиеся (n–m) шагов из промежуточного состояния r она перейдет в конечное состояние jс вероятностью 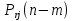 . . Используя формулу полной вероятности, можно показать, что справедлива формула 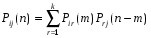 Эту формулу называют равенством Маркова. Зная все переходные вероятности 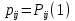 , т.е. зная матрицу перехода , т.е. зная матрицу перехода 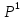 из состояния в состояние за один шаг, можно найти вероятности из состояния в состояние за один шаг, можно найти вероятности 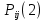 перехода из состояние в состояние за два шага, а значит, и саму матрицу перехода перехода из состояние в состояние за два шага, а значит, и саму матрицу перехода 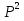 , далее – по известной матрице , далее – по известной матрице 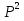 - найти - найти 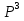 и т.д. и т.д.Действительно, полагая в равенстве Маркова n=2, m=1 получим 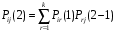 или 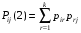 . .В матричном виде это можно записать как 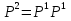 . .Полагая n=3, m=2, получим 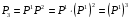 В общем случае справедливо соотношение 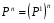 Так же стоит сказать и о векторе начального состояния 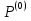 , который показывает начальное распределение системы в момент времени , который показывает начальное распределение системы в момент времени 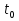 . .Компоненты данного вектора – это вероятности 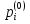 , которые показывают, в каких состояниях находится система в начальный момент времени , которые показывают, в каких состояниях находится система в начальный момент времени 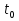 . . То есть вектор начального перехода записывается таким образом: P(0) = (p(0)(1),…, p(0)(k)) где 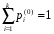 Аналогичным образом определяются векторы P(n) = (p(n)(1),…, p(n)(k)) где 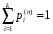 , , 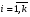 , k –число состояний системы , k –число состояний системыТаким образом видно, что P1 = P(0) 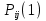 , а значит , а значит Pn = P(n-1) 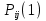 = P(0) = P(0) 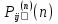 Для иллюстрации приведем простой пример. Рассмотрим процесс функционирования некоторой системы (например, прибора). Пусть прибор в течение одних суток может находиться в одном из двух состояний – исправном ( 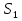 ) и неисправном ( ) и неисправном (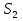 ). В результате массовых наблюдений за работой прибора составлена следующая матрица перехода ). В результате массовых наблюдений за работой прибора составлена следующая матрица перехода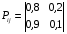 Пусть вектор начальных вероятностей состояний прибора задан соотношением 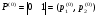 , ,где 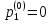 , , 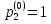 (в начальный момент прибор был неисправен). Требуется определить вероятности состояния прибора через трое суток. (в начальный момент прибор был неисправен). Требуется определить вероятности состояния прибора через трое суток.Решение: Используя матрицу перехода, определим вероятности состояний после первого шага (после первых суток): Вероятности состояний после второго шага (вторых суток) равны Наконец, вероятности состояний после третьего шага (третьих суток) равны Таким образом, вероятность того, что прибор будет находиться в исправном состоянии равна 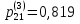 , и того, что в неисправном – соответственно , и того, что в неисправном – соответственно 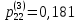 В матричной форме это будет выглядеть так: P3 = P(0) 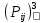 или 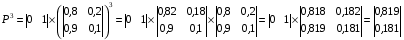 Цепи с поглощающими экранами При классификации состояний классы эквивалентности делятся на невозвратные и эргодические множества. Минимальные элементы частичного упорядочения классов эквивалентности называются эргодическими множествами. Состояния эргодического множества называются эргодическими (или возвратными) состояниями. В случае эргодического множества возможны любые переходы внутри множества, но исключены переходы из множества и в него. Состояния, входящие в невозвратное множество называют невозвратными состояниями. Иными словами можно сказать, что если процесс выходит из невозвратного множества, он уже не может вернуться обратно в это множество. В частности, если эргодическое множество состоит лишь из одного состояния, то это состояние такое, что, попав в него, уже нельзя из него выйти. Такое состояние называется поглощающим. Определение. Состояние 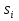 – поглощающее тогда и только тогда,когда – поглощающее тогда и только тогда,когда 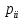 = 1 = 1
 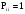 Рисунок 1 При попадании в поглощающее состояние процесс заканчивается. В любой конечной цепи Маркова, независимо от того, где начался процесс, вероятность после n шагов оказаться в эргодическом состоянии стремится к 1 при 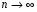 Действительно, если в какой-то момент времени система достигла эргодического состояния, то она навсегда останется в этом состоянии. При увеличении числа шагов вероятность увеличивается. Рассмотрим пример случайного блуждания с одним поглощающим экраном Частица находится в состоянии 1 в начальный момент времени на оси. Вероятность частицы переместиться вправо равна p, соответственно, вероятность переместиться влево равна q=1-p. Состояние, соответствующее координате 0 на оси ( 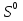 ) является поглощающим, и точка, попав в него, больше не сможет выйти. ) является поглощающим, и точка, попав в него, больше не сможет выйти.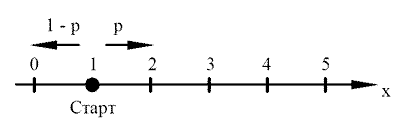 Рассмотрим ситуацию после первого шага: либо частица сдвинулась налево, попала в точку x = 0 и поглотилась с вероятностью q, либо сдвинулась направо в точку x = 2 с вероятностью p. Пусть P2 обозначает вероятность того, что частица поглощается в начале координат x = 0, если она выходит из точки x = 2. Формула полной для P1 вероятности будет 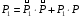 Здесь 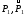 - вероятности, при условии, что сделан шаг вправо или влево - вероятности, при условии, что сделан шаг вправо или влевоТогда P1 = 1×q + P2 × р = q + P2 × р Теперь рассмотрим путь из х=2. Путь, ведущий к поглощению из x = 2 можно рассмотреть как движение к точке х=1, независимо от количества шагов, а затем из точки х=1 в точку х=0. Так как рассматривается марковский процесс, то вероятность, что когда-нибудь точка перейдет из состояния 2 в 1 такая же, как и вероятность перехода из состояния 1 в состояние 0. Следовательно, можно записать виде 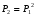 Подставив 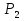 получим квадратное уравнение получим квадратное уравнение P1 = q + 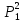 × р × ркорни которого: 1. 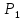 = 1 , = 1 , 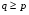 2. 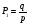 , q < p , q < pСразу можно сказать чему равняется вероятность попадания в поглощающее состояние из точки x=m 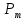 = = 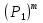 = = 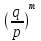 , q < p , q < pЗадача о разорении игрока Игрок M имеет m денежных единиц, игрок N - n единиц. После каждой игры один игрок выигрывает, другой проигрывает единицу. В каждой партии вероятность выигрыша игрока M равна p, а выигрыша N равна q = 1 - p. Игра продолжается до разорения одного из игроков. Игрок начинает с положения x = m. Когда x = 0, он разорен, при x = m + n банкротом является игрок N.
Мы уже знаем, что если игрок M играет против банка с неограниченными ресурсами, то становится банкротом с вероятностью (q/p)m. По пути к банкротству он либо получает сумму m + n (n теперь конечно) либо никогда не будет иметь ее на руках. Пусть вероятность того, что он проиграет игроку N, равна Q (это событие равносильно выигрышу N у банка с неограниченным капиталом без достижения игроком M суммы m + n). Тогда (p/q)m = Q + (1 - Q)·(q/p)m+n, (1) поскольку Q есть доля последовательностей, для которых поглощение произойдет до достижения точки m + n, а 1 - Q - доля тех последовательностей, которые достигают положения m + n; (q/p)m+n есть доля последовательностей, поглощаемых в нуле, если игра продолжается неограниченно долго. Тогда P = 1 - Q есть вероятность того, что игрок M выиграет. Из (1) находим P = [1 - (q/p)m] / [1 - (q/p)m+n]. (2) В нашем случае p = 2/3, q = 1/3, m = 1, n = 2 и P = 4/7, и, значит, лучше быть вдвое более искусным в игре, чем вдвое более богатым. Если q = p = 1/2, то P в уравнении (2) принимает неопределенную форму 0/0. Применение правила Лопиталя дает P = m / (m + n). (3) Таким образом, если игроки равноискусны, то шансы на выигрыш игрока M равны 1/3, а его средний выигрыш равен 1/3•2 + 2/3•(-1) = 0. Игра в этом случае безобидна, т. е. математическое ожидание выигрыша равно нулю для каждого игрока. Список литературы Вентцель Е.С. Теория вероятностей: Учеб. для вузов. — 6-е изд. стер. — М.: Высш. шк., 1999.— 576 c. Дж. Кемени, Дж. Снелл Конечные цепи Маркова: М.: Наука, 1970. — 272 стр. Колокольникова Н.А. Гильманшин Р.Р Случайные процессы: Учебное пособие. — Изд. ИГУ, 2012. — 101 стр. http://e-biblio.ru/book/bib/06_management/teor_mass_obslug/158.9.13.html http://stu.sernam.ru/book_rop.php?id=41 https://studfiles.net/preview/845446/page:22/ http://termist.com/bibliot/stud/50_prob/36_1.htm Иркутск 2017 |