Главная страница
Навигация по странице:

  • 6 ОЦЕНКА ВЛИЯНИЯ ВНУТРЕННЕЙ ОС ПО ЭДС

  • 7 РАСЧЕТ И ПОСТРОЕНИЕ СКОРОСТНЫХ ХАРАКТЕРИСТИК

  • 8 РАСЧЕТ ДИНАМИЧЕСКОГО ПАДЕНИЯ И ОСЦИЛЛОГРАММЫ СКОРОСТИ

    		•

    Курсовой по Соколову. Исследование динамических процессов работы привода


    Скачать 1.1 Mb.
    НазваниеИсследование динамических процессов работы привода
    Дата10.03.2021
    Размер1.1 Mb.
    Формат файлаdoc
    Имя файлаКурсовой по Соколову.doc
    ТипИсследование
    #183426
    страница3 из 4
    1   2   3   4

    5.2 Оптимизация контура скорости и расчет решающих цепей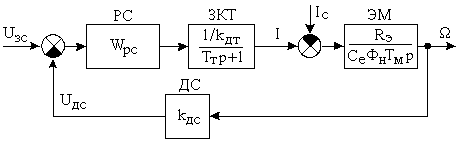

    Рисунок 9 - Структурная схема контура скорости
    На рисунке 9 представлена схема контура скорости. Её составляющие:

    - РС - регулятор скорости;

    - ЗКТ - замкнутый контур тока;

    - ЭМ - электромеханическая часть;

    - ДС - датчик скорости.

    По заданию контур скорости должен быть с П-регулятором, то есть двукратно интегрирующий. Следовательно, настройку необходимо делать на модульный оптимум (МО). Передаточная функция разомкнутого контура скорости при настройке на МО: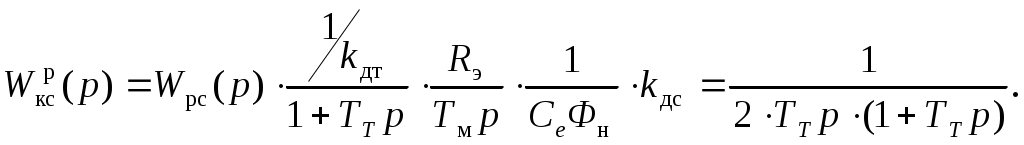

    (5.16)
    Передаточная функция регулятора скорости:

    (5.17)

    где - коэффициент регулятора скорости. (5.18)

    Передаточная функция замкнутого контура скорости: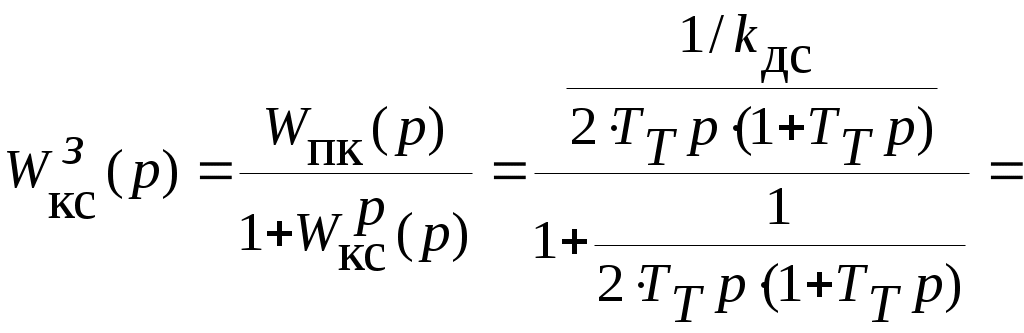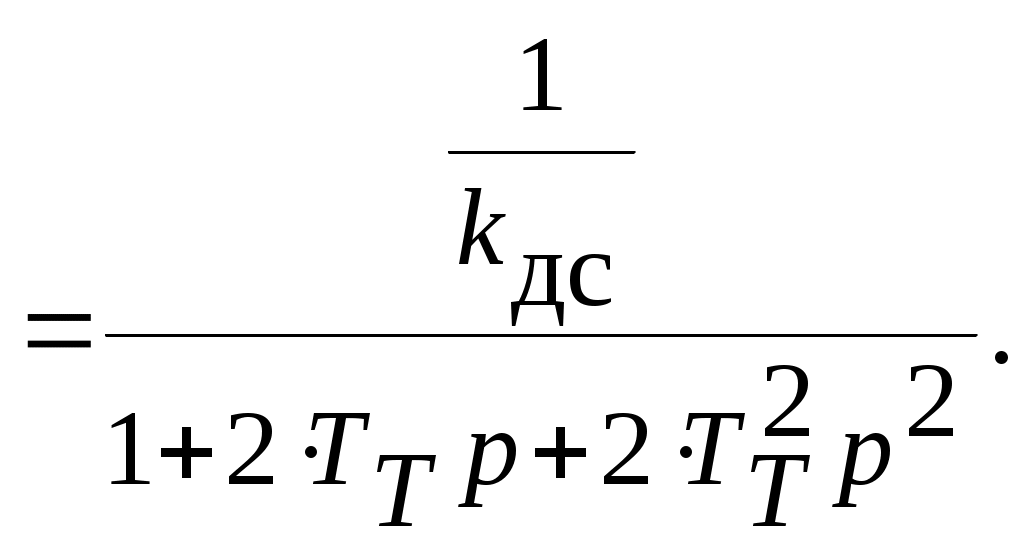



    (5.19)




    Передаточная функция оптимизированного на МО замкнутого контура скорости с фильтром на входе:

    (5.21)

    где (с) - эквивалентная постоянная времени контура скорости, настроенного на МО.

    Произведем расчет решающих цепей контура скорости. Схема контура скорости представлена на рисунке 10.

    Скорость холостого хода двигателя:

    (рад/с). (5.22)

    Коэффициент передачи датчика скорости:

    (В·с/рад). (5.23)

    Коэффициент усиления регулятора скорости найдем по формуле (5.18):



    Примем резистор в цепи обратной связи регулятора скорости

    (кОм).

    Сопротивление в цепи датчика скорости:

    (кОм). (5.25)

    Условие установившегося режима:

    , (5.26)

    где - максимальное напряжение задания на скорость;

    - максимальное выходное напряжение датчика скорости.

    Принимая (В), получаем:

    (кОм). (5.27)

    Коэффициент делителя:

    . (5.29)

    Величину сопротивления R4принимаем:

    R4 = 1(кОм).

    Тогда величину сопротивления R3 находим как:

    (кОм) (5.30)

    Напряжение стабилизации стабилитронов:

    (В), (5.31)

    где (В) - максимальное напряжение на выходе регулятора скорости;

    (В) - падение напряжения на стабилитроне.

    Согласно пункту 1.9 данной курсовой работы суммарное сопротивление задатчика скорости 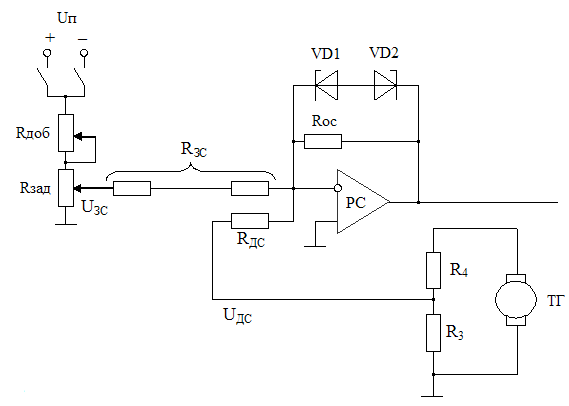(кОм). Так как (В), а напряжение питания (В), то необходимо добавить подстроечный резистор (Ом) на котором будет падение напряжения в 5 В.


    Рисунок 10 - Схема контура скорости.
    6 ОЦЕНКА ВЛИЯНИЯ ВНУТРЕННЕЙ ОС ПО ЭДС
    Структурная схема контура тока с учетом влияния внутренней обратной связи по ЭДС представлена на рисунке 14.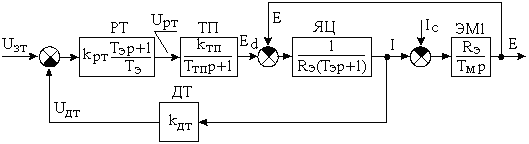


    Рисунок 14 - Структурная схема контура тока с учетом влияния внутренней обратной связи по ЭДС.
    Рассмотрим влияние внутренней обратной связи по ЭДС при отсутствии нагрузки на валу.Передаточная функция звена якорной цепи с учетом влияния внутренней обратной связи по ЭДС: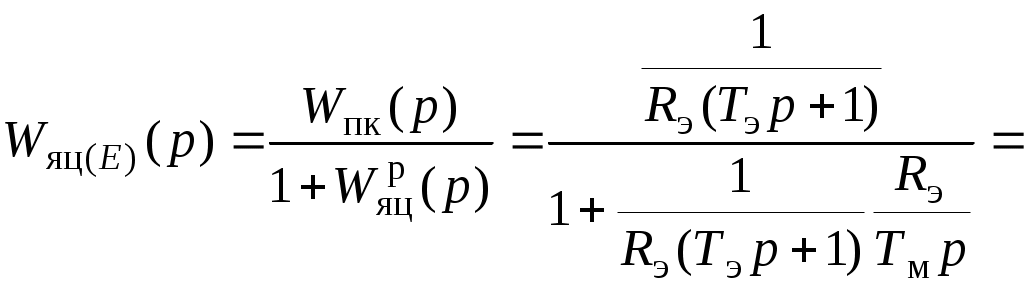



    . (6.1)

    Передаточная функция якорной цепи обладает дифференцирующими свойствами, благодаря чему компенсируются интегральные свойства регулятора.

    Передаточная функция разомкнутого контура тока с учетом действия внутренней обратной связи по ЭДС:



    . (6.2)

    Определим передаточную функцию замкнутого контура тока с учетом действия внутренней обратной связи по ЭДС: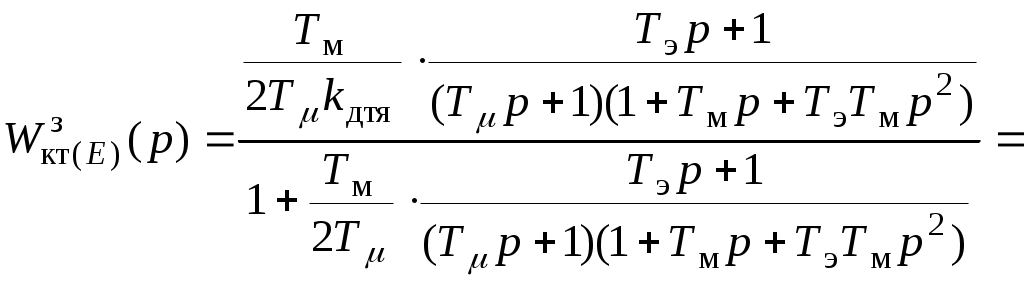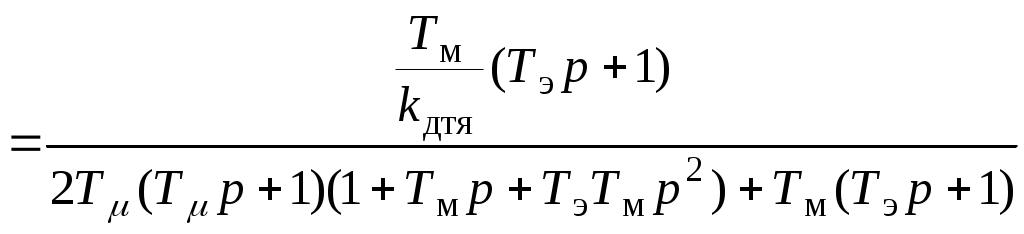



    . (6.3)

    Напряжение задания на номинальный ток:

    (В). (6.4)

    Для поиска установившегося значения тока применим теорему об установившемся значении оригинала: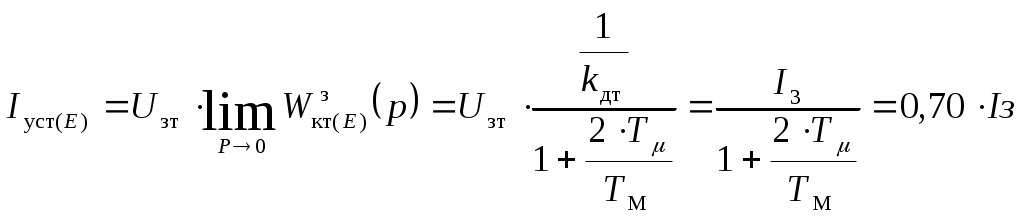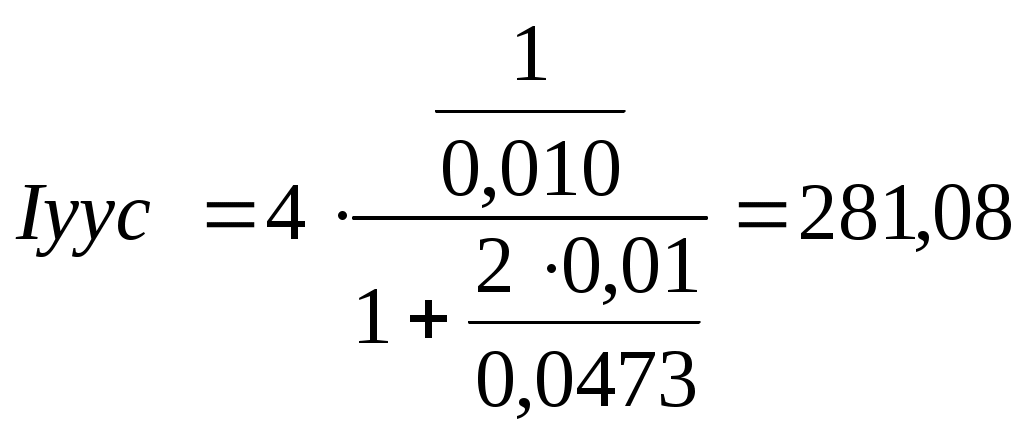


    (А). (6.5)

    Проведем моделирование переходных процессов в ПО SamSim. Схема контура тока с учетом влияния внутренней обратной связи по ЭДС представлена на рисунке 16.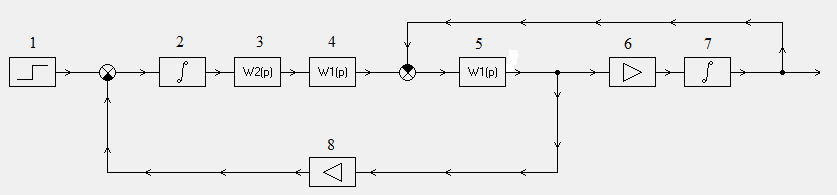



    Рисунок 15 - Схема контура тока с учетом действия внутренней ОС по ЭДС
    Состав схемы:

    - 1 - источник ступенчатого сигнала;

    - 2,3 - регулятор тока;

    - 4 - тиристорный преобразователь тока якоря;

    - 5 - якорная цепь электродвигателя;

    - 6,7 - электромеханическая часть;

    - 8 - датчик тока якоря(на базе шунта).

    Параметры звеньев:

    1) Источник ступенчатого сигнала. Высота ступеньки 5.

    2) Интегрирующие звено. Передаточная функция:

    . (6.10)

    3) Форсирующее звено первого порядка. Передаточная функция:

    . (6.11)

    4) Апериодическое звено первого порядка. Передаточная функция:

    . (6.12)

    5) Апериодическое звено первого порядка. Передаточная функция: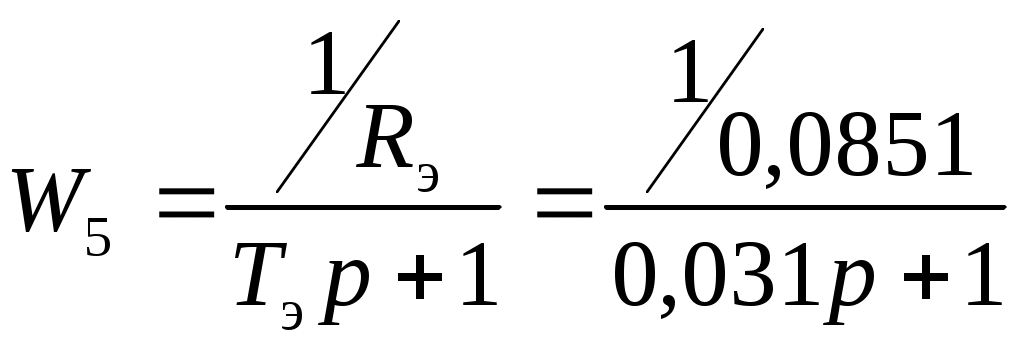

    . (6.13)

    6) Пропорциональное звено. Передаточная функция:

    . (6.14)

    7) Инегрирующие звено. Передаточная функция:

    . (6.15)

    8) Пропорциональное звено. Передаточная функция:

    . (6.16)
    Получившийся переходный процесс представлен на рисунке 17.
    Рисунок 17 - Осциллограмма тока при отработке сигнала задающего воздействия с учетом влияния внутренней ОС по ЭДС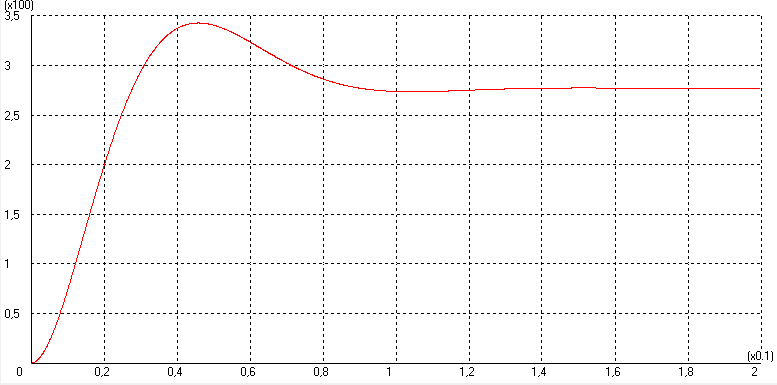


    Схема контура тока без учета влияния внутренней обратной связи по ЭДС представлена на рисунке 18.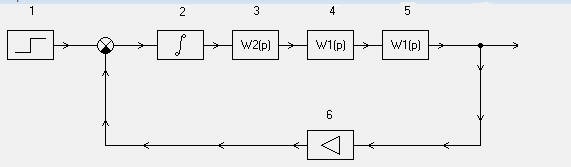



    Рисунок 18 - Схема контура тока при заторможенном двигателе
    Состав схемы:

    - 1 - источник ступенчатого сигнала;

    - 2,3 - регулятор тока;

    - 4 - тиристорный преобразователь тока якоря;

    - 5 - якорная цепь электродвигателя;

    - 6 - датчик тока якоря(на базе шунта).

    Параметры звеньев:

    1) Источник ступенчатого сигнала. Высота ступеньки 4.

    2) Интегрирующие звено. Передаточная функция:

    . (6.17)

    3) Форсирующее звено первого порядка. Передаточная функция:

    . (6.18)

    4) Апериодическое звено первого порядка. Передаточная функция:

    . (6.19)

    5) Апериодическое звено первого порядка. Передаточная функция: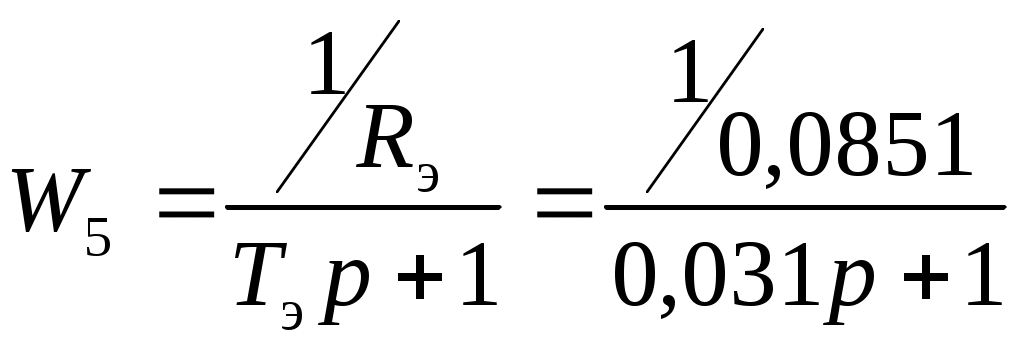

    . (6.20)

    6) Пропорциональное звено. Передаточная функция:

    . (6.21)

    Осциллограмма представлена на рисунке 19.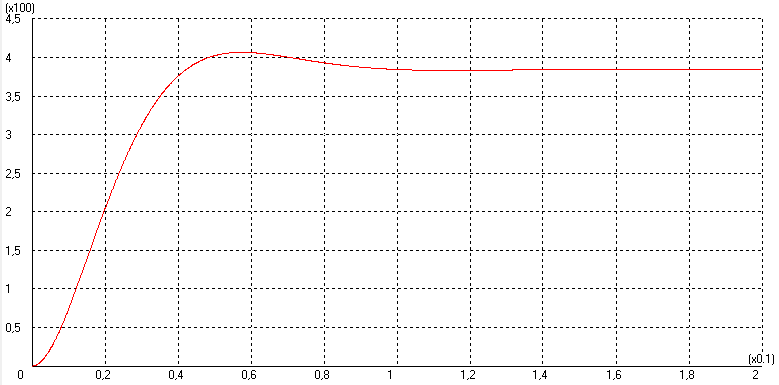



    Рисунок 19 - Осциллограмма тока при отработке сигнала задающего воздействия при заторможенном двигателе
    Результаты моделирования в ПО SamSim подтверждают результаты, полученные с помощью преобразования Лапласа.

    По результатам видно, что при одинаковом задающем сигнале, на выходе контура тока с учетом внутренней обратной связи по ЭДС появляется ошибка регулирования. То есть контур, который при расторможенном роторе был статичным, становится астатичным при заторможенном роторе.

    7 РАСЧЕТ И ПОСТРОЕНИЕ СКОРОСТНЫХ ХАРАКТЕРИСТИК
    Скоростные характеристики однозонного тиристорного электропривода с П-регулятором скорости при Uзс = 10В представляют собой прямые линии, выходящие из точки идеального холостого хода .

    Выражение для расчета характеристик имеет вид:

    , (7.1)

    где -посадка скорости.

    Скорость идеального холостого хода:

    (рад/с). (7.2)

    Падение скорости на естественной характеристике:

    . (7.3)

    Выражение для естественной характеристики:

    . (7.4)

    Падение скорости на естественной характеристике при номинальной нагрузке:

    (рад/с). (7.5)

    Статизм естественной характеристики:

    . (7.6)

    Падение скорости в разомкнутой системе:

    . (7.7)

    Выражение для разомкнутой системы:

    . (7.8)

    Падение скорости в разомкнутой системе при номинальной нагрузке:

    (рад/с). (7.9)

    Статизм разомкнутой системы:

    . (7.10)

    Падение скорости в замкнутой системе:

    . (7.11)

    Выражение для замкнутой системы:

    . (7.12)

    Падение скорости в замкнутой при номинальной нагрузке:

    (рад/с). (7.13)

    Статизм замкнутой системы:

    . (7.14)

    Построение характеристик дляUзс = 4В ( ).

    Скорость холостого хода:

    (рад/с). (7.15)

    Выражение для разомкнутой системы:

    . (7.16)

    Статизм разомкнутой системы:

    . (7.17)

    Выражение для замкнутой системы:

    . (7.18)

    Статизм замкнутой системы:

    . (7.19)

    Полученные характеристики изображены на рисунке 20.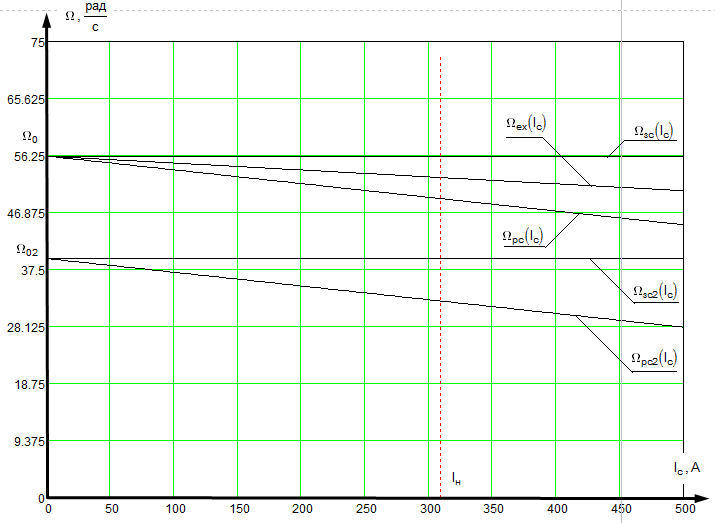



    Рисунок 20 - Скоростные характеристики электропривода

    По результатам можно отметить, что характеристика замкнутой системы абсолютно жёсткая и позволяет реализовать больший диапазон регулирования скорости.

    8 РАСЧЕТ ДИНАМИЧЕСКОГО ПАДЕНИЯ И ОСЦИЛЛОГРАММЫ СКОРОСТИ

    Для расчета динамического падения скорости используем аппарат передаточных функций. Передаточная функция скорости по возмущению (см. рисунок 9):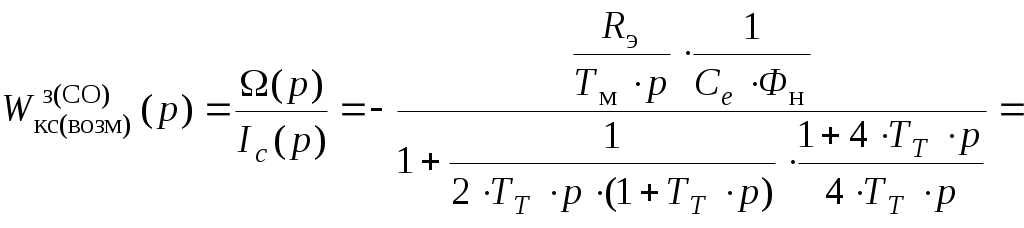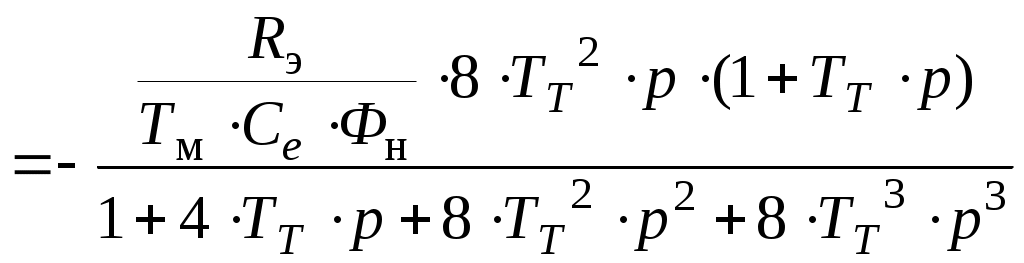



    . (8.1)

    Переходный процесс динамического падения скорости при набросе номинальной нагрузки Ic = Iн можно получить с помощью обратного преобразования Лапласа: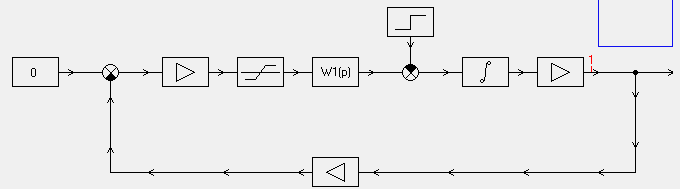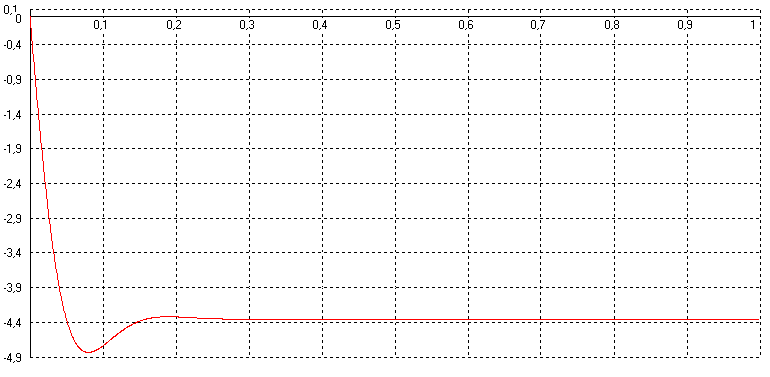




    Рисунок 21 - Осциллограмма скорости при набросе нагрузки
    График переходного процесса изображен на рисунке 21.

    Проведем моделирование наброса нагрузки в ПО SamSim. Схема представлена на рисунке 22.


    Рисунок 22 - Схема контура скорости в SamSim
    Состав схемы:

    - 1 - нулевой сигнал;

    - 2, 3 - регулятор скорости;

    - 4 - замкнутый контур тока;

    - 5 - сигнал нагрузки (Iс);

    - 6 - электромеханическая часть;

    - 7 - датчик скорости.
    Параметры звеньев:

    1) Нулевой сигнал.

    2) Инерционное звено. Передаточная функция:

    . (8.3)

    3) Форсирующее звено первого порядка. Передаточная функция:

    . (8.4)

    4) Апериодическое звено первого порядка. Передаточная функция: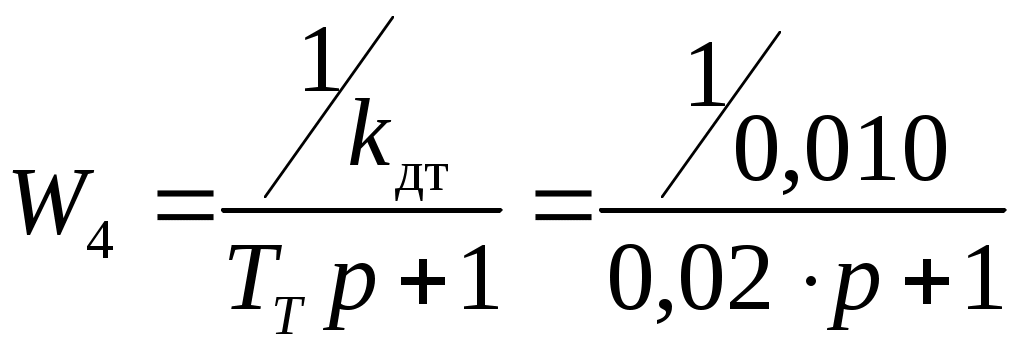

    . (8.5)

    5) Сигнал возмущения. Высота ступеньки 27,6

    6) Инерционное звено. Передаточная функция:

    . (8.6)

    7) Пропорциональное звено. Передаточная функция:

    . (8.7)

    На рисунке 23 представлена осциллограмма скорости при набросе нагрузки при нулевом задании.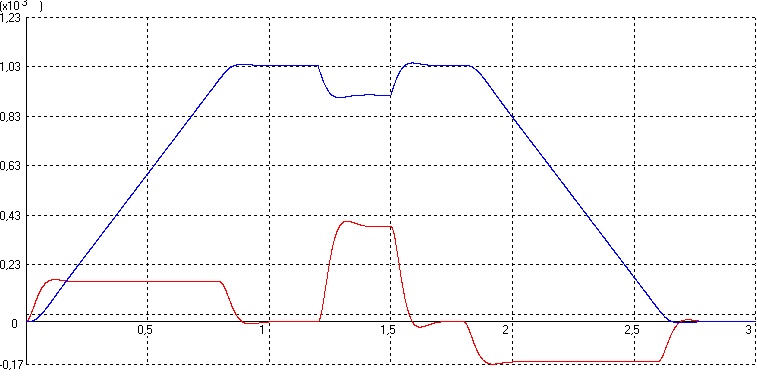



    Рисунок 23 - Осциллограмма скорости при набросе нагрузки в ПОSamSim
    По результатам видно, что посадка скорости в установившемся режиме в системе, оптимизированной на симметричный оптимум, равна нулю.
    1   2   3   4

    написать администратору сайта