реф. РЕФЕРАТ9. Исследование функций содержание основные теоремы дифференциального исчисления 1 Локальные экстремумы функции

• Название: Исследование функций содержание основные теоремы дифференциального исчисления 1 Локальные экстремумы функции
• Дата: 22.07.2022
• Размер: 0.94 Mb.
• Имя файла: РЕФЕРАТ9.rtf
• Тип: Исследование; #634677
• страница: 1 из 3

ВЫСШАЯ МАТЕМАТИКА
ИССЛЕДОВАНИЕ ФУНКЦИЙ

СОДЕРЖАНИЕ
1. Основные теоремы дифференциального исчисления

1.1 Локальные экстремумы функции

1.2 Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа

2. Исследование функций

2.1 Достаточные условия экстремума функции

2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба

2.3 Асимптоты графика функции

2.4 Общая схема построения графика функции

Литература

1. ОСНОВНЫЕ ТЕОРЕМЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
1.1 Локальные экстремумы функции
Пусть задана функция у = f (х) на множестве Х и х₀ – внутренняя точка множества Х.

Обозначим через U(х₀) окрестность точки х₀. В точке х₀ функция f (х) имеет локальный максимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х) £ f (х₀).

Аналогично: функция f (х) имеет в точке х₀ локальный минимум, если существует такая окрестность U(х₀) точки х₀, что для всех х из этой окрестности выполнено условие f (х) ³ f (х₀).

Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них – локальными экстремумами функции.

Пусть функция f (х) определена на отрезке [а, b] и имеет локальный экстремум на каком-то из концов этого отрезка. Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для «а» и левой для «b» полуокрестностью.

Проиллюстрируем данные выше определения: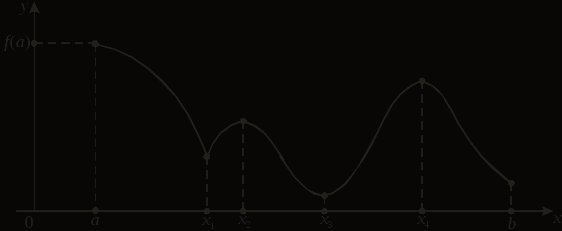

На рисунке точки х₁, х₃ – точки локального минимума, точки х₂, х₄ – точки локального максимума, х = а – краевого максимума, х = b – краевого минимума.

Заметим, что наряду с локальными минимумом и максимумом определяют так называемые глобальные минимумы и максимумы функции f(х) на отрезке [a, b]. На рисунке точка х = а – точка глобального максимума (в этой точке функция f(х) принимает наибольшее значение на отрезке [a, b]), точка х = х₃ – точка соответственно глобального минимума.
1.2 Основные теоремы дифференциального исчисления: Ферма, Ролля, Коши, Лагранжа
Рассмотрим некоторые теоремы, которые позволят в дальнейшем проводить исследование поведения функций. Они носят названия основных теорем математического анализа или основных теорем дифференциального исчисления, поскольку указывают на взаимосвязь производной функции в точке и ее поведения в этой точке. Рассмотрим теорему Ферма.

Пьер Ферма (1601–1665) – французский математик. По профессии – юрист. Математикой занимался в свободное время. Ферма – один из создателей теории чисел. С его именем связаны две теоремы: великая теорема Ферма (для любого натурального числа n > 2 уравнение хⁿ + yⁿ = zⁿ не имеет решений в целых положительных числах х, у, z) и малая теорема Ферма (если р – простое число и а – целое число, не делящееся на р, то а ^р-1 – 1 делится на р).

Теорема Ферма. Пусть функция f (х) определена на интервале (а, b) и в некоторой точке х₀ Î (а, b) имеет локальный экстремум. Тогда, если в точке х₀ существует конечная производная f '(x₀), то f '(x₀) = 0.

Доказательство.

Пусть, для определенности, в точке х₀ функция имеет локальный минимум, то есть f (х) ³ f (х₀), œх Î U(х₀). Тогда в силу дифференцируемости

f (х) в точке х₀ получим:

при х > х₀:

при х < х₀:

Следовательно, эти неравенства в силу дифференцируемости имеют место одновременно лишь когда



Теорема доказана.

Геометрический смысл теоремы Ферма: если х₀ Î (а, b) является точкой минимума или максимума функции f (х) и в этой точке существует производная функции, то касательная, проведенная к графику функции в точке (х₀, f (х₀)), параллельна оси Ох: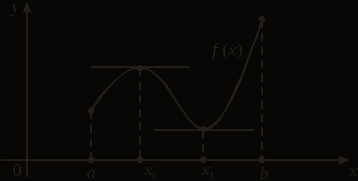


Заметим, что оба условия теоремы Ферма – интервал (а, b) и дифференцируемость функции в точке локального экстремума – обязательны.

Пример 1. у = çх÷, х Î (–1; 1).

В точке х₀ = 0 функция имеет минимум, но в этой точке производная не существует. Следовательно, теорема Ферма для данной функции неверна (не выполняется условие дифференцируемости функции в точке х₀).
Пример 2. у = х³, х Î [–1; 1].

В точке х₀ = 1 функция имеет краевой максимум. Теорема Ферма не выполняется, так как точка х₀ = 1 Ï (–1; 1).

Мишель Ролль (1652–1719) – французский математик, член Парижской академии наук. Разработал метод отделения действительных корней алгебраических уравнений.

Теорема Ролля. Пусть функция f (x) непрерывна на отрезке [а, b], дифференцируема на (а, b), f (а) = f(b). Тогда существует хотя бы одна точка x, а < x < b, такая, что f '(x) = 0.

Доказательство:

1) если f (x) = const на [a, b], то f '(х) = 0, œх Î (a, b);

2) если f (x) ¹ const на [a, b], то непрерывная на [a, b] функция достигает наибольшего и наименьшего значений в некоторых точках отрезка

[a, b]. Следовательно, max f (x) или min f (x) обязательно достигается во внутренней точке x отрезка [a, b], а по теореме Ферма имеем, что f '(x) = 0.

Теорема доказана.

Геометрический смысл теоремы Ролля: при выполнении условий теоремы внутри отрезка [a, b] обязательно найдется хотя бы одна точка x, такая, что касательная к графику f (x) в точке (x, f (x)) ïï Ox (см. рисунок).

Заметим, что все условия теоремы существенны.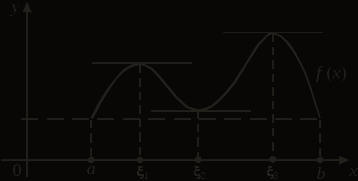


Пример 3. f (x) = çх÷, х Î [-1; 1]. f (-1) = f (1) = 1.

В точке х = 0 нарушено условие дифференцируемости. Следовательно, теорема Ролля не применяется – ни в одной точке отрезка [–1; 1] производная в нуль не обращается.

Пример 4.

Для данной функции f(0) = f(1) = 0, но ни в одной точке интервала

(0; 1) производная не равна 0, так как теорема Ролля не выполняется – функция не является непрерывной на [0; 1].

Огюстен Коши (1789–1857) – французский математик, член Парижской академии наук, почетный член Петербургской и многих других академий. Труды Коши относятся к математическому анализу, дифференциальным уравнениям, алгебре, геометрии и другим математическим наукам.

Теорема Коши. Пусть функции f (х) и g(х) непрерывны на отрезке

[a, b] и дифференцируемы на интервале (a, b), причем g'(х) ¹ 0, œх Î (a, b). Тогда на (a, b) найдется точка x, такая, что
. (1)
Доказательство.

Рассмотрим вспомогательную функцию Функция F(х) непрерывна на [a, b], дифференцируема на (a, b), причем F(а) = F(b) = 0. Следовательно, по теореме Ролля на (a, b) существует точка x, такая, что F'(x) = 0:


Следовательно:
.
Теорема доказана.

Жозеф Луи Лагранж (1736–1813) – французский математик и механик, почетный член Парижской и Петербургской академий. Ему принадлежат выдающиеся исследования по математическому анализу, по различным вопросам дифференциальных уравнений, по алгебре и теории чисел, механике, астрономии. Лагранж впервые ввел в рассмотрение тройные интегралы, предложил обозначения для производной (y', f '(x)).

Теорема Лагранжа. Пусть функция f(х) непрерывна на [a, b], дифференцируема на интервале (a, b). Тогда на (a, b) найдется точка x, такая, что


(2)
Доказательство.

Из формулы (1) при g(x) = x получаем формулу (2).

Теорема доказана.

Равенство (2) называют формулой конечных приращений или формулой Лагранжа о среднем.

Геометрический смысл теоремы Лагранжа.

При выполнении условий теоремы внутри отрезка [a, b] обязательно найдется хотя бы одна точка x, такая, что касательная к графику функции f (x) в точке (x, f (x)) параллельна секущей, проходящей через точки А (а, f (а)) и В (b, f(b)) (см. рисунок).

Рассмотрим следствия из теоремы Лагранжа:

1. (условие постоянства функции на отрезке). Пусть функция f (x) непрерывна на [a, b], дифференцируема на (a, b). Если f '(x) = 0, œх Î (a, b), то функция f (x) постоянна на [a, b].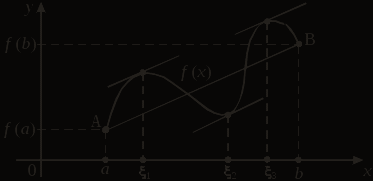


2. Пусть функции f (x) и g(х) непрерывны на отрезке [a, b], дифференцируемы на интервале (a, b), f '(x) = g'(х), œх Î (a, b). Тогда f (x) = g(х) + С, где С = const.

3. (условие монотонности функции). Пусть функция f(x) непрерывна на отрезке [a, b], дифференцируемая на интервале (a, b). Тогда, если f '(x) > 0, œх Î (a, b), то f (x) строго монотонно возрастает на (a, b). Если же f '(x) < 0,

œх Î (a, b), то f (x) строго монотонно убывает на (a, b).

2. ИССЛЕДОВАНИЕ ФУНКЦИЙ
2.1 Достаточные условия экстремума функции
В лекции 1 мы рассмотрели основные теоремы математического анализа, которые широко используются при исследовании функции, построении ее графика.

По теореме Ферма: из дифференцируемости функции f (x) в точке локального экстремума х₀ следует, что f '(x₀) = 0. Данное условие является необходимым условием существования в точке локального экстремума, то есть если в точке х₀ – экстремум функции f (x) и в этой точке существует производная, то f '(x₀) = 0. Точки х₀, в которых f '(x₀) = 0, называются стационарными точками функции. Заметим, что равенство нулю производной

в точке не является достаточным для существования локального экстремума в этой точке.

Пример 1. у = х³, у' = 3х², у'(0) = 0, но

в точке х₀ = 0 нет экстремума.

Точками, подозрительными на экстремум функции f (x) на интервале (a, b), являются точки, в которых производная существует и равна 0 либо она не существует или равна бесконечности. На рисунках функции имеют минимум в точке х₀ = 0: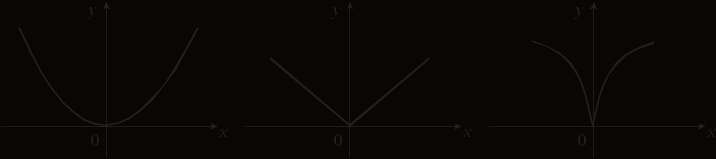


f '(0) = 0 f '(0) $ f '(0) = ¥
Рассмотрим достаточные условия существования в точке локального экстремума, которые позволят ответить на вопрос: «Есть ли в точке экстремум и какой именно – минимум или максимум?».

Теорема 1 (первое достаточное условие экстремума). Пусть непрерывная функция f (x) дифференцируема в некоторой проколотой окрестности U(x₀) точки х₀ (проколотая окрестность означает, что сама точка х₀ выбрасывается из окрестности) и непрерывна в точке х₀. Тогда:

1) если (1)

то в точке х₀ – локальный максимум;

2) если (2)

то в точке х₀ – локальный минимум.