реф. РЕФЕРАТ9. Исследование функций содержание основные теоремы дифференциального исчисления 1 Локальные экстремумы функции
 Скачать 0.94 Mb.
|
|
Доказательство. Из неравенств (1) и следствия 3 теоремы Лагранжа (о монотонности функции) следует, что при х < х0 функция не убывает, а при х > х0 функция не возрастает, то есть  (3)Следовательно, из (3) получаем, что в точке х0 функция имеет локальный максимум. Аналогично можно рассмотреть неравенства (2) для локального минимума: f (x) f (x) f '(х) ³ 0 f '(х) £ 0 f '(х) £ 0 f '(х) ³ 0 Теорема доказана. Пример 2. Исследовать на монотонность и локальный экстремум функцию  с помощью производной первогопорядка. Решение. Найдем стационарные точки функции:  Þ х2 –1 = 0 Þ х1 = –1, х2 = 1. Заметим, что данная функция не определена в точке х = 0. Следовательно:
max min То есть функция возрастает на интервалах (–¥; –1) и (1; +¥), убывает на интервалах (–1; 0), (0; 1), имеет локальный максимум в точке х1 = –1, равный уmax (–1) = –2; имеет локальный минимум в точке х2 = 1, уmin (1) = 2. Теорема 2 (второе достаточное условие экстремума). Пусть функция f (x) дважды непрерывно-дифференцируема. Если х0 – стационарная точка (f ' (х0) = 0), в которой f '' (х0) > 0, то в точке х0 функция имеет локальный минимум. Если же f '' (х0) < 0, то в точке х0 функция имеет локальный максимум. Доказательство. Пусть для определенности f '' (х0) > 0. Тогда  Следовательно: при х < х0, f ' (х) < 0, при х > х0, f ' (х) > 0. Поэтому по теореме 1 в точке х0 функция имеет локальный минимум. Теорема доказана. Пример 3. Исследовать на экстремум функцию с помощью второй производной.Решение. В примере 2 для данной функции мы нашли первую производную  и стационарные точки х1 = –1, х2 = 1.Найдем вторую производную данной функции:  Найдем значения второй производной в стационарных точках.  Þ в точке х1 = –1 функция имеет локальный максимум; Þ в точке х2 = 1 функция имеет локальный минимум (по теореме 2).Заметим, что теорема 1 более универсальна. Теорема 2 позволяет проанализировать на экстремум лишь точки, в которых первая производная равна нулю, в то время как теорема 1 рассматривает три случая: равенство производной нулю, производная не существует, равна бесконечности в подозрительных на экстремум точках. 2.2 Исследование функций на выпуклость и вогнутость. Точка перегиба Пусть функция f (х) задана на интервале (a, b) и х1, х2 – любые различные точки этого интервала. Через точки А (х1, f (х1)) и В (х2, f (х2)) графика функции f (х) проведем прямую, отрезок АВ которой называется хордой. Уравнение этой прямой запишем в виде у = у(х). Функция f (х) называется выпуклой вниз на интервале (a, b), если для любых точек х1, х2 Î (a, b), а £ х1 < х2 £ b, хорда АВ лежит не ниже графика этой функции, т. е. если f (х) £ у (х), œ х Î [х1, х2] Ì (a, b): 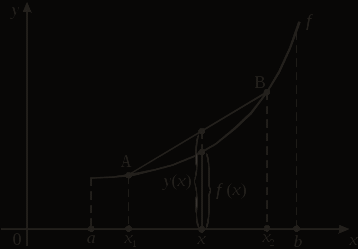 Заметим, что выпуклую вниз функцию иногда называют вогнутой функцией. Аналогично определяется выпуклость функции вверх. Функция f (х) называется выпуклой вверх на интервале (a, b), если для любых точек х1, х2 Î (a, b), а £ х1 < х2 £ b, хорда АВ лежит не выше графика этой функции, т. е. если f (х) ³ у (х), œ х Î [х1, х2] Ì (a, b): 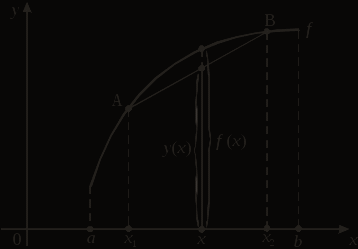 Теорема 3 (достаточное условие выпуклости). Если f (х) – дважды непрерывно дифференцируема на интервале (a, b) и 1) f ''(х) > 0, œ х Î (a, b), то на (a, b) функция f (х) выпукла вниз; 2) f ''(х) < 0, œ х Î (a, b), то на (a, b) функция f (х) выпукла вверх. Точка х0 называется точкой перегиба функции f (х), если $ d – окрест-ность точки х0, что для всех х Î (х0 – d, х0) график функции находится с одной стороны касательной, а для всех х Î (х0, х0 + d) – с другой стороны каса-тельной, проведенной к графику функции f (х) в точке х0, то есть точка х0 – точка перегиба функции f (х), если при переходе через точку х0 функция f (х) меняет характер выпуклости: х0 – d х0 х0 + d Теорема 4 (необходимое условие существования точки перегиба). Если функция f (х) имеет непрерывную в точке х0 производную f '' и х0 – точка перегиба, то f '' (х0) = 0. Доказательство. Если бы f '' (х0) < 0 или f '' (х0) > 0, то по теореме 3 в точке х0 функция f (х) была бы выпукла вверх или вниз. Следовательно, f ''(х0) = 0. Теорема доказана. Теорема 5 (достаточное условие перегиба). Если функция f (х) дважды непрерывно дифференцируема в окрестности точки х0 и при переходе через точку х0 производная f ''(х) меняет знак, то точка х0 является точкой перегиба функции f (х). Пример 4. Исследовать на выпуклость и найти точки перегиба функции у = х3. Решение. у' = 3х2, у'' = 6х = 0 Þ х0 = 0 – точка, подозрительная на перегиб. В точке х0 = 0 функция у = х3 имеет перегиб:
Пример 5. Исследовать на выпуклость и найти точки перегиба функции .Решение. В примере 3 мы уже находили вторую производную данной функции  . Так как  то точек подозрительных на перегиб нет. Рассмотрим промежутки выпуклости:
2.3 Асимптоты графика функции Асимптотой будем называть прямую, к которой график функции неограниченно близко приближается. Различают вертикальные и наклонные асимптоты. Прямая х = х0 называется вертикальной асимптотой графика функции f (х), если хотя бы один из пределов f (х0 – 0) или f (х0 + 0) равен бесконечности. Пример 6. Найти вертикальные асимптоты функций: а)  б)  в)  Решение. Вертикальными асимптотами функций будут прямые х = х0, где х0 – точки, в которых функция не определена. а) х = 3 – вертикальная асимптота функции  . Действительно,  ;б) х = 2, х = – 4 – вертикальные асимптоты функции  . Действительно,  , ;в) х = 0 – вертикальная асимптота функции Действительно,  .Прямая у = kx + b называется наклонной асимптотой графика непрерывной функции f (х) при х ® +¥ или х ® – ¥, если f (х) = kx + b + α(х),  , то есть если наклонная асимптота для графика функции f (х) существует, то разность ординат функции f (х) и прямой у = kx + b в точке х стремится к 0 при х ® +¥ или при х ® – ¥. |