Курсовая работа. Исследование искажений сигналов на выходе фильтра нижних частот
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
2. Определение передаточной функции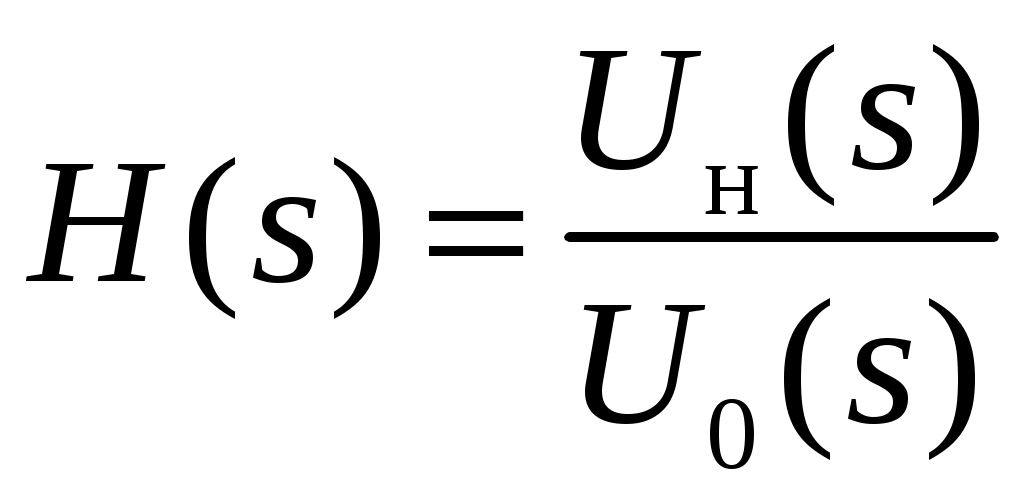 Для нахождения H(s) применим метод пропорциональных величин. 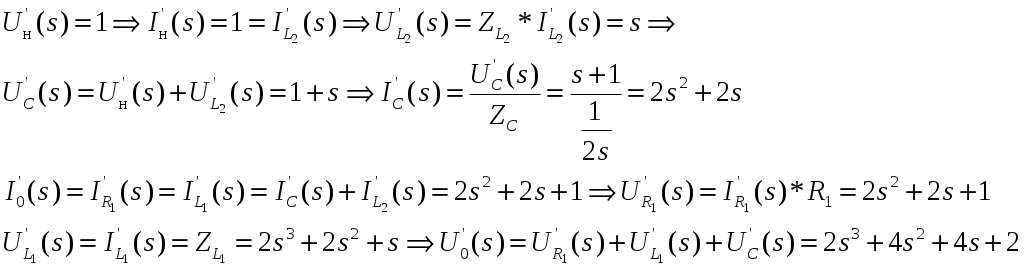 Таким образом, Таким образом, 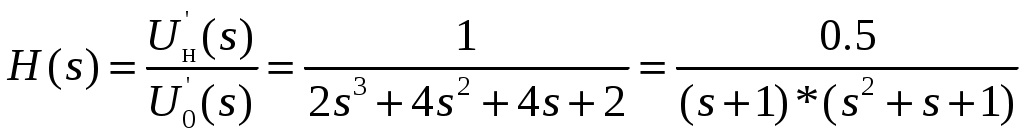 Полюсы H(s), т.е. корни характеристического полинома цепи, равны: S1 = -1; S2,3 = -0.5 ± ј0.866. Их расположение показано на рис. 4.  Рис. 4 Проконтролируем функцию H(s). H(0) = 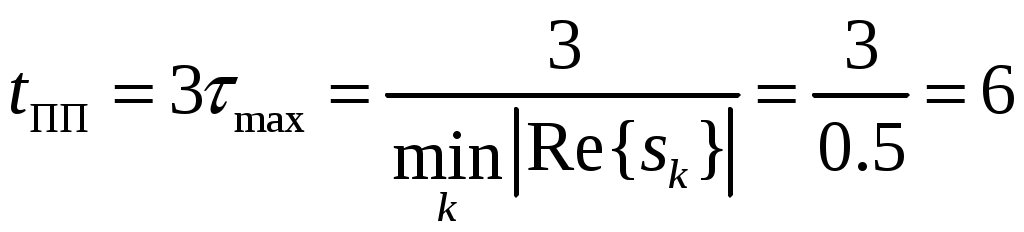 3. Расчет частотных характеристик цепи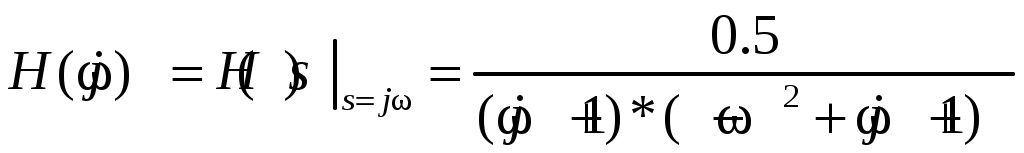 АЧХ: 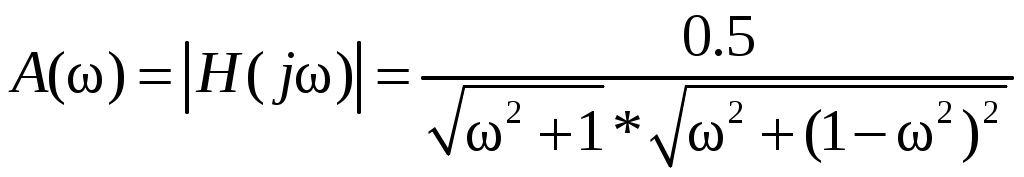 ФЧХ: 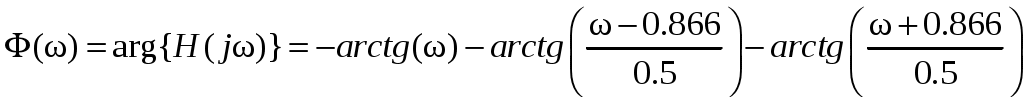 Графики АЧХ, ФЧХ и АФК приведены на рис. 5, а, б, в. Определим полосу пропускания: 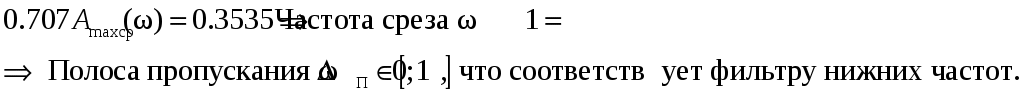 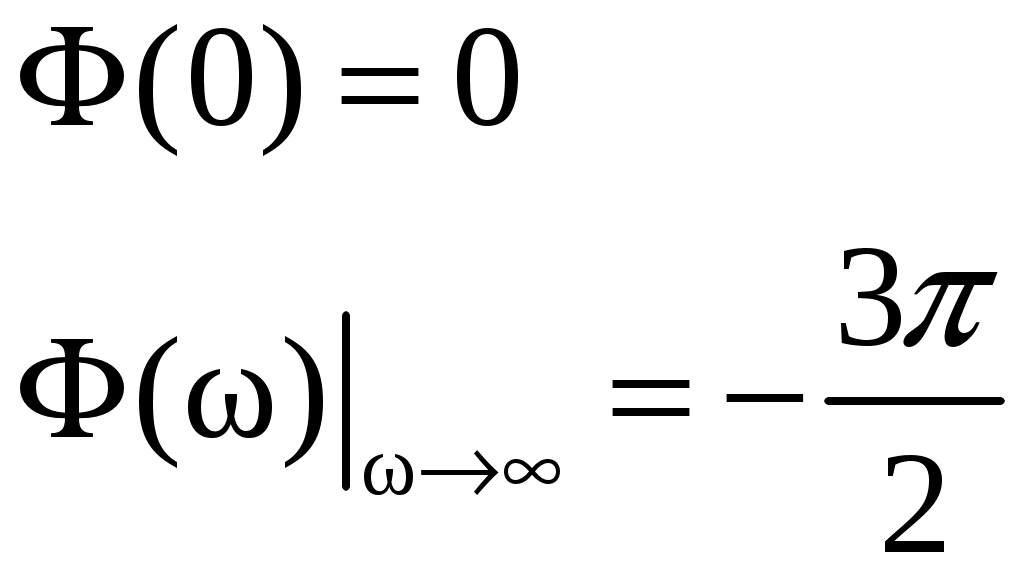 Оценим время запаздывания по наклону графика ФЧХ в области низких частот: 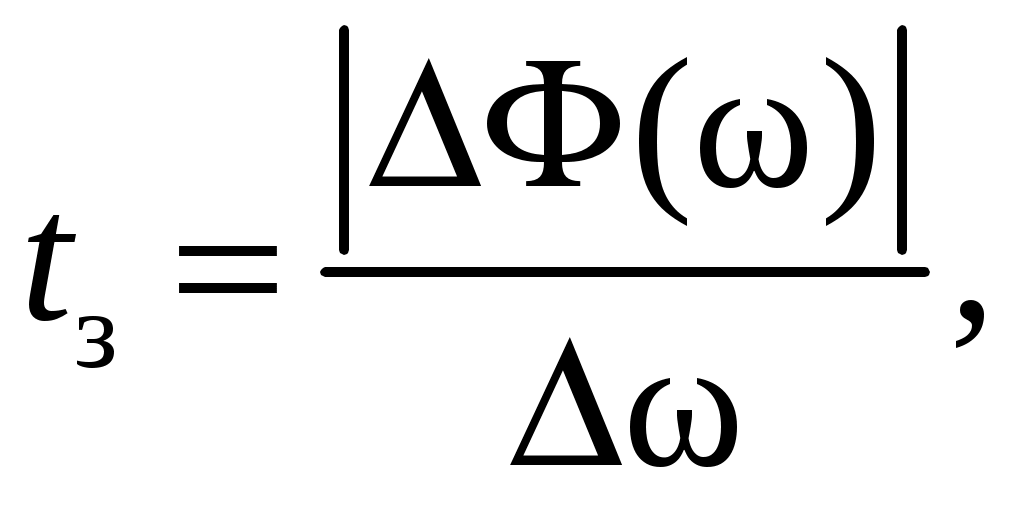 где – приращение фазы, рад; Δω – приращение частоты в области низких частот. Для ФНЧ можно также использовать формулу tз 0 . Таким образом, tз 2 с. 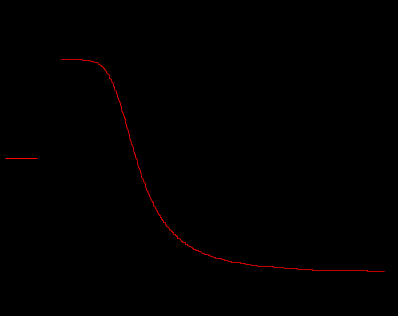 Рис. 5, а 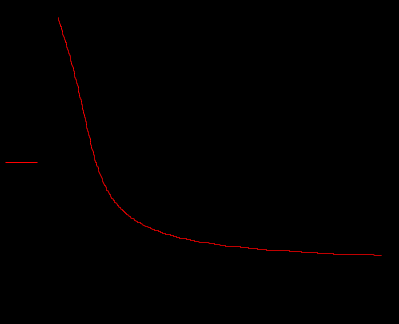 Рис. 5, б 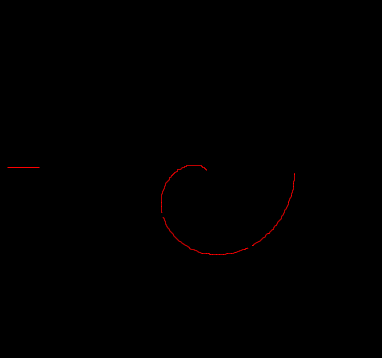 Рис. 5, в 4. Составление уравнений состояния цепиНа рис 6, а приведена исходная схема, на рис 6, б приведена схема замещения (L – элементы заменяются на источники тока R1 L1 L2 R1 iL1(t) iL2(t) 1 2 3 4 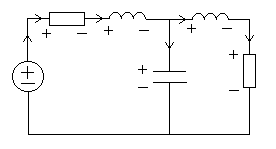 u1 C R2 u1 R2 iC(t) uC(t) 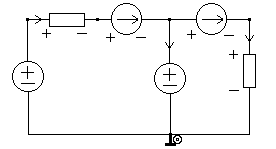 Рис. 6, а Рис. 6, б По МУН: 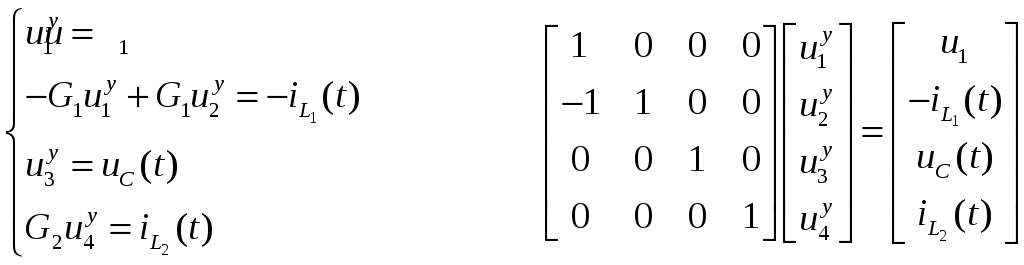 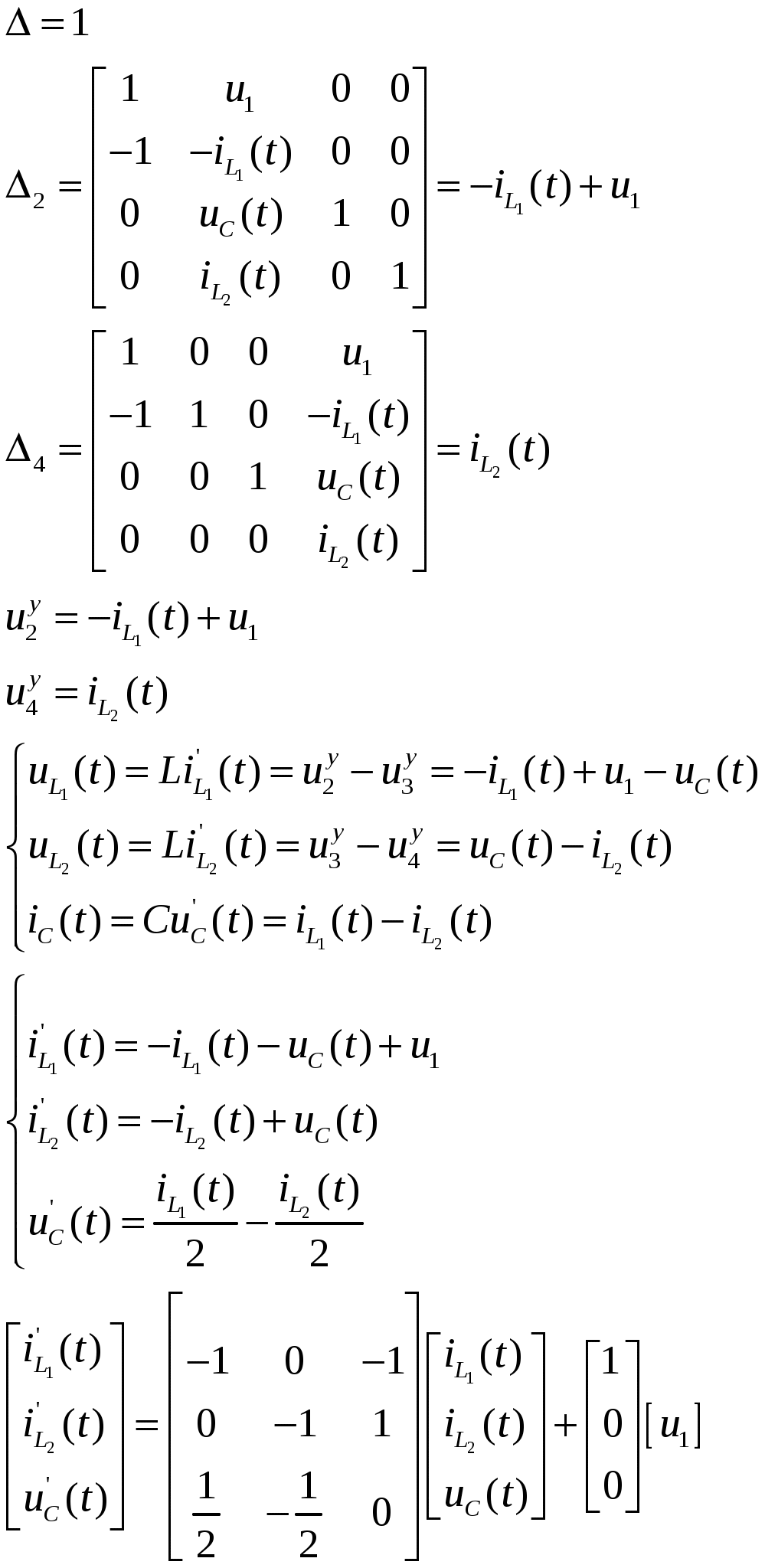 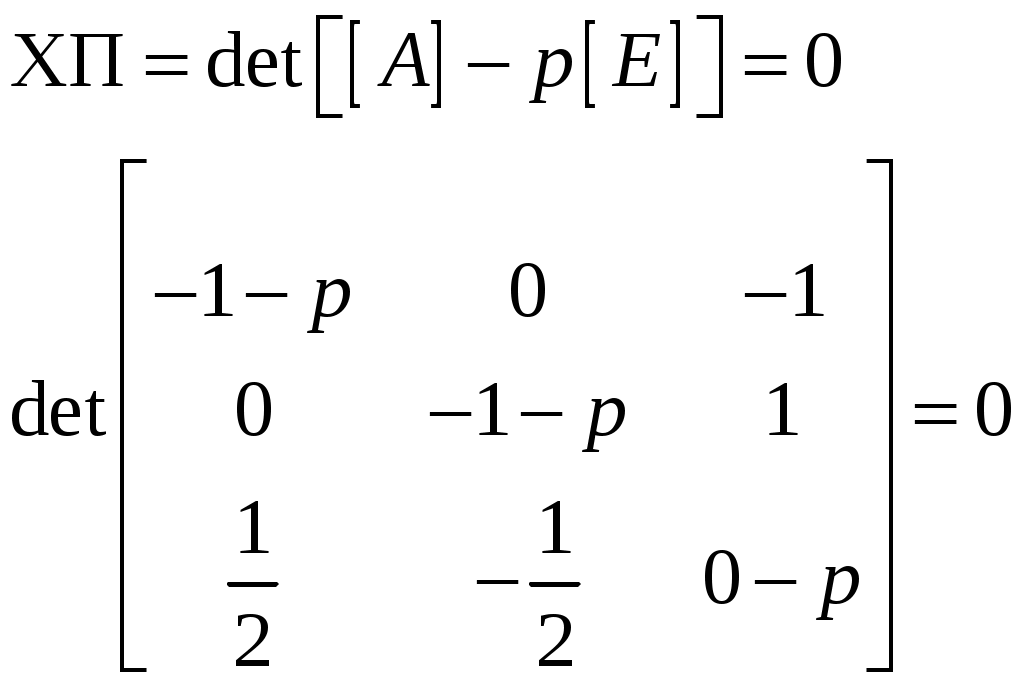 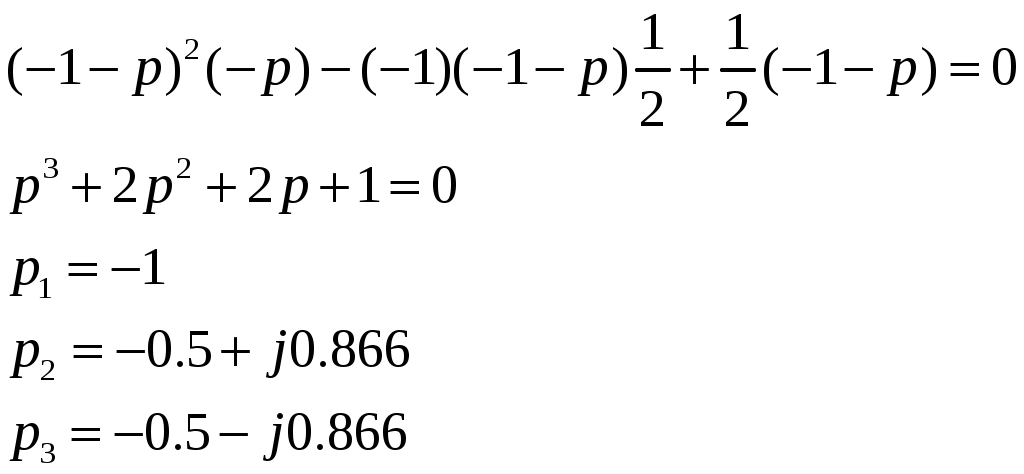 |
