Исследование кривошипношатунного механизма (рис. 1). Для этого
 Скачать 1.3 Mb.
|
|
Задание: Выполнить исследование кривошипно-шатунного механизма (рис.1). Для этого: 1. Провести структурный, геометрический, кинематический анализ и силовой расчет механизма и определить уравновешивающий момент ТУР, Н*м; 2. Выполнить прочностной расчет детали механизма.  Рис.1. Схема механизма Исходные данные :
1. Общие сведения Машина - это устройство, выполняющее механическое движение для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека. Обычно машина состоит из источника движения - двигателя (внутреннего сгорания, электрического, ветряного, водяного и пр.), преобразователя и передатчика движения - механизма, потребителя движения - исполнительного органа, а также других частей. Механизм - это система тел, предназначенная для преобразования движения одного или нескольких твердых тел в требуемые движения других твердых тел. Твердое тело, входящее в состав механизма, неподвижное или перемещающееся относительно других тел, называется его звеном. Звено может состоять из одной или нескольких жестко скрепленных друг с другом деталей. Звено, принимаемое за неподвижное, называется стойкой. Входным называется звено, которому сообщается движение двигателя, преобразуемое механизмом в требуемые движения других звеньев. В машине входное звено образуется соответствующим телом механизма и скрепленной с ним подвижной частью двигателя. Выходное звено - звено, совершающие движение, для выполнения которого предназначен механизм. В машине это звено образуется соответствующим телом механизма и скрепленным с ним исполнительным органом. Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой. Кинематическая пара с одной степенью свободы в относительном движении её звеньев - это одноподвижная пара. Пары могут иметь от одной до пяти степеней свободы (подвижностей). Система звеньев, связанных между собой кинематическими парами называется кинематической цепью. Механизм - это замкнутая кинематическая цепь с одной стойкой и обычно с одной степенью свободы (подвижностью, равной единице). Чаще всего замыкающим звеном является стойка. Схема механизма, указывающая стойку, подвижные звенья, виды кинематических пар и их взаимное расположение, называется структурной схемой механизма. При изображении структурных схем используют условные стандартные обозначения по ГОСТ 2.770-68. Вращающееся звено рычажного механизма, которое может совершать полный оборот вокруг неподвижной оси, называется кривошипом. Вращающееся звено рычажного механизма, которое может совершать только неполный оборот вокруг неподвижной оси, называется коромыслом. Если звено образует кинематические пары только с подвижными звеньями, то такое звено называется шатуном. Звено, которое образует поступательную пару со стойкой, называется ползуном. Если такое звено образует поступательную пару с поворотным звеном - кулисой, то оно называется «камень». 2. Структурный анализ механизма При структурном анализе определяют количество подвижных звеньев п и степень подвижности W механизма, вид его начального механизма и структурных групп нулевой подвижности, в частности, групп Ассура. Степень подвижности механизма определяют по формуле Чебышева:  ,где  - количество подвижных звеньев; – количество кинематических пар V класса; – количество кинематических пар IV класса .3. Геометрический анализ механизма При геометрическом анализе рычажного механизма определяют ход ведомого звена. Анализ ведут по заданной кинематической схеме. Результаты метрического анализа следует проиллюстрировать несколькими планами положений механизма, построенными при неизменном положении стоек и последовательно изменяющихся положениях подвижных звеньев. Эти планы позволят найти ход выходного звена. Вначале выберем масштабный коэффициент l, плана положений:  ,где ОА – реальная длина кривошипа в метрах, а (ОА) – длина отрезка на чертеже в миллиметрах (принимаем (ОА)=40 мм). Вначале рекомендуется в тонких линиях построить два крайних положения механизма. При известных положениях стоек и неизменных длинах рычагов вначале тонкими линиями обозначают траектории движения некоторых точек звеньев: шарнир на конце кривошипа перемещается по окружности с центром в точке О с радиусом, равным длине кривошипа r; шарнир на конце коромысла - по соответствующей дуге окружности с центром во втором его шарнире на стойке; любая точка ползуна (поршня) перемещается по прямой, параллельной соответствующей направляющей или совпадающей с ней. Далее вычерчивание ведется методом засечек раствором циркуля, равным длине шатуна. Начало шатуна назначается в одной из точек и известной траектории начала его движения. Конец шатуна «засекается» на траектории его движения (на прямой линии). 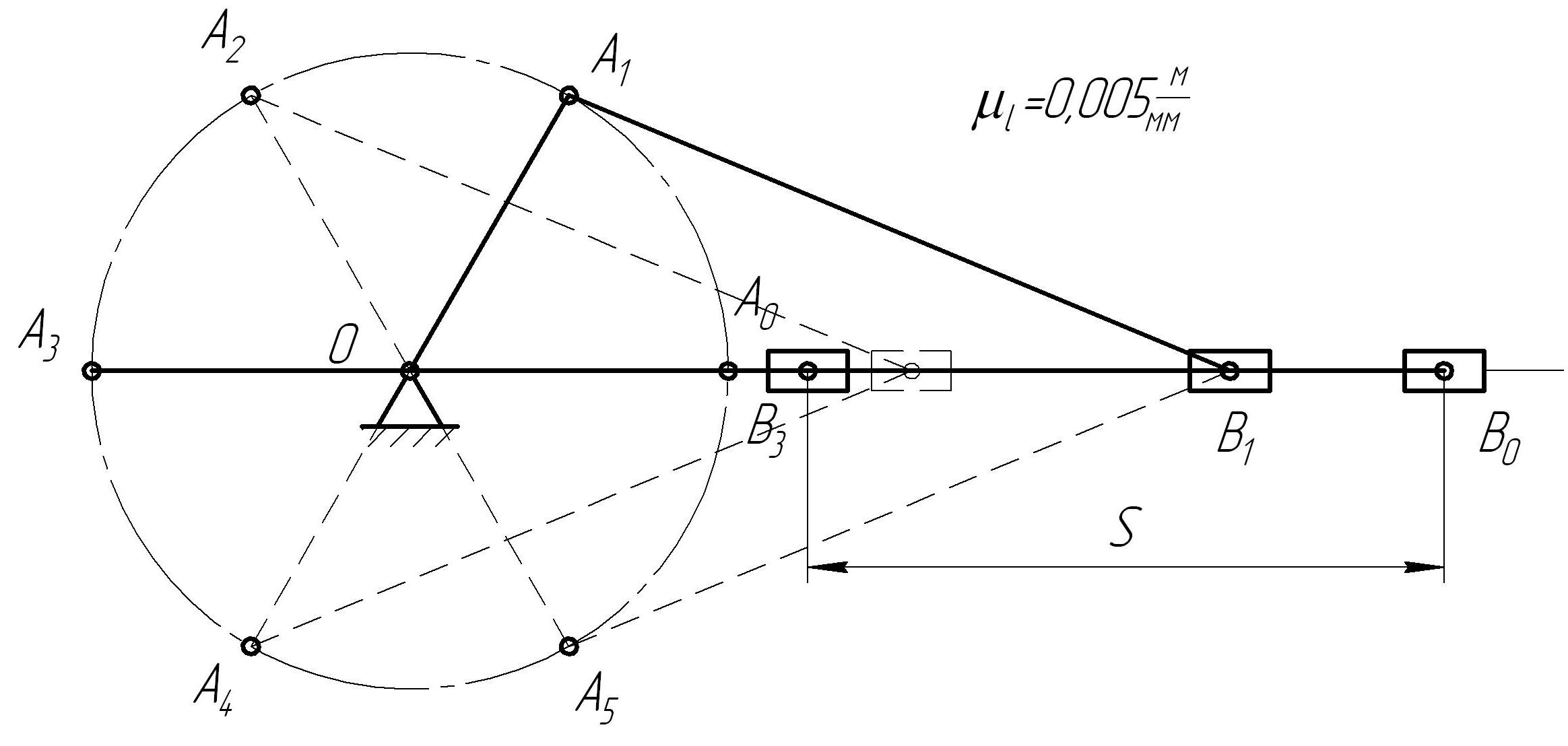 Рис.2. План положений механизма (S– ход поршня). Кривошипы, шатуны и ползуны во втором, четвертом и пятом положениях условно показаны пунктиром. Разность крайних положений есть ход Sвыходного звена. За один оборот кривошипа оно сместится из одного крайнего положения в другое и вернется назад, пройдя путь 2S.  .4. Кинематический анализ механизма При кинематическом анализе находят мгновенные значения угловых скоростей ωi звеньев механизма, мгновенные значения угловых ускорений εi рычагов; находят также мгновенные Vi значения поступательных скоростей и ускорений аi характерных точек звеньев рычажного механизма - центров шарниров и центров масс Si звеньев. Анализ ведут по имеющейся кинематической схеме и заданной угловой скорости кривошипа ωк. Результаты кинематического анализа следует свести в таблицы 1 и 2, и проиллюстрировать планами скоростей механизма, а также планами ускорений механизма. Скорость и ускорение точки О стойки в любом пространственном положении равны нулю. Угловую скорость вращения первого подвижного звена ω1 можно определить, если задана частота вращения кривошипа коленчатого вала nк, об/мин:  (1)Угловая скорость вращения ω1 будет одинаковой в любом пространственном положении. Вектор мгновенной скорости т. А в любом пространственном положении  направлен перпендикулярно кривошипу в сторону вращения кривошипа ОА.Модуль вектора скорости VА, м/с определяется по формуле:  (2)Вектор скорости мгновенной точки В является векторной суммой вектора мгновенной скорости точки А и скорости относительного движения шатуна АВ относительно точки А:  (3)Направление вектора  мгновенной скорости точки В в любом пространственном положении совпадает с направлением движения точки В – прямой линией.Линия действия вектора  перпендикулярна шатуну АВ, а направление вектора пока не известно.Для нахождения неизвестных пока векторов  удобно использовать графо-аналитический метод. Он заключается в построении планов скоростей конечных точек звеньев механизма в заданных пространственных положениях.Для начала следует выбрать масштаб плана скоростей μV:  .Построение начинается из произвольной точки pv – полюса плана скоростей. Из нее проводится отрезок, длина которого соответствует длине вектора , в масштабе μV , а направление перпендикулярно кривошипу ОА. Конец этого отрезка обозначается точка а.Затем, через точку а проводится линия действия вектора (перпендикулярно шатуну АВ). Из полюса pv проводится линия действия вектора - прямая линия до пересечения с линией действия вектора . Точка пересечения этих двух отрезков – точка в. Результирующий вектор , по правилу сложения векторов замыкает начало вектора и конец (рис.3).Полученное построение называется планом скоростей механизма. С его помощью можно определить направление вектора 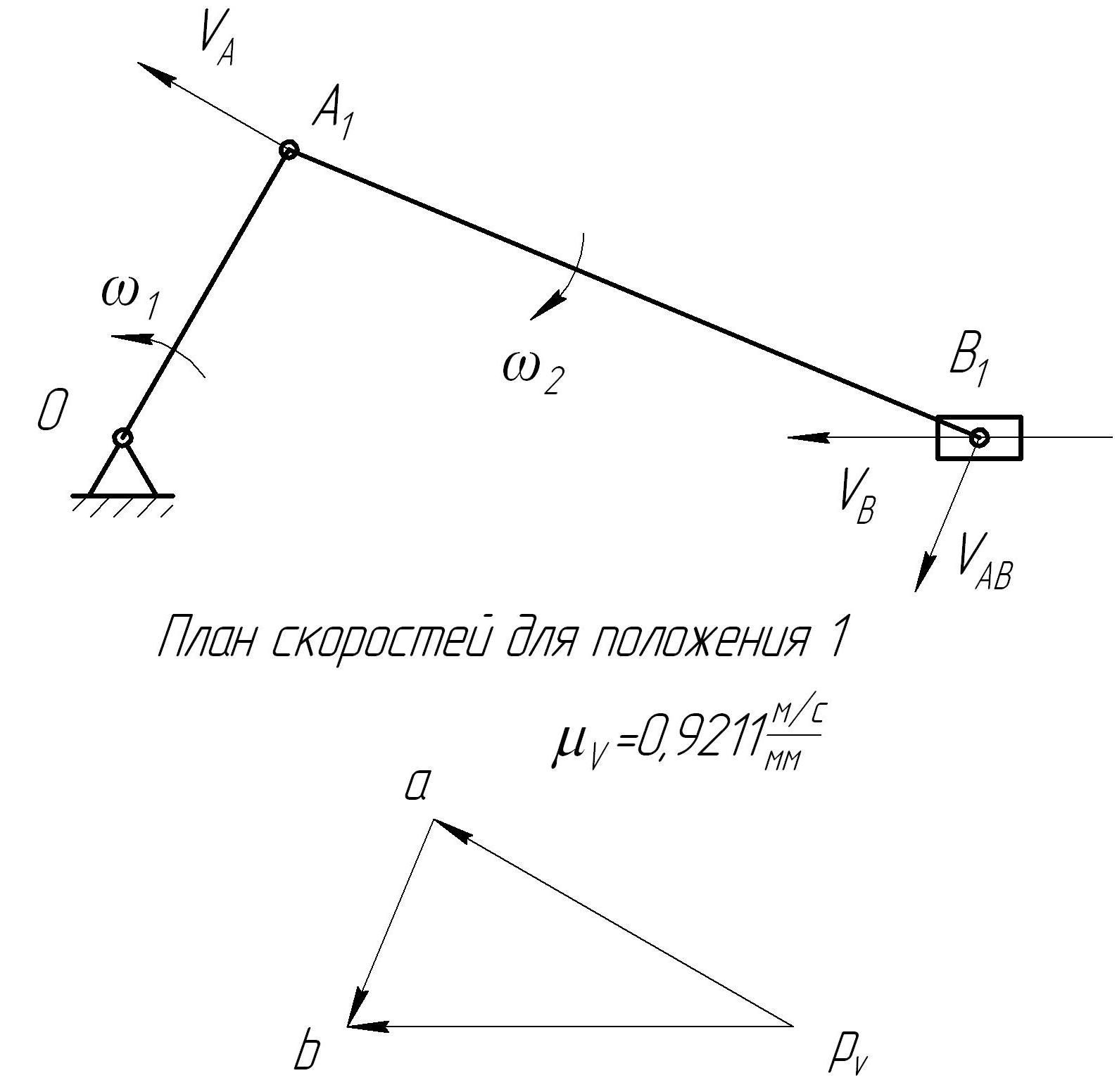. А измерив длины отрезков pvв и ав, и умножив их на масштаб μVможно вычислить мгновенные значения скоростей VB и VАВ. Рис.3. План скоростей механизма для первого пространственного положения  , .Угловая скорость вращения шатуна АВ ω2:  .Таблица 1 Результаты определения скоростей
Величина мгновенного ускорения конца кривошипа точки А определяется по формуле, м/с2:  (4)Линия действия вектора  совпадает с направлением кривошипа ОА, а направление – от точки А к точке О.Для построения плана ускорений выбирают масштаб плана скоростей μа: μа = м/с2 (реального ускорения)/мм (длины векторов на чертеже).  .В соответствии с теоремой Кориолиса, вектор ускорения точки В:  , (5)где  – вектор ускорения точки В относительно точки А; – вектор касательной (тангенциальной) составляющей ускорения точки В относительно точки А.Величина нормальной составляющей относительного ускорения определяется по формуле:  , (6)а ее вектор параллелен шатуну АВ и направлен от точки В к точке А.Про величину и направление тангенциальной составляющей относительного ускорения пока ничего сказать нельзя, но известно, что линия ее действия перпендикулярна шатуну АВ.Также нельзя пока определить величину и направление вектора ускорения точки В -  , но понятно, что линия его действия совпадает с горизонтальной прямой – траекторией движения ползуна.Построение ведется из произвольной точки pа – полюса плана ускорений. Из нее откладывается отрезок, длина которого соответствует длине вектора в масштабе μа, направление - от точки А к точке О. В конце этого отрезка ставим точку а.Из точки а плана ускорений откладываем отрезок, советующий величине вектора в масштабе μа.  .Направление отрезка от точки В к точке А, параллельно шатуну АВ. В конце отрезка ставим точку n1. Через точку n1 перпендикулярно шатуну АВ проводим линию действия вектора .Наконец, из полюса плана ускорений т.pа проводим прямую горизонтальную линию - линию действия вектора . На пересечении этой линии с линией действия вектора ставим точку в.В соответствии с векторным уравнением (5) и правилом сложения векторов расставляем стрелки, обозначающие направления отрезков – так, чтобы отрезок pав соединял начало отрезка pаа и конец отрезка n1в (рис.4). С помощью плана теперь можно измерив длины отрезков pав и n1в, и умножив их на масштаб μа,можно вычислить мгновенные значения ускорений ав, и .Т.к. кривошип ОА движется равномерно и угловая скорость его вращения ω1= const, то угловое ускорение кривошипа для всех пространственных положений равно нулю, ε1=0. Угловое ускорение шатуна для любого пространственного положения определяется по формуле, 1/с2: 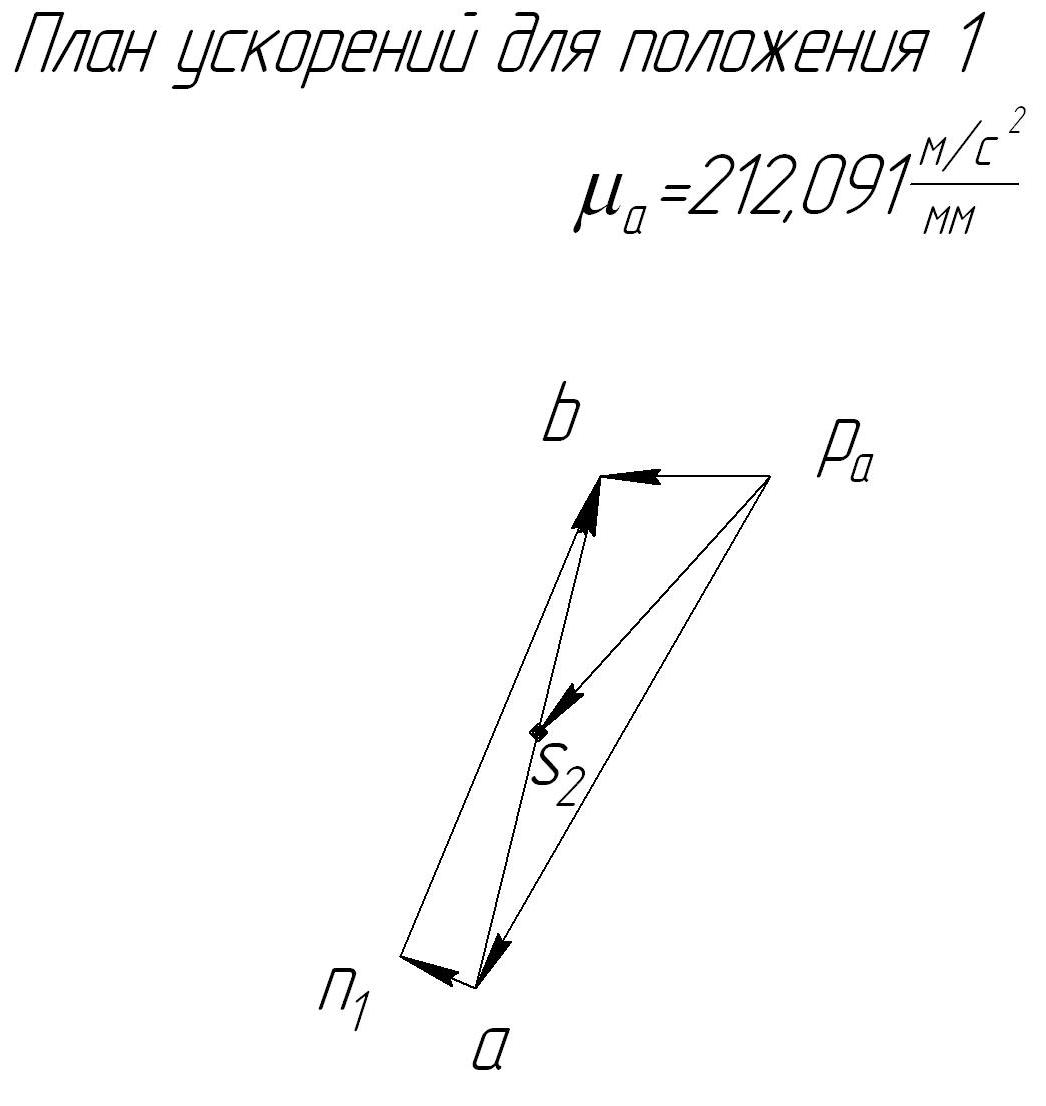  Рис.4. План ускорений механизма для первого пространственного положения Для последующего силового расчета потребуется также определить мгновенное ускорение точки S2 – середины шатуна АВ. Для этого на плане ускорений соединяем отрезком точки а и в, и на его середине отмечаем точку s2. Проводим отрезок от полюса плана ускорений точкиpа к точке s2. Длина отрезка pаs2, умноженная на масштаб μа, позволяет определить мгновенное ускорение середины шатуна  , м/с2, а длина отрезка ав, умноженная на масштаб μа, дает возможность определить мгновенное значение относительного ускорения aAB, м/с2. , , , , .Результаты определения ускорений сводим в таблицу 2. Таблица 2 Результаты определения ускорений
|