Исследование кривошипношатунного механизма (рис. 1). Для этого

• Название: Исследование кривошипношатунного механизма (рис. 1). Для этого
• Дата: 04.04.2022
• Размер: 1.3 Mb.
• Имя файла: KR.doc
• Тип: Исследование; #441891
• страница: 2 из 3

5. Силовой расчет механизма
Целью силового расчета механизма является определение уравновешивающего момента Т_УР, Н*м.

Для его определения потребуется найти мгновенные значения сил и моментов сил инерции, а также величины реакций в кинематических парах.

Исходными данными являются массы отдельных звеньев m_i, моменты инерции звеньев I_i, координаты положений центров масс звеньев и внешняя сила на ползуне Q.
5.1. Определение уравновешивающей силы F_УР кинетостатическим методом.

В соответствии с третьим законом Ньютона все тела действуют друг на друга с силами равными по модулю и противоположными по направлению. Реакции в звеньях кинематических пар (силы давления одного звена на другое в процессе передачи движения) равны по модулю и обратны по направлению. Условимся обозначать реакции R_lk, где l и k – номера звеньев кинематической пары. Очевидно, что .

Обозначим стойку цифрой 0, кривошип ОА – цифрой 1, шатун АВ – 2, ползун В – 3.

Для силового расчета используется принцип Даламбера (принцип кинетостатики), в соответствии с которым для нахождения реакции в кинематической паре необходимо к внешним силам прибавить силы инерции. Силы трения в данной работе не учитываются.

Главный вектор сил инерции звена k, Н:

(7)

где m_k – масса звена k, кг;

- ускорение центра масс звена k, м/с².

Стоит отметить, что вектор сил инерции звена направлен противоположно направлению ускорения звена.

Главный момент сил инерции звена k, Н*м:

(8)

где I_k – момент инерции звена k, относительно центральной оси кг*м²;

- угловое ускорение звена k, 1/с².

При неизвестных моментах инерции звеньев их можно определить по приблизительной формуле:

(9)

Находим координаты положений центров масс звеньев. Для кривошипа ОА и шатуна АВ – это точки, лежащие на серединах звеньев

и .

Центр масс ползуна (звена 3) совпадает с точкой В.

Для определения направления ε₂ - углового ускорения звена АВ мысленно переносим в точку В вектор (совпадающий с ним по направлению отрезок n₁в на плане ускорений). Видно, что ускорение ε₂ направлено против хода часовой стрелки относительно точки А.

Затем определяем силы инерции и моменты инерции всех звеньев.

Центр масс звена 1 (кривошипа ОА) находится на оси вращения звена, поэтому его сила инерции кривошипа равна нулю, т.е. F₁=0.

Момент сил инерции звена 1 также равен нулю, т.к. кривошип движется равномерно и его угловая скорость постоянна, т.е. ω₁= const, и М₁=0.

Для звена 2 (шатуна АВ) модуль силы инерции:

_,

а направление вектора противоположно направлению вектора .

Модуль момента сил инерции звена 2: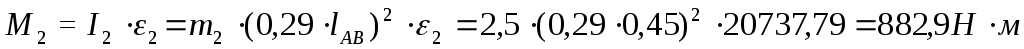

,

а направление момента - в сторону, противоположную направлению углового ускорения шатуна .

Звено 3 (ползун или поршень) совершает только поступательное движение, поэтому на него действует только сила инерции

_.

Направлена эта сила по траектории движения ползуна в противоположную сторону от направления вектора ускорения .

Силовой анализ проводят в последовательности, обратной его кинематики. Простейшей кинетостатической цепью обладающей определимостью является структурная группа Ассура.

Начинаем с последнего звена. Вычерчиваем группу, состоящую из звена 3 (ползуна), звена 2 (шатуна АВ) и стойки 0 в масштабе. В центрах масс звеньев прикладываем сначала вес звеньев 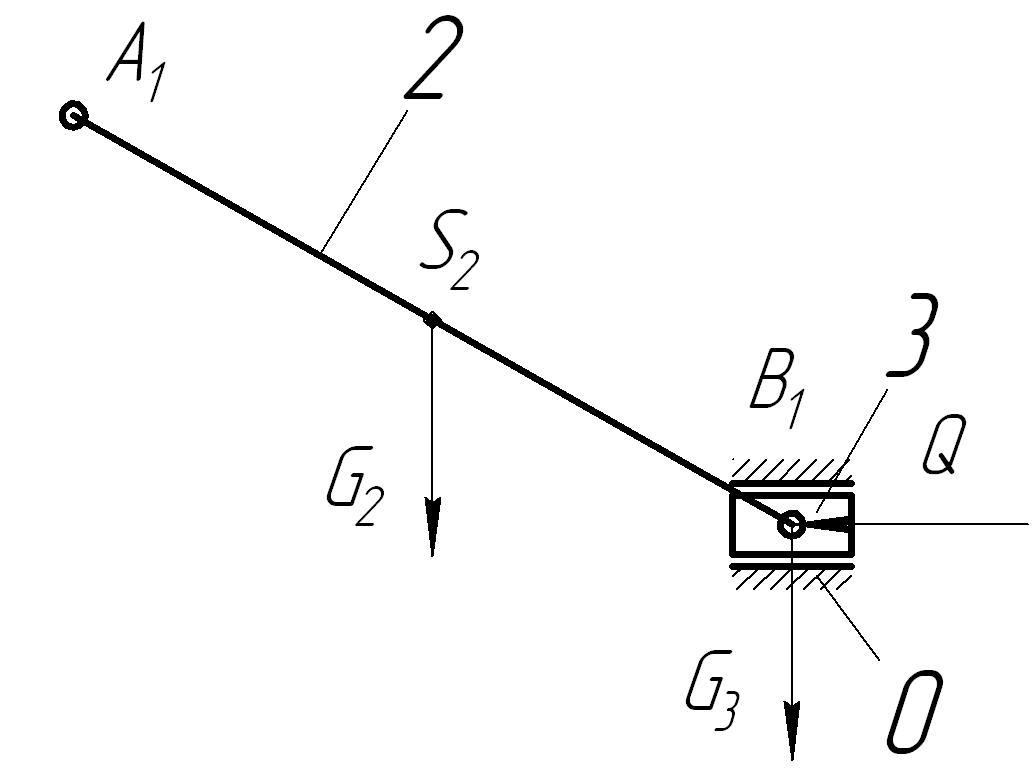и , а также заданную силу сопротивления Q (рис.5). Направление веса каждого звена - вертикально вниз, силы Q – против движения.


Рис.5. Группа Ассура с приложенными весами и силой сопротивления
Затем прикладываем инерционные нагрузки F₂, F₃ и М₂.

Последними прикладываем искомые реакции R₀₃, R₂₁ и R₂₃. Направление реакции стойки 0 на ползун 3 перпендикулярно траектории. Реакция звена 2 на звено 1 R₂₁ действует в точке А. Направление ее неизвестно, но ее можно разделить на нормальную Rⁿ₂₁ и тангенциальную R^τ₂₁ составляющие. Направление нормальной составляющейRⁿ₂₁ – параллельно звену 2, а тангенциальной R^τ₂₁ – перпендикулярно звену 2 в произвольную (предварительно) сторону.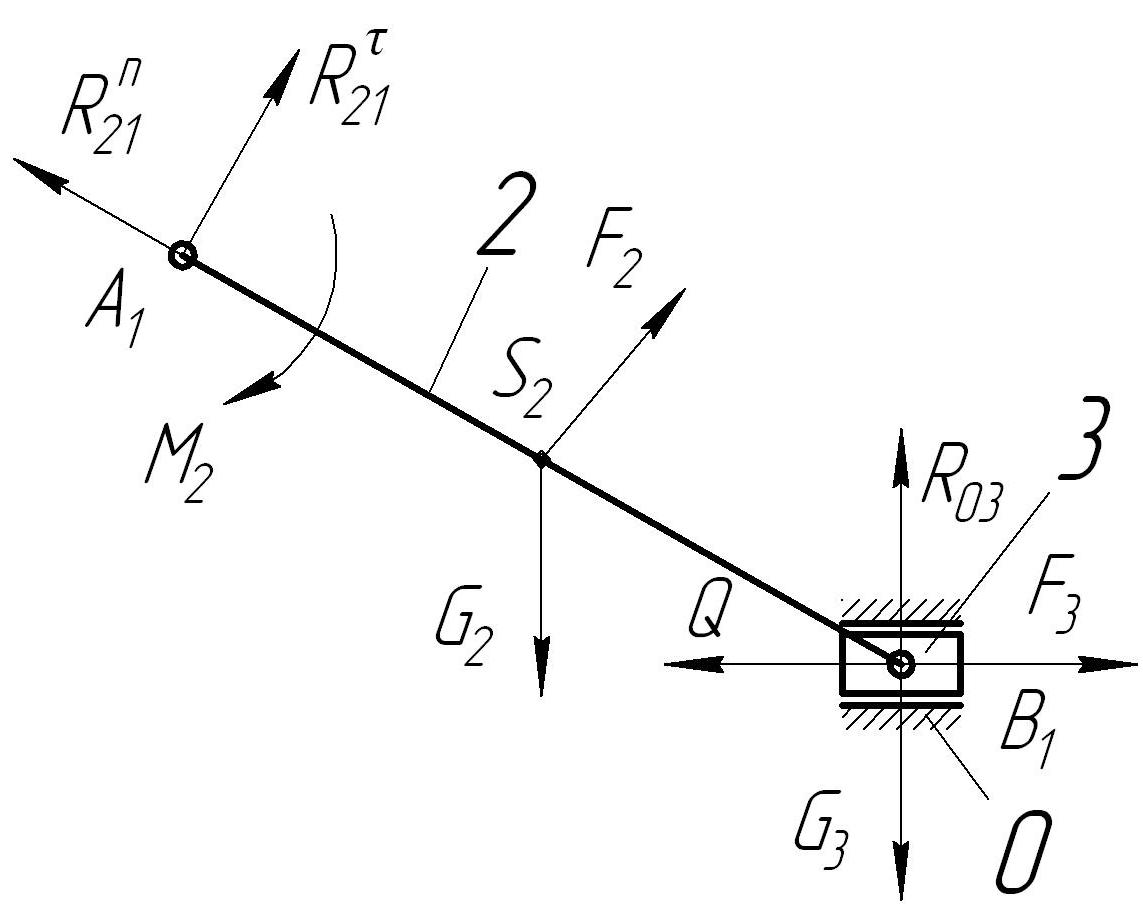




Рис.6. Группа Ассура с приложенными весами, силами и моментом инерции, и реакциями (реакция R₂₃ условно не показана).
Т.к. здесь 3 неизвестных вектора ( ), то сначала находим . Для этого составляем уравнение равновесия моментов сил, действующих относительно точки В:
(10)
Условимся, что любая сила или момент, вращающие звено по часовой стрелке, берутся с отрицательным знаком, вращающие против часовой стрелки – с положительным.

(11)

где h_G2 и h_F2 – значения плеч от точки В до линии действия векторов G₂ и F₂ (см. рис 7).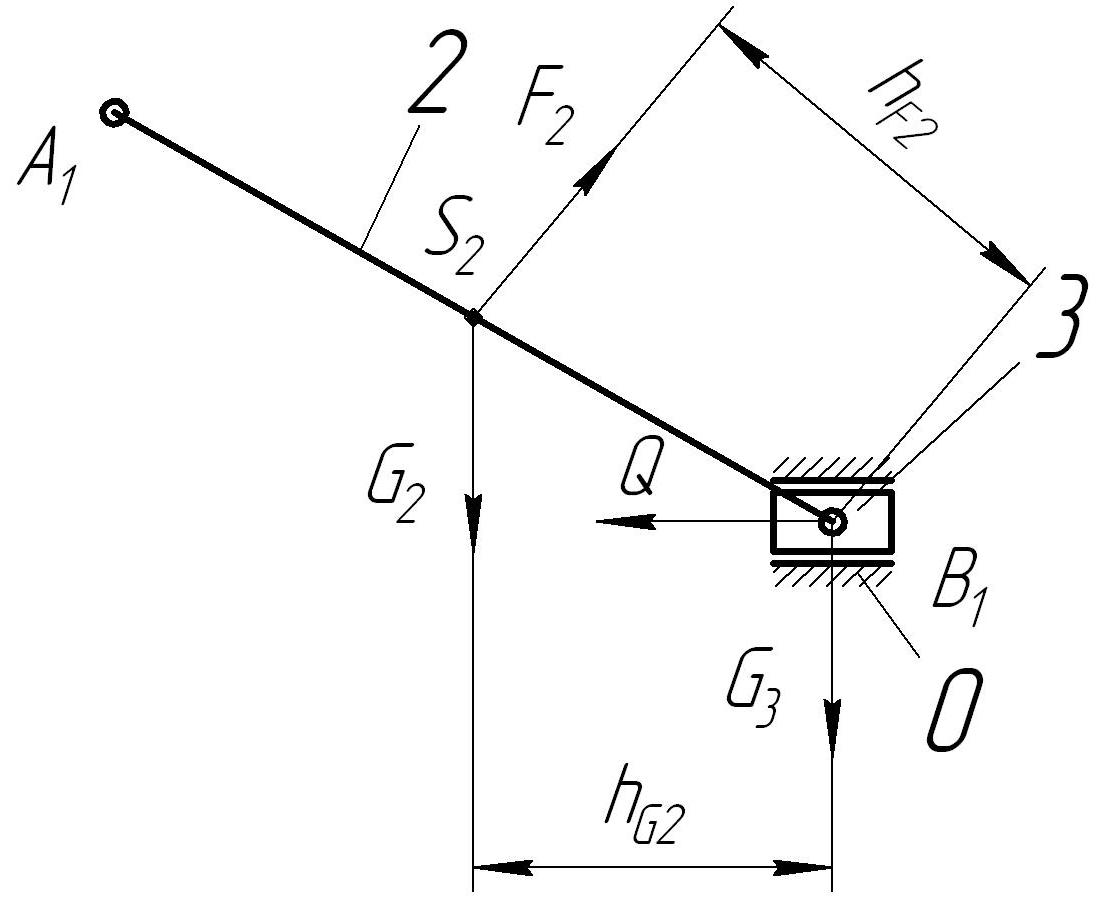

,

,



Рис.7. Пояснение к определению плеч h_G2 и h_F2
Решаем уравнение 11:



Так как значение R^τ₂₁ получилось со знаком «минус», то это означает, что предварительно выбранное направление вектора в дальнейших построениях надо поменять на противоположное.

Теперь строим план сил для первой группы. Для этого сначала записываем уравнение всех сил действующих в группе в векторной форме:

(12)

Затем выбираем масштаб плана сил μ_f (Н/мм).



Из произвольного полюса p_f откладываем последовательно в масштабе сначала вектор , затем , . Через конец вектора Q проводим вертикаль – линию действия вектора . А через начало вектора проводим линию, параллельную звену 2 (шатуну АВ). Замыкаем прямоугольник сил и находим модули и направления векторов . Модули определяются как произведение длин соответствующих отрезков на плане сил на масштаб плана μ_F.

;

;

;

;

;

;

;

.

Реакцию определяем на плане как векторную сумму и (рис.8 а).

.

Неизвестную реакцию определяем с помощью векторного уравнения:

(13)

Строим многоугольник сил (рис.8 б), измеряем длину вектора 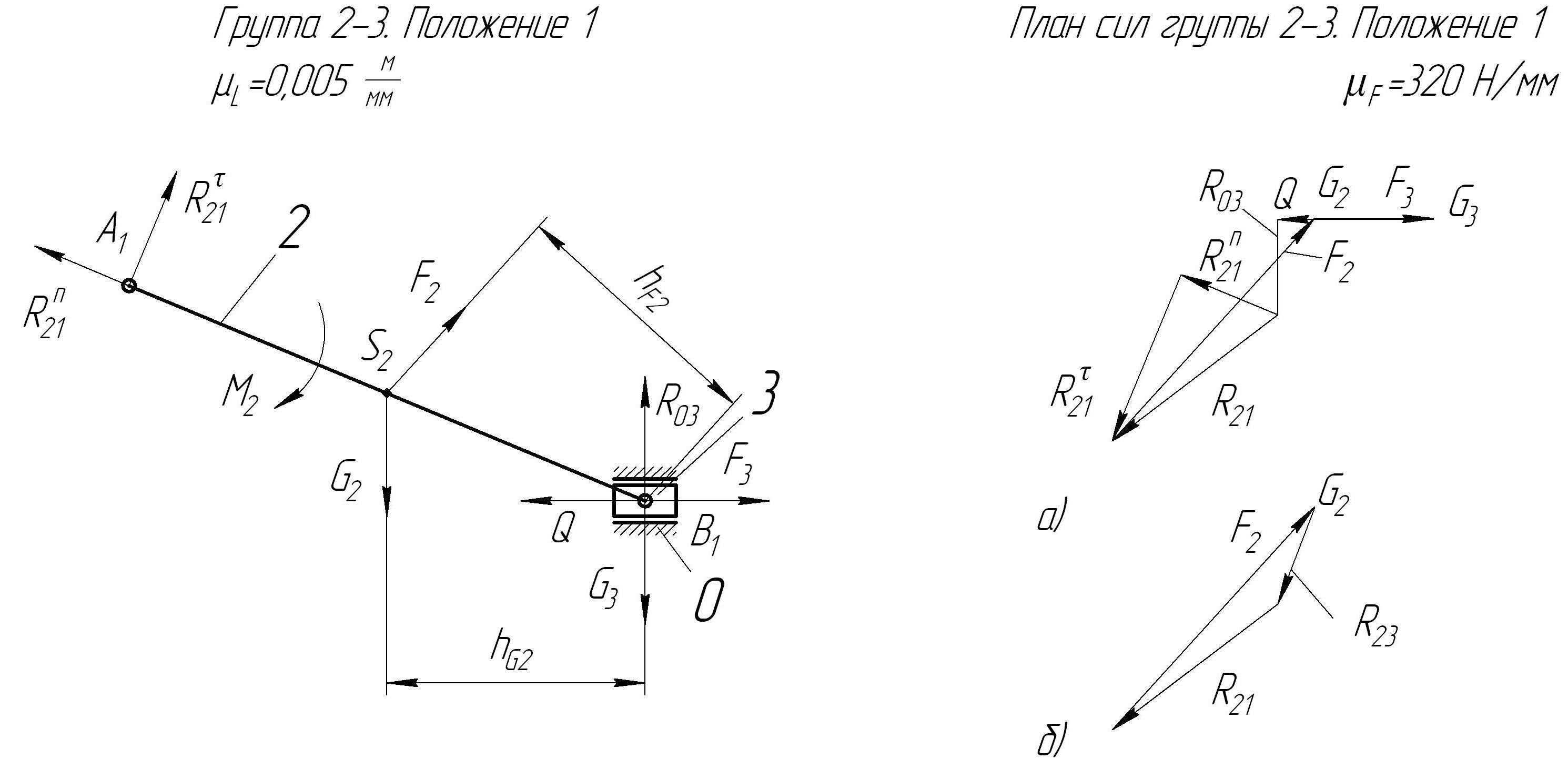, умножаем ее на масштаб, и результаты записываем в таблицу 3.

.



Рис.8. Планы сил для первой группы механизма в первом положении
Вторая группа Ассура состоит из двух звеньев: стойки 0 и кривошипа 1.

Вычерчиваем группу в том же масштабе, что и предыдущую. В точку А переносим определенную ранее реакцию R₁₂ = R₂₁, но направление вектора выбираем противоположно направлению вектора . Также в центре кривошипа наносим вес звена 1 _, а искомую реакцию от стойки на кривошип размещаем в точке O и направляем предварительно произвольно.

Записываем векторное уравнение:

(14)

Из произвольного полюса p_f откладываем векторы 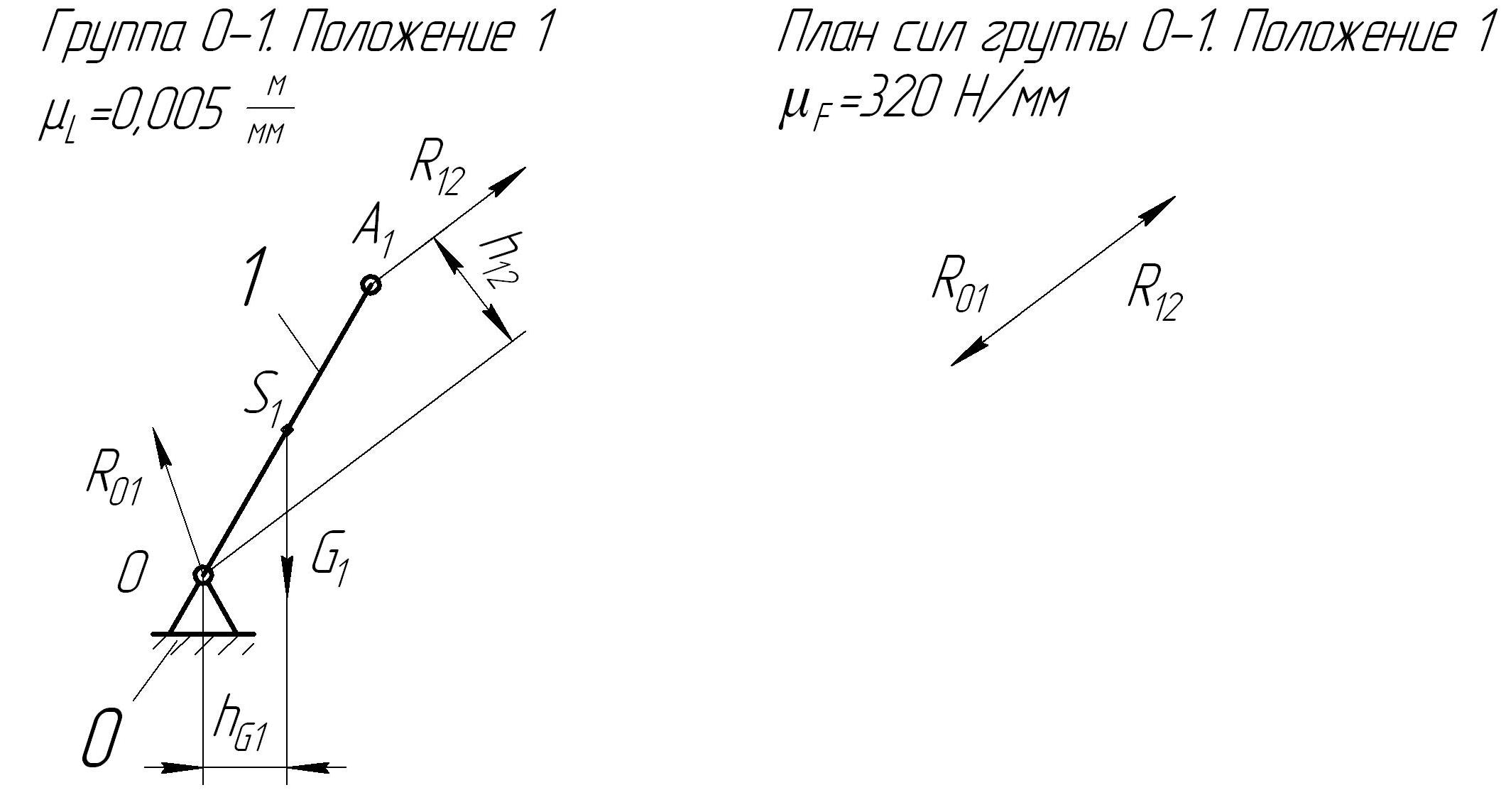и (рис.9). Вектор строится от начала к концу .

;

.




Рис.9. План сил для второй группы механизма в первом положении
Измеряем длину вектора , умножаем ее на масштаб, и результаты записываем в таблицу 3.

Таблица 3

Результаты определения реакций.

№ положения	R21, Н	, Н	, Н	R23, Н	R03, Н	R01, Н
0	55040	55040	12,25	18048	64	55040
1	10752	5408	-9270	5312	4928	10752
2	45792	45600	-4091	25888	9920	45792
3	40448	40448	12,25	19808	640	40448
4	44672	44480	4163,6	25120	9408	44672
5	10592	5088	9268,5	5312	4928	10592

Чтобы кривошип находился в равновесии, к нему необходимо приложить внешний уравновешивающий момент. Уравновешивающий момент определяется из соотношения, Н*м:

(15)

где h₂₁ – плечо уравновешивающей силы, которой является реакция R₁₂, м (см. рис 9).

Рассчитанные значения уравновешивающей силы F_УР и уравновешивающего момента Т_УР для всех пространственных положений механизма сводим в таблицу 4 и определяем максимальные значения уравновешивающей силы F_УРmax и уравновешивающего момента Т_УРmax

,

.