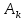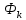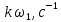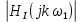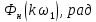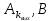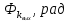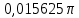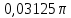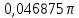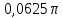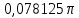Курсовая работа по тоэ(14 вар). Исследование линейной цепи в переходном и установившемся периодическом режимах
 Скачать 1.19 Mb. Скачать 1.19 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра ТОЭ Курсовая РАБОТА по дисциплине «Теоретические основы электротехники» Тема: Исследование линейной цепи в переходном и установившемся периодическом режимах Вариант 14
Санкт-Петербург 2018 ЗАДАНИЕ на курсовую работу Тема работы: исследование линейной цепи в переходном и установившемся периодических режимах 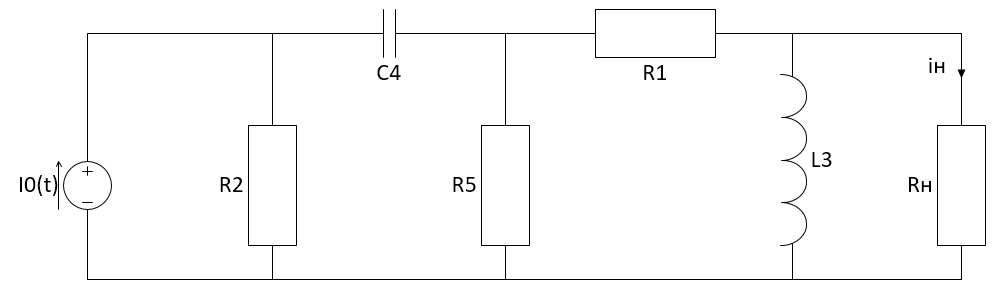 Рисунок 1. Исходная цепь 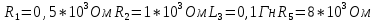 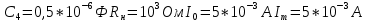 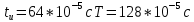 Содержание пояснительной записки: «Содержание», «Введение», Основные разделы, «Заключение», «Список использованных источников» СодержаниеВведение 4 1.Нормирование параметров электрической цепи 5 2.Расчёт операторной функции, временных и частотных характеристик цепи 6 2.1.Определение операторной функции передачи, её контроль по схемам замещения цепи, вычисление её полюсов 6 2.2.Нахождение операторным методом переходной и импульсной характеристики цепи, построение их графиков, контроль их соответствия цепи и друг другу 8 2.3.Нахождение АЧХ, ФЧХ и АФХ цепи, построение их графиков, контроль их соответствия цепи и друг другу 11 2.4.Определение полосы пропускания цепи графически 13 3.Анализ цепи операторным методом при апериодическом воздействии 14 3.1.Нахождение изображения воздействия, входного одиночного импульса, по Лапласу 14 3.2.Нахождение изображения искомой реакции по Лапласу 14 3.3.Нахождение оригинала реакции 14 3.5.Нахождение реакции цепи на изменённое по длительности воздействие 15 4.Качественный анализ цепи спектральным методом при апериодическом воздействии 15 4.1.Запись изображения по Фурье и нахождение непрерывных амплитудного и фазового спектра входного одиночного импульса исходной длительности. Построение графиков спектров, их контроль соответствия параметрам входного сигнала 15 4.2.Определение активной ширины амплитудного спектра графически 17 4.3.Качественное заключение об ожидаемых искажениях сигнала на выходе цепи 17 4.4.Оценка изменения активной ширины спектра исходного сигнала при изменении его длительности 17 4.5.Качественное заключение об ожидаемых искажениях сигнала на выходе 18 5.Анализ цепи спектральным методом при периодическом воздействии 18 5.1.Разложение в ряд Фурье заданного входного периодического сигнала. Построение графиков дискретных амплитудного и фазового спектров входного сигнала 18 5.2.Построение графиков входного сигнала, их контроль соответствия друг другу 20 5.3.Расчёт амплитудного и фазового спектров реакции, построение их графиков 21 5.4.Запись реакции цепи в виде отрезка ряда Фурье. Построение её графика в том же масштабе по оси абсцисс, что и в п. 5.2 23 Заключение 25 Список использованных источников 27 ВведениеЦель работы: практическое освоение современных методов количественного и качественного анализа линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники. Основные задачи: нахождение временных и частотных характеристик цепи анализ цепи операторным методом при апериодическом воздействии анализ цепи спектральным методом при периодическом и апериодическом воздействиях Используемые методы: метод пропорциональных величин, прямое и обратное преобразования Лапласа, операторные схемы замещения, уравнение связи переходной и импульсной характеристик цепи, формула корней квадратного уравнений, действия с комплексными числами, 10% критерий ширины спектра, критерий полосы пропускания (по половинной мощности), формулы коэффициентов ряда Фурье, уравнение связи длительности импульса и активной ширины амплитудного спектра. Нормирование параметров электрической цепи В качестве базисных значений возьмём: 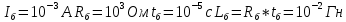 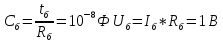 Нормированные значения величин обозначим индексом * (в дальнейшем индекс * будем опускать и писать, к примеру, вместо 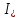 просто I, подразумевая нормированное значение величины, а не исходное): просто I, подразумевая нормированное значение величины, а не исходное):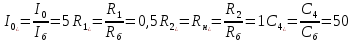 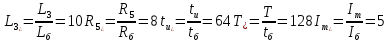 Так как в рассматриваемой цепи есть только одна катушка индуктивности и один конденсатор, то в дальнейшем, для простоты, будем писать L вместо 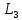 и C вместо и C вместо 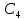 . .Расчёт операторной функции, временных и частотных характеристик цепи Определение операторной функции передачи, её контроль по схемам замещения цепи, вычисление её полюсов Для определения операторной функции передачи, построим операторную схему замещения исходной цепи, принимая независимые начальные условия нулевыми. 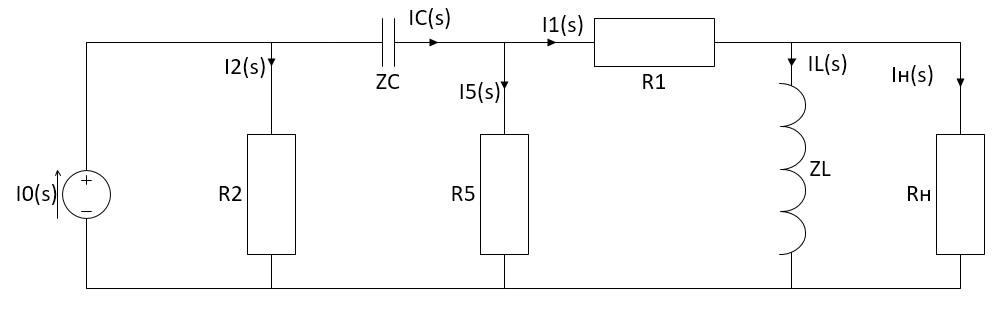 Рисунок 2. Операторная схема замещения исходной цепи 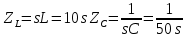 Найдём функцию передачи по методу пропорциональных величин: 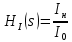 Пусть  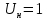 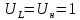 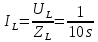 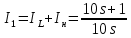 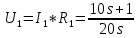 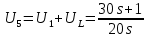 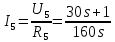 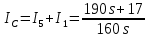 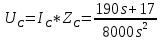 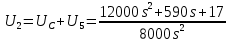 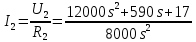 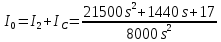 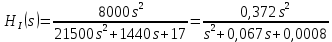 Проверим операторную функцию цепи по операторным схемам замещения в режимах 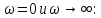 При 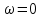 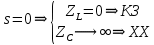 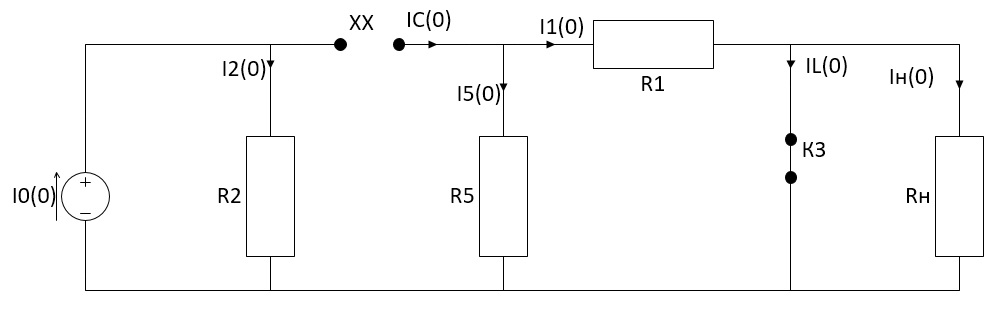 Рисунок 3. Операторная схема замещения при s=0 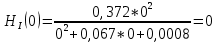 Из схемы на рисунке 3 видно, что 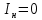 При 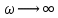 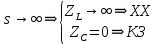 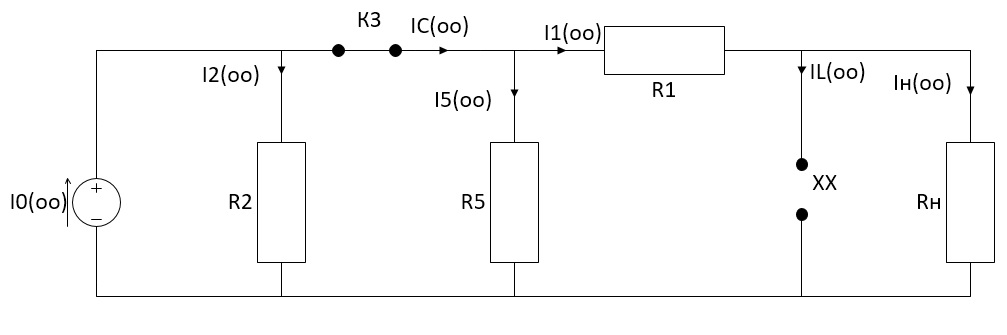 Рисунок 4. Операторная схема замещения при s 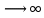 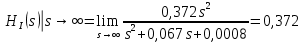 Из схемы на рисунке 4 видно, что 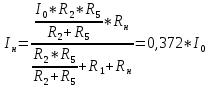 Таким образом, делаем вывод о том, что 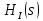 найдено верно. найдено верно.Найдём полюсы операторной функции передачи: 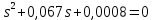 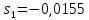 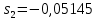 Построим найденные полюса на комплексной плоскости: 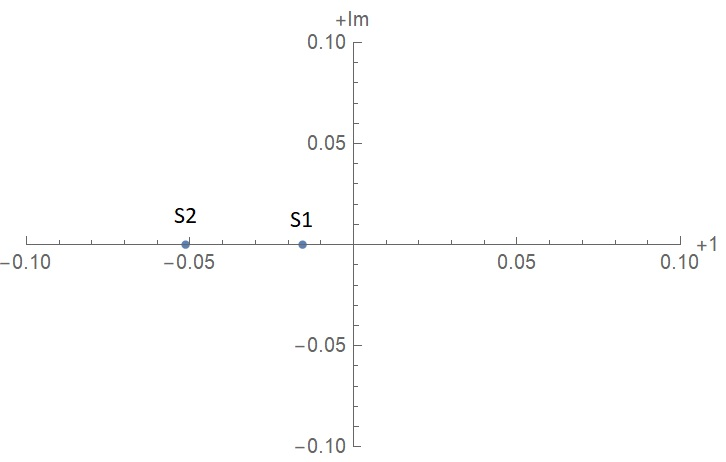 Рисунок 5. Полюсы операторной функции передачи Нахождение операторным методом переходной и импульсной характеристики цепи, построение их графиков, контроль их соответствия цепи и друг другу Преобразуем операторную функцию передачи по напряжению таким образом, чтобы можно было найти её оригинал, то есть импульсную характеристику цепи: 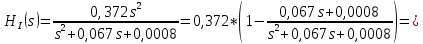 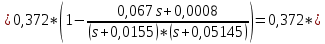 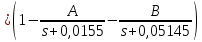 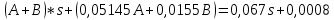 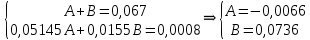 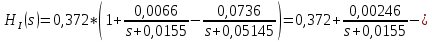 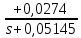 Найдём оригинал операторной функции передачи, используя теорему смещения. 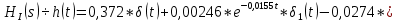 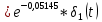 Изображение переходной характеристики равно 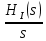 (по теореме об интегрировании оригинала), т.к. (по теореме об интегрировании оригинала), т.к. 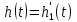 : :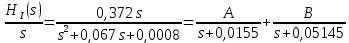 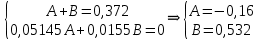 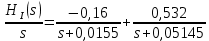 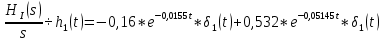 Сделаем проверку найденных переходной и импульсной характеристик цепи по уравнению связи между ними 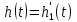 : :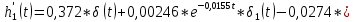 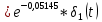 Значение производной переходной характеристики совпало со значением импульсной характеристики, найденным по операторной функции передачи цепи. Сделаем проверку найденной нами переходной характеристики по цепи в моменты времени 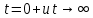 : :При 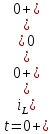 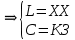 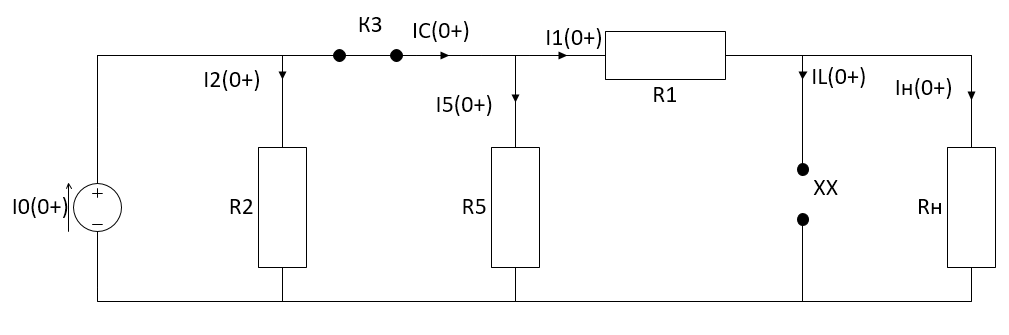 Рисунок 6. Схема цепи в момент времени t= 0+ 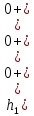 Из схемы рисунка 6 видно, что 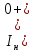 При 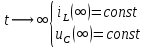 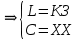 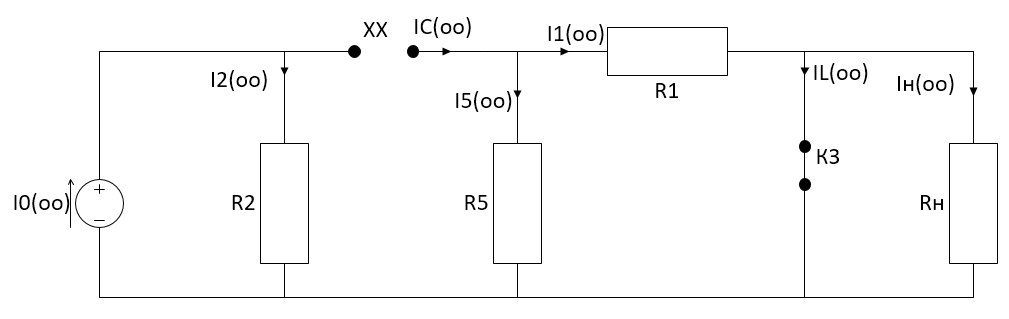 Рисунок 7. Схема цепи в момент времени 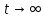 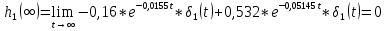 Из схемы рисунка 7 видно, что 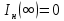 Таким образом, можно сделать вывод, что переходная, а значит и импульсная характеристика цепи найдены верно. Построим графики импульсной и переходной характеристик на одном графике: 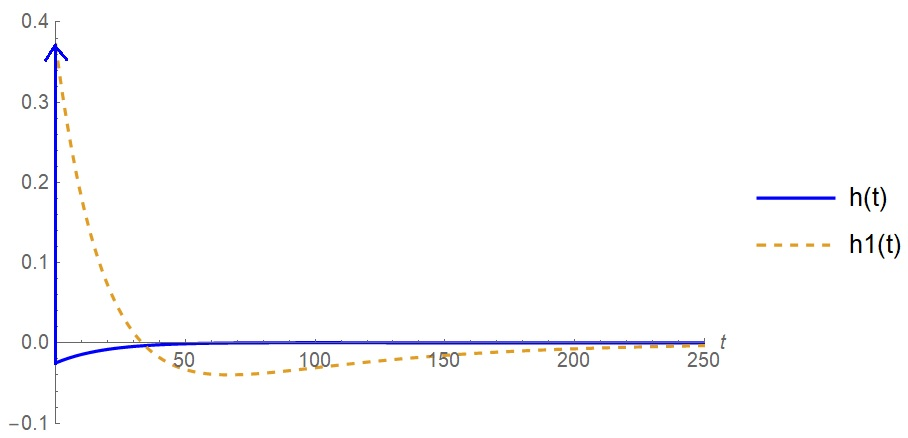 Рисунок 8. Графики переходной и импульсной характеристик цепи Нахождение АЧХ, ФЧХ и АФХ цепи, построение их графиков, контроль их соответствия цепи и друг другу Найдём амплитудно-фазовую характеристику цепи, сделав в операторной функции передачи цепи замену 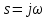 : :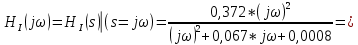 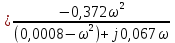 Найдём амплитудно-частотную характеристику цепи по АФХ: 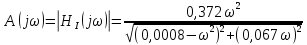 Найдём фазочастотную характеристику цепи по АФХ: 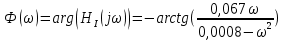 Сделаем проверку найденной АЧХ по значениям операторной функции передачи при 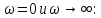 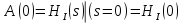 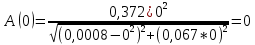 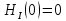 (см. пункт 2.1) (см. пункт 2.1)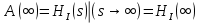 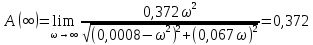 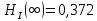 (см. пункт 2.1) (см. пункт 2.1)АЧХ соответствует цепи, т.к. 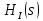 соответствует цепи и выше мы делали проверку АЧХ по соответствует цепи и выше мы делали проверку АЧХ по 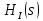 . .Построим графики АФХ, АЧХ и ФЧХ: 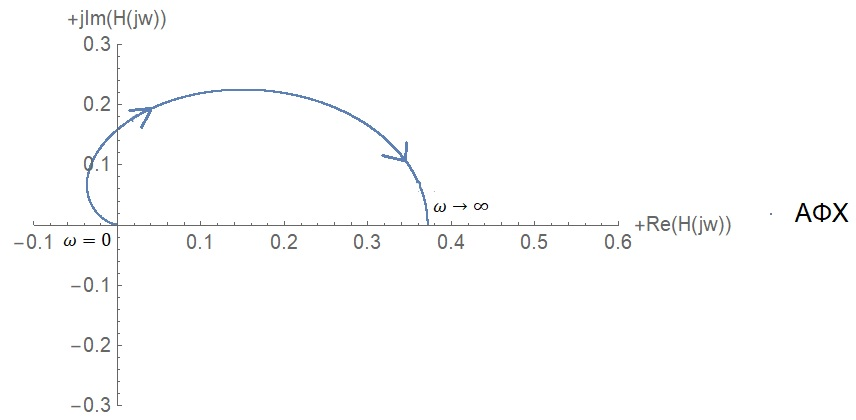 Рисунок 9. График АФХ цепи 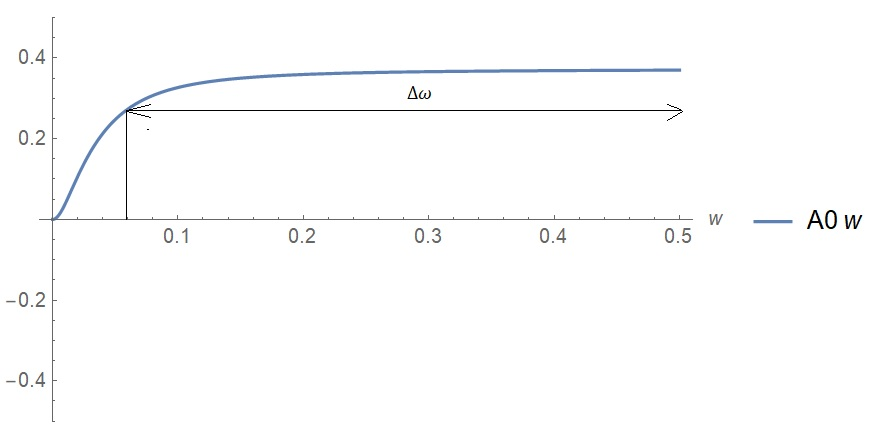 Рисунок 10. График АЧХ цепи 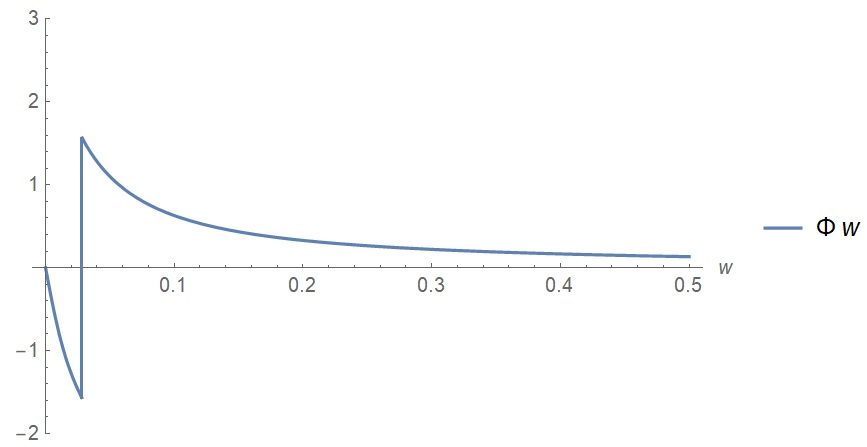 Рисунок 11. График ФЧХ цепи Проверим соответствие АЧХ и ФЧХ АФХ цепи по их графикам: 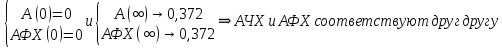 ФЧХ цепи вначале убывает из отрицательного значения, затем изменяется скачком на положительное значение и убывает до нуля на бесконечности. Действительная часть АФХ вначале отрицательна, затем она переходит через ноль, становясь положительной. Мнимая часть АФХ всегда положительная и убывает до нуля на бесконечности. Таким образом, ФЧХ и АФХ цепи соответствуют друг другу. Определение полосы пропускания цепи графически Определим полосу пропускания цепи по рисунку 10 по уровню 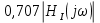 : :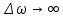 Анализ цепи операторным методом при апериодическом воздействии Нахождение изображения воздействия, входного одиночного импульса, по Лапласу Запишем воздействие типа меандр в виде разности двух ступенчатых воздействий с запаздыванием, равным 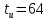 : :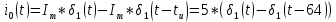 Найдём изображение входного одиночного импульса, используя теорему запаздывания и изображение единичной ступенчатой функции: 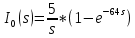 Нахождение изображения искомой реакции по Лапласу Изображение искомой реакции связано с изображением входного воздействия следующим соотношением: 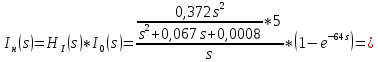 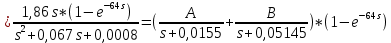 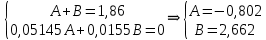 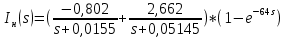 Нахождение оригинала реакции Найдём оригинал реакции используя теоремы смещения и запаздывания: 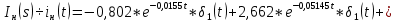 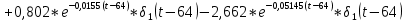 Построение графиков воздействия и реакции 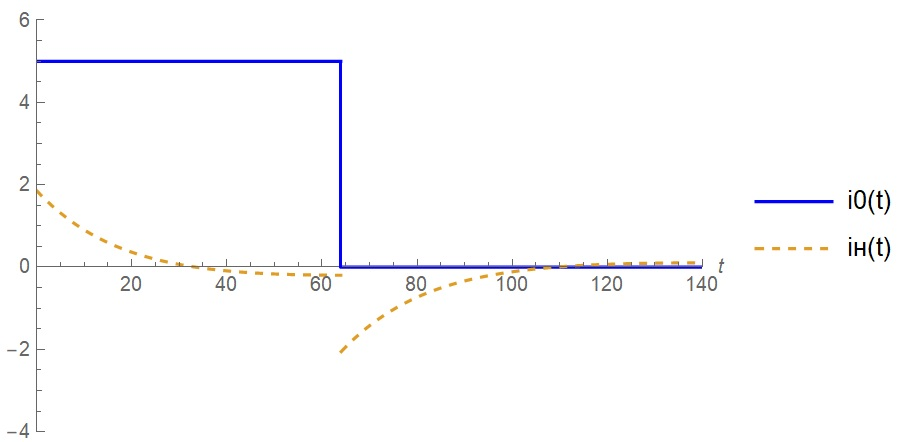 Рисунок 12.Графики входного воздействия и реакции Нахождение реакции цепи на изменённое по длительности воздействие В нашем случае цепь является ФВЧ-цепью (на основании положения полосы пропускания на рисунке 10). Уменьшим длительность импульса в три раза и примем 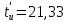 . Запишем реакцию цепи на воздействие втрое меньшей длительности: . Запишем реакцию цепи на воздействие втрое меньшей длительности: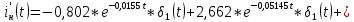 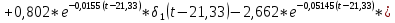 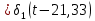 Качественный анализ цепи спектральным методом при апериодическом воздействии Запись изображения по Фурье и нахождение непрерывных амплитудного и фазового спектра входного одиночного импульса исходной длительности. Построение графиков спектров, их контроль соответствия параметрам входного сигнала Запишем изображение входного импульса по Фурье, сделав в изображении этого импульса по Лапласу замену 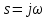 : :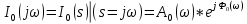 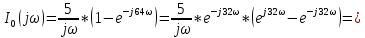 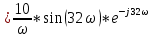 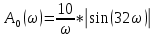 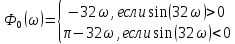 Сделаем проверку найденных нами спектров, найдя значение амплитудного спектра на нулевой частоте: 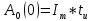 Вычислим значение амплитудного спектра при нулевой частоте, воспользовавшись тем, что при малых углах 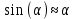 : :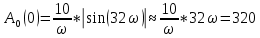 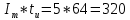 На основании проделанных вычислений делаем вывод о том, что амплитудный спектр найден верно. 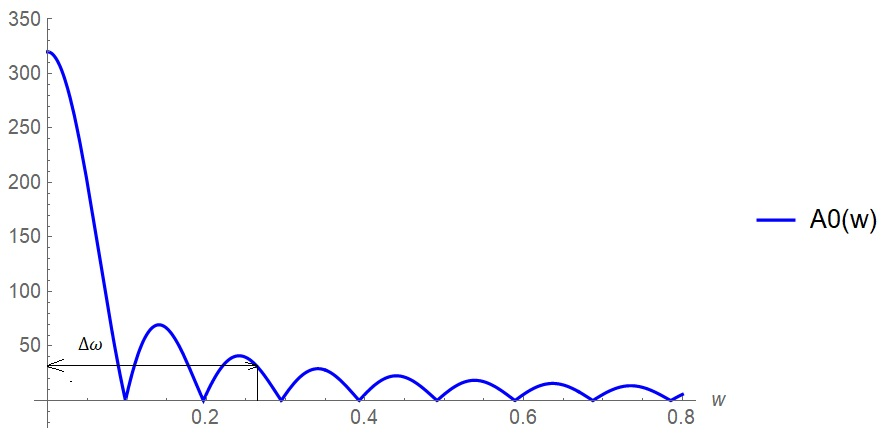 Рисунок 13. График непрерывного амплитудного спектра входного одиночного импульса 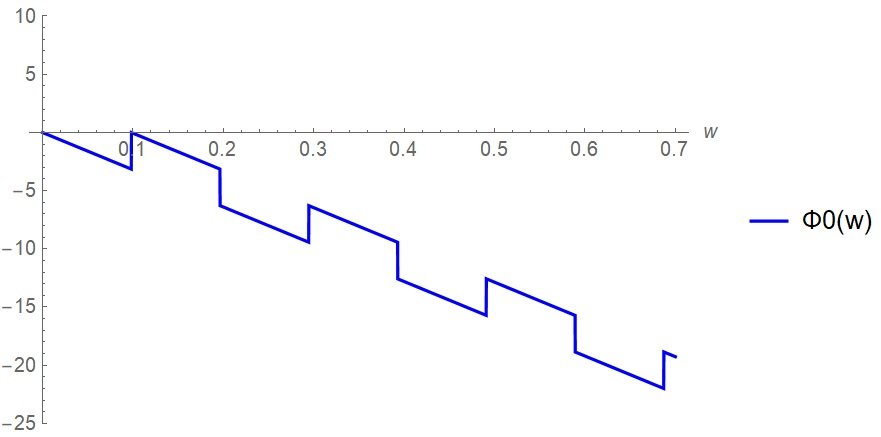 Рисунок 14. График непрерывного фазового спектра входного одиночного импульса Определение активной ширины амплитудного спектра графически Определим по рисунку 13 активную ширину спектра, используя 10%-критерий: 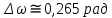 Качественное заключение об ожидаемых искажениях сигнала на выходе цепи В результате сравнения АЧХ цепи (рисунок 10) и амплитудного спектра входного одиночного импульса (рисунок 13), можно сделать следующие предположения об искажениях сигнала на выходе цепи: Низкочастотные гармоники очень сильно затухают и практически не проходят через цепь. Существенная часть входного сигнала лежит вне полосы пропускания, что позволяет предположить, что сигнал на выходе будет очень сильно искажён: у выходного сигнала будет отсутствовать плато (в силу отсутствия низкочастотных гармоник), а, значит, будет наблюдаться пик. Оценка изменения активной ширины спектра исходного сигнала при изменении его длительности Длительность импульса исходного сигнала и активная ширина его спектра связаны между собой следующим соотношением: 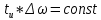 В пункте 3.5. мы уменьшили длительность исходного импульса в три раза. Тогда активная ширина спектра исходного сигнала увеличится в три раза. Качественное заключение об ожидаемых искажениях сигнала на выходе При уменьшении длительности входного импульса активная ширина амплитудного спектра входного сигнала увеличилась в три раза, а это означает, что большая, чем при исходной длительности, часть амплитудного спектра входного сигнала лежит в полосе пропускания. Поэтому можно сделать предположение о том, что будут наблюдаться меньшие искажения. Анализ цепи спектральным методом при периодическом воздействии Разложение в ряд Фурье заданного входного периодического сигнала. Построение графиков дискретных амплитудного и фазового спектров входного сигнала Найдём частоту первой гармоники: 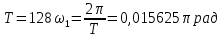 Найдём коэффициенты ряда Фурье для заданного входного периодического сигнала: 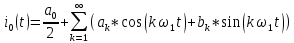 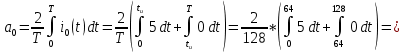 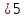 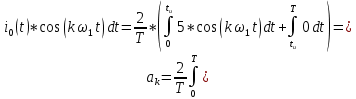 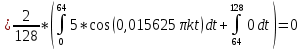 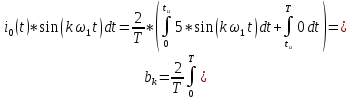 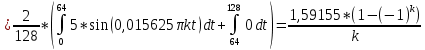 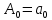 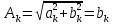 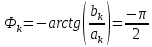 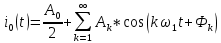 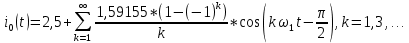 Построим графики дискретных амплитудного и фазового спектров входного сигнала: 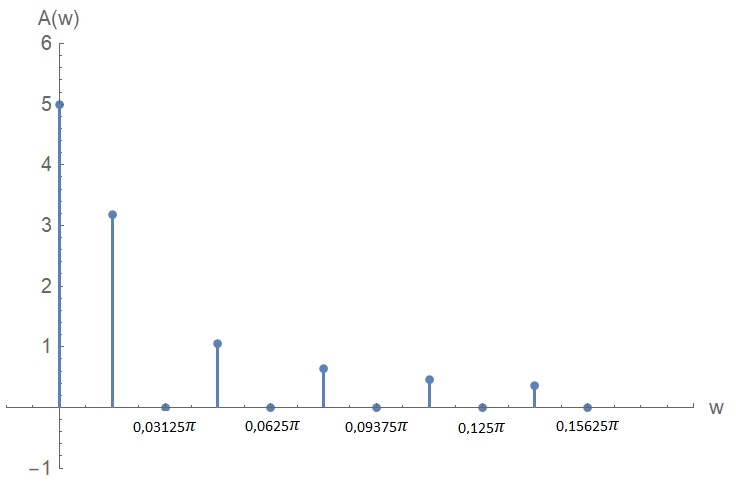 Рисунок 15. График дискретного амплитудного спектра входного сигнала 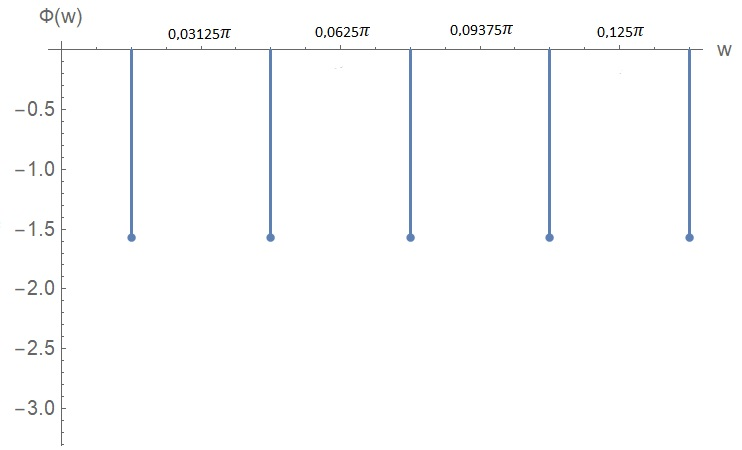 Рисунок 16.График дискретного фазового спектра входного сигнала Построение графиков входного сигнала, их контроль соответствия друг другу Построим на одном графике входной периодический сигнал и его аппроксимацию отрезком ряда Фурье. Число гармоник отрезка ряда определим по 10%-му критерию. Для этого построим таблицу значений 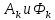 : :
Таблица 1. Значения коэффициентов ряда Фурье входного периодического сигнала Таким образом, в соответствии с таблицей 1, учитываем только первые пять гармоник (амплитуды двух из них равны 0); аппроксимирующий отрезок ряда Фурье имеет следующий вид: 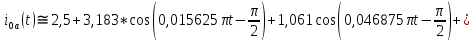 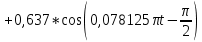 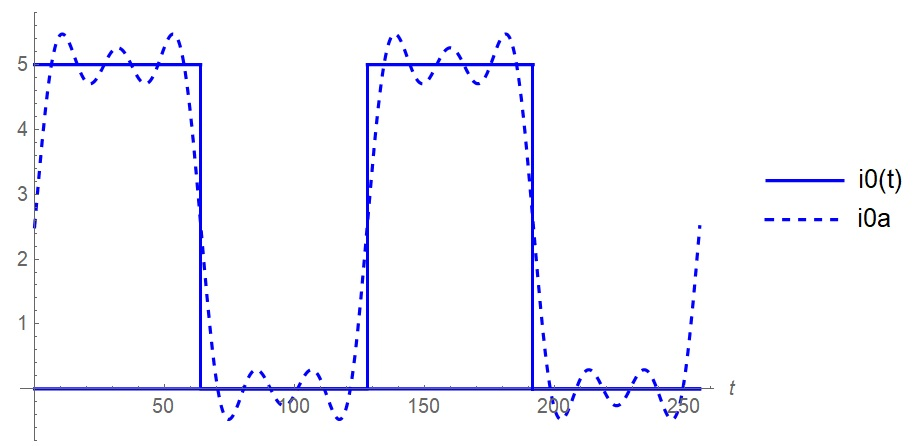 Рисунок 17. Графики входного сигнала и его аппроксимация отрезком ряда Фурье Из рисунка 17 мы видим, что аппроксимирующий отрезок ряда Фурье и исходный входной периодический сигнал практически идентичны по форме. Расчёт амплитудного и фазового спектров реакции, построение их графиков Амплитуды и начальные фазы гармоник выходного напряжения связаны с амплитудами и гармониками входного напряжения следующими формулами: 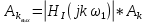 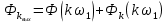 Рассчитаем амплитудный и фазовый спектры реакции, сведя результаты вычислений в таблицу:
Таблица 2. Значения коэффициентов ряда Фурье выходного сигнала Построим дискретные амплитудный и фазовый спектры выходного сигнала: 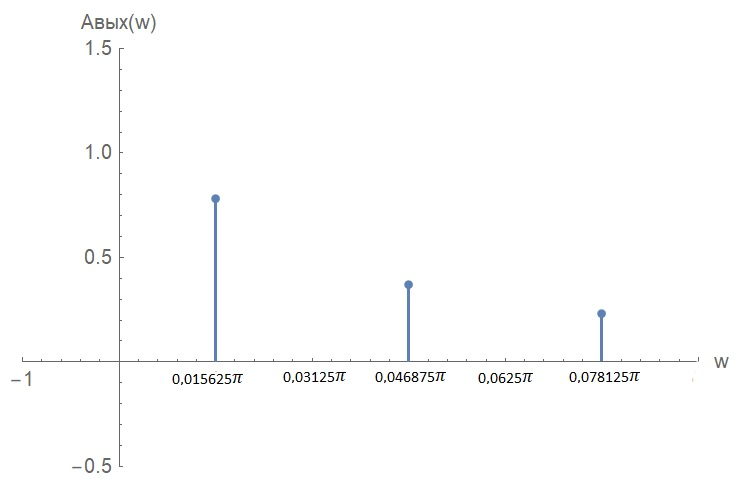 Рисунок 18. График дискретного амплитудного спектра выходного сигнала 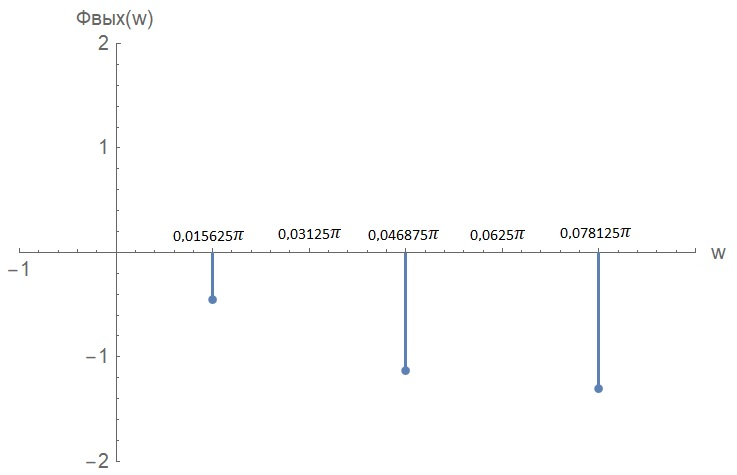 Рисунок 19. График дискретного фазового спектра выходного сигнала Запись реакции цепи в виде отрезка ряда Фурье. Построение её графика в том же масштабе по оси абсцисс, что и в п. 5.2 Запишем реакцию цепи в виде отрезка ряда Фурье, ограничившись пятой гармоникой: 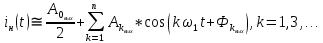 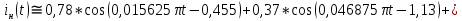 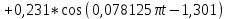 Построим график выходного сигнала, на основании разложения его в ряд Фурье: 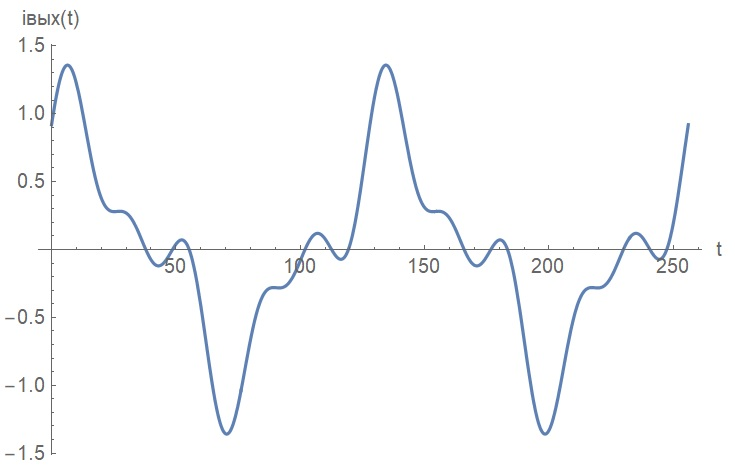 Рисунок 20. График выходного сигнала в приближении первыми пятью гармониками ряда Фурье ЗаключениеНа основании данной курсовой работы можно сделать следующие выводы Расчёт операторной функция передачи цепи, представленной на рисунке 2, показал, что: 1.1 Функция передачи имеет два различных действительных полюса (см. рисунок 5), следовательно, переходная и импульсная характеристики имеют апериодический характер (см. графики на рисунке 8) 1.2 Цепь представляет из себя фильтр высоких частот (график АЧХ цепи на рисунке 10) Полоса пропускания цепи, определённая по рисунку 10, составляет: 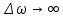 По цепи, представленной на рисунке 2, операторным методом можно сделать следующие выводы: 2.1 Реакция имеет апериодический характер (рисунок 12) 2.2 На графике реакции отсутствует подъём (выходит не из нуля, а из определённого значения), длительность спада больше по сравнению со входным сигналом: убывание происходит в период времени от 0 до 64, затем реакция меняет полярность и тот же самый процесс наблюдается в обратную сторону Спектральный анализ входного апериодического сигнала показал, что: Активная ширина амплитудного спектра равна: 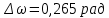 ( рисунок 13) ( рисунок 13)Предположения об искажениях входного сигнала, сделанные на основе АЧХ цепи, при его прохождении через цепь приведены в пункте 4.3 При уменьшении длительности входного импульса в три раза, активная ширина амплитудного спектра входного сигнала увеличивается в три раза Предположения об искажениях входного сигнала уменьшенной длительности, сделанные на основе АЧХ цепи, при его прохождении через цепь приведены в пункте 4.5 4.Спектральный анализ входного периодического сигнала показал, что: Входной периодический сигнал представляется в виде последовательных прямоугольных импульсов Ряд Фурье входного сигнала имеет постоянную составляющую, равную половинной амплитуде входного сигнала, состоит из cos и не имеет чётных гармоник (их амплитуды равны нулю), а фазы гармоник равны 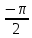 Ряд Фурье выходного сигнала не имеет постоянной составляющей, т.к. передаточная функция равна 0 на нулевой частоте, состоит из cos, не имеет чётных гармоник (их амплитуды равны 0), а фазы стремятся к 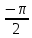 Список использованных источниковКурсовое проектирование по теоретической электротехнике: Учеб. пособие / Под ред. Ю. А. Бычкова, Е.Б. Соловьевой, Э. П. Чернышева. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2013. 128 с. Основы теоретической электротехники: Учебное пособие. 2-е издание., стер. – СПб.: Изд-во «Лань», 2009. – 592 с. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||