ДНГ. Исследование полученной модели 49
 Скачать 7.73 Mb. Скачать 7.73 Mb.
|
3.9. Расчёт жёсткости газодинамической опорыРассчитаем жёсткость газодинамической опоры, исходя из её экспериментально измеренной несущей способности. На рис. 3.9 представлена вращающаяся часть ДНГ. Она представляет собой вал с закреплённым на нём маховиком, ротором двигателя и двумя полусферами ГДО с распорной втулкой. 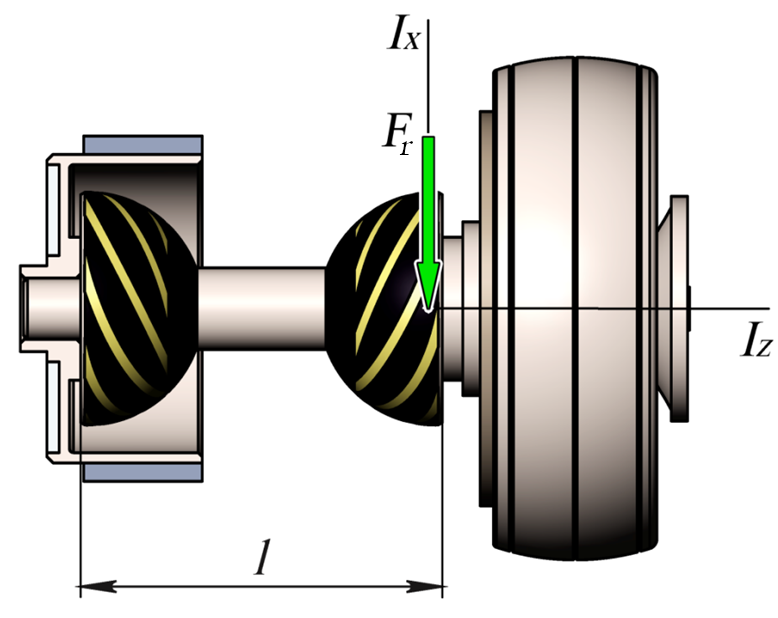 Рис. 3.9. Вращающаяся часть ДНГ Анализ трёхмерной модели показал, что центр масс вращающейся части почти точно совпадает с полюсом правой полусферы (ближайшей к маховику), это говорит о том, что правая полусфера воспринимает практически всю радиальную нагрузку. Это обстоятельство позволяет проводить расчёт радиальной жёсткости опоры, исходя из перемещения правой полусферы под действием перегрузки, в предположении, что в ней сосредоточен вес всей вращающейся части. Тогда радиальную жёсткость опоры можно найти по формуле:
где m – масса вращающейся части; nr – несущая способность опоры в радиальном направлении; g – ускорение свободного падения, g ≈ 9,8 м/с2; Δ – эффективный зазор между рабочими поверхностями ГДО. Осевая жёсткость рассчитывается по формуле:
где na – несущая способность опоры в осевом направлении. Угловую жёсткость ГДО найдём по формуле:
где l – расстояние между полюсами полусфер. Параметры газодинамической опоры ДНГ КИНД05-091 [1] и результаты расчёта её жёсткости представлены в таблице 3.6. Таблица 3.6. Параметры ГДО
Таким образом, мы получили значение угловой жёсткости скоростной опоры: К2 =Kγ = 600 (Н∙м/рад) Поскольку несущая способность, ровно как и величина эффективного зазора между рабочими поверхностями ГДО, различаются у разных образцов ДНГ, расчёт носит приближённый характер. 3.10. Исследование полученной моделиИсследуем влияние угловой жёсткости скоростной опоры на функционирование ДУС на ДНГ КИНД05-091 в среде Matlab Simulink. Для этого построим в Simulink полученную математическую модель и добавим к ней два канала обратной связи (приложение Б). Теперь, используя модель, построенную в Simulink, проведём виртуальный эксперимент: предположим, что измерительная ось Х прибора направлена вертикально вверх, а ось Y – на север (рис. 3.10). 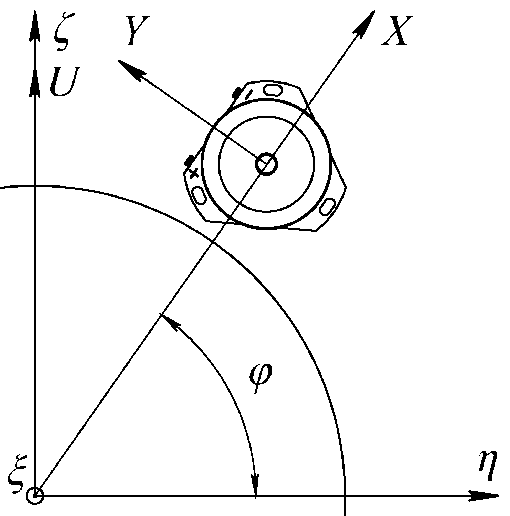 Рис. 3.10. Ориентация прибора относительно осей географического трёхгранника ξηζ Тогда канал Х прибора измеряет вертикальную составляющую угловой скорости суточного вращения Земли, а канал Y – горизонтальную:
где U – угловая скорость суточного вращения Земли, U ≈ 7,27·10-5 рад/с; φ – географическая широта местности, φ ≈ 56° для Москвы. При этом в обмотках датчиков момента должны протекать токи:
Результаты моделирования представлены на графиках ниже. 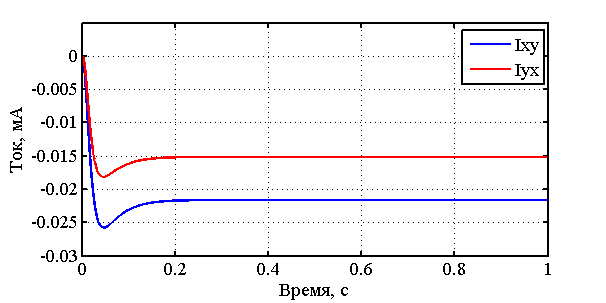 Рис. 3.11. Изменение токов ОС 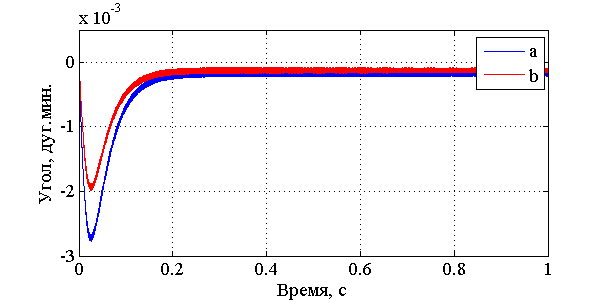 Рис. 3.12. Изменение углов наклона маховика относительно корпуса 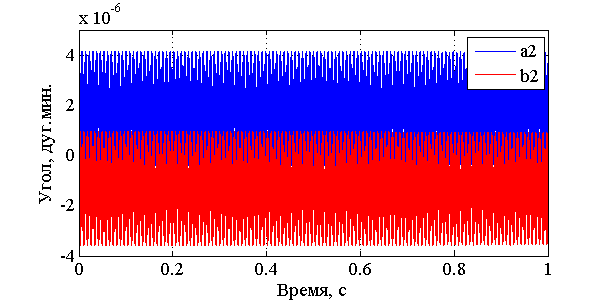 Рис. 3.13. Изменение углов наклона вала относительно корпуса Из графика, представленного на рис. 3.11, видно, что токи в обмотках датчиков момента в установившемся режиме принимают расчётные значения (34). Это говорит об адекватности построенной модели. При этом маховик остаётся отклонённым относительно корпуса (рис. 3.12) на некоторую малую величину статической ошибки (порядка 10-4 дуг. мин.). Из графика рис. 3.13 видно, что вал отклонён относительно корпуса (наклон порядка 2·10-6 дуг. мин.) и при этом совершает колебания. Если ближе посмотреть на график углов наклона маховика относительно вала, можно увидеть его нутационные колебания (рис. 3.14). 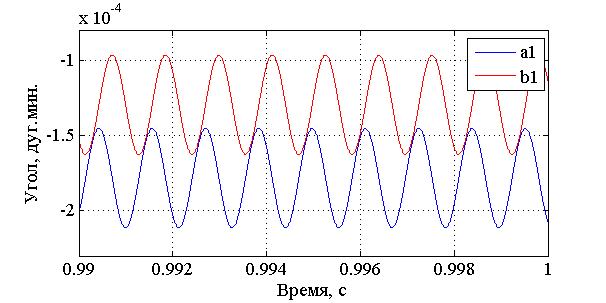 Рис. 3.14. Нутационные колебания маховика Параметры нутационных колебаний маховика:
Частоту нутационных колебаний маховика можно рассчитать по формуле:
Видим, что расчётное значение нутационной частоты совпадает с полученным при моделировании. Если ближе посмотрим на график колебаний вала относительно корпуса, то увидим, что помимо колебаний на собственной частоте опоры присутствуют также биения на нутационной частоте привода (рис. 3.15). 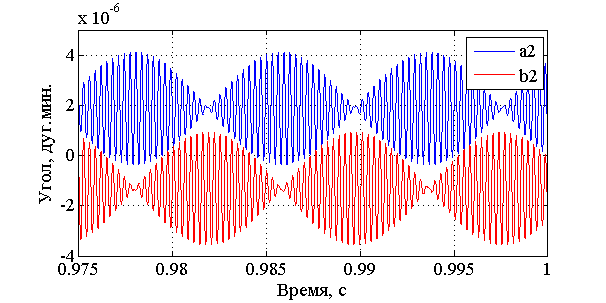 Рис. 3.15. Колебания и биения вала относительно корпуса Параметры колебаний и биений вала:
Нутационную частоту привода можно оценить по формуле:
Частота собственных колебаний в опоре рассчитывается:
Расчётные значения частот 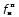 и и 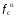 почти точно совпадают с полученными при моделировании. почти точно совпадают с полученными при моделировании.Сравнивая графики рис. 3.14 и рис. 3.15, стоит отметить, что диапазон изменения углов наклона маховика относительно вала на два порядка превышает диапазон изменения углов наклона вала относительно корпуса при заданной жёсткости скоростной опоры. В конечном итоге, колебания вала относительно корпуса складываются из нутационных колебаний маховика относительно вала и колебаний вала относительно корпуса и выглядят, как представлено на графике рис. 3.16. 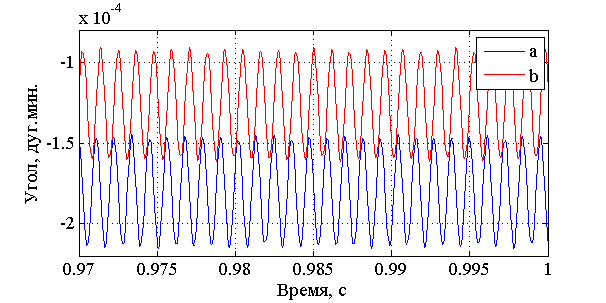 Рис. 3.16. Колебания вала относительно корпуса. Датчики угла фиксируют углы наклона вала относительно корпуса и выдают соответствующие сигналы в каналы обратной связи. Сигналы, снимаемые из обмоток датчиков момента, (рис. 3.11) при ближайшем рассмотрении выглядят, как представлено на графике рис. 3.17 (на примере Iyx). 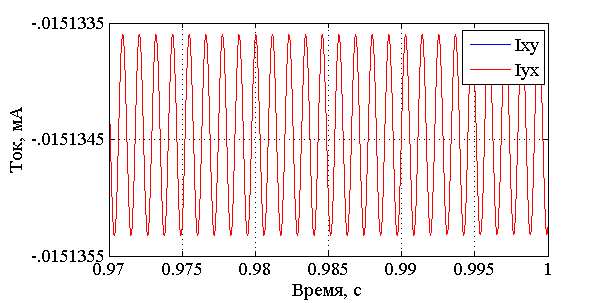 Рис. 3.17. Колебания выходного сигнала Из графика рис. 3.17 видно, что в выходном сигнале присутствуют колебания на нутационной частоте маховика. Параметры этих колебаний:
Коэффициент передачи нутационных колебаний через канал обратной связи равен:
При действии на корпус прибора вибрации она через опору передаётся на маховик. Оценим действие вибрации на функционирование ДНГ. Представим, что на вал вокруг оси X действует переменный возмущающий момент, вызванный наличием внешней вибрации. Этот момент вызывает колебания маховика относительно корпуса на частоте возмущения. На амплитудно-частотной характеристике (АЧХ), представленной на рис. 3.18, по оси абсцисс в логарифмическом масштабе отложена частота возмущающего момента, приложенного к валу по оси Х, а по оси ординат – отношение угла наклона маховика относительно корпуса вокруг соответствующей оси к амплитуде возмущающего момента, выраженное в децибелах. Таким образом, графики рис. 3.18 характеризуют реакцию прибора на возмущение, действующее по оси X: верхний – реакцию по углу α (наклон вокруг X), а нижний – реакцию по углу β (наклон вокруг Y). То есть верхний график характеризует реакцию по оси действия возмущения, нижний – по перпендикулярной ей оси. 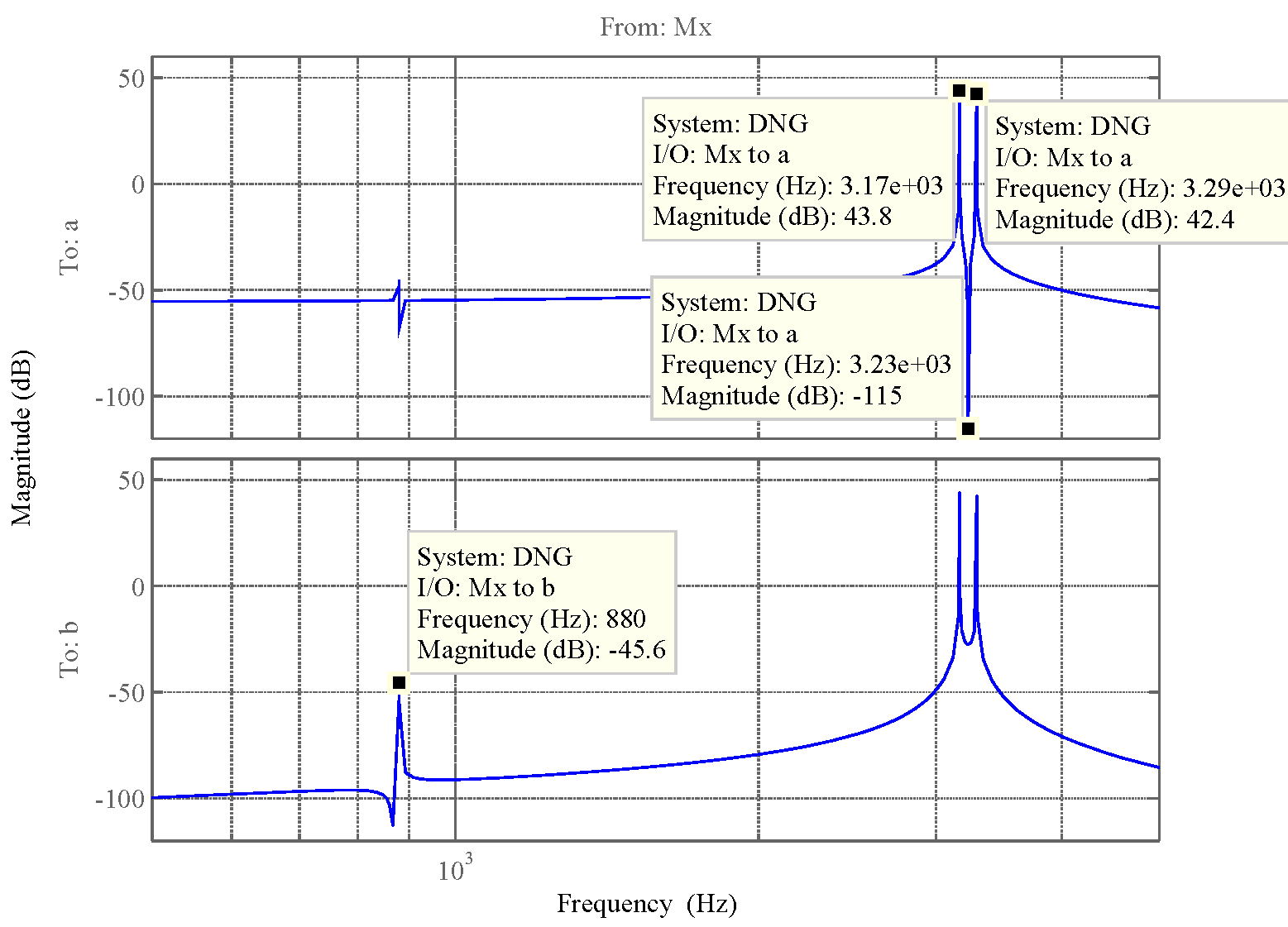 Рис. 3.18. АЧХ прибора, характеризующая зависимость углов наклона маховика относительно корпуса от момента, приложенного к валу (при К2 =600 Н∙м/рад) Анализируя АЧХ рис. 3.18, можно выделить следующие характерные частоты: – 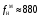 (Гц) – частота нутационных колебаний маховика, на ней возникает резонанс по оси, перпендикулярной к оси действия возмущения; (Гц) – частота нутационных колебаний маховика, на ней возникает резонанс по оси, перпендикулярной к оси действия возмущения;– 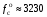 (Гц) – собственная частота опоры, на ней наблюдается антирезонанс; (Гц) – собственная частота опоры, на ней наблюдается антирезонанс;– 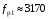 (Гц), (Гц), 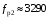 (Гц) – резонансные частоты, близкие к собственной частоте опоры. (Гц) – резонансные частоты, близкие к собственной частоте опоры.Интересным является тот факт, что собственная частота опоры 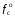 не является резонансной, а даже наоборот – колебания на этой частоте, подавляются. При этом резонанс проявляется на частотах не является резонансной, а даже наоборот – колебания на этой частоте, подавляются. При этом резонанс проявляется на частотах 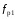 , , 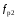 , лежащих вблизи неё. , лежащих вблизи неё.Как отмечалось ранее, при работе ДНГ возникают вибрации на частотах кратных частоте вращения ротора. Наиболее ярко проявляются колебания на двойной частоте собственного вращения 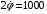 Гц [1]. Гц [1].Резонанс со второй гармоникой возможен при двух значениях угловой жёсткости скоростной опоры:
Для предотвращения возникновения резонанса на двойной частоте вращения ротора при проектировании ДНГ нужно избегать подобных значений жёсткости скоростной опоры. 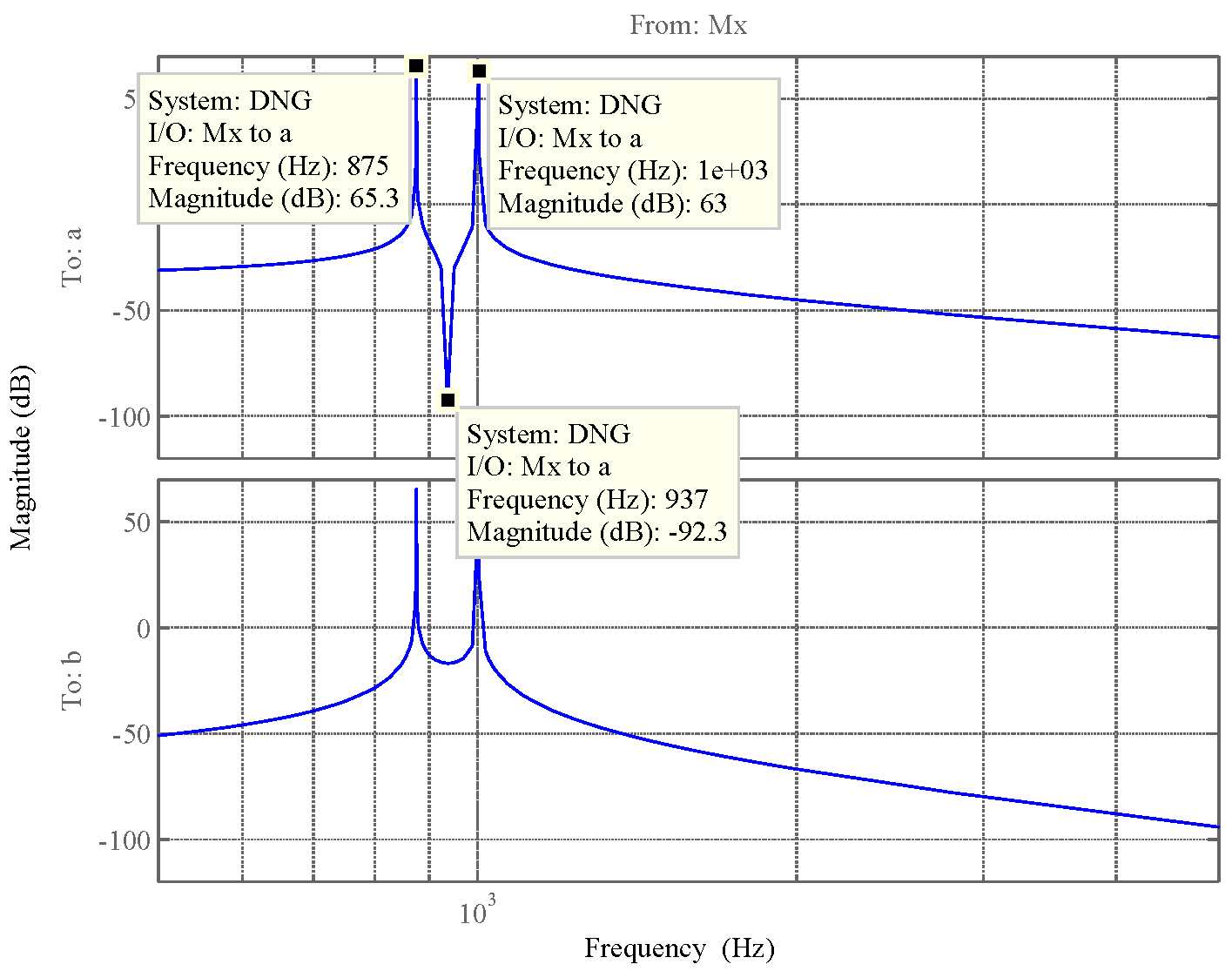 Рис. 3.19. АЧХ прибора, характеризующая зависимость углов наклона маховика относительно корпуса от момента, приложенного к валу (при К2 =50,5 Н∙м/рад) Сравнивая АЧХ рис. 3.18 и 3.19, можно заметить, что снижение угловой жёсткости опоры ведёт к поднятию АЧХ, а следовательно, к снижению виброустойчивости ДНГ. Поэтому при проектировании стоит стремиться получить как можно большее значение жёсткости скоростной опоры, тем более, что это ведёт к увеличению её несущей способности. |

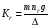
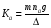
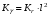
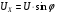
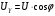
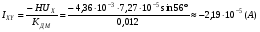
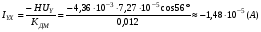
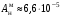 (дуг. мин.)
(дуг. мин.)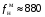 (Гц)
(Гц)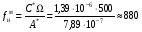 (Гц)
(Гц)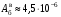 (дуг. мин.) – размах биений
(дуг. мин.) – размах биений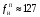 (Гц) – частота биений (нутационная)
(Гц) – частота биений (нутационная)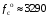 (Гц) – частота колебаний (собственная)
(Гц) – частота колебаний (собственная)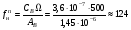 (Гц)
(Гц)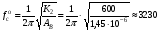 (Гц)
(Гц)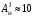 (нА)
(нА)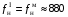 (Гц)
(Гц)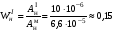 (мА/дуг. мин.)
(мА/дуг. мин.)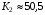 (Н∙м/рад),
(Н∙м/рад), 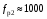 (Гц) (рис.3.19)
(Гц) (рис.3.19)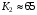 (Н∙м/рад),
(Н∙м/рад), 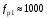 (Гц)
(Гц)