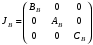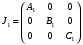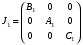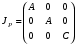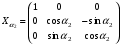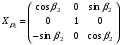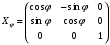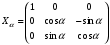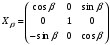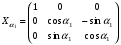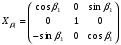ДНГ. Исследование полученной модели 49

• Название: Исследование полученной модели 49
• Анкор: ДНГ.docx
• Дата: 22.04.2017
• Размер: 7.73 Mb.
• Имя файла: ДНГ.docx
• Тип: Исследование; #4996
• страница: 6 из 15

3.6. Механическая модель динамически настраиваемого гироскопа

Рассмотрим динамически настраиваемый гироскоп как механическую систему, состоящую из вала, двух колец внутреннего кардана и ротора [2]. Она представлена на рис. 3.3.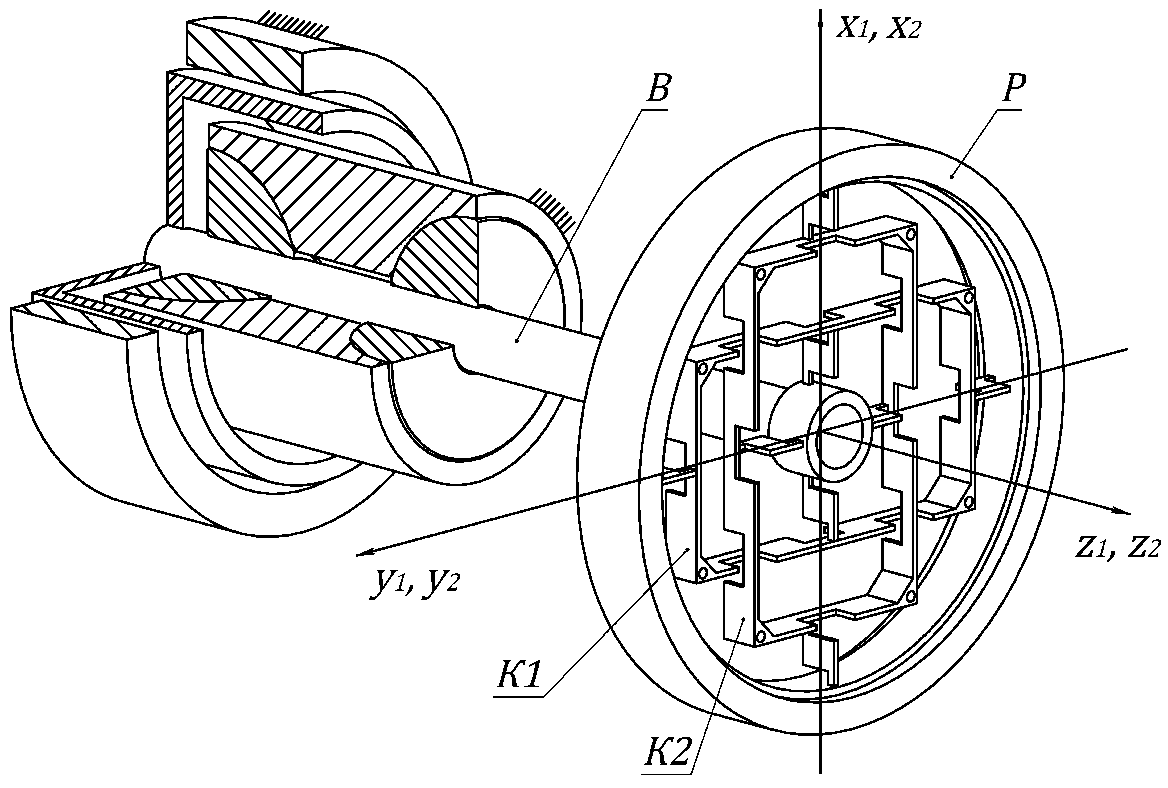



Рис. 3.3. Механическая модель ДНГ

Вал имеет три угловые степени свободы относительно основания и связан с кардановыми кольцами через упругие элементы, каждый из которых имеет угловую податливость вокруг одной оси. Таким образом, первое кольцо может отклоняться относительно вала вокруг оси y₁, а второе – вокруг оси x₂.

Маховик также связан с кардановыми кольцами через упругие элементы и отклоняется относительно первого кольца вокруг осиx₁, относительно второго – вокруг оси y₂.

В невозмущённом состоянии системы оси систем координат x₁y₁z₁ и x₂y₂z₂ совпадают.

Введём следующие системы координат:

XYZ – система координат, связанная с основанием (корпусом);

x_вy_вz_в – система координат, связанная с валом, не участвующая в собственном вращении;

xyz – система координат, связанная с маховиком, не участвующая в собственном вращении;

x₁y₁z₁ – система координат, связанная с первым кольцом;

x₂y₂z₂ – система координат, связанная со вторым кольцом;

x’y’z’ – система координат, связанная с ротором.

Основание движется относительно инерциального пространства с угловой скоростью, которая проецируется на оси, связанные с основанием как (ω_X, ω_Y, ω_Z).

Положение вала относительно основания задаётся последовательностью двух поворотов: на угол α₂ вокруг оси X и на угол β₂ вокруг оси y_в(рис. 3.4).



Рис. 3.4. Положение вала относительно основания

Положение ротора относительно вала задаётся последовательностью двух поворотов: на угол α₁ вокруг оси x_ви на угол β₁ вокруг оси y (рис. 3.5).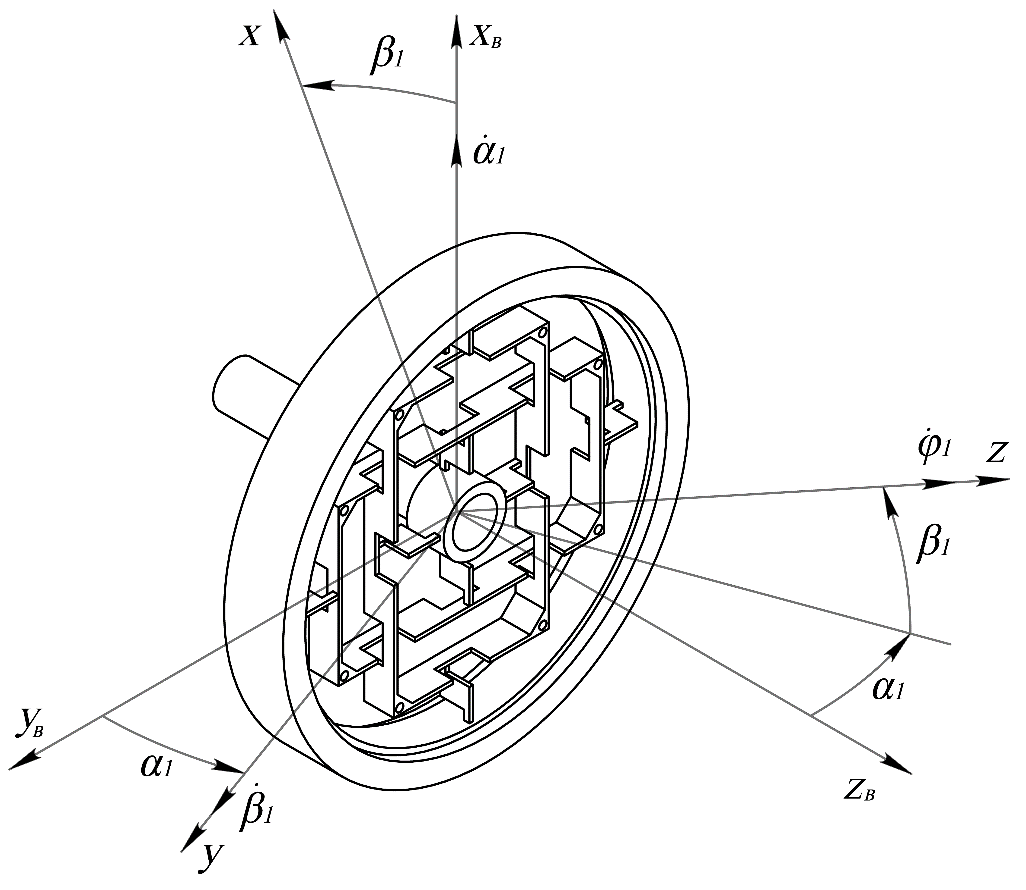



Рис. 3.5. Положение ротора относительно вала

Положение первого кольца относительно вала задаётся последовательностью поворотов: на угол φ вокруг оси Z_в и на угол α вокруг оси x₁ (рис. 3.6).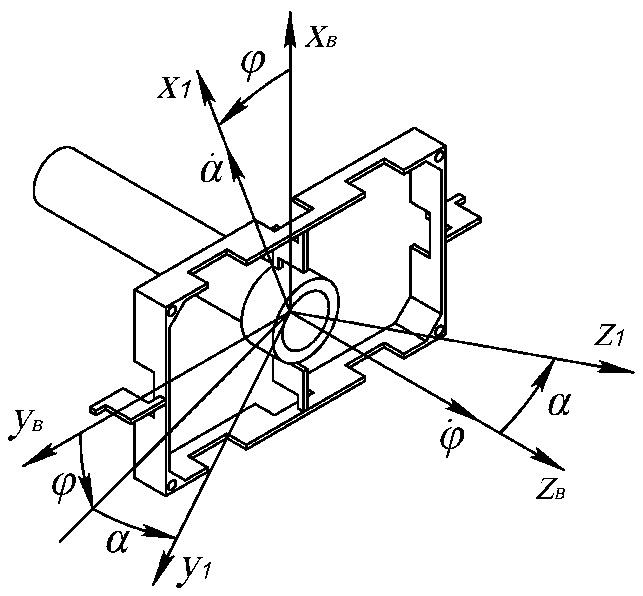



Рис. 3.6. Положение первого кольца относительно вала

Положение второго кольца относительно вала задаётся поворотом системы координат на угол φ вокруг оси Z_в и поворотом на угол β вокруг
оси y₂ (рис. 3.7).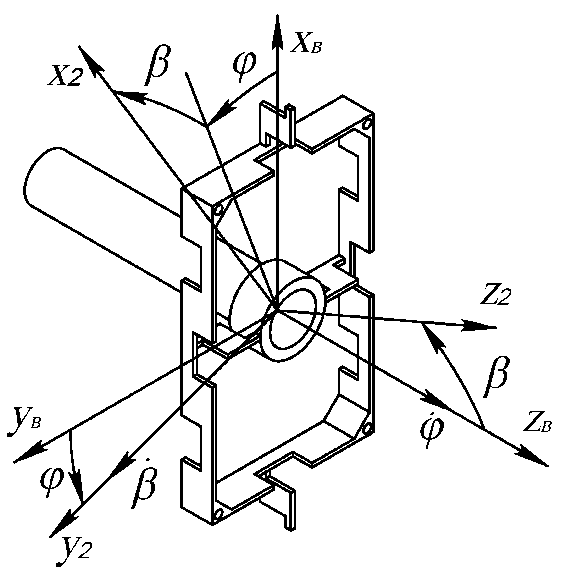



Рис. 3.7. Положение второго кольца относительно вала

Положение ротора относительно первого кольца задаётся поворотом системы координат, связанной с первым кольцом, на угол β вокруг оси y₁ (рис. 3.8).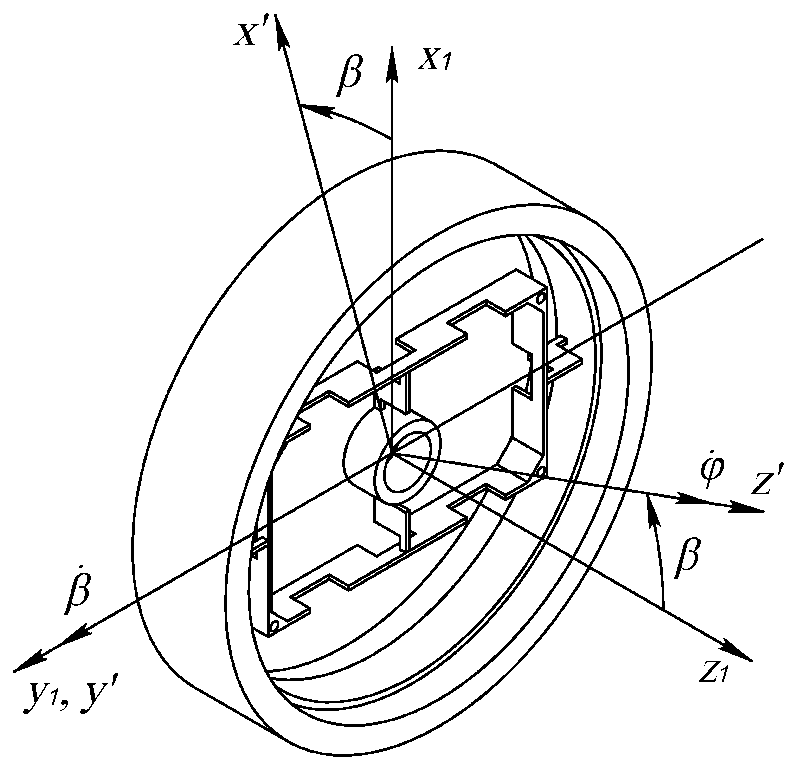



Рис. 3.8. Положение ротора относительно первого кольца

Тела, входящие в систему, имеют массовые характеристики. Зададим их через тензоры инерции.

Тензор инерции вала:

(4)

Тензор инерции первого кольца:

(5)

Тензор инерции второго кольца:

(6)

Тензор инерции ротора в предположении, что он симметричен относительно оси z’:

(7)

Связь между системами координат

Для определения связи между введёнными системами координат найдём матрицы последовательных поворотов, которые получим, проецируя оси «новых» систем координат на оси «старых».

Одна матрица поворота описывает поворот системы координат вокруг какой-либо из её осей на определённый угол. Таким образом, каждая из матриц поворота описывает поворот какого-либо элемента механической системы ДНГ на определённый угол вокруг одной из осей связанной с ним системы координат.

Наклон вала относительно основания на угол α₂:

(8)

Наклон вала относительно основания на угол β ₂:

(9)

Поворот колец вместе с валом относительно основания на угол φ:

(10)

Наклон первого кольца относительно вала и наклон ротора относительно второго кольца на угол α:

(11)

Наклон второго кольца относительно вала и наклон ротора относительно первого кольца на угол β:

(12)

Наклон маховика относительно вала на угол α₁:

(13)

Наклон маховика относительно вала на угол β₁:

(14)