лабораторной работе №3 ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ. Лаба 2 Тоэ. Исследование свободных процессов
 Скачать 1.56 Mb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) Кафедра ФИБС ОТЧЕТ по лабораторной работе №3 по дисциплине «Теоретические основы электротехники» Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Студенты гр. 0584: Подсевалов Ю.В. Преподаватель: Евдакова Е. Г. Санкт-Петербург 2022 Лабораторная Работа № 3 ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLС-контура по осциллограммам. В работе предлагается исследовать свободные процессы в цепях. Цепи возбуждаются короткими импульсами тока io (t), заряжающими конденсатор С. В паузах между импульсами конденсатор разряжается; цепь находится в свободном режиме, так как в это время источник возбуждения отключен (i0 = 0). Напряжения на элементах цепи осциллографируются. Поведение линейных цепей описывается линейными дифференциальными уравнениями; при этом вид свободного процесса определяется корнями pk характеристического уравнения (собственными частотами цепи). При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости цепи Y (р ), т. е. как корни уравнения Y (р) = 0. У цепи первого порядка одна собственная частота р, вещественная и отрицательная; свободный процесс описывается затухающей экспонентой: u(t) = Aept = Ae-αe=Ae-t/τ где u - напряжение на каком-либо элементе цепи; t - время; α - постоянная затухания; т — постоянная времени; А - постоянная интегрирования. У цепи второго порядка две собственные частоты р1,2 могут быть вещественными (простыми или кратными) или комплексно-сопряженными. В случае вещественных простых собственных частот: 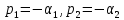 свободный процесс описывается суммой двух экспонент: 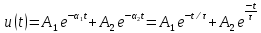 и называется апериодическим. Временная диаграмма процесса для случая А - - А . и г, > т 2 приведена на рис. 3.1, б; штрихами показаны отдельные составляющие процесса. 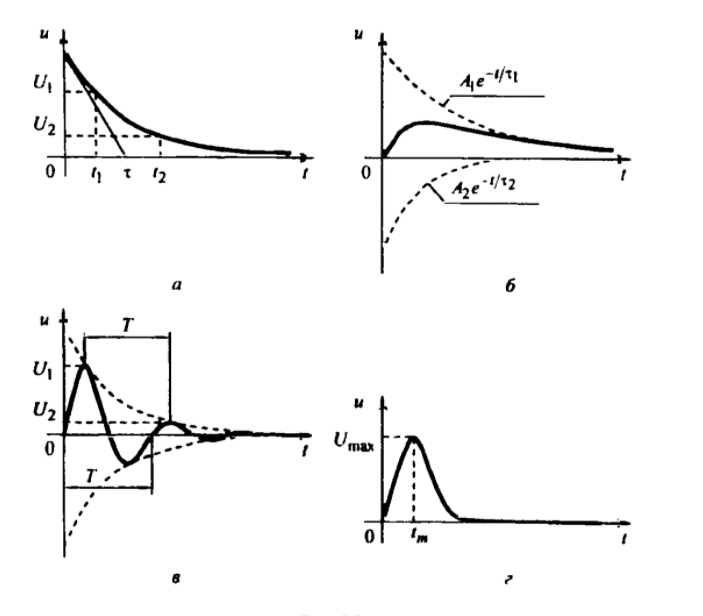 Рис. 3.1 В случае комплексно-сопряженных собственных частот 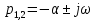 свободный процесс описывается выражением 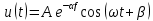 и называется колебательным; частота затухающих колебаний 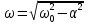 .Временная диаграмма процесса приведена на рис. 3.1, в. В случае вещественных кратных собственных частот 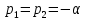 свободный процесс описывается выражением 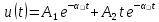 и называется критическим (предельным апериодическим). Временная диаграмма процесса для случая A1 = 0 приведена на рис. 3.1, г, где tm – момент достижения максимума. Экспериментальные исследования ГС, расположенный на приборном стенде, переведите в режим генера- ции напряжения прямоугольной формы. Выполните предварительную на- стройку осциллографа: рабочий канал - I, масштаб по вертикали — 2 В/дел, синхронизация - внутренняя по каналу I, масштаб по горизонтали - 0,2 мс/дел. Используя осциллограф, установите амплитуду и период сигнала ГС соответственно Um = 8 В и Гс = 1,2 мс. Подключите ГС ко входу генератора импульсов на лабораторной плате. 3.2.1. Исследование свободных процессов в цепи первого порядка Соберите схему, показанную на рис. 3.1, а (С = 0,02 мкФ, R = 5 кОм, источником тока i0 (t) является генератор импульсов). Снимите осциллограмму напряжения на конденсаторе, зафиксировав на ней один полный полупериод сигнала 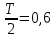 мс (ручку временной развертки осциллографа рекомендуется установить при этом в положение 0,1 мс/дел).По снятой осциллограмме определите собственную частоту цепи.3.2.2. Исследование свободных процессов в цепи второго порядка Соберите схему, показанную на рис. 3.1, б (С = 0,02 мкФ, L = 25 мГн). Снимите осциллограмму напряжения на резисторе при значениях R = 0,5 кОм (колебательный режим) R = 3 кОм (апериодический режим). Затем найдите такое значение R1, при котором в цепи будет наблюдаться критический режим, т. е. режим, граничный между колебательным и апериодическим. Снимите осциллограмму процесса и запишите полученное значение сопротивления R1=R1кр . В заключение установите R1 = 0 и снимите осциллограмму напряжения на конденсаторе. По осциллограммам, снятым при R1 =0,5 кОм и R1 = R1кр определите собственные частоты цепи. Найдите также согласно (3.10) добротность контура при R1 = 0 и R1 = 0,5 кОм. Осциллограмма напряжения на конденсаторе (R = 0 кОм)  Осциллограммы свободных процессов в цепи второго порядка в апериодическом режиме (R = 3 кОм)  Осциллограммы свободных процессов в цепи второго порядка в колебательном режиме (R = 0,5 кОм) 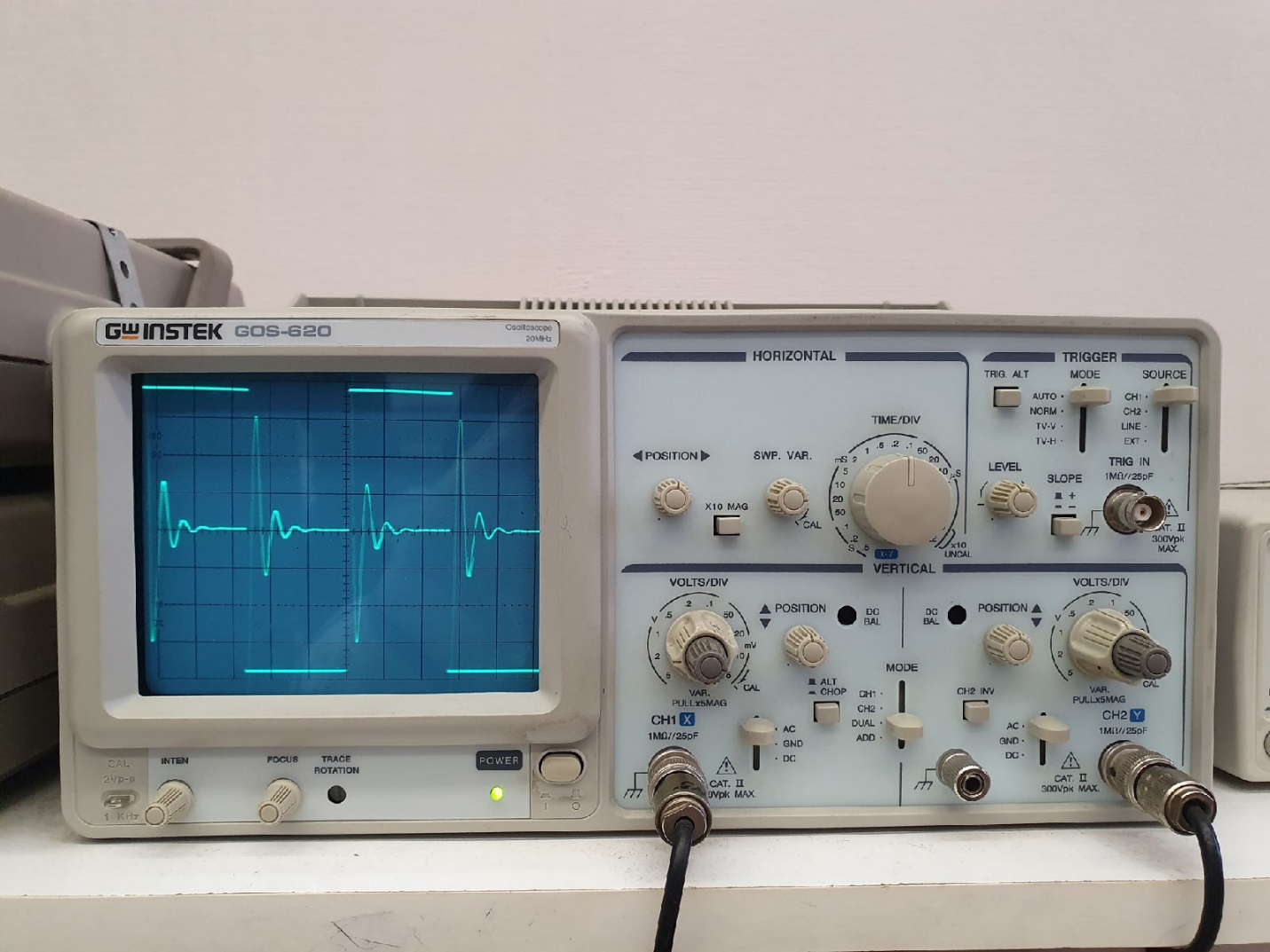 Осциллограммы свободных процессов в цепи второго порядка в критическом режиме (R = 1,5 кОм)  3.2.3. Исследование свободных процессов в цепи третьего порядка Соберите схему, показанную на рис. 3.1, в (С=0,02мкФ, R= 5 кОм, R1= 1 кОм, L = 25 мГн). Снимите осциллограмму напряжения на входе цепи. 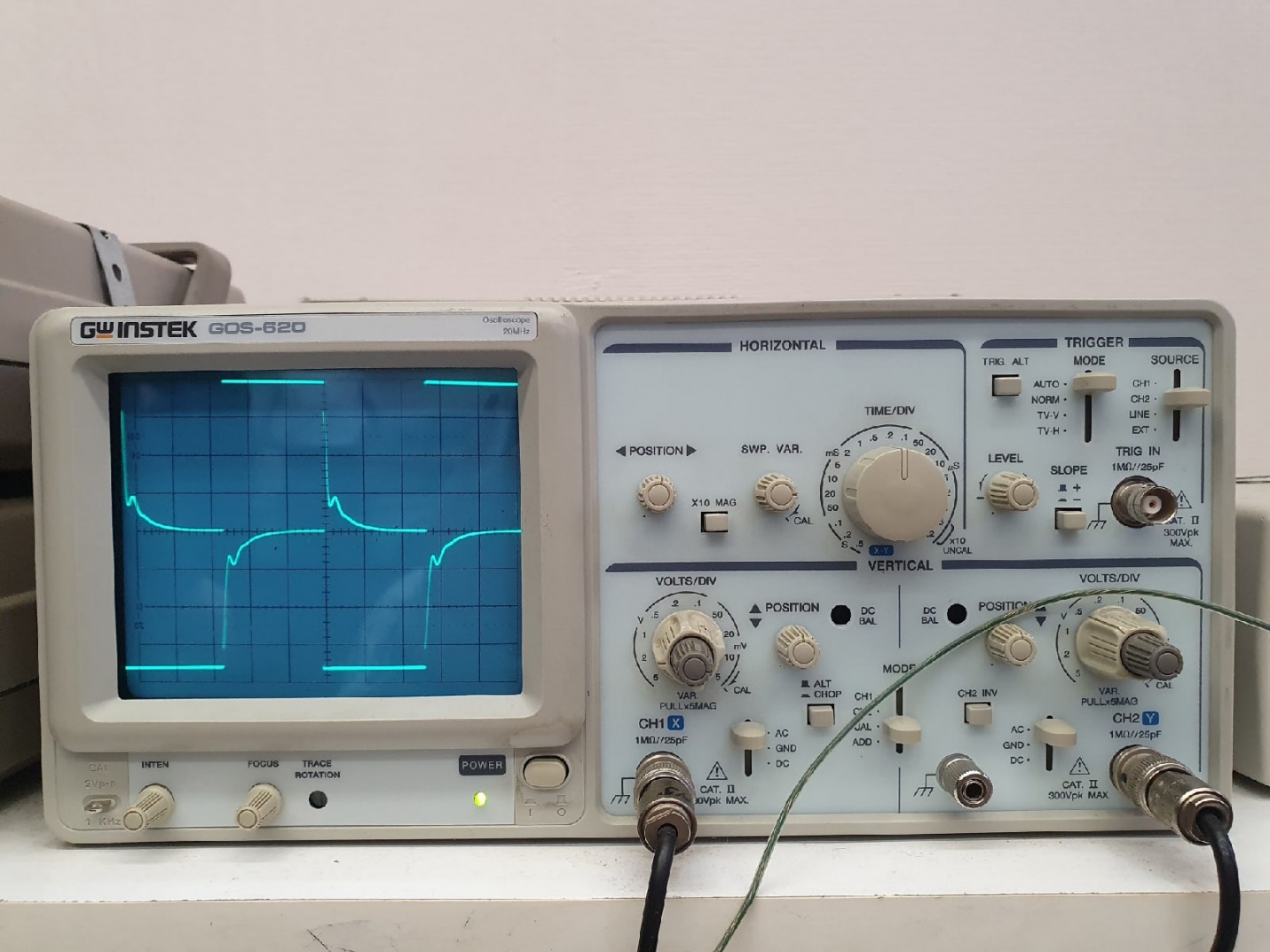 Ответы на контрольные вопросы 1. Каким аналитическим выражением описывается переходный процесс в цепи первого порядка? 𝑢(𝑡)=𝐴𝑒−𝛼𝑡 , где А – постоянная, α – постоянная затухания. 2. Как по осциллограмме определить собственную частоту цепи первого порядка? Соответствует ли она теоретическому расчету по (3.1)? Либо по формуле 𝛼=1𝜏=ln𝑈1𝑈2∆𝑡, (U1, U2, Δt = t2-t1 определяем по осциллограмме), либо используя метод подкасательной (проводим подкасательную и находим ее проекцию на ось Х, найденное значение – τ ). Как видно из пункта 1 обработки результатов экспериментальное значение примерно равно теоретическому. 3. Какими аналитическими выражениями (в общем виде) описываются графики процессов во всех исследуемых цепях второго порядка? Как определить по осциллограмме, снятой при R1 = 0,5 кОм, собственные частоты цепи второго порядка? Критический режим: 𝑢(𝑡)=𝐴1𝑒−𝛼𝑡+𝐴2𝑡𝑒−𝛼𝑡. Колебательный режим: 𝑢(𝑡)=𝐴𝑒−𝛼𝑡cos(𝜔𝑡+𝛽). Апериодический режим: 𝑢(𝑡)=𝐴1𝑒−𝛼1𝑡+𝐴2𝑒−𝛼2𝑡. Чтобы определить собственные частоты второго порядка по осциллограмме нужно найти значения U1, U2, Δt = Т. Далее по формулам находим w0 и Q: 𝜔0=2𝜋𝑇, 𝑄= 𝜋ln𝑈1𝑈2 . Используя полученные значения найти собственные частоты по формуле 𝑝1,2=−𝑤02𝑄(1±√1−4𝑄2). 4. Каким аналитическим выражением описывается полученный график свободного процесса в цепи третьего порядка? 𝑢(𝑡)= 𝐴1𝑒−𝛼1𝑡+𝐴2𝑒−𝛼2𝑡+𝐴3𝑒−𝛼3𝑡 5. Каковы теоретические значения собственных частот цепи третьего порядка? Соответствует ли им осциллограмма и почему? р1 = -10^4 p2,3 = -2,5*10^4 ± 6*10^4j Значение частот соответствует осциллограмме, тк при сложении экспонент с такими показателями получается соответствующий график. |