Вариант 30
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 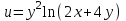
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 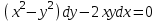
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 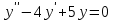 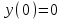 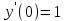 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
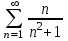
|
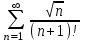
|
5.
|
Написать пять членов разложения функции 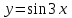 в ряд Маклорена. в ряд Маклорена.
|
Вариант 31
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 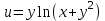
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 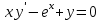
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 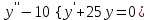 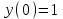 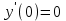 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
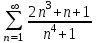
|
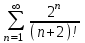
|
5.
|
Найти область сходимости степенного ряда: 
|
Вариант 32
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 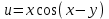
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 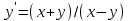
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 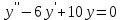 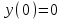 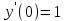 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
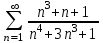
|
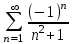
|
5.
|
Найти область сходимости степенного ряда: 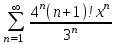
|
Вариант 33
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 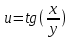
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 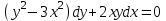
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 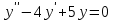 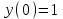 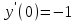 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|

|
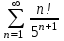
|
5.
|
Найти область сходимости степенного ряда: 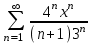
|
Вариант 34
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 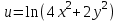
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 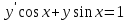
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 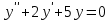 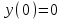 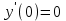 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
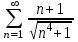
|
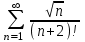
|
5.
|
Найти область сходимости степенного ряда: 
|
Вариант 35
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 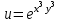
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 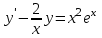
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 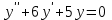 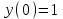 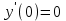 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
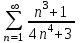
|
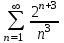
|
5.
|
Найти область сходимости степенного ряда: 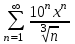
|
Вариант 36
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 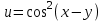
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 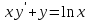
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 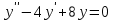 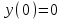 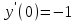 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|
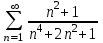
|
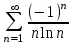
|
5.
|
Найти область сходимости степенного ряда: 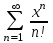
|
Вариант 37
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 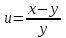
|
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 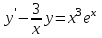
|
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям:  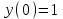 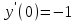 . .
|
|
4.
|
Исследовать числовые ряды на сходимость.
|
|
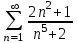
|
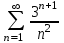
|
|
5.
|
Найти область сходимости степенного ряда: 
|
|
Вариант 38
1.
|
Найти все частные производные второго порядка заданной функции двух переменных, доказав при этом равенство смешанных производных. 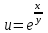
|
2.
|
Определить тип дифференциального уравнения первого порядка и найти его общее решение: 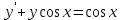
|
3.
|
Определить частное решение линейного дифференциального уравнения второго порядка с постоянными коэффициентами, удовлетворяющее заданным начальным условиям: 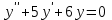 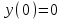 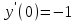 . .
|
4.
|
Исследовать числовые ряды на сходимость.
|

|
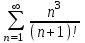
|
5.
|
Написать пять членов разложения функции 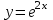 в ряд Маклорена. в ряд Маклорена.
| |
 Скачать 406.46 Kb.
Скачать 406.46 Kb.