Итоговая проверочная работа на промежуточной аттестации
по математике в 10 классе (базовый уровень)
1 вариант.
1.Вычислить: 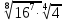
2.Решить уравнение: 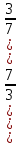
3.Решить неравенство: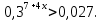
1)(-∞;-1); 2)(-1;∞); 3)(-1;1).
4. Плоскость 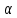 проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения. проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения.
1)трапеция; 2)параллелограмм; 3)треугольник.
5.Вычислить: 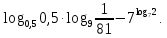
6.Назвать сумму корней уравнения: 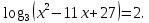
7.Решить неравенство: 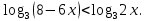
1)(-∞;1); 2)(1;∞); 3)(-1;1).
8. Измерения прямоугольного параллелепипеда равны 12, 9 и 8 м. Найдите диагональ параллелепипеда.
9.Вычислить: 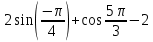 tg2 tg2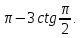
1)0,5-√2; 2)√2-0,5; 3)1,2+√2.
10.Решить уравнение: tg 2x+1=0.
1)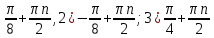
11.Решить неравенство: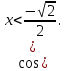
1) 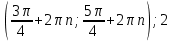 ) )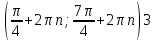 ) )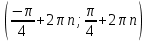
12. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по теме "Ботаника". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопрос по теме "Ботаника".
Итоговая проверочная работа на промежуточной аттестации
по математике в 10 классе (базовый уровень)
2 вариант.
1.Вычислить: 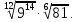
2.Решить уравнение: 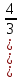
3. Решить неравенство: 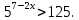
1)(-∞;2); 2)(-2;∞); 3)(-2;2).
4. Плоскость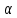 пересекает только боковые рёбра параллелепипеда. Определите вид сечения. пересекает только боковые рёбра параллелепипеда. Определите вид сечения.
1)трапеция; 2)параллелограмм; 3)треугольник.
5.Вычислить: 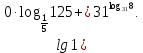
6. Назвать сумму корней уравнения: 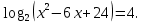
7. 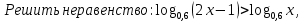
1)(-∞;1); 2)(1;∞); 3)(-1;1).
8.Измерения прямоугольного параллелепипеда равны 6, 4 и 12 м. Найдите диагональ параллелепипеда.
9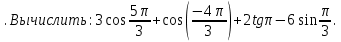
1)0,5-√3; 2)√3-3; 3)1-3√3.
10.Решить уравнение: : сtg 2x-1=0.
1)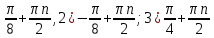
11.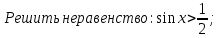
1) 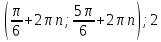 ) )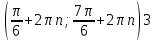 ) )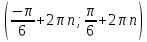
12. В сборнике билетов по биологии всего 55 билетов, в 22 из них встречается вопрос по теме "Ботаника". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Ботаника".

Спецификация
итоговой проверочной работы на промежуточной аттестации
по математике в 11 классе (базовый уровень)
Выполнение заданий итоговой проверочной работы на промежуточной аттестации свидетельствует о наличии у участника работы общематематических умений, необходимых человеку в современном обществе. Задания проверяют базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную на графиках и в таблицах, использовать простейшие вероятностные и статистические модели, ориентироваться в простейших геометрических конструкциях. В работу включены задания базового уровня по всем основным предметным разделам: геометрия (планиметрия и стереометрия), алгебра, начала математического анализа, теория вероятностей и статистика.
Тексты заданий предлагаемой модели итоговой проверочной работы в целом соответствуют формулировкам, принятым в учебниках и учебных пособиях, включенным в Федеральный перечень учебников, рекомендуемых Министерством образования и науки РФ к использованию при реализации имеющих государственную аккредитацию образовательных программ основного общего и среднего общего образования.
Структура работы.
Итоговая проверочная работа состоит из одной части, включающей 12 заданий с кратким ответом базового уровня сложности. Все задания направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях.
Ответом к каждому из заданий 1–12 является целое число или конечная десятичная дробь, или последовательность цифр. Задание с кратким ответом считается выполненным, если верный ответ записан в бланке ответов № 1 в той форме, которая предусмотрена инструкцией по выполнению задания.
В итоговой проверочной работе проверяется следующий учебный материал:
Алгебра и начала анализа, 10–11 классы;
Теория вероятностей и статистика, 7–9 классы;
Геометрия, 7–11 классы.
Распределение заданийпо содержательным разделам курсаматематики
Содержательные разделы
|
Количество заданий
|
Максимальный первичный балл
|
Алгебра и начала математического анализа
|
9
|
9
|
Геометрия
|
2
|
2
|
Элементы комбинаторики, статистики и теории вероятностей
|
1
|
1
|
Итого
|
12
|
12
|
Содержание и структура итоговой проверочной работы дают возможность достаточно полно проверить комплекс умений и навыков по предмету:
уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни;
уметь выполнять вычисления и преобразования;
уметь решать уравнения и неравенства;
уметь выполнять действия с функциями;
уметь выполнять действия с геометрическими фигурами;
уметь строить и исследовать математические модели.
Распределение заданий по видам проверяемых умений и способам действий
Проверяемые умения и способы действий
|
Количество заданий
|
Максимальный первичный балл
|
Уметь выполнять вычисления и преобразования
|
3
|
3
|
Уметь решать уравнения
|
3
|
3
|
Уметь решать неравенства
|
3
|
3
|
Уметь выполнять действия с геометрическими фигурами
|
2
|
2
|
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни
|
1
|
1
|
Итого
|
12
|
12
|
Распределение заданий по уровнюсложности.
Итоговая проверочная работа содержит задания только базового уровня сложности.
Продолжительность работы.
На выполнение итоговой проверочной работы на промежуточной аттестации отводится 45 минут..
Система оценивания.
Правильное решение каждого из заданий 1–12 оценивается 1 баллом. Задание считается выполненным верно, если обучающийся дал правильный ответ в виде целого числа или конечной десятичной дроби, или последовательности цифр.
Максимальный первичный балл за всю работу – 12.
На основе баллов, выставленных за выполнение всех заданий работы, подсчитывается общий балл, который переводится в отметку по пятибалльной шкале.
Отметка по пятибалльной шкале
|
«2»
|
«3»
|
«4»
|
«5»
|
Суммарный балл
|
0-4 балла
|
5-7 баллов
|
8-10 баллов
|
11-12 баллов
|
Кодификатор элементов содержания
для проведения итоговой проверочной работы на промежуточной аттестации
по математике в 11 классе (базовый уровень)
Кодификаторявляется систематизированным перечнем требований к уровню подготовки выпускников и проверяемых элементов содержания, в котором каждому объекту соответствует определённый код.
В первом столбце таблицы указаны коды разделов и тем. Во втором столбце указан код элемента содержания, для которого создаются проверочные задания.
№
|
Код контролиру- емого элемента
|
Элементы содержания, проверяемые заданиями экзаменационной работы
|
1
|
|
Алгебра
|
1.1
|
|
Числа, корни и степени
|
1.1.1
|
Целые числа
|
1.1.2
|
Степень с натуральным показателем
|
1.1.3
|
Дроби, проценты, рациональные числа
|
1.1.4
|
Степень с целым показателем
|
1.1.5
|
Корень степени n > 1 и его свойства
|
1.1.6
|
Степень с рациональным показателем и её свойства
|
1.1.7
|
Свойства степени с действительным показателем
|
1.2
|
|
Основы тригонометрии
|
1.2.1
|
Синус, косинус, тангенс, котангенс произвольного угла
|
1.2.2
|
Радианная мера угла
|
1.2.3
|
Синус, косинус, тангенс и котангенс числа
|
1.2.4
|
Основные тригонометрические тождества
|
1.2.5
|
Формулы приведения
|
1.2.6
|
Синус, косинус и тангенс суммы и разности двух углов
|
1.2.7
|
Синус и косинус двойного угла
|
1.3
|
|
Логарифмы
|
1.3.1
|
Логарифм числа
|
1.3.2
|
Логарифм произведения, частного, степени
|
1.3.3
|
Десятичный и натуральный логарифмы, число е
|
1.4
|
|
Преобразования выражений
|
1.4.1
|
Преобразования выражений, включающих арифметические операции
|
|
1.4.2
|
Преобразования выражений, включающих операцию возведения в степень
|
1.4.3
|
Преобразования выражений, включающих корни
натуральной степени
|
1.4.4
|
Преобразования тригонометрических выражений
|
1.4.5
|
Преобразование выражений, включающих операцию логарифмирования
|
1.4.6
|
Модуль (абсолютная величина) числа
|
2
|
|
Уравнения и неравенства
|
2.1
|
|
Уравнения
|
2.1.1
|
Квадратные уравнения
|
2.1.2
|
Рациональные уравнения
|
2.1.3
|
Иррациональные уравнения
|
2.1.4
|
Тригонометрические уравнения
|
2.1.5
|
Показательные уравнения
|
2.1.6
|
Логарифмические уравнения
|
2.1.7
|
Равносильность уравнений, систем уравнений
|
2.2
|
|
Неравенства
|
2.2.1
|
Квадратные неравенства
|
2.2.2
|
Рациональные неравенства
|
2.2.3
|
Показательные неравенства
|
2.2.4
|
Логарифмические неравенства
|
2.2.5
|
Системы линейных неравенств
|
2.2.6
|
Системы неравенств с одной переменной
|
2.2.7
|
Равносильность неравенств, систем неравенств
|
2.2.8
|
Использование свойств и графиков функций при решении неравенств
|
2.2.9
|
Метод интервалов
|
2.2.10
|
Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем
|
3
|
|
Геометрия
|
3.1
|
|
Планиметрия
|
3.1.1
|
Треугольник
|
3.1.2
|
Параллелограмм, прямоугольник, ромб, квадрат
|
3.1.3
|
Трапеция
|
3.1.4
|
Окружность и круг
|
3.1.5
|
Окружность, вписанная в треугольник, и окружность,
описанная около треугольника
|
3.1.6
|
Многоугольник. Сумма углов выпуклого многоугольника
|
|
3.1.7
|
Правильные многоугольники. Вписанная окружность и
описанная окружность правильного многоугольника
|
3.2
|
|
Прямые и плоскости в пространстве
|
3.2.1
|
Пересекающиеся, параллельные и скрещивающиеся прямые; перпендикулярность прямых
|
3.2.2
|
Параллельность прямой и плоскости, признаки и свойства
|
3.2.3
|
Параллельность плоскостей, признаки и свойства
|
3.2.4
|
Перпендикулярность прямой и плоскости, признаки и свойства; перпендикуляр и наклонная; теорема о трёх
перпендикулярах
|
3.2.5
|
Перпендикулярность плоскостей, признаки и свойства
|
3.2.6
|
Параллельное проектирование. Изображение
пространственных фигур
|
3.3
|
|
Многогранники
|
3.3.1
|
Призма, её основания, боковые рёбра, высота, боковая
поверхность; прямая призма; правильная призма
|
3.3.2
|
Параллелепипед; куб; симметрии в кубе, в параллелепипеде
|
3.3.3
|
Пирамида, её основание, боковые рёбра, высота, боковая поверхность; треугольная пирамида; правильная пирамида
|
3.3.4
|
Сечения куба, призмы, пирамиды
|
3.3.5
|
Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)
|
3.4
|
|
Тела и поверхности вращения
|
3.4.1
|
Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
|
3.4.2
|
Конус. Основание, высота, боковая поверхность,
образующая, развертка
|
3.4.3
|
Шар и сфера, их сечения
|
3.5
|
|
Измерение геометрических величин
|
3.5.1
|
Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности
|
3.5.2
|
Угол между прямыми в пространстве; угол между прямой и плоскостью, угол между плоскостями
|
3.5.3
|
Длина отрезка, ломаной, окружности,периметр
многоугольника
|
3.5.4
|
Расстояние от точки до прямой, от точки до плоскости;
расстояние между параллельными и скрещивающимися прямыми, расстояние между параллельными плоскостями
|
3.5.5
|
Площадь треугольника, параллелограмма, трапеции, круга, сектора
|
3.5.6
|
Площадь поверхности конуса, цилиндра, сферы
|
3.5.7
|
Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
|
4
|
|
Элементы комбинаторики, статистики и теории вероятностей
|
4.1
|
|
Элементы комбинаторики
|
4.1.1
|
Поочередный и одновременный выбор
|
4.1.2
|
Формулы числа сочетаний и перестановок. Бином Ньютона
|
4.2
|
|
Элементы статистики
|
4.2.1
|
Табличное и графическое представление данных
|
4.2.2
|
Числовые характеристики рядов данных
|
4.3
|
|
Элементы теории вероятностей
|
4.3.1
|
Вероятности событий
|
4.3.2
|
Примеры использования вероятностей и статистики при
решении прикладных задач
|
Кодификатор требований к уровню подготовки обучающихся
для проведения итоговой проверочной работы на промежуточной аттестации
по алгебре в 9 классе
Кодификатор является систематизированным перечнем требований к уровню подготовки выпускников и проверяемых элементов содержания, в котором каждому объекту соответствует определённый код.
В первом столбце таблицы указаны коды разделов, на которые разбиты требования к уровню подготовки по математике. Во втором столбце указан код умения, для проверки которого создаются проверочные задания. В третьем столбце сформулированы требования к уровню подготовки выпускников.
№
|
Код контролиру- емого требования (умения)
|
Требования (умения), проверяемые заданиями итоговой проверочной работы
|
1
|
|
Уметь выполнять вычисления и преобразования
|
1.1
|
Выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма
|
1.2
|
Вычислять значения числовых и буквенных выражений,
осуществляя необходимые подстановки и преобразования
|
1.3
|
Проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции
|
2
|
|
Уметь решать уравнения и неравенства
|
2.1
|
Решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы
|
2.2
|
Решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод
|
2.3
|
Решать рациональные, показательные и логарифмические
неравенства, их системы
|
3
|
|
Уметь выполнять действия с функциями
|
3.1
|
Определять значение функции по значению аргумента при
|
|
|
различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций
|
3.2
|
Вычислять производные и первообразные элементарных
функций
|
3.3
|
Исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функции
|
4
|
|
Уметь выполнять действия с геометрическими фигурами, координатами и векторами
|
4.1
|
Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей)
|
4.2
|
Решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении стереометрических задач планиметрические факты и методы
|
4.3
|
Определять координаты точки; проводить операции над
векторами, вычислять длину и координаты вектора, угол между векторами
|
5
|
|
Уметь строить и исследовать простейшие математические
|
|
модели
|
|
5.1
|
Моделировать реальные ситуации на языке алгебры, составлять
|
|
|
уравнения и неравенства по условию задачи; исследовать
|
|
|
построенные модели с использованием аппарата алгебры
|
|
5.2
|
Моделировать реальные ситуации на языке геометрии,
|
|
|
исследовать построенные модели с использованием
|
|
|
геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин
|
|
|
|
|
|
|
|
5.3
|
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, познавать логически некорректные рассуждения
|
|
|
|
|
|
|
|
5.4
|
Моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий
|
|
|
|
|
|
|
6
|
|
Уметь использовать приобретенные знания и умения в
|
|
практической деятельности и повседневной жизни
|
|
6.1
|
Анализировать реальные числовые данные, информацию
|
|
|
статистического характера; осуществлять практические расчеты
|
|
|
по формулам; пользоваться оценкой и прикидкой при
|
|
|
практических расчетах
|
|
6.2
|
Описывать с помощью функций различные реальные
|
|
|
зависимости между величинами и интерпретировать их
|
|
|
графики; извлекать информацию, представленную в таблицах, на диаграммах и графиках
|

|
|
| |
 Скачать 170.54 Kb.
Скачать 170.54 Kb.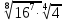
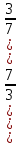
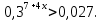
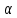 проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения.
проходит через диагональ основания параллелепипеда и середину одной из сторон верхнего основания. Определите вид сечения.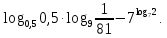
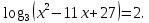
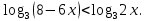
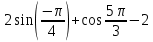 tg2
tg2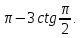
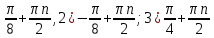
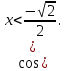
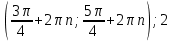 )
)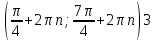 )
)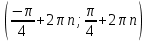
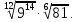
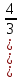
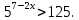
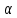 пересекает только боковые рёбра параллелепипеда. Определите вид сечения.
пересекает только боковые рёбра параллелепипеда. Определите вид сечения.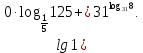
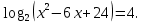
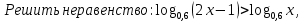
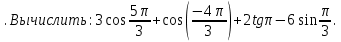
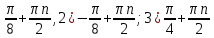
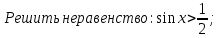
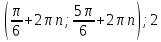 )
)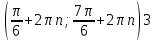 )
)