|
|
Лабораторная работа. ЛР 7.2 Колчева В.С, ЗМ-221. Измерение радиуса кривизны линзы методом интерференционных колец ньютона
Два условия возникновения интерференции волн:
1- Когерентность волн, такое наложение двух волн, при котором в различных точках пространства колебания световых векторов волн происходит синхронно и возникают устойчивые во времени максимумы и минимумы интенсивности. Это означает – разность фаз двух волн постоянна во времени:
∆𝝋 = 𝝋𝟐 − 𝝋𝟏 = 𝒄𝒐𝒏𝒔𝒕 – условие когерентности базовое
Следствие: учитывая, что фаза равна 𝜑 = (𝜔𝑡 − 𝑘𝑥 + 𝜙0), 𝑎 𝑘 = 2𝜋/𝜆 получаем, что волны когерентны, если у них одинаковы частоты и разность начальных фаз постоянна:
𝝎𝟏 = 𝝎𝟐; (𝝓𝟎𝟏 − 𝝓𝟎𝟐) = 𝒄𝒐𝒏𝒔𝒕 – условие когерентности удобное для анализа
2 - Идентичная поляризация двух волн, это означает, что колебания светового вектора происходят в одном направлении, или в близких направлениях.
Условия максимума и минимума интенсивности интерференционной картины
Оптическая длина пути, оптическая разность хода волн
В вакууме скорость света (с) всегда постоянна и равна с = 3 ∙ 108, м/с. В среде скорость света (V) меньше, чем в вакууме, Отношение этих скоростей называется показателем преломления среды
𝑛 = 𝑐/𝑉 , (2)
Например, в стекле (n=1,5) скорость света в полтора раза меньше, чем в вакууме. Таким образом, для преодоления одного и того-же расстояния свету в стекле понадобится в n раз больше времени, т.е. в 1,5 раза больше времени. Чем в вакууме. Чтобы упростить расчеты при анализе интерференционных и дифракционных явлений вводят понятие оптической длины пути:
Оптическая длина пути - это расстояние, которое прошел бы свет в вакууме за то время, которое он затратил на прохождение заданного пути в веществе. Оптическая длина пути в n раз больше расстояния, пройденного светом в веществе с показателем преломления n:
𝐿ОПТ = 𝑛𝐿 (3)
Например, свет в стекле с показателем преломления n=1,5 прошел расстояние L Определить оптическую длину пути: Lопт=nL=1,5L.
Оптическая разность хода (∆) – это разность оптических путей двух интерферирующих лучей от точки их раздвоения до экрана или другого объекта, где создается интерференционная картина
∆= 𝐿ОПТ2 − 𝐿ОПТ1 (4)
Условия максимума и минимума интенсивности интерференционной картины, записанное через оптическую разность хода лучей - (∆).
Пусть происходит интерференция двух когерентных волн с одинаковыми амплитудами световых векторов Em1= Em2= Em. Если электромагнитные волны приходят в точку наблюдения в фазе, то при их наложении световые вектора волн будут направлены в одну сторону и будут складываются и общая (результирующая) амплитуда будет удвоена (EРЕЗ= Em1+ Em2= 2Em), а интенсивность результирующей волны будет в 4 раза больше интенсивности исходной волны, т.к. интенсивность пропорциональна квадрату амплитуды, IРЕЗ= 4I
4(Em)2. В этих точках будут наблюдаться максимумы, т.е. наиболее яркие линии интерференционной картины (максимумы на рисунке 3).
Если волны придут в точку наблюдения в противофазе, то световые вектора будут компенсировать друг друга, они будут направлены в разные стороны и результирующий вектор будет равен разности исходных световых векторов (EРЕЗ= Em1– Em2= 0). В точке наблюдения света не будет – минимуму интенсивности.
Учитывая это и переходя от разности фаз к разности оптических путей получаем условие максимума и минимума интенсивности интерференционной картины, записанное через оптическую разность хода лучей - (∆).
∆= ±𝒎 ∙ 𝝀𝟎, (m= 0, 1, 2, …) – условие максимума (5)
 
𝟎
𝚫 = ± (𝒎 + 𝟏) ∙ 𝝀 , (m= 0, 1, 2, …) – условие минимума (6)
Условие максимума (5): при интерференции 2-х когерентных волн в точке наблюдения будет наблюдаться интерференционный максимум, если оптическая разность хода этих волн равна целому числу волн (волны приходят в точку наблюдения в фазе). Условие минимума (6): при интерференции 2-х когерентных волн в точке наблюдения будет наблюдаться интерференционный минимум, если оптическая разность хода этих волн равна полуцелому числу волн (волны приходят в точку наблюдения в противофазе).

Идеальную интерференционную картину от двух световых волн представляет рисунок 3, который иллюстрирует условия максимума и минимума при интерференции. На нем по оси абсцисс отложена оптическая разность хода двух волн, по оси ординат интенсивность результирующей волны
I. Как видно из рисунка, при оптической разности хода (ОРХ) равной нулю наблюдается максимум интенсивности при изменении ОРХ на величину равную длине волны снова возникает максимум, а при изменении ОРХ на пол длины волны попадаем в минимум
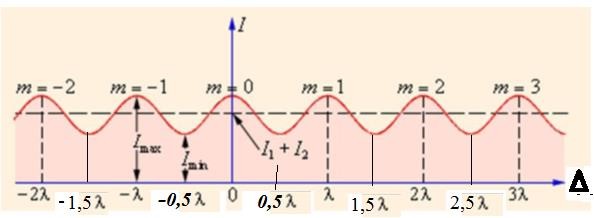
Рисунок 3 - Распределение интенсивности в интерференционной картине в зависимости от величины оптической разности хода. Целое число m – порядок интерференционного максимума
|
|
|
 Скачать 0.66 Mb.
Скачать 0.66 Mb.



