Беседин. Как возникли различные системы счисления
 Скачать 66.21 Kb. Скачать 66.21 Kb.
|
|
Индивидуальный итоговый проект по информатике (информатика) по теме «Как возникли различные системы счисления» Автор работы: Беседин Антон Студент группы чс-11 Руководитель проекта: Самохвалова Ольга, учитель информатики Курск 2021 Оглавление Введение……………………………………………………………………………………3 Глава 1 Математические основы информатики…………………………………………5 Общие сведения о системах счисления…………………………………………..5 Двоичная система счисления……………………………………………………..6 Восьмеричная система счисления………………………………………………..7 Шестнадцатеричная система счисления…………………………………………8 Двоичная арифметика……………………………………………………………..9 Заключение…………………………………………………………………………………11 Вывод……………………………………………………………………………………….12 Литература…………………………………………………………………………………13 Введение Все дети рождаются исследователями. Исследовательское поведение для ребенка – главный источник получения представлений об окружающем мире. В ходе исследования учащийся не только открывает для себя и других нечто новое, но и развивает такие способности и умения, которые необходимы сегодня каждому успешному человеку: активность, самостоятельность, умение ориентироваться в быстро меняющемся потоке информации, развитые интеллектуальные, коммуникативные, творческие способности, умения размышлять, сопоставлять разные факты, точки зрения, формулировать и аргументировать собственную позицию. Целевая установка формирования у учащихся названных качеств обозначена в Федеральном государственном образовательном стандарте среднего (полного) общего образования. Актуальность Актуальность работы состоит в следующем: сегодня четко обозначена необходимость знаний по системам счисления как части фундаментальной информатики. Эти знания применяются в различных сферах. Прежде всего, это арифметические операции в цифровых электронных устройствах, которые предоставляют человеку быстрые числовые расчеты практически в любой сфере деятельности. Цель работы - познакомиться с различными системами счисления и найти их применение в жизни. Задачи: - рассмотреть виды систем счисления и историю их развития Новизна Через исследование и решение задач мы получаем новую для себя информацию по истории развития числа. В процессе работы мы можем почувствовать себя в роли исследователей, познавая самостоятельно для себя новые разделы математики. Гипотеза Самостоятельно расширить свои знания о числе, сформировать для себя необходимые навыки записи и перевода чисел в различных системах счисления В своей работе я использовал разные методы исследования: - работа с источниками информации; - применил примеры систем счисления из жизни; - сделал выводы; Современный человек каждый день запоминает номера машин и телефонов, в магазине подсчитывает стоимость покупок, ведет семейный бюджет и т. д. Числа, цифры они с нами везде. Люди всегда считали и записывали числа, даже пять тысяч лет назад. Но записывали они их совершенно по-другому, по другим правилам. Но в любом случае число изображалось с помощью любого или нескольких символов, которые называются цифрами. Математические основы информатики Работа имеет интегрированный межпредметный характер, где раскрываются связи двух предметов: математики и информатики. Число́ — основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Возникнув ещё в первобытном обществе из потребностей счета, понятие числа с развитием науки значительно расширилось. 1.1. Общие сведения о системах счисления Система счисления – это способ представления чисел и соответствующие ему правила действий над числами. Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Так появилась система счисления. Все системы счисления делятся на две большие группы: позиционные и непозиционные Система счисления: даёт представления множества чисел (целых или вещественных); даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление); отражает алгебраическую и арифметическую структуру чисел. Мы не можем писать числа так, как нам вздумается - нас должны понимать другие люди. Поэтому необходимо ещё использовать и определенные правила их записи Системы счисления подразделяются на: позиционные непозиционные В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любаяпозиционнаясистемахарактеризуетсясвоимоснованием. Основание позиционной системы счисления - это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число - два, три, четыре, шестнадцать и т.д. Следовательно, возможно бесконечное множество позиционных систем. Примеры позиционной системы счисления - двоичная, десятичная, восьмеричная, шестнадцатеричная системы счисления и т. д. Непозиционная система счисления – это такая система счисления, у которой количественный эквивалент («вес») цифры не зависит от ее местоположения в записи числа. К таким системам относятся: древнеегипетская, римская, алфавитная, древнегреческая и т. д. Двоичная система счисления Двоичная система счисления — позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов (0 и 1). Самая правая цифра числа показывает число единиц, следующая цифра - число двоек, следующая - число четверок и т.д. Как записать число в двоичной системе? Дели его на 2, в остатке будет 0 или 1. Из остатков (от последнего к первому) записывается число. Пример: Перевод из двоичной в десятичную системы счисления: 11012=1*23+1*22+0*21+1*20=8+4+1=1310 Перевод из десятичной системы счисления в двоичную:
Искомое число 100000112 Современная двоичная система была полностью описана математиком Лейбницем в XVII веке. В системе счисления Лейбница были использованы цифры 0 и 1, как и в современной двоичной системе. Как человек, увлекающийся китайской культурой, Лейбниц знал о книге Перемен и заметил, что гексаграммы соответствуют двоичным числам от 0 до 111111. Он восхищался тем, что это отображение является свидетельством крупных китайских достижений в философской математике того времени. В 1854 году английский математик Джордж Буль опубликовал знаковую работу, описывающую алгебраические системы применительно к логике, которая в настоящее время известна как Булева алгебра или алгебра логики. Его логическому исчислению было суждено сыграть важную роль в разработке современных цифровых электронных схем.Двоичная система счисления позволяет закодировать любое натуральное число - представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически. Наиболее простыми с точки зрения технической реализации являются двухпозиционные элементы, например, электромагнитное реле, транзисторный ключ. В настоящее время двоичная система счисления используется в вычислительной технике: для представления информации в двоичном коде. Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел. Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы. 1.3 Восьмеричная система счисления Восьмеричная система счисления — позиционная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7. Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Восьмеричная система счисления используется для представления машинного кода в удобном для человека виде. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной. Как записать число в восьмеричной системе? Дели его на 8, в остатке будет 0,1,2,3,4,5,6 или 7. Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения. Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнить деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего. Пример: Перевод из восьмеричной системы счисления в десятичную: 23568=2*83+3*82+5*81+6*80=2*512+3*64+5*8+6*1=1024+192+40+6=126210 Перевод из десятичной в восьмеричную систему счисления: 24510
Искомое число 3658 История: возникновение восьмеричной системы связывают с такой техникой счета на пальцах, когда считались не пальцы, а промежутки между ними (их всего восемь). 1.4 Шестнадцатеричная система счисления Позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F). При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления. Пример: Перевод из двоичной системы счисления в шестнадцатеричную (метод тетрады) 100011001012 = 0100.1100.0101 = 4C516 Перевод из шестнадцатеричной системы счисления в десятичную: FBA16=15*162+11*161+10*160=3840+176+10=402610 Перевод из десятичной системы счисления в шестнадцатеричную:
Искомое число 4D216 Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями). Шестнадцатеричный цвет — запись трёх компонентов цвета (R, G и B) в шестнадцатеричном виде. 1.5 Двоичная арифметика Чтобы овладеть любой системой счисления, надо уметь складывать и умножать в ней любые числа. Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления. Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения. Таблица сложения, вычитания и умножения для двоичной системы счисления
Сложение двоичных чисел Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего. Пример: 1011,12 + 1010,112= 10110,00 Вычитание двоичных чиселВ случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась. Пример: 10110,012 — 1001,12=1100,11 Умножение двоичных чиселРассмотрим примеры на умножение.  Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя. Рассмотрим примеры на умножение: 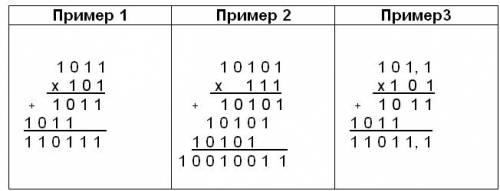 При выполнении умножения в примере 2 складываются три единицы 1+1+1=11 в соответствующем разряде пишется 1, а другая единица переносится в старший разряд. В двоичной системе счисления операция умножения сводится к сдвигам множимого и сложению промежуточных результатов. Деление двоичных чисел Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления. Рассмотрим примеры на деление:  Заключение Согласно цели исследований в работе, я познакомился с историей возникновения счета и систем счисления, изучил системы счисления, используемые в вычислительной технике, позиционные и непозиционные системы счисления и арифметические действия в различных системах счисления. Познакомившись с системами счисления, я узнал очень много нового и полезного, и считаю, что эта наука необходима для развития общества. Сложно представить мир без вычислительной техники. Ведь именно двоичная система получила широкое распространение в различных областях техники, в особенности в современных вычислительных машинах и компьютерах. Немаловажной является история развития представлений человека о системе счисления. Сложно представить, что на ранних стадиях развития общества люди не отличали совокупность двух и трех предметов. Системы счисления прошли сложный путь в своем развитии и сейчас они занимают большую нишу в области информатики. Они являются частью фундаментальной информатики. Существует огромное количество различных систем счисления и для каждой из них можно найти применение в самых различных областях человеческой деятельности. Различные системы счисления используются всегда, когда появляется потребность в числовых расчётах. В таких системах счисления наиболее важную информацию о числе содержат первые цифры. Это представляет огромный интерес в вопросах сжатия и кодирования информации. Особая актуальность изучения систем счисления связана с тем, что в будущем вполне может произойти так называемый информационный переворот, связанный с разработкой компьютеров основанных на информационной системе счисления. Так же, подводя итоги работы, можно сделать следующие выводы: 1. Позиционная система счисления состоит в использовании ограниченного числа цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры в числе на математическом языке называется разрядом. Основание позиционной системы счисления - это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе. 2. Двоичная система счисления - наиболее широко используется в компьютерах, так как один разряд двоичного числа соответствует одному биту - минимальной единице информации в компьютерной технике. 3. Для того чтобы двоичные числа, отличающиеся довольно значительной длиной, было легче воспринимать и отображать, их сжимают в восьмеричную и шестнадцатеричную системы счисления. 4. В компьютерных технологиях все виды информации кодируются только цифрами или, точнее, числами, которые представляются в двоичной системе счисления - способе представления любых чисел с помощью двух знаков (цифр) по позиционному принципу. 5. Шестнадцатеричная система счисления широко используется в низкоуровневом программировании, а также в компьютерной документации. Также, восьмеричная система счисления иногда используется в компьютерах - по видимому, чаще всего при определении прав в Unix-подобных операционных системах. Когда-то были компьютеры, в которых использовались 24-х и 36-битные слова. Шестидесятеричная система счисления широко используется при подсчёте минут и секунд. /4/. В общем, восьмеричная и шестнадцатеричная системы счисления выступают в качестве простейшего языка общения человека с ЭВМ. Я считаю, что у моей работы есть перспективы, так как тема системы счисления достаточно сложна, обширна и может использоваться в настоящей жизни. В моей работе собран и систематизирован весь материал по данной теме. Надеюсь, что моя работа найдет применение не только среди преподавателей, но и для себя. Литература 1. Учебник по информатике БосоваЛ.Л.,БосоваА. Ю. 6 издание 8 класс. 2. inf1.Info/ binarynotation 3. inf1.info/ hexadecimal 4. prog –cpp.ru/ binary –arithmetics 5. Информатика. Компьютерная техника. Компьютерные технологии. / Пособие под ред. О.И.Пушкаря.- Издательский центр "Академия", Киев, - 2001 г. 6. Учебное пособие «Арифметические основы ЭВМ и систем». Часть 1.Системы счисления 7. О.Ефимова, В.Морозова, Н.Угринович «Курс компьютерной технологии»учебное пособие для старших классов. |
