Лекция 4 ГМ. Кинематика потока в проточной части турбины. 1 Кинематика потока в проточной части. 1 Механическая модель рабочего процесса

• Название: Кинематика потока в проточной части турбины. 1 Кинематика потока в проточной части. 1 Механическая модель рабочего процесса
• Анкор: Лекция 4 ГМ.doc
• Дата: 27.08.2018
• Размер: 246.5 Kb.
• Имя файла: Лекция 4 ГМ.doc
• Тип: Лекция; #23662

Лекция 4.1 (2 часа)

Кинематика потока в проточной части турбины.

4.1 Кинематика потока в проточной части.

4.1.1 Механическая модель рабочего процесса.

Для понимания рабочего процесса турбины полезно представить себе его механическую модель. Для модели рабочего колеса надо представить себе карусель, рисунок 4.1, т. е. кольцевую вращающуюся около вертикальной оси mплощадку п. По окружающей карусель неподвижной наклонной по­верхности qс перилами сбегают люди, развивая неко­торую скорость, направленную под углом к радиусу ка­русели. Пробегая по вращающейся площадке, они стремятся спрыг­нуть внутрь карусели (к лестнице) в направлении близком к ее радиусу. Их следы на полу карусели дают их относительные пути bс, их проекции на пол под кару­селью — абсолютные пути bed. Дающие им направление перила на наклонной поверхности соответствуют направ­ляющим лопаткам. Перила на карусели, в которые люди должны при своем повороте упираться для своего пово­рота, соответствуют рабочим лопастям.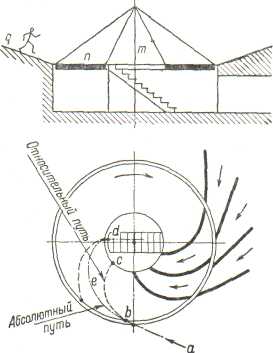


Рисунок 4.1 Карусель как модель работы сил реакции на вращающееся колесо.

4.1.2 Движение потока в направляющем аппарате.

Во всех реактивных турбинах поток, поступающий на рабочее колесо, формируется направляющим аппаратом, представляющим собой круговую решетку профилей (лопаток), что хорошо видно на рисунке 4.2.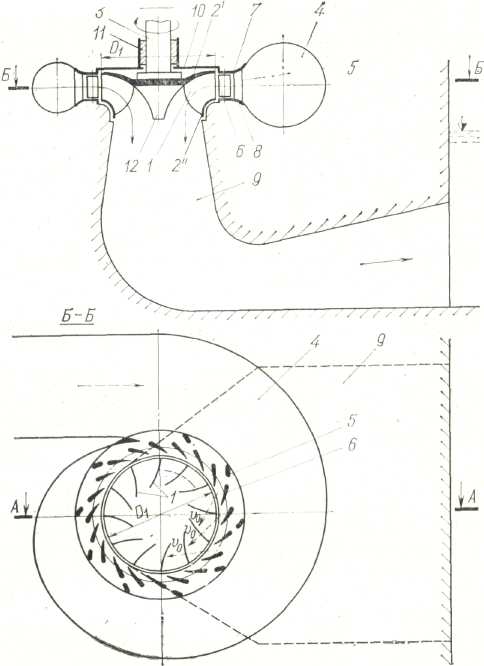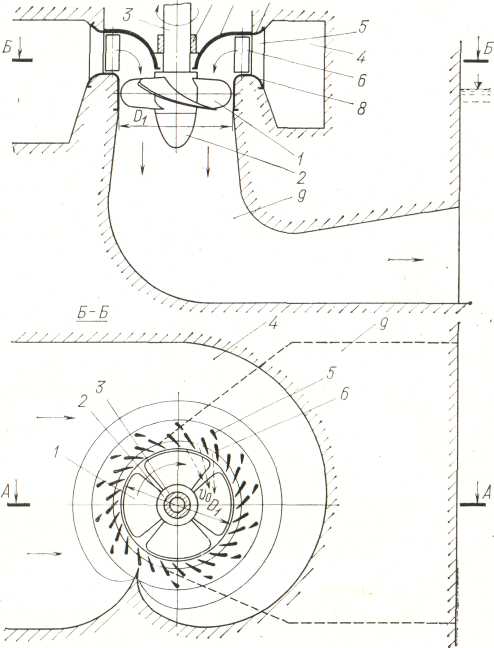



а) б)

Рисунок 4.2 Схемы турбин.

а– поворотно-лопастная; б – радиально-осевая.

Характерными показателями круговой решетки является форма профилей и густота решетки. Течение в пределах Н.А. является конфузорным* (конфузор (от лат. coniundo — вливаю, распределяю, смешиваю) — профилированный сужающийся канал, в котором дозвуковая скорость жидкости или газа возрастает в результате преобразования потенциальной энергии в кинетическую), а густая решетка лопаток обеспечивает практически полное совпадение направления потока на выходе, на диаметре D ₀₂, с направлением профиля выходных участков лопаток. Положение лопатки характеризуется величиной открытия а₀, которое определяет величину расхода и направление вектора V₀. Скорость потока (рисунок 4.3) в радиальном направляющем аппарате, направленная по касательной к выходному участку лопатки, вектор V₀ можно представить суммой двух слагаемых:

V₀ = V_{0 R} + V_{0 U}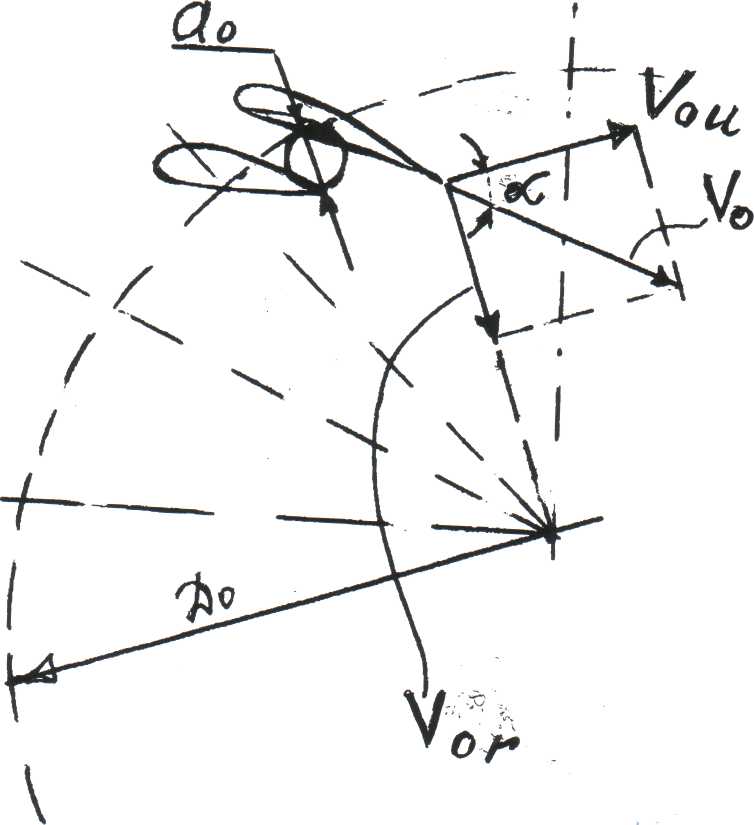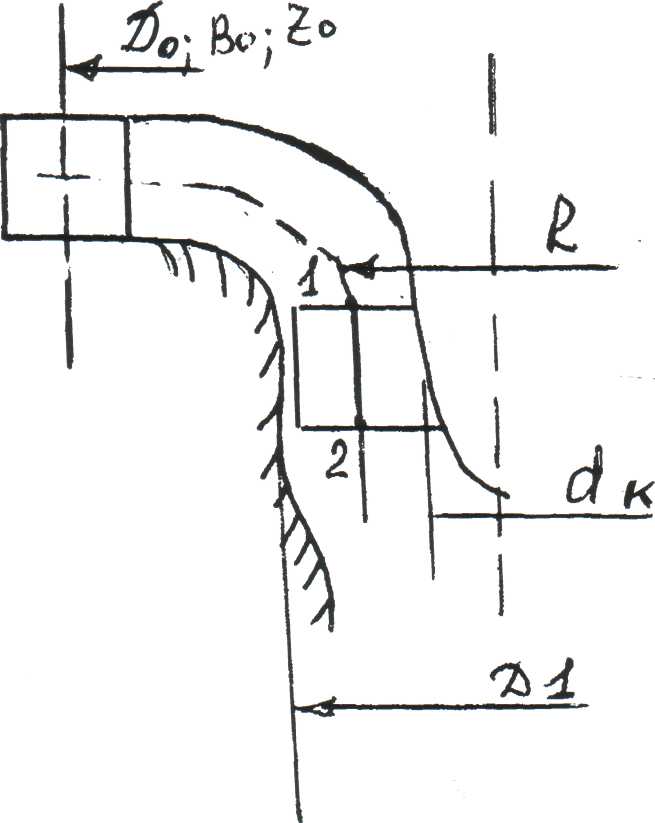

в которой V_{0 R}— радиальная составляющая; V_{0 U} — окружная составляющая.

Рисунок 4.3 Схема потока в направляющем аппарате.

Зная расход турбины Q=VSи размеры направляющего аппарата (D₀, b₀) радиальную компоненту определяем по формуле:

v_{0 R} = Q/πD₀b₀

Угол между V₀ и V_0U обозначим ά₀, тогда

v_o = v_0Rsinά₀ ,

а окружную составляющую определяем из соотношения

v_{o u} = v₀cosά₀.

Наличие окружной компоненты v_ou указывает на то, что поток за направляющим аппаратом «закручен» относительно оси в соответствии с профилем лопатки НА. Закрученность потока определяется величиной – циркуляция, обозначается Г, размерность м²/с.

Для осредненного потока за направляющим аппаратом, на его выходном диаметре D ₀₂ циркуляция равна:

Г₀ = π D₀₂v_ou = π D₀₂v₀cosά₀

Отсюда следует, что направляющий аппарат создает циркуляцию потока.

В пространстве (D ₀₂ – 1) на рисунке 4.3, между концами направляющих лопаток и входными кромками лопастей рабочего колеса («предколесное или предлопастное» пространство) жидкость движется свободно, а траектория струек потока задается геометрией проточной части.

Важно понять как при этом изменяется скорость потока. Выделим в потоке элементарную массу m на радиусе R. Используя закон механики о моменте количества движения: «Для выделенной массы, производная по времени от момента количества движения относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту массу относительно той же оси». Этот закон представляется формулой:

d(mv_ouR)_o /dt = ∑M_o ,

где: m – масса жидкости выделенного объема; v_ou окружная составляющая скорости; R – радиус; М_о – сумма моментов внешних сил, действующих на выделенную массу, относительно оси турбины О.

В итоге получим, что при свободном движении жидкости можно принять ∑М_О = 0, а это значит, что mv_ouR = const. Отсюда вытекает важная зависимость:

v_uR = const

Данное выражение определяет условия свободного движения жидкости в предлопастном пространстве и называется законом постоянства момента скорости.

С учетом того, что Г = 2π Rv_u, получим условие постоянства циркуляции при свободном движении жидкости:

Г = Г_О = const

Следовательно, в пространстве между направляющим аппаратом и рабочим колесом турбины циркуляция, созданная направляющим аппаратом сохраняется.

4.1.3 Кинематика потока в рабочем колесе реактивных гидротурбин.

Преобразование энергии жидкости в механическую энергию на валу осуществляется в рабочем колесе за счет взаимодействия потока с лопастями рабочего колеса, представляющего собой вра­щающуюся решетку профилей.

Гидродинамические свойства потока в рабочем колесе, ха­рактеризуемые пропускной способностью турбины – Q, скоростью вращения – n и к. п. д. – η, определяются величиной и направлением скоростей в потоке жидкости. Скорости потока в свою очередь зависят: от формы и размеров элементов проточной части турбины и рабочего напора Н.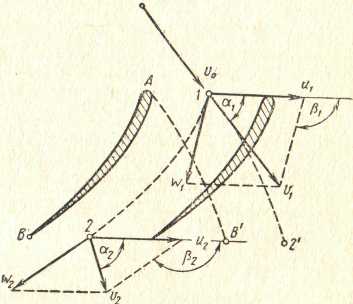

При исследовании движения жидкости в рабочем колесе это движение рассматривается как сложное, состоящее из двух движений: относительного и переносного. Относительное движение W жидкости фиксируется «наблюдателем», находящимся на рабочем колесе (движение ж., относительно системы координат прикрепленной к сосуду). Переносное движение Uопределяет движение самого рабочего колеса и его лопастей по отношению к неподвижным частям турбины.

В турбинах — это всегда вращение. Сумму

относительного и переносного движений называют абсолютным движением V, рисунок 4.4.

Рисунок 4.4 Скорости и траектория движения воды в межлопастном канале рабочего колеса РО турбины.

На рисунке 4.4 представлены следующие обозначения:

О — место ненарушенного (закрученного) потока непосредственно перед входом в каналы рабочего колеса, V_O – скорость потока в предлопастном пространстве, на входе в рабочее колесо;

1 — место непосредствен­но после входа в канал, на входной кромке лопастей ра­бочего колеса;

2 – место непосредственно перед выходом из канала на выходной кромке лопастей колеса;

Скорость переносного движения U. Скорость точек рабочего колеса при переносном движении(2 – 2') равнаокружной скорости, пропорциональной радиусам точек и угловой скорости:

v_U = ωr = 2πnr_i /60

Окружная скорость направ­лена по касательной к окружности данного радиуса r (нормальна к радиусам, лежащим в плоскостях нормальных к оси).

Скорость относительного движения W. Направление относительной скорости потока воды (1 – 2) определяется формой лопастей ра­бочего колеса и меняется по мере прохождения воды через рабочее колесо. Величина относительной скорости зависит от расхода воды проходящей через турбину.

v_W = Q/s =Q/πDb

Физический смысл V_W. Возьмем около лопастей в сечениях входа и выхода колеса точки 1 и 2. Отложим векторы относительных скоростей W₁ и W₂. Вода здесь течет вдоль стенок, почему и векторы должны быть здесь направлены вдоль элементов осей каналов, (т.е. по касательным к входной кромке лопасти W₁ и выходной кромки лопасти W₂).

Следовательно, если размер bканалов вдоль оси колеса (высота колеса) постоянен, то отно­сительные скорости и их векторы обратно про­порциональны ширине каналов (шагу решетки t = 2πr / z_лоп).

При этом, скорости угловая ω а следовательно, и окружные u предполагаются заданными.

Абсолютная скорость V. Складывая геомет­рически по правилу параллелограмма векторы скоростей относительных W и окружных U, получаем векторы абсолютных скоростей V.

V = W + U

Следовательно, векторы скоростей V, U и W образуют треугольник скоростей в соответствующей точке потока.

На рисунке 4.5 построены треугольники скоростей для точки входа 1 и точки выхода 2.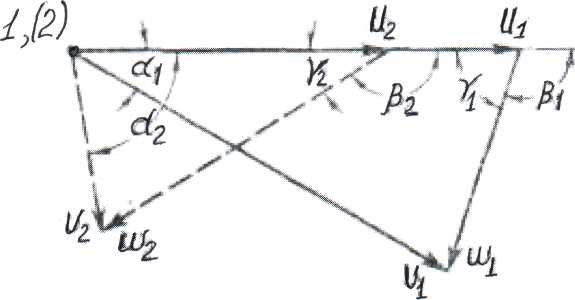


Рисунок 4.5 Треугольник скоростей для входа и выхода.
Определяя значения и направления скоростей, эти векторы определяют и углы между ними.

Углы между векторами абсолютных скоростей V и окружных U обычно обозначаются через ά (ά₁ — на входе и ά₂ — на выходе). Углы ά можно было бы называть углами абсолютной скорости или струйными, они зависят от работы турбины, в первую очередь от открытия направляющего аппарата.

Углы между векторами относительных скоростей W и окружных U через β (β₁ — на входе и β₂ — на выходе), дополнительные к ним через γ. Тогда γ = 180 – β. Углы β — углы отно­сительной скорости или лопастные, они зависят от кон­струкции и формы лопастей. У радиально-осевых и пропеллерных турбин эти углы остаются неизменными при всех режимах работы турбины.

Таким образом, при анализе течения жидкости в рабочем колесе в первом прибли­жении предполагают:

1. Рабочее колесо имеет большое число бесконечно тонких лопа­стей, вследствие чего путь воды в относительном движении будет иметь форму лопасти АВ или средней струйки 1—2 (рис. 4.4);

2. Все скорости считаются средними в рассматриваемом сечении,
нормальном к общему направлению потока;

3. При расчетном режиме работы турбины имеет место безударный вход воды на лопасти рабочего колеса.

Следует отметить: на рисунке 4.4 показаны траектории абсолютного движения: А-В'—для частицы, вышедшей из точки А и пришедшей в точку В', и 1-2' —для частицы жидкости, вышедшей из точки 1 и пришедшей в точку 2'.

Векторы абсолютных скоростей V₁ и V₂ касательны к этим траекториям в начале (1) и в конце пути (2').

Векторы относительных скоростей W₁ и W₂ касательны в на­чальных и конечных точках траекторий относительного движения А-В или 1-2.

4.1.3.1 Кинематика потока в рабочем колесе осевых реактивных гидротурбин.

У осевых турбин поверхности тока в рабочем колесе близки к цилиндрическим (рисунок 4.6, а), т. е. расчетный диаметр D_Р можно вычислить как средний по площади:

Д_Р =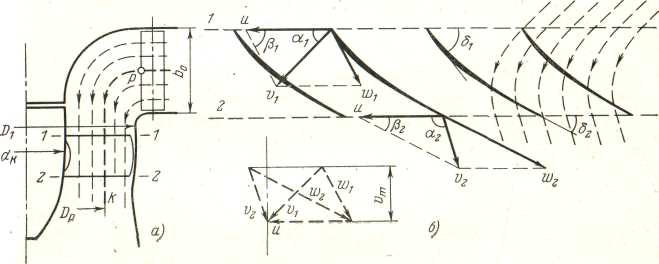



Рисунок 4.6. Поток в осевой турбине

Развертка цилиндрического сечения рабочего колеса показана на рисунке 4.6, б). Особенность состоит в том, что значение окружной скорости в точках 1 и 2 равны:

v_U = v _1U = v _2U = ωr = πD_Pn / 60

Меридианная составляющая абсолютной скорости v не изменяется от входа до выхода ( 1 – 2 ), тогда ее значение равно:

v_m = v_1m = v_2m =

Скорость на входных (1) и выходных (2) кромках опре­деляется как векторная сумма:

V₁ = V_1m + V_1u

Полученные в результате параллело­граммы скоростей показаны на рисунке 4.6, б). Треугольники скоростей на входной и выходной кромках совмещены (показаны пунктиром), поскольку они имеют одинаковые основание u и высоту v_m. Справа пунктирными линиями показаны траектории абсолютного движения жидкости в рабочем колесе.