шепель расчетка. "київський політехнічний інститут"
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
|
2.5. Першиий спосіб ділення. 2.5.1Теоритичне обґрунтування першого способу ділення: Нехай ділене Х і дільник Y є n-розрядними правильними дробами, поданими в прямому коді. В цьому випадку знакові й основні розряди операндів обробляються окремо. Знак результату визначається шляхом підсумовування по модулю 2 цифр, записаних в знакових розрядах. При реалізації ділення за першим методом здійснюється зсув вліво залишку при нерухомому дільнику. Черговий залишок формується в регістрі RG2 (у вихідному стані в цьому регістрі записаний Х). Виходи RG2 підключені до входів СМ безпосередньо, тобто ланцюги видачі коду з RG2 не потрібні. Час для підключення n+1 цифри частки визначається виразом t=(n+1)(tt+tc), де tt - тривалість виконання мікрооперації додавання-віднімання; tc - тривалість виконання мікрооперації зсуву. 2.5.2 Операційна схема: 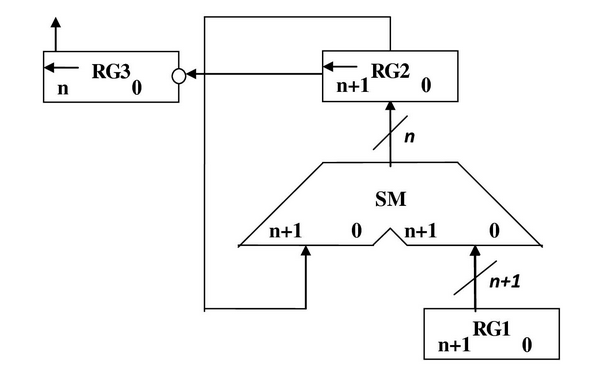 Рисунок 2.5.1- Операційна схема 2.5.3 Змістовний мікроалгоритм: Початок RG3:=0 RG2:=X RG1:=Y RG2[n+1] Кінець RG3:=l(RG3). RG2:=l(RG2).0 RG2:=RG2+RG1 RG2:=RG2+  +1 +1RG2[n+1] Рисунок 2.5.2-Змістовний мікроалгоритм 2.5.4 Таблиця станів регістрів:
2.5.5 Функціональна схема: 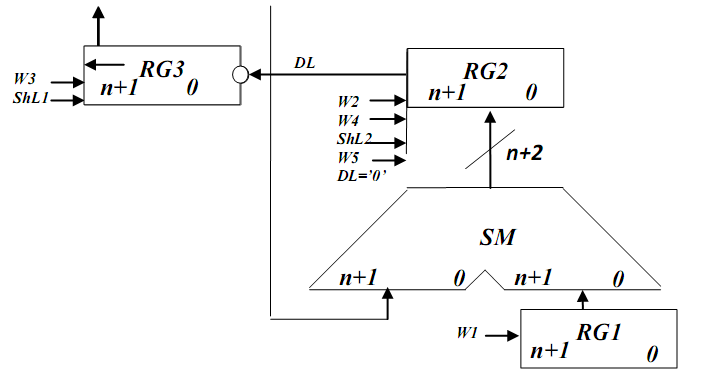 Рисунок 2.5.3 – Функціональна схема 2.5.6 Закодований мікроалгоритм Таблиця 2.5.2-Таблиця кодування операцій і логічних умов.
Z1 Початок Z2 W3, W2, W1 Z3 ShL1, ShL2 1 0 X1 Z5 Z4 W4 W5 1 X2 Z6 0 Кінець Рисунок 2.5.4-Закодований мікроалгоритм. 2.5.7 Граф управляючого автомата Мура з кодами вершин: 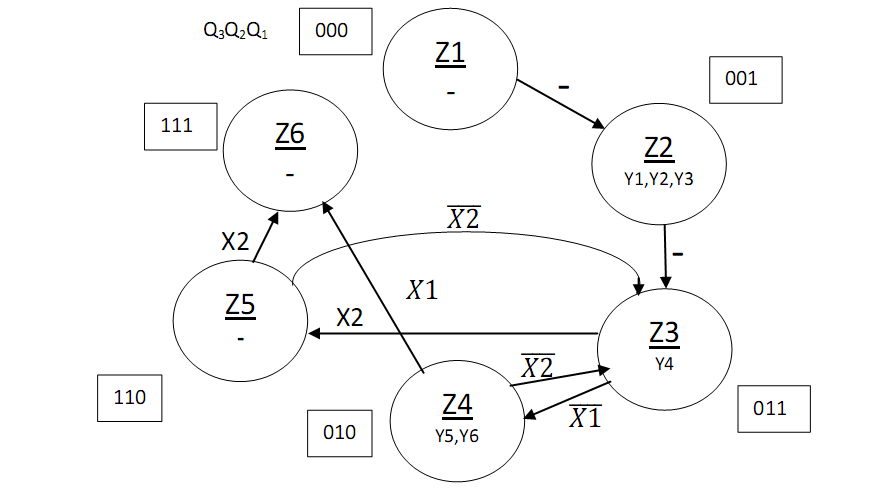 Рисунок 2.5.5 - Граф управляючого автомата. 2.5.8 Обробка порядків: Порядок частки буде дорівнювати: 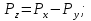 В моєму випадку 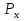 =8; =8; 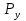 =5; =5; 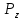 =3; =3;2.5.8 Нормалізація результату: Отримали результат: 1111010000001001 Знак мантиси: 1  0 = 1. 0 = 1.Нормалізація мантиси не потрібна.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
