шепель расчетка. "київський політехнічний інститут"
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
|
2.6. Другий спосіб ділення. 2.6.1Теоритичне обгрунтування другого способу ділення: Нехай ділене Х і дільник Y є n-розрядними правильними дробами, поданими в прямому коді. В цьому випадку знакові й основні розряди операндів обробляються окремо. Знак результату визначається шляхом підсумовування по модулю 2 цифр, записаних в знакових розрядах. Остача нерухома, дільник зсувається праворуч. Як і при множенні з нерухомою сумою часткових добутків можна водночас виконувати підсумування і віднімання, зсув в регістрах Y,Z. Тобто 1 цикл може складатися з 1 такту, це дає прискорення відносно 1-го способу. 2.6.2 Операційна схема 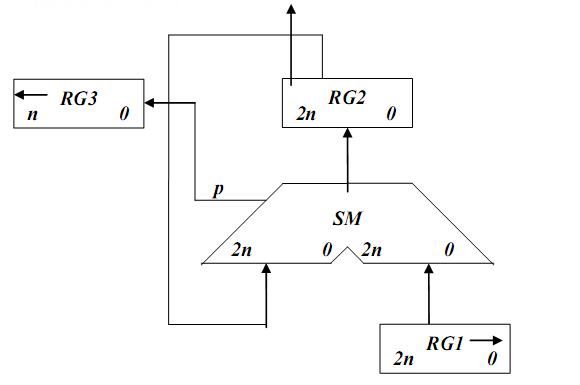 Рисунок 2.6.1-Операційнасхема 2.6.3 Змістовний мікроалгоритм Початок RG3:=0 RG1:=Y RG2=X RG2[2n+1] RG1:=0.r(RG1) RG3:=l.(RG3).SM(p) RG2:=RG2+RG1 RG1:=0.r(RG1) RG3:=l(RG3).SM(p) RG3[n] Кінець Рисунок 2.6.2-Змістовний мікроалгоритм 2.6.4 Таблиця станів регістрів Таблиця 2.6.1- Таблиця станіврегістрів
2.6.5 Функціональна схема з відображенням управляючих сигналів 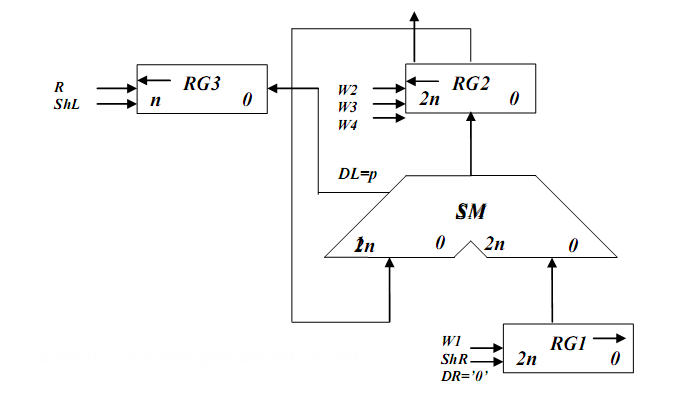 Рисунок2.6.3-Функціональна схема 2.6.6 Закодований мікроалгоритм Таблиця2.6.2- Таблиця кодуваннямікрооперацій
Початок R, W1, W2 X1 Кінець W4, ShR, ShL W3, ShR, ShL X2 Рисунок2.6.4- Закодованиймікроалгоритм 2.6.7 Граф управляючого автомата Мура з кодами вершин 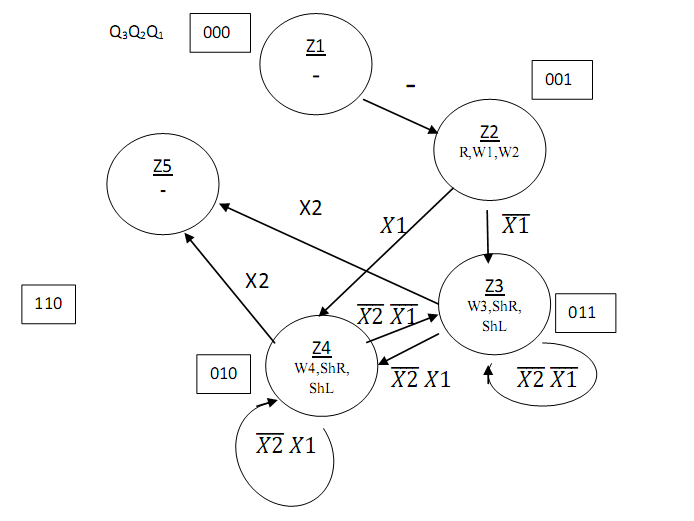 Рисунок2.6.5- ГрафавтоматаМура 2.6.8 Обробка порядків: Порядок частки буде дорівнювати: 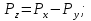 В моєму випадку 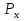 =8; =8; 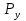 =5; =5; 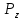 =3; =3;2.6.9 Нормалізація результату: Отримали результат: 1111010000001001 Знак мантиси: 1  0 = 1. 0 = 1.Нормалізація мантиси не потрібна.
2.7. Операція додавання чисел. 2.7.1 Теоретичне обґрунтування способу В пам’яті числа зберігаються у ПК. На першому етапі додавання чисел з плаваючою комою виконують вирівнювання порядків до числа із старшим порядком. На другому етапі виконують додавання мантис. Додавання мантис виконується у доповнювальних кодах, при необхідності числа у ДК переводяться в АЛП. Додавання виконується порозрядно на n-розрядному суматорі з переносом. Останній етап – нормалізація результату. Виконується за допомогою зсуву мантиси результату і коригування порядку результату. Порушення нормалізації можливо вліво і вправо, на 1 розряд вліво і на n розрядів вправо. 1. Порівняння порядків. Px=+810=+10002 Py=+510=+01012 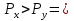 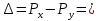 810-510=310=112 810-510=310=1122. Вирівнювання порядків. Робимо зсув вправо мантиси числа Y, зменшуючи  на кожному кроці, доки на кожному кроці, доки  не стане 0. не стане 0.Таблиця 2.7.1- Таблиця зсуву мантисинаетапівирівнюванняпорядків
3. Додавання мантис у модифікованому ДК. X мдк = 11. 101101110000111 Yмдк = 00. 000101101110000 Таблиця 2.7.2-Додавання мантис(для додавання)
Zпк = 1. 110011011110111 4. Нормалізація результату (В ПК). Для даного результату додавання нормалізація не потрібна. 2.7.2 Операційна схема  Рисунок2.7.1-Операційна схема Виконаємо синтез КС для визначення порушення нормалізації. Таблиця 2.7.4-Визначенняпорушеннянормалізації
Результат беремо по модулю, знак встановлюємо за Z’0 до нормалізації. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 +1
+1