шепель расчетка. "київський політехнічний інститут"
 Скачать 1.86 Mb. Скачать 1.86 Mb.
|
|
2.4 Четвертий спосіб множення. 2.4.1Теоритичне обґрунтування четвертого способу множення: Числа множаться у прямих кодах, знакові та основні розряди обробляються окремо. Визначення знака добутку здійснюють підсумування по модулю 2 цифр, що розміщуються в знакових розрядах співмножників. Множення здійснюється зі старших розрядів множника, сума часткових добутків залишається нерухомою, множене зсувається праворуч, множник ліворуч. 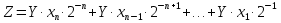 . .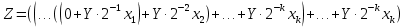 . .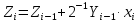 з початковими значеннями i=1, Y0=2-1Y, Z0=0. з початковими значеннями i=1, Y0=2-1Y, Z0=0.2.4.2 Операційна схема: 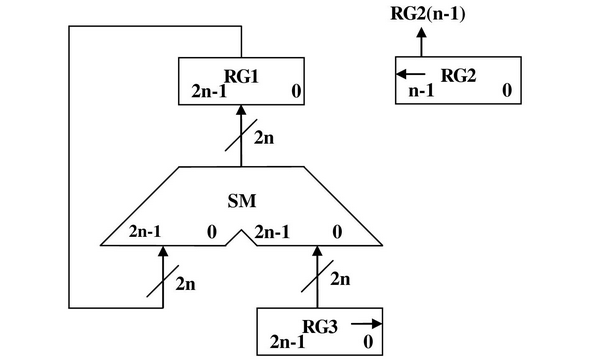 Рисунок 2.4.1- Операційна схема 2.4.3 Змістовний мікроалгоритм: RG1:=0; RG2:=X; RG3:=Y; RG3:=0.r(RG3) RG2[n-1] RG1:=RG1+RG3; RG3:=0.r(RG3) RG2:=l(RG2).0 RG2=0 Початок Кінець 1 1 0 0 Рисунок 2.4.2 - Змістовний мікроалгоритм. 2.4.4 Таблиця станів регістрів: Таблиця 2.4.1- Таблиця станіврегістрів
2.4.5Функціональна схема: 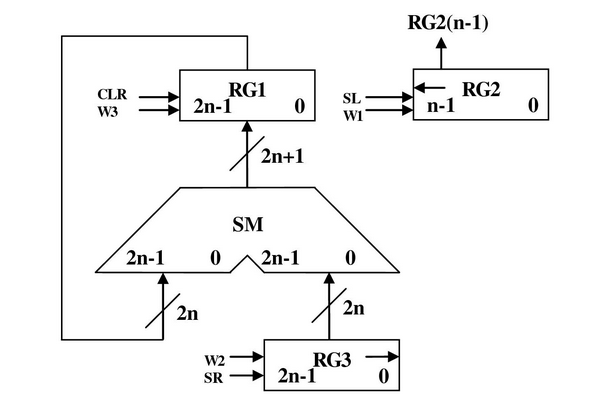 Рисунок 2.4.3 - Функціональна схема. 2.4.6 Закодований мікроалгоритм Таблиця 2.4.2-Таблиця кодування операцій і логічних умов.
Початок Z1 R, W2, W3, ShR X1 ShR,ShL X2 Кінець 1 0 1 0 Z2 Z3 Z4 Z5 W1 Рисунок 2.4.4-Закодований мікроалгоритм. 2.4.7 Граф управляючого автомата Мура з кодами вершин:  Рисунок 2.4.5 - Граф автомата Мура 2.4.8 Обробка порядків: Порядок добутку буде дорівнювати сумі порядків множників з урахуванням знаку порядків: 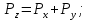 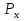 =8; =8; 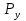 =5; =5; 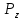 =1310=11012 =1310=110122.4.9 Нормалізація результату: Отримали результат: 100000101110010100000100110001 Знак мантиси: 1 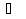 0 = 1. 0 = 1.Робимо здвиг результату вліво, доки у першому розряді не буде одиниця, Порядок понижаємо на 1: 100000101110010100000100110001; 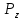 =12; =12;Запишемо нормалізований результат:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
