шепель расчетка. "київський політехнічний інститут"

Название	"київський політехнічний інститут"
Анкор	шепель расчетка.docx
Дата	12.08.2018
Размер	1.86 Mb.
Формат файла
Имя файла	шепель расчетка.docx
Тип	Документы #22847
страница	7 из 7

1 2 3 4 5 6 7

2.7.3 Змістовний алгоритм

Початок

CT:=m;

RGZ:=Z;

L=Z₀
Кінець

RGZ:=l(RGZ).0

RGPZ:=RGPZ-1

CT:=CT-1

RGZ:=RGZ(m+2).r(RGZ)

RGZP:=RGZP+1

R=

CT=0

1

Z’₀=0
Z’₀ Z₀:=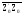

Рисунок2.7.2-Змістовний мікроалгоритм

2.7.4 Таблиця станів регістрів

1) Додавання

_Т_а_б_л_и_ц_я_2.₇_.₅_-_Т_а_б_л_иц_{я с}_т_а_н_і_в_р_е_г_і_с_т_р_і_в

№ такту	RGPZ	RGZ	ЛПН(L)	ППН(R)	СT	Мікрооперація
ПС	001000	11. 110011011110111 1110110010000100	0	1	100

2.7.5 Функціональна схема з відображенням керуючих сигналів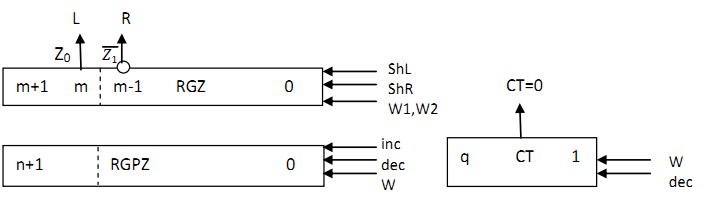

Рисунок 2.7.3 – Функціональна схема

2.7.6 Закодований мікроалгоритм

Таблиця 2.7.7– Таблиця кодування

1

Z6

Z2

Z3

Z4

Z5

Z1

1

Початок

W, W1

X2

Кінець

ShL, decRGZ, decCT

ShR, Inc

X3

X4

1

X1

W2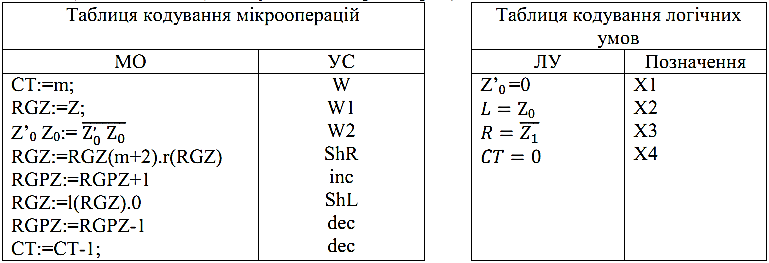

Рисунок 2.7.4 – Закодований мікроалгоритм

2.7.7 Граф управляючого автомата Мура з кодами вершин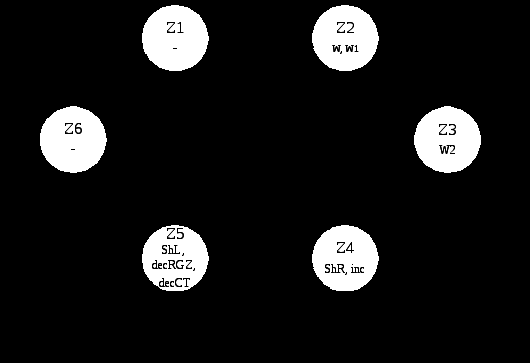

Рисунок 2.7.5 – Граф автомата Мура

2.7.8 Обробка порядків

P_X₊_Y= 8₁₀ =1000₂

2.7.9 Форма запису результату з плаваючою комою

Результат додавання Z=X+Y.

Z_пк = 1. 110011011110111

P_z = 8₁₀ =1000₂ M_z= 110011011110111₂

2.8.Операція добування кореня

2.8.1Теоритичне обґрунтування операції обчислення квадратного кореня

$c:\documents and settings\администратор\рабочий стол\безымянный14.bmp$

$c:\documents and settings\администратор\рабочий стол\безымянный15.bmp$

2.8.2 Операційна схема операції обчислення квадратного кореня 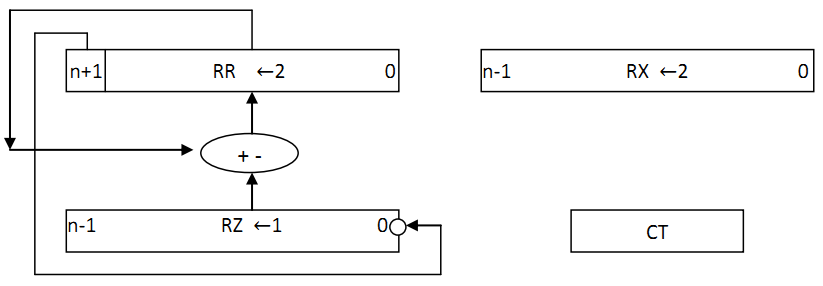$c:\documents and settings\администратор\рабочий стол\безымянный16.bmp$

Рисунок 2.8.1 –Операційна схем

2.8.3 Змістовний мікроалгоритм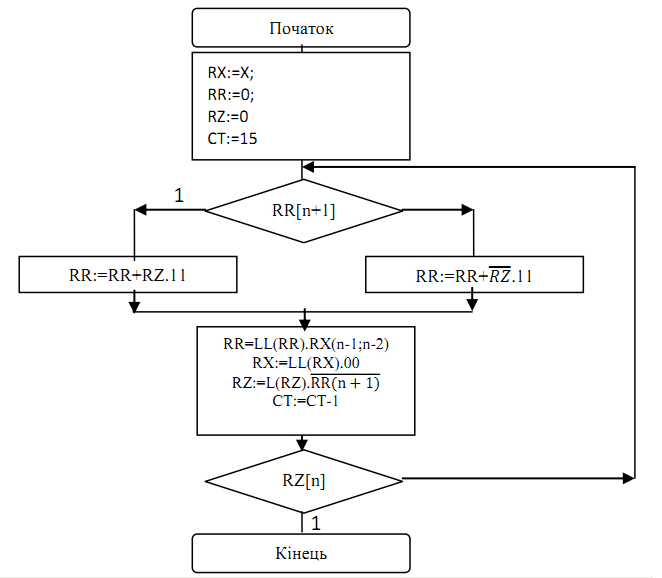

$c:\documents and settings\администратор\рабочий стол\безымянный17.bmp$

Рисунок 2.8.2 – Змістовний мікроалгоритм
2.8.4 Таблиця станів регістрів

Таблиця 2.8.1 – Таблиця станів регістрів

№	RZ	RR	RX	СТ
пс	000000000000000	00000000000000000 00000000000000010	010110111000011 001011011100001	1111
пз	000000000000000	00000000000000000 00000000000000010	010110111000011 001011011100001	1111
1	000000000000001	00000000000000010 + 11111111111111111 = 00000000000000001 00000000000000111	000101101110000	1110
2	000000000000011	00000000000000111 + 11111111111111011 = 00000000000000010 00000000000001001	000010110111000	1101
3	000000000000110	00000000000001001 + 11111111111110011 = 11111111111111100 11111111111110011	000001011011100	1100
4	000000000001101	11111111111110011 + 00000000000011011 = 00000000000001110 00000000000111000	000000101101110	1011
5	000000000011011	00000000000111000 + 11111111111001011 = 00000000000000011 00000000000001100	000000010110111	1010
6	000000000110110	00000000000001100 + 11111111110010011 = 11111111110011111 11111111001111111	000000001011011	1001
7	000000001101100	11111111001111111 + 00000000011011011 = 11111111101011010 11111110101101010	000000000101101	1000
8	000000011011000	11111110101101010 + 00000000110110011 = 11111111100011101 11111110001110100	000000000010110	0111
9	000000110110000	11111110001110100 + 00000001101100011 = 11111111111010111 11111111101011100	000000000001011	0110
10	000001101100001	11111111101011100 + 00000011011000011 = 00000011000011111 00001100001111100	000000000000101	0101
11	000011011000011	00001100001111100 + 11111001001111011 = 00000101011110111 00010101111011100	000000000000010	0100
12	000110110000111	00010101111011100 + 11110010011110011 = 00001000011001111 00100001100111100	000000000000001	0011
13	001101100001111	00100001100111100 + 11100100111100011 = 00000110100011111 00011010001111100	000000000000000	0010
14	011011000011110	00011010001111100 + 11001001111000011 = 11100100000111111 10010000011111100	010110111000011	0001
15	110110000111100	10010000011111100 + 01101100001111011 = 11111100101110111 11110010111011100	001011011100001	0000

2.8.5Функціональна схема операції обчислення квадратного кореня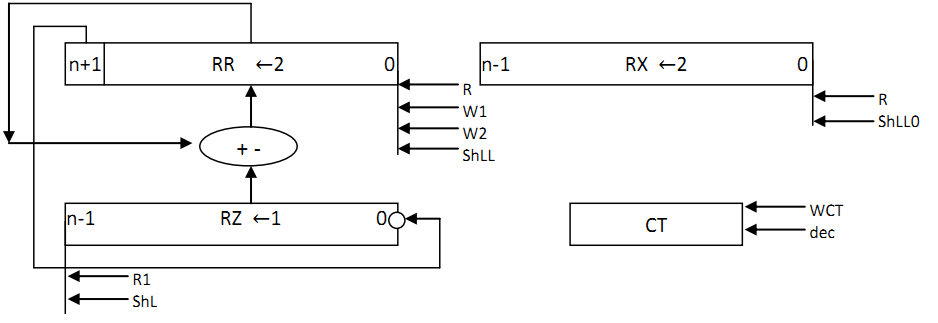

$c:\documents and settings\администратор\рабочий стол\безымянный18.bmp$

Рисунок 2.8.3 – Функціональна схема

2.8.6 Закодований мікроалгоритм

Таблиця 2.8.2 – Таблиця кодування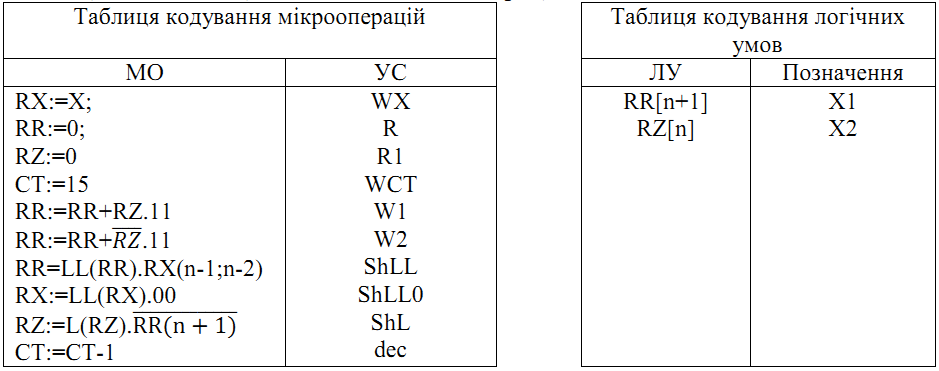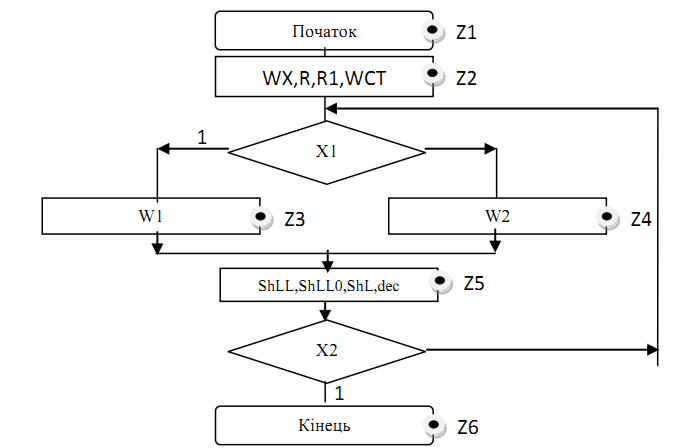

$c:\documents and settings\администратор\рабочий стол\безымянный19.bmp$

$c:\documents and settings\администратор\рабочий стол\безымянный20.bmp$

Рисунок 2.8.4 – Закодований мікроалгоритм

2.8.7Граф управляючого автомата Мура з кодами вершин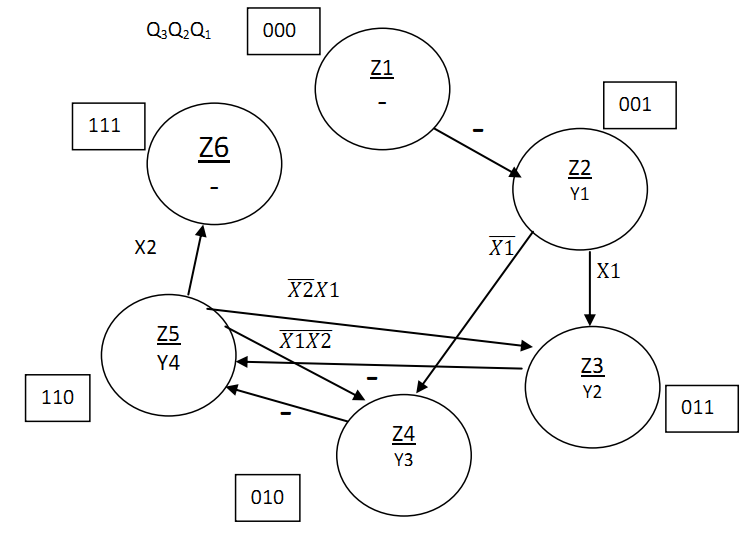

$c:\documents and settings\администратор\рабочий стол\безымянный21.bmp$

Рисунок 2.8.5 – Граф управляючого автомата Мура

2.8.8 Обробка порядків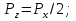

В моєму випадку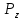

=4;

2.8.9 Запис результату

Отримали результат Z = 110110000111100;

Результат нормалізований, готовий до запису у мантису:

Завдання 3

x₃ x₂ x₁+1 = 100₂ = 4₁₀.

Синтез управляючого автомату Мура на D-тригерах для операції множення четвертим способом

3.1 Таблиця кодування сигналів

Таблиця 3.1 – Таблиця кодування сигналів

^R,^W²^,^W^3,^W_ст	Y1
W1	Y2
^S^hR,^S^hL^,^dec	Y3

3.2 Мікроалгоритм в термінах управляючого автомата Початок

Y1

X1
Y2

Y3

X2

Кінець

1

0

1

0

Z1

Z2

Z3

Z4

Z1

Рисунок 3.1 – Закодований мікроалгоритм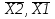

00

10

11

01

Z₁/-

Z₂/ Y1

Z₃/ Y2
Z₄/ Y3
-

X1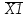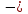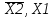

X2

3.3 Граф автомата

Рисунок 3.2 – Граф циклічного автомата

3.4 Таблиця переходів циклічного автомата на D-тригерах

Таблиця 3.2 – Таблиця переходів

Пер.		Ст. ст.	Нов. стан		Вх. сигн.		Вих. сигн.			Функції тригерів
		Q₂Q₁	Q₂Q₁		X₂X₁		Y₁Y₂Y₃			D₂		D₁
Z₁→Z₂	00			10		- -		0 0 0	1		0
Z₂→Z₃	10			11		- 1		1 0 0	1		1
Z₂→Z₄	10			01		- 0		1 0 0	0		1
Z₃→Z₄	11			01		- -		0 1 0	0		1
Z₄→Z₃	01			11		0 1		0 0 1	1		1
Z₄→Z₄	01			01		0 0		0 0 1	0		1
Z₄→Z₁	01			00		1 -		0 0 1	0		0

3.5 Мінімізація функцій тригерів

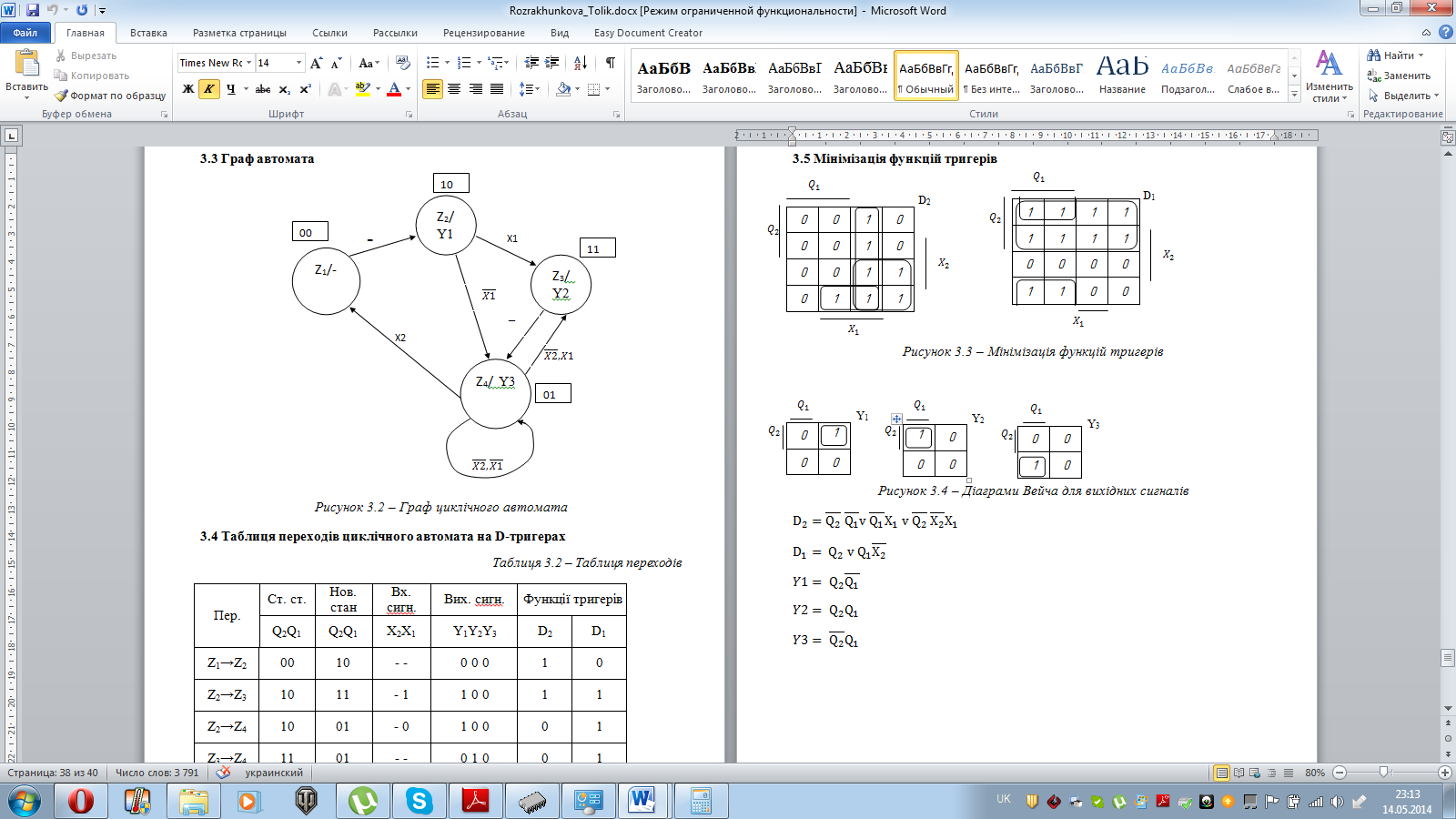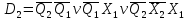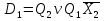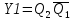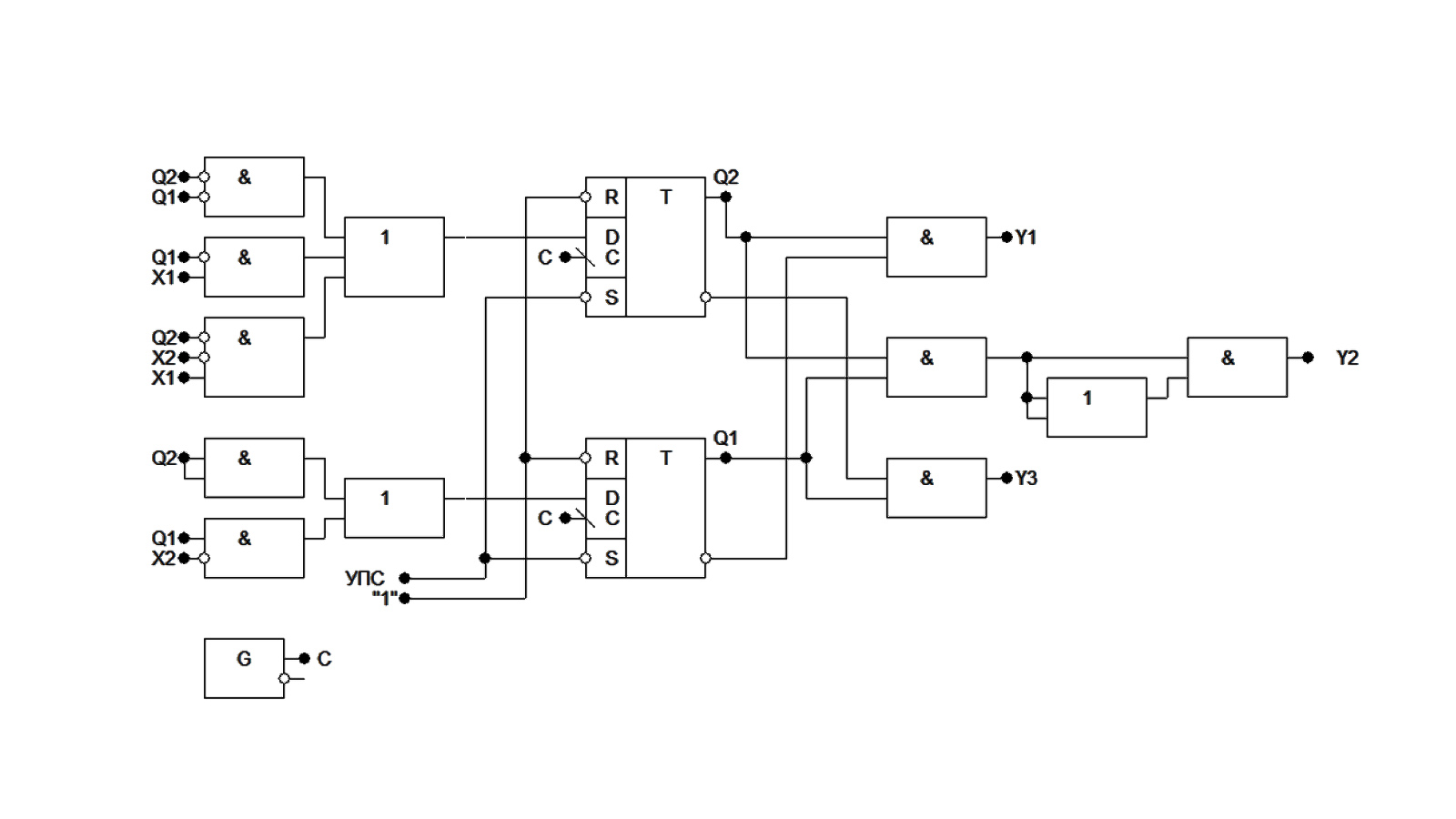$d:\1 курс\2-ий семестер\комп. арифметика\розрахункова\кс.jpg$

3.6 Функціональна схема автомата

Рисунок 3.5 - Функціональна схема в програмі AFDK

Висновок

У даній розрахунковій роботі було виконано операції з числами в двійковому коді з плаваючою комою, а саме: множення чотирма способами, ділення двома способами та додавання. Для операції множення другим способом було побудовано управляючий автомат Мура на D-тригерах і елементах булевого базису. Зроблено мінімізацію функцій тригерів і в середовищі AFDK побудована функціональна схема автомата.

Під час виконання даної розрахункової роботи я повторив для себе матеріал курсу «Компютерна логіка - 1», а також закріпив знання з курсу «Компютерна логіка - 2».

Було використано наступну літературу:

1) Жабін В.І., Жуков І.А., Клименко І.А.,Ткаченко В.В. Прикладна теорія цифрових автоматів: Навчальний посібник.–К.: Книжкове вид-во НАУ, 2009. – 360 с.

2) Конспект лекцій з курсу «Комп’ютерна логіка - 1»

3) Конспект лекцій з курсу «Комп’ютерна логіка - 2»

1 2 3 4 5 6 7