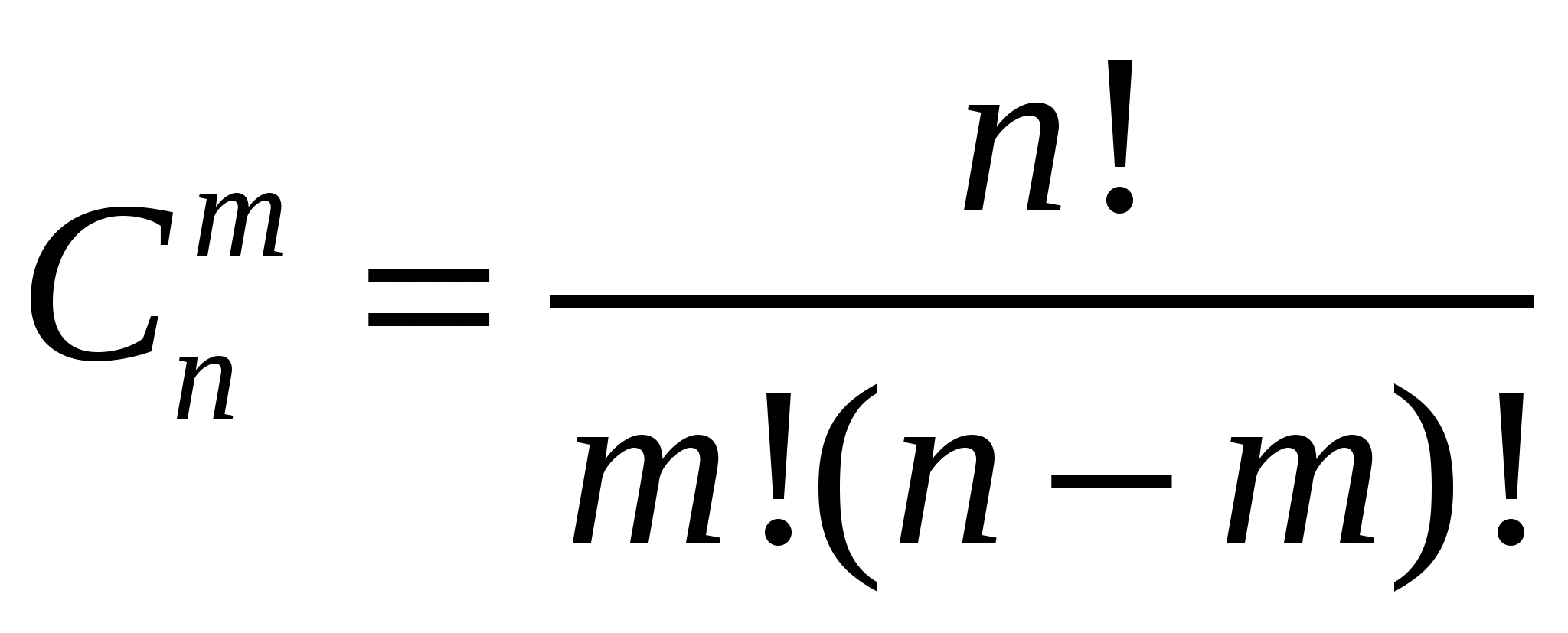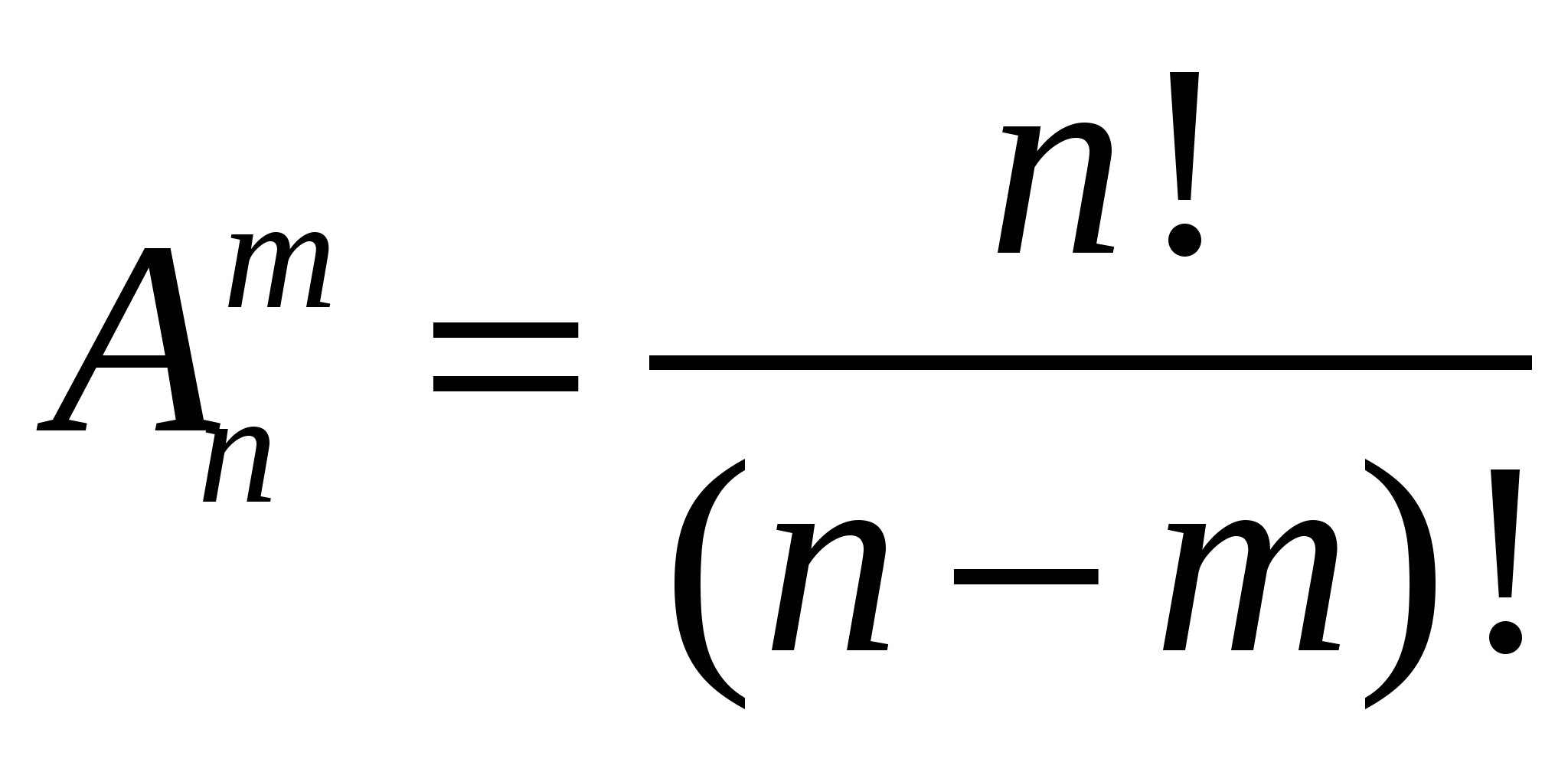Классическое определение вероятности события
В результате многократного повторения одних и тех же условий, которые носят название испытаний или опытов, можно наблюдать появление или непоявление в них некоторого события. Такое событие, которое может произойти или не произойти в результате опыта, называется случайным.
Во многих задачах рассматривается схема равновозможных событий. Например, при бросании игральной кости имеется одна и та же возможность появления любой из цифр от 1 до 6. Другим примером может служить выбор номера объекта при контрольной выборочной проверке.
Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом. Элементарный исход может быть рассмотрен либо как самостоятельное событие, либо как составляющая более сложного события.
На множестве всех элементарных исходов Q можно выделить подмножество, которое обладает заданными свойствами и определяет новое событие. Например, на множестве элементарных исходов при бросании игральной кости можно выделить подмножество таких исходов, которые соответствуют четному числу очков.
Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление такого события. В частности, появлению четного числа очков при бросании игральной кости соответствуют элементарные исходы с цифрами 2, 4, 6.
Количественной мерой возможности появления некоторого случайного события служит вероятность.
При классическом определении за вероятность события А принимается отношение числа благоприятствующих этому событию элементарных исходов (т) к общему числу возможных исходов (n):
Р(А) = m/ п
Для вычисления числа благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики.
Если составляются такие комбинации из п элементов по т, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из п элементов по т определяется по формуле
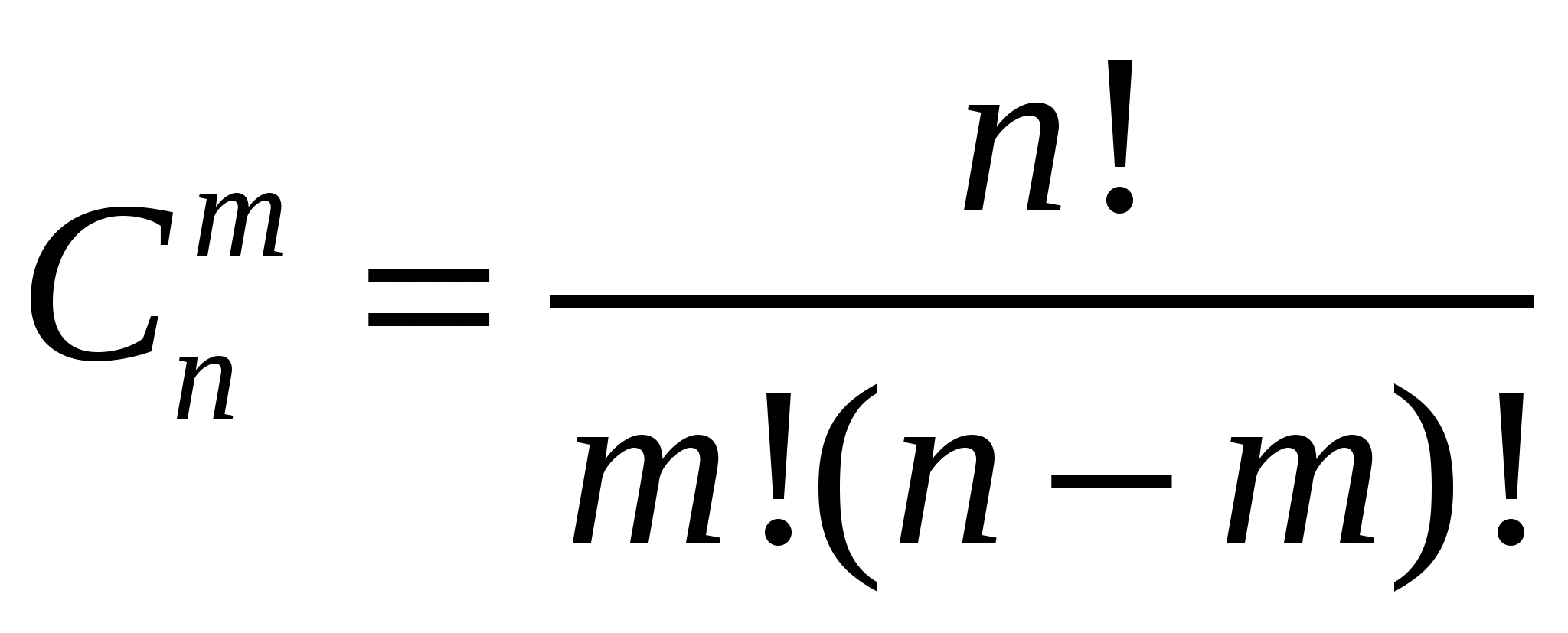
Если комбинации отличаются не только составом элементов, но и порядком их следования, то они называются размещениями. Их число находится цо формуле
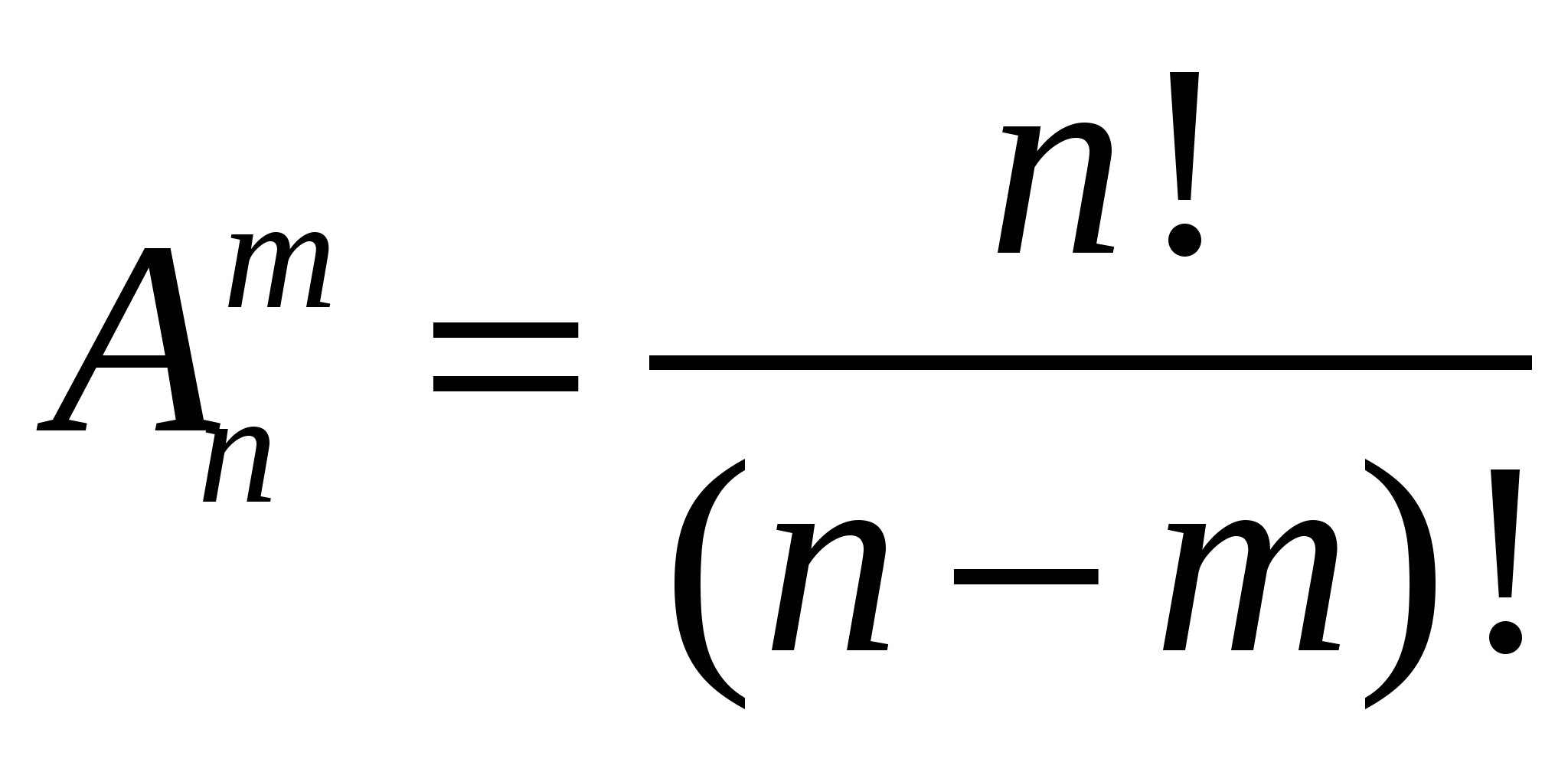
Если комбинации берутся из всех п элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно
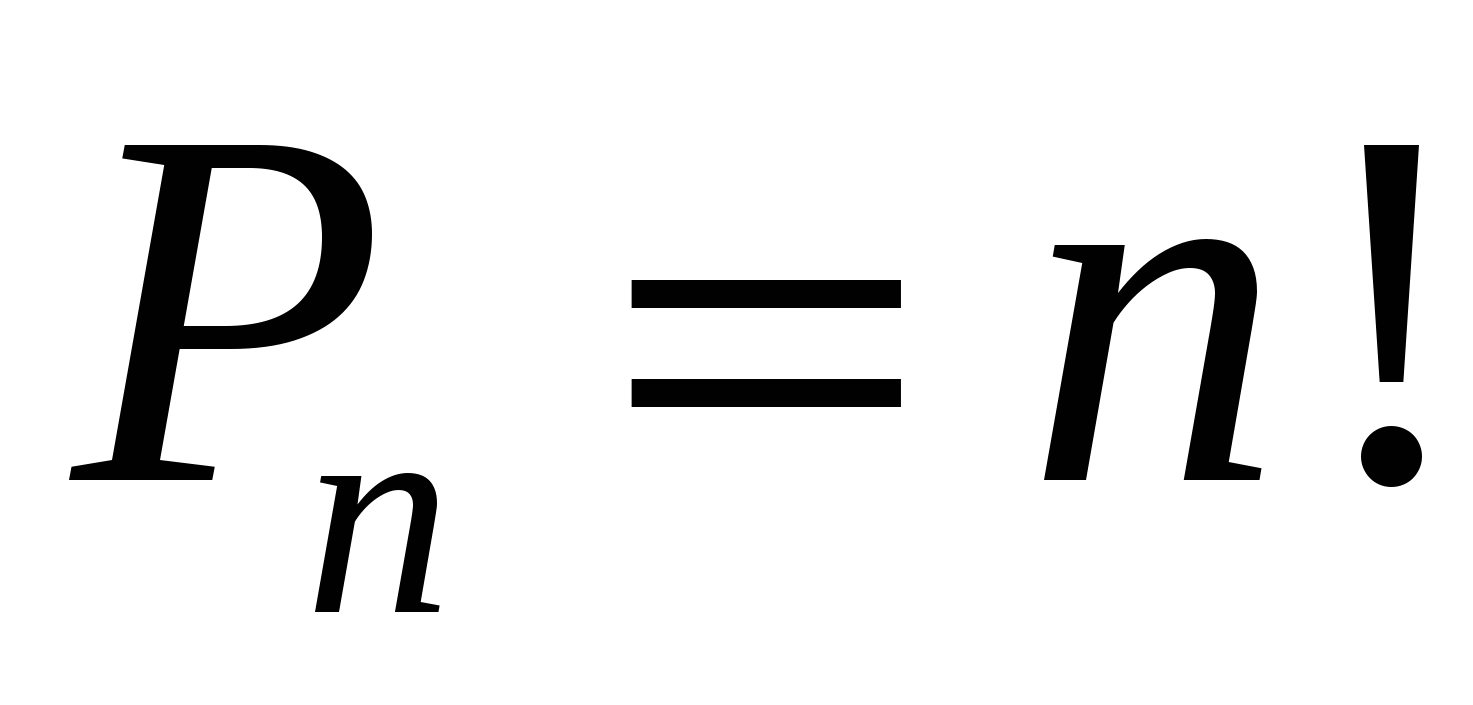
Задачи
В магазин постудило 30 холодильников, пять из них имеют заводской дефект. Случайным образом выбирается один холодильник. Какова вероятность того, что он будет без дефекта?
Игральную кость подбросили один раз. Какова вероятность того, что выпадет не менее пяти очков?
Пин код банковской карточки состоит из четырех цифр. Владелец карточки забыл последнюю цифру. Какова вероятность, не зная кода, набрать код правильно с первой попытки?
При игре в карты пользуются колодой из 36 карт. Какова вероятность того, что первой сданной картой будет не карта масти «пик»?
Выпущено 1000 лотерейных билетов. На 100 из них приходится выигрыш в 100 ден.ед., на 50 в 500 ден. ед. и на 10 в 1000 ден.ед. Студент приобрел один билет. Какова вероятность, что он
а) выиграет 1000 ден.ед.
б) не получит никакого выигрыша.
Выпущено 1000 лотерейных билетов. На 100 из них приходится выигрыш в 100 ден.ед., на 50 в 500 ден. ед. и на 10 в 1000 ден.ед. Студент приобрел два билета. Какова вероятность, что он
а) выиграет 2000 ден.ед.
б) выиграет 200 ден.ед.
в) выиграет 500 ден.ед.
б) не получит никакого выигрыша.
В классе учатся 10 юношей и 15 девушек. Для дежурства случайным образом отобраны три школьника. Найти вероятность того, что все дежурные окажутся юношами.
Какова вероятность, вытягивая из колоды в 36 карт 4 карты, вытянуть 2 дамы и два туза?
Комиссия по качеству раз в месяц проверяет качество продуктов в двух из 30 магазинов, среди которых находятся и два известных вам магазина. Какова вероятность того, что в течение месяца они оба будут проверены?
На станцию прибыли 10 вагонов разной продукции. Вагоны помечены номерами от одного до десяти. Найти вероятность того, что среди пяти выбранных для контрольного вскрытия вагонов окажутся вагоны с номерами 2 и 5?
Какова вероятность в игре «Спортлото 5 из 36» получить максимальный выигрыш (т.е. угадать 5 номеров)?
Изготовлена партия из 200 изделий, в которой оказалось три бракованных. Произведена выборка из пяти изделий. Найти вероятность следующих событий:
а) в выборке не будет ни одного бракованного изделия;
б) в выборке будет одно бракованное изделие?
В партии из 20 изделий 5 имеют скрытый дефект. Какова вероятность того, что из взятых наугад 10 изделий дефектными окажутся 2 изделия?
Из 20 акционерных обществ (АО) четыре являются банкротами. Гражданин приобрел по одной акции шести АО. Какова вероятность того, что среди купленных акций две окажутся акциями банкротов?
Из 100 изготовленных деталей 10 имеют дефект. Для проверки были отобраны пять деталей. Какова вероятность того, что среди отобранных деталей две окажутся бракованными? »
На склад привезли 50 ящиков комплектующих изделий для одного из видов ЭВМ, но среди них оказалось четыре ящика комплектующих для другого вида ЭВМ. Наудачу взяли шесть ящиков. Найти вероятность того, что в одном из этих шести ящиков окажутся некомплектные детали.
В партии из 15 однотипных стиральных машин пять машин изготовлены на заводе А, а 10 — на заводе В. Случайным образом отобрано 5 машин. Найти вероятность того, что две из них изготовлены на заводе А.
В коробке находится шесть одинаковых по форме и близких по диаметру сверл. Случайным образом сверла извлекаются из коробки. Какова вероятность того, что сверла извлекутся в порядке возрастания их диаметра?
На трех карточках помещены буквы «Г», «О», «Д». Карточки перемешаны и случайным образом подкладываются одна к другой. Какова вероятность, что получится слово «ГОД».
На пяти карточках напечатана одна из следующих букв: п,о,р,т,с. Вынимая последовательно из ящика карточки наугад и выкладывая их в одну линию, можно получить слово «СПОРТ». Какова вероятность этого события?
На шести карточках написаны буквы А, В, К, М, О, С. После перемешивания вынимают наугад одну карточку за другой и раскладывают по порядку. Найти вероятность того, что при этом получится слово «МОСКВА».
Дано 5 карточек с буквами К, М, Р, О, Я. Найти вероятность того, что:
а) наугад выбранные и разложенные в ряд одна за другой три карточки образуют слово РОМ;
б) при случайном расположении в ряд всех пяти карточек получится слово МОРЯК.
Некто забыл последние две цифры телефонного номера, но помнит, что они нечетные и различные. Какова вероятность того, что он сразу наберет нужный номер, если будет набирать эти цифры случайно?
Пин код банковской карточки состоит из четырех цифр. Некто забыл пин код, но помнит, что все цифры разные. Какова вероятность, не зная кода, набрать код правильно с первой попытки?
Пин код банковской карточки состоит из четырех цифр. Некто забыл пин код, но помнит, что все цифры одинаковые. Какова вероятность, не зная кода, набрать код правильно с первой попытки?
Пин код банковской карточки состоит из четырех цифр. Некто забыл пин код, но помнит, что код содержит три одинаковые цифры. Какова вероятность, не зная кода, набрать код правильно с первой попытки?
Пин код банковской карточки состоит из четырех цифр. Некто забыл пин код, но помнит, что код содержит две пары одинаковых цифр. Какова вероятность, не зная кода, набрать код правильно с первой попытки?
Брошены два кубика. Найти вероятность того, что сумма выпавших очков будет не менее 10.
Игрок бросает два кубика. Если выпадает равное число очков, он получает выигыш. Какова вероятность получить выигрыш? Решить эту же задачу для трех кубиков.
На первом этаже в лифт вошло 7 человек. В доме 10 этажей. Найти вероятности событий:
А) все выйдут на разных этажах
Б) все выйдут на одном этаже
В) все выйдут на последнем этаже
Теоремы сложения и умножения вероятностей
События называются несовместными, если они не могут появиться вместе в одном опыте.
Если одно из событий произойдет обязательно, то такие события образуют полную группу.
Суммой событий называется событие, состоящее в появлении хотя бы одного из рассматриваемых событий.
Теорема сложения вероятностей несовместных событий. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
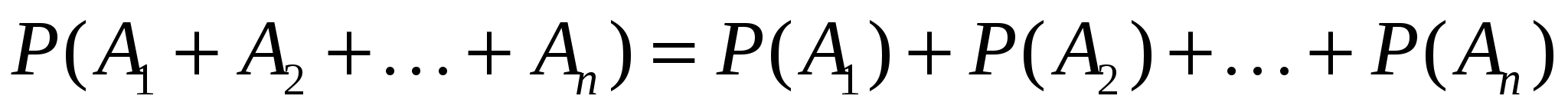
Сумма вероятностей событий, образующих полную группу, равна единице.
Произведением событий называется событие, состоящее в появлении всех из рассматриваемых событий.
Вероятность события В, вычисленная при условии, что произошло событие А, называется условной вероятностью события В относительно события А. Эта вероятность обозначается Р(В/А).
Теорема умножения вероятностей двух событий. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность второго относительно первого:
Р{АВ) = Р(А)Р(В/А) = Р(В)Р(А/В).
Если появление одного из событий не влияет на вероятность появления другого, то такие события называются независимыми.
Для независимых событий вероятность их произведения равна произведению вероятностей этих событий. Для двух независимых событий
Р(АВ) = Р(А)Р(В).
События называются совместными, если они могут появиться одновременно в одном опыте.
Теорема сложения вероятностей двух совместных событий. Веро-ятность сложения двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления-.
Р(А + В)= Р(А) + Р(В) - Р(АВ).
Задачи
Вероятности событий A и B равны соответственно 0,3 и 0,4. Чему равна вероятность их суммы, если вероятность их произведения 0,1?
На полке находится 10 книг, расставленных в произвольном порядке. Из них три книги по теории вероятностей, три — по математическому анализу и четыре — по линейной алгебре. Студент случайным образом достает одну книгу. Какова вероятность того, что он возьмет книгу по теории вероятностей или по линейной алгебре?
Магазин получил продукцию в ящиках с четырех оптовых складов: четыре с первого, пять со второго, семь с третьего и четыре с четвертого. Случайным образом выбран ящик для продажи. Какова вероятность того, что это будет ящик с первого или с третьего склада?
Вероятности попадания в цель при стрельбе из трех орудий равны соответственно 0,7, 0,8 и 0,5. Какова вероятность того, что первое и второе орудия промахнулись?
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что
А) потребитель увидит обе рекламы
Б) потребитель увидит только рекламу в каталоге
В) потребитель не увидит рекламы этого товара
Прибор выходит из строя, если выходит из строя любой из трех его узлов, работающих независимо. Вероятности выхода из строя в течение года соответственно узлов равны 0,3; 0,2; 0,25. Найти вероятность того, что прибор в течение года не выйдет из строя.
На полке стоят одинаковые по внешнему виду книги: 2 по математике и 3 по физике. Студент последовательно просматривает книги до тех пор, пока не найдет книгу по математике. Какова вероятность того, что ему придется просмотреть 4 книги?
Охотник может произвести по летящей дичи один за другим три выстрела с вероятностями попадания соответственно 0,8; 0,6 и 0,4. Стрельба прекращается после попадания в цель. Найти вероятность того, что охотник: а) попадет в дичь при третьем выстреле; б) произведет все три выстрела.
Первый стрелок попадает в цель с вероятностью 0,6, а второй с вероятностью 0,8. Каждый стрелок сделал по одному выстрелу. Какова вероятность того, что один из них промахнулся?
В порт приходят корабли только из трех пунктов отправления. Вероятность появления корабля из первого пункта равна 0,2, из второго пункта — 0,6. Найти вероятность прибытия корабля из третьего пункта.
Контролер проверяет изделия на соответствие стандарту. Известно, что вероятность соответствия стандарту изделий равна 0,9.
а) Какова вероятность того, что из двух проверенных изделий оба будут стандартными, если события появления стандартных изделий независимы?
б) Какова вероятность того, что из двух проверенных изделий только одно стандартное?
Вероятность правильного оформления счета на предприятии составляет 0,95. Во время аудиторской проверки были взяты два счета. Какова вероятность того, что только один из них оформлен правильно?
Вероятность правильного оформления накладной при передаче продукции равна 0,8. Найти вероятность того, что из трех накладных только две оформлены правильно.
Среди 20 электролампочек 3 нестандартные. Одновременно берут 3 лампочки. Найти вероятность того, что не менее двух лампочек будут стандартными.
При въезде в новую квартиру в осветительную сеть было включено 4 новые электролампочки. Каждая электролампочка в течение года может перегореть с вероятностью 0,8. Найти вероятность того, что в течение года из числа включенных в начале года придется заменить новыми: а) не менее 3 ламп; б) не более 3 ламп.
В районе 100 поселков. В пяти из них находятся пункты проката сельхозтехники. Случайным образом отобраны два поселка. Какова вероятность того, что в них окажутся пункты проката?
В городе находятся 15 продовольственных и 5 непродовольственных магазинов. Случайным образом для приватизации были отобраны три магазина. Найти вероятность того, что все эти магазины непродовольственные.
В магазине имеются 10 женских и б мужских шуб. Для анализа качества отобрали три шубы случайным образом. Определить вероятность того, что среди отобранных шуб окажутся:
а) только женские шубы;
б) только мужские или только женские шубы.
На предприятие поступают заявки от нескольких торговых пунктов. Вероятности поступления заявок от пунктов А и В равны соответственно 0,5 и 0,4. Найти вероятность поступления заявок от пункта А или от пункта В, считая события поступления заявок от этих пунктов независимыми, но совместными.
В вазе стоят 3 розы и 7 гвоздик. Выбирается случайным образом 3 цветка. Найти вероятность того, что выбранными окажутся: а) все розы; б) не менее 2 гвоздик.
Студент разыскивает нужную ему формулу в трёх учебниках. Вероятность того, что формула содержится в первом учебнике 0,4, во втором – 0,7, в третьем – 0,6. Найти вероятность того, что:
а) формула содержится во всех учебнике;
б) формула содержится только в двух учебниках;
г) формулы нет ни в одном из учебников.
д) формула содержится хотя бы в одном учебнике;
Покупатель может приобрести акции трех компаний: А, В и С. В течение следующего года надежность первой компании оценивается экспертами в 99%, второй – в 98%, третьей - 97%. Чему равна вероятность того, что
а) все три компании станут банкротами?
Б) ни одна компания не обонкротится
В) обанкротится только компания А
Г) обанкротятся компания А и компания С
в) только одна компания в течение следующего года станет банкротом
г) две компании обанкротятся
Вероятность появления хотя бы одного события
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb.