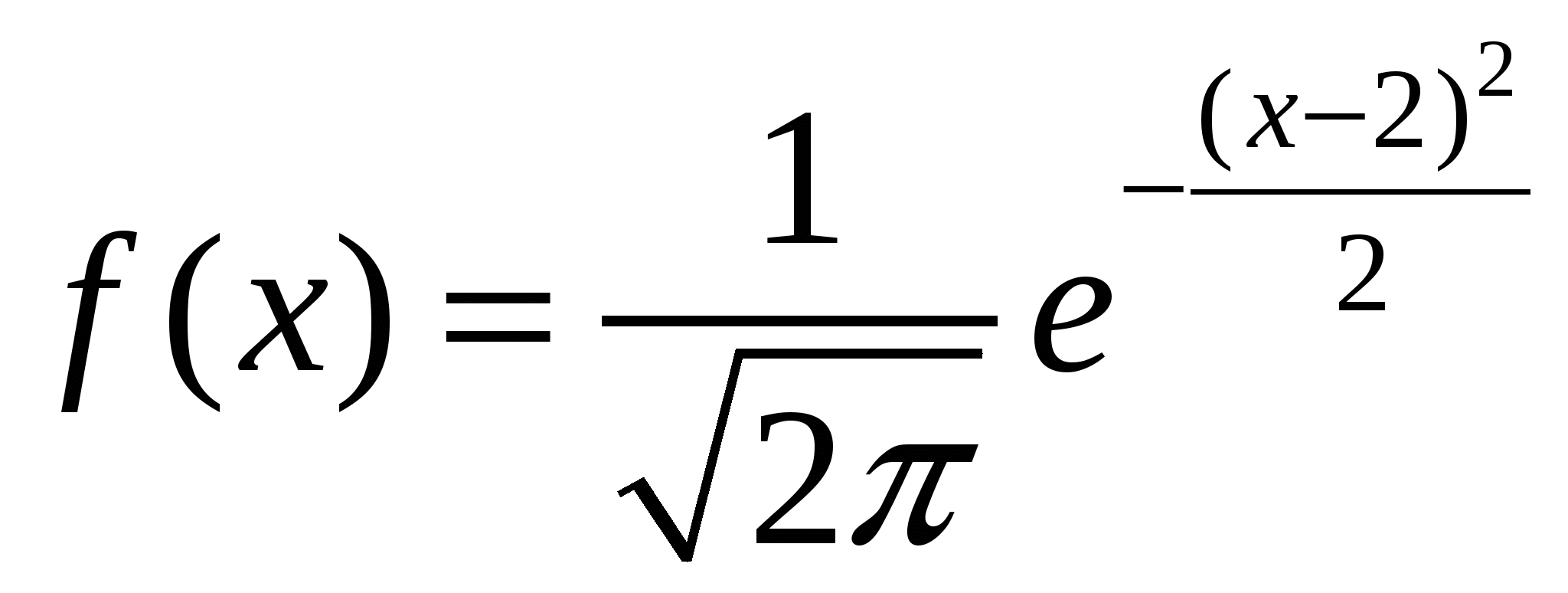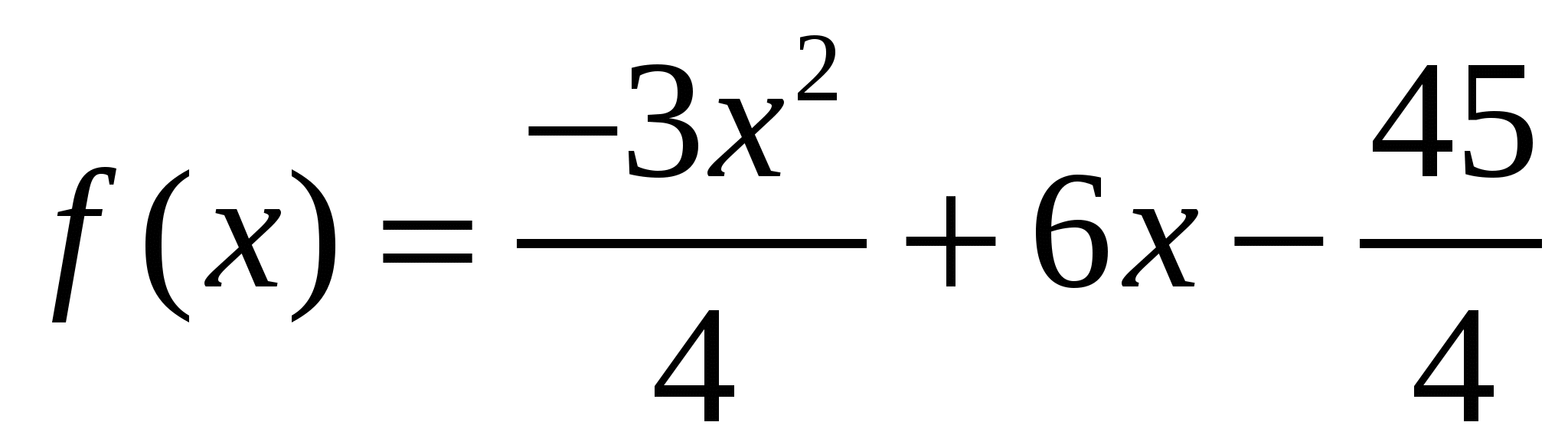Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.
Вероятность события 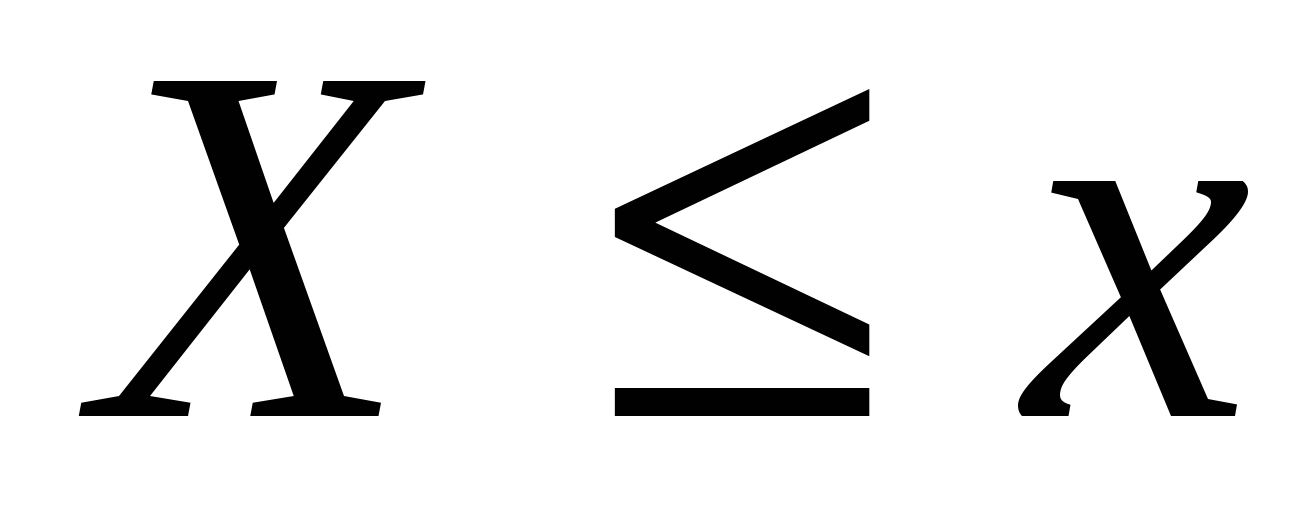 (где X — значение непрерывной случайной величины, а х — произвольно задаваемое значение), рассматриваемая как функция от х, называется функцией распределения вероятностей: (где X — значение непрерывной случайной величины, а х — произвольно задаваемое значение), рассматриваемая как функция от х, называется функцией распределения вероятностей:
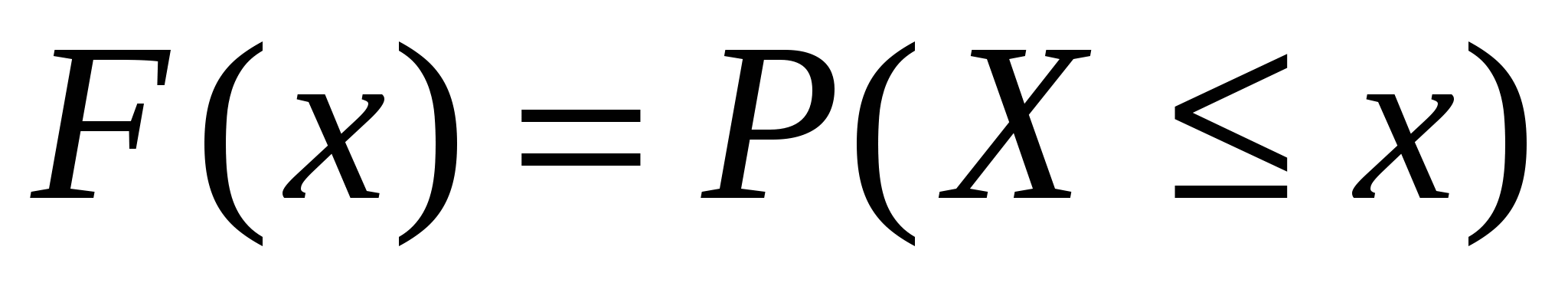 . .
Производная от функции распределения вероятностей называется плотностью распределения вероятности
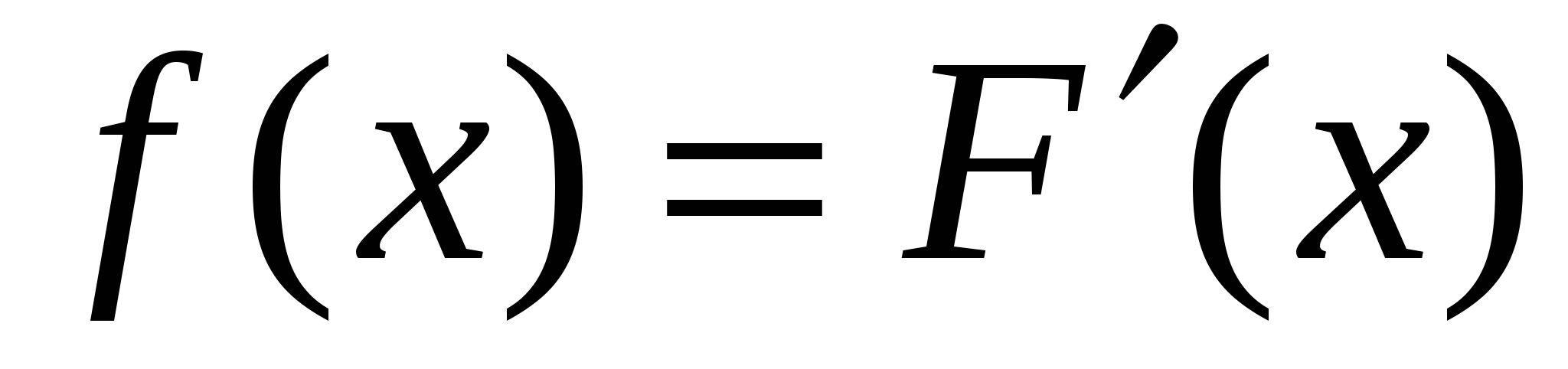 . .
Функция распределения вероятностей выражается через плотность в виде интеграла:
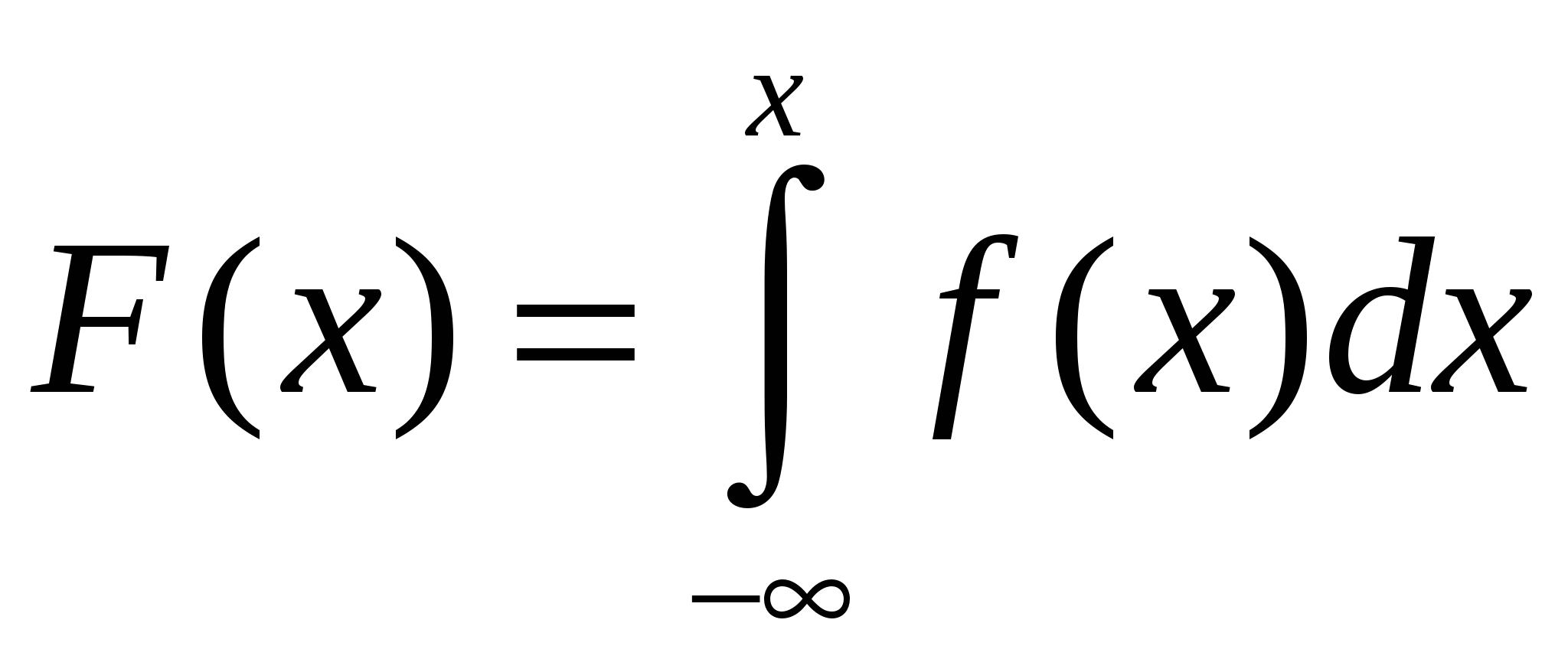
Вероятность попадания случайной величины в интервал [x1 х2] равна
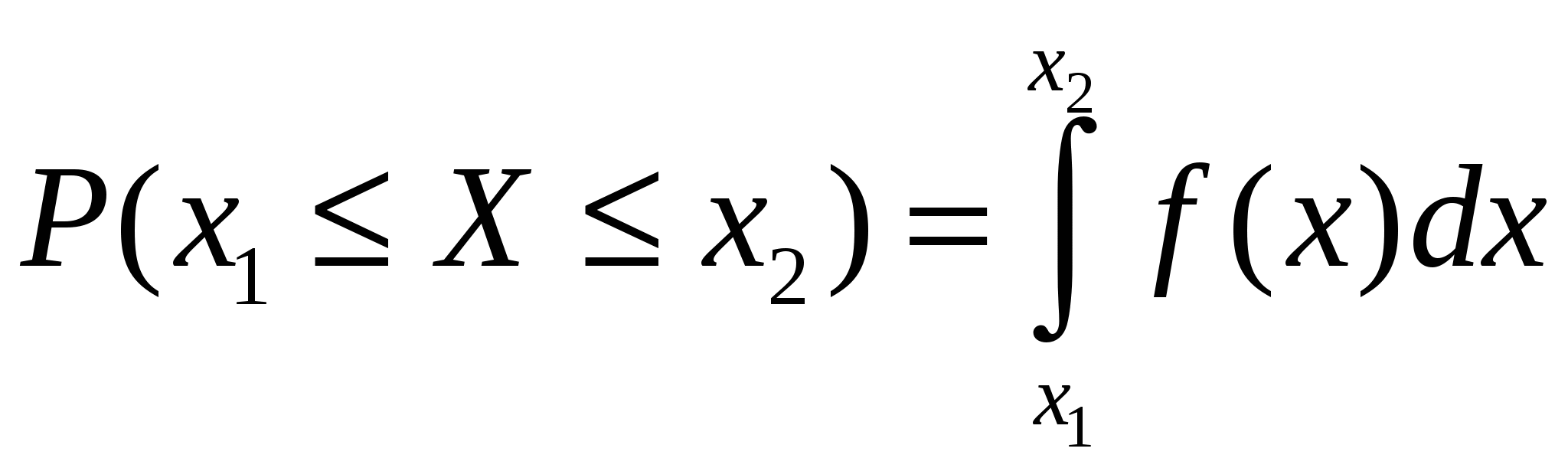 или или
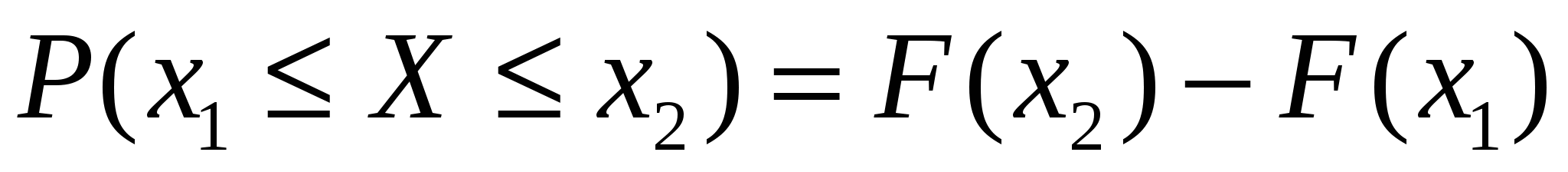
Случайная величина X задана функцией распределения вероятностей
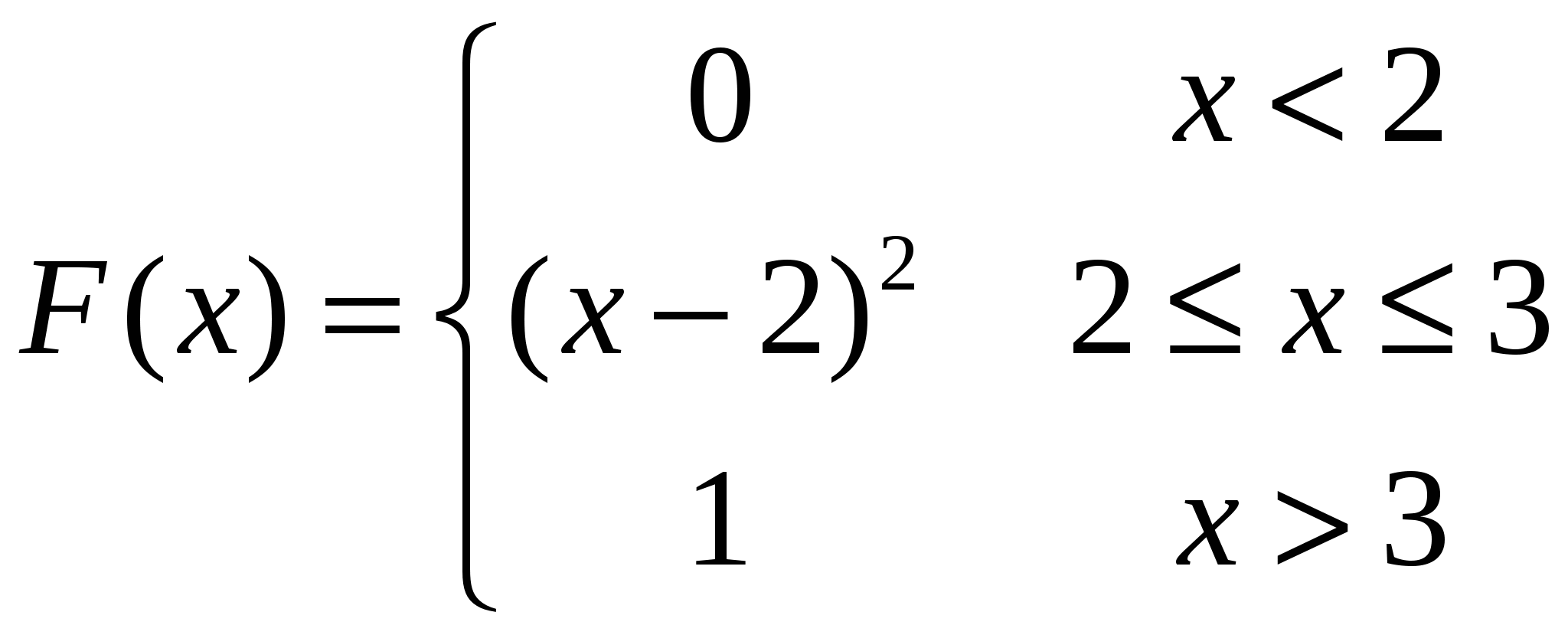
Найти плотность вероятности f(x) и вероятность попадания случайной величины в интервалы [1;2,5], (2,5;3,5).
Плотность вероятности непрерывной случайной величины X
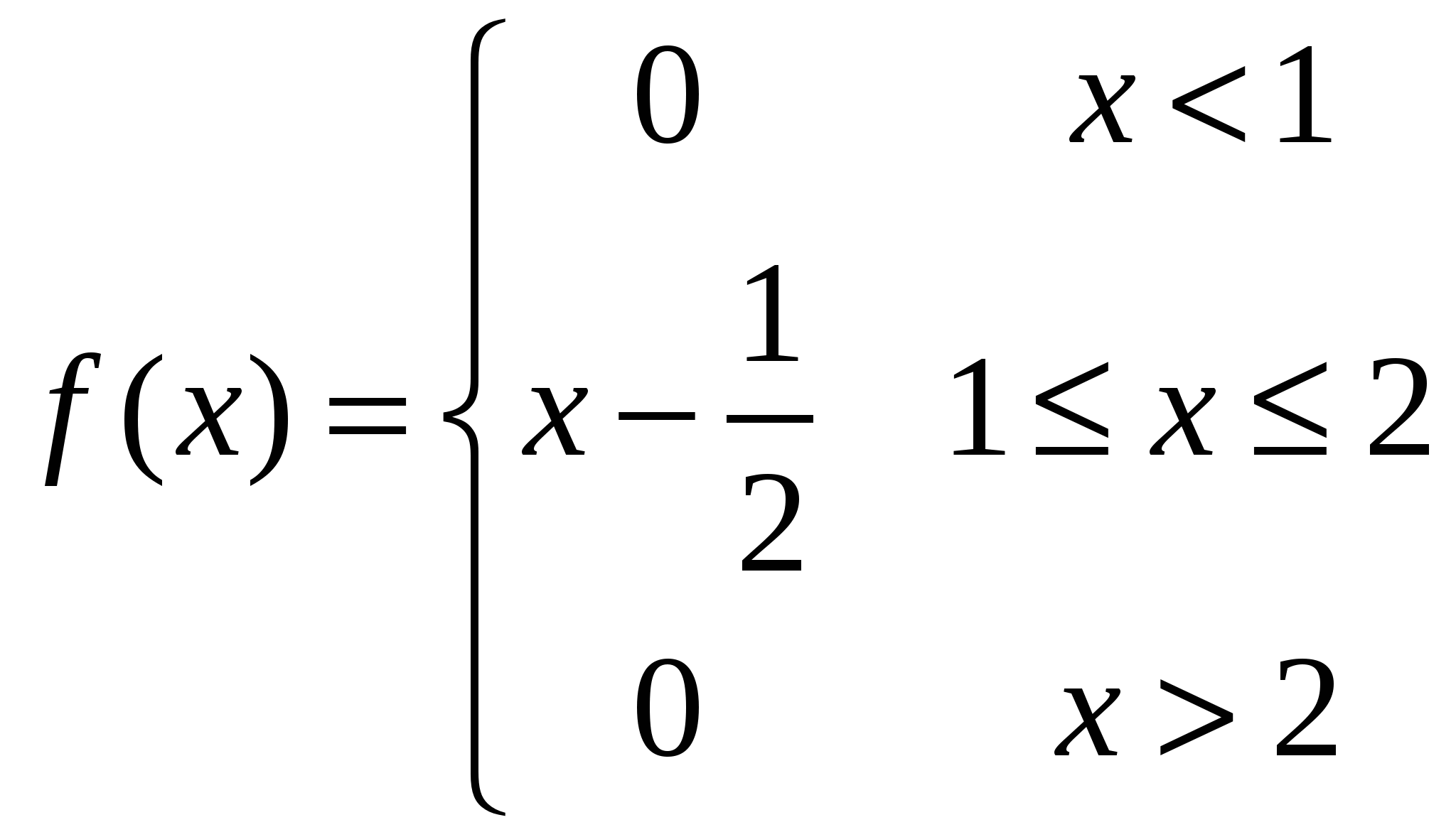
Найти функцию распределения F(x) и построить ее график.
Случайная величина X имеет плотность вероятности
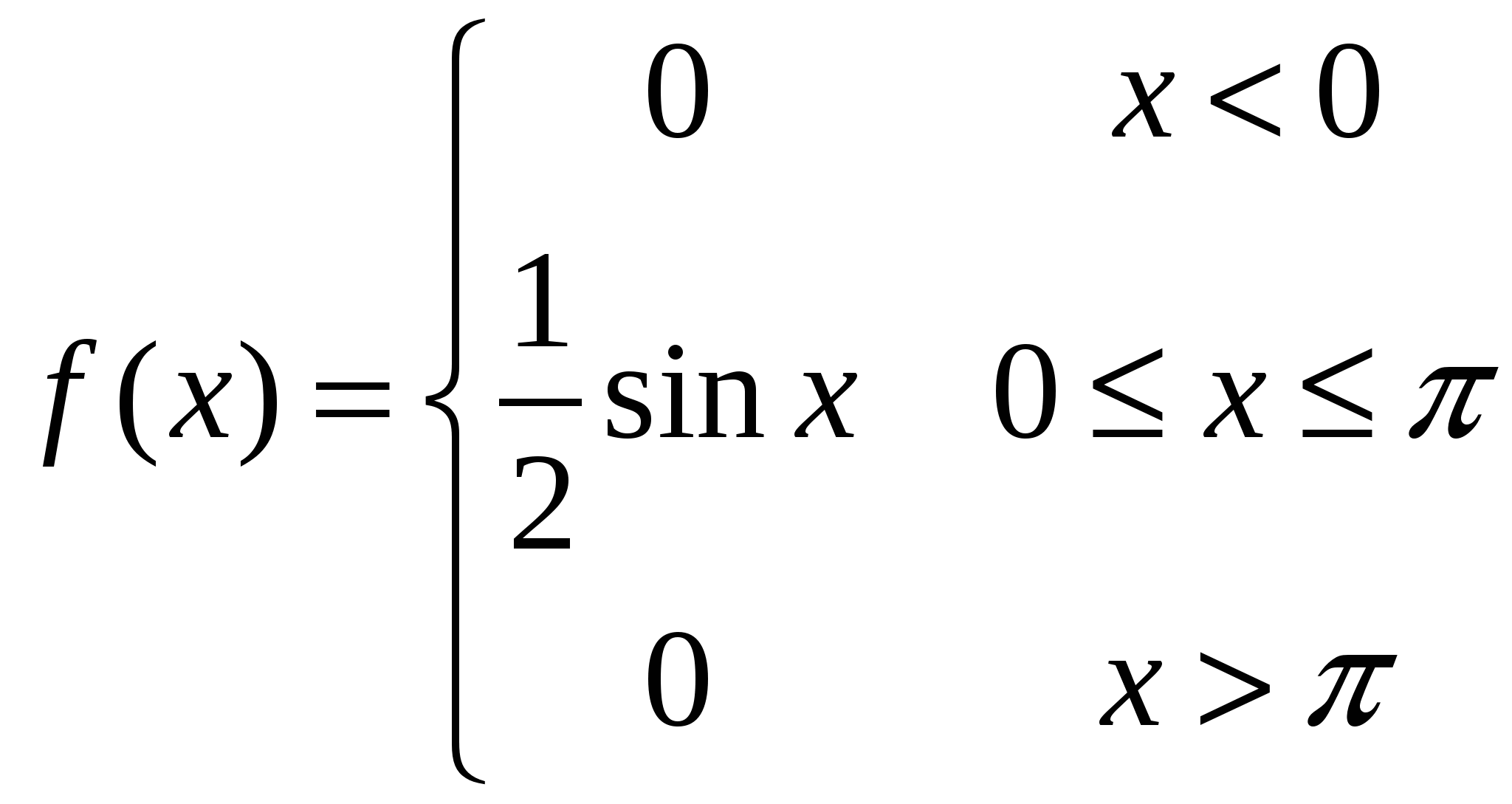
Найти функцию распределения F(x) и построить ее график.график.
Случайная величина X имеет плотность распределения вероятности
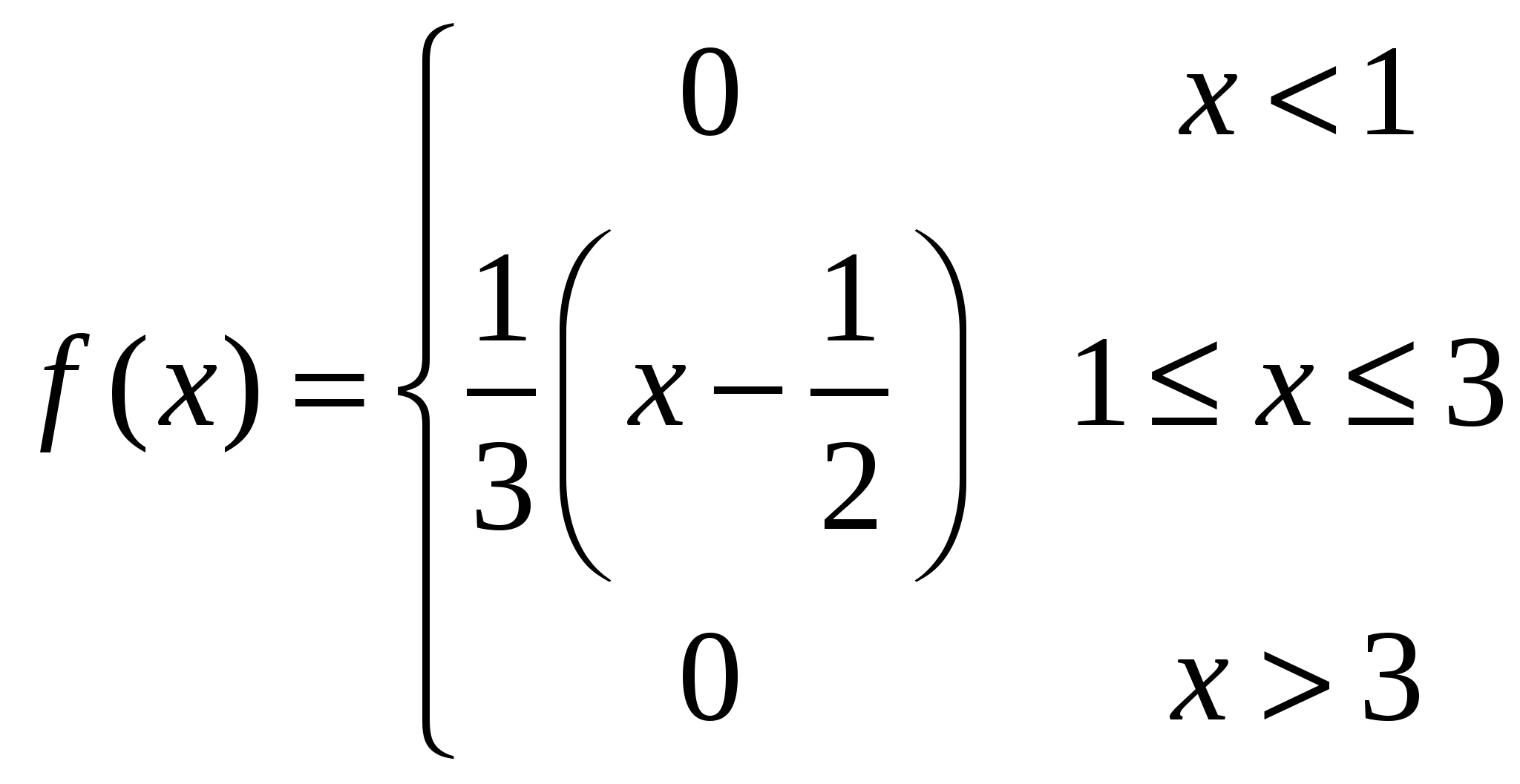
Найти функцию распределения вероятностей и построить ее график
Плотность вероятности непрерывной случайной величины X задана в виде
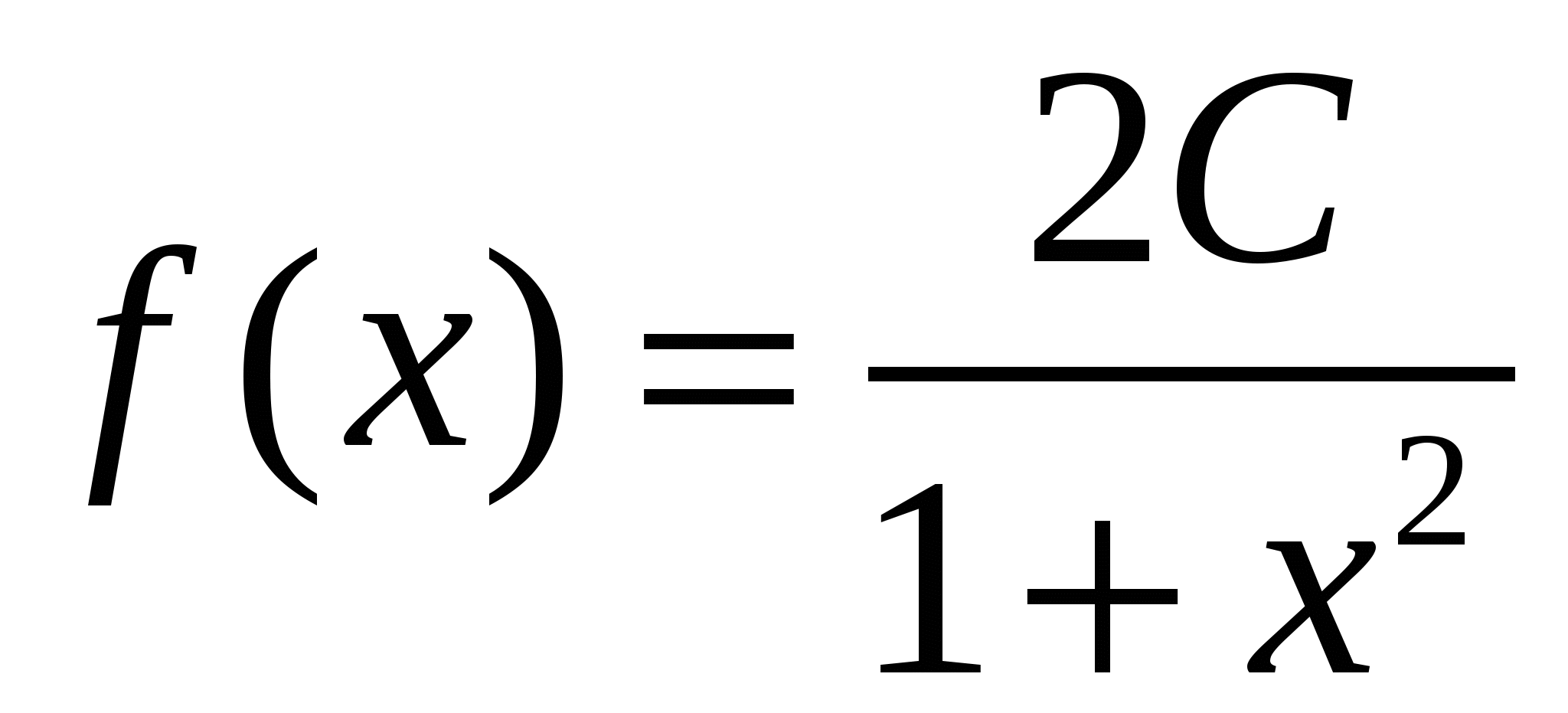 . Найти параметр С. . Найти параметр С.
Плотность вероятности непрерывной случайной величины X задана в интервале (0; π /4) функцией f(x) = Сsin 4х. Вне этого интервала f(x) = 0. Найти параметр С.
Плотность вероятности непрерывной случайной величины X задана в интервале (-π/2; π /2) функцией f(x) = С соs 5 х. Вне этого интервала f(x) = 0. Найти параметр С и определигь вероятность попадания случайной величины X в интервал (0; π /4).
Математическое ожидание и дисперсия. Мода и медиана
Средним значением или математическим ожиданием непрерывной случайной величины X называется значение интеграла
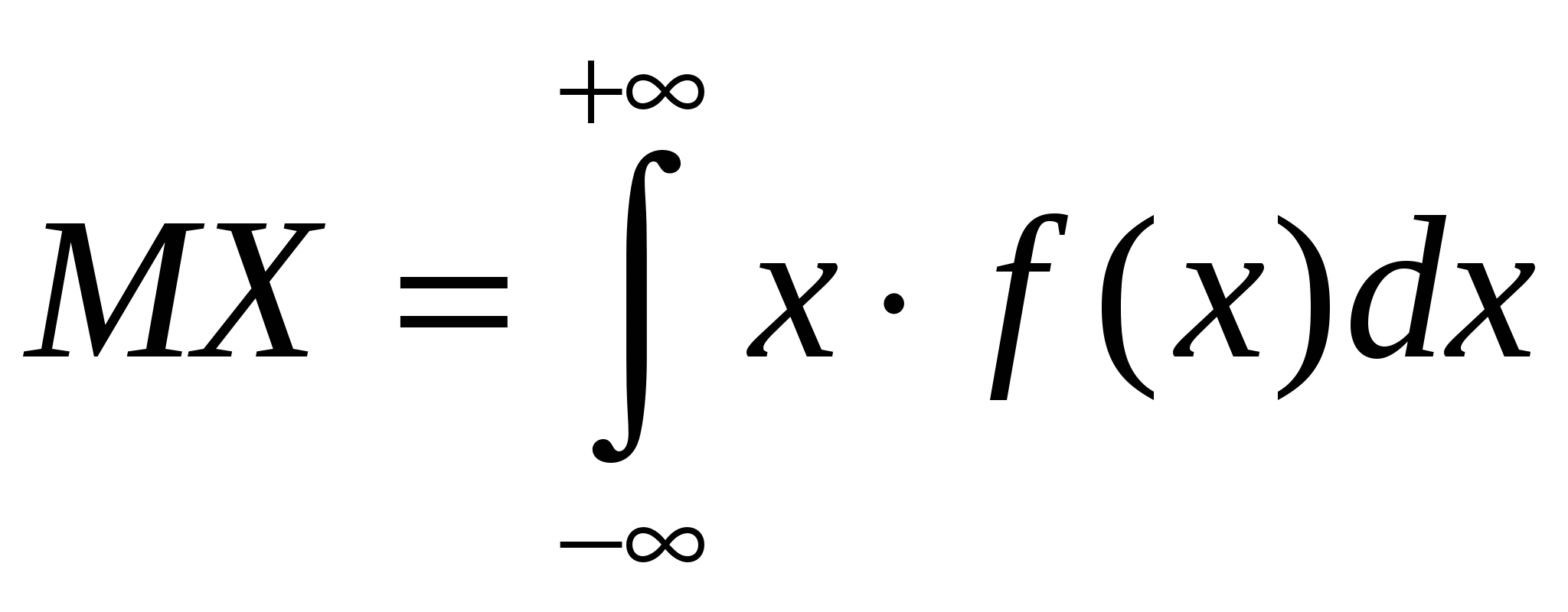 , ,
где f(x) — плотность вероятности.
Дисперсией непрерывной случайной величины X называется значение интеграла
D(X) = М(Х - М(Х))2.
Дисперсию целесообразно вычислять по формуле
D(X) = М(Х2) - (М(Х))2
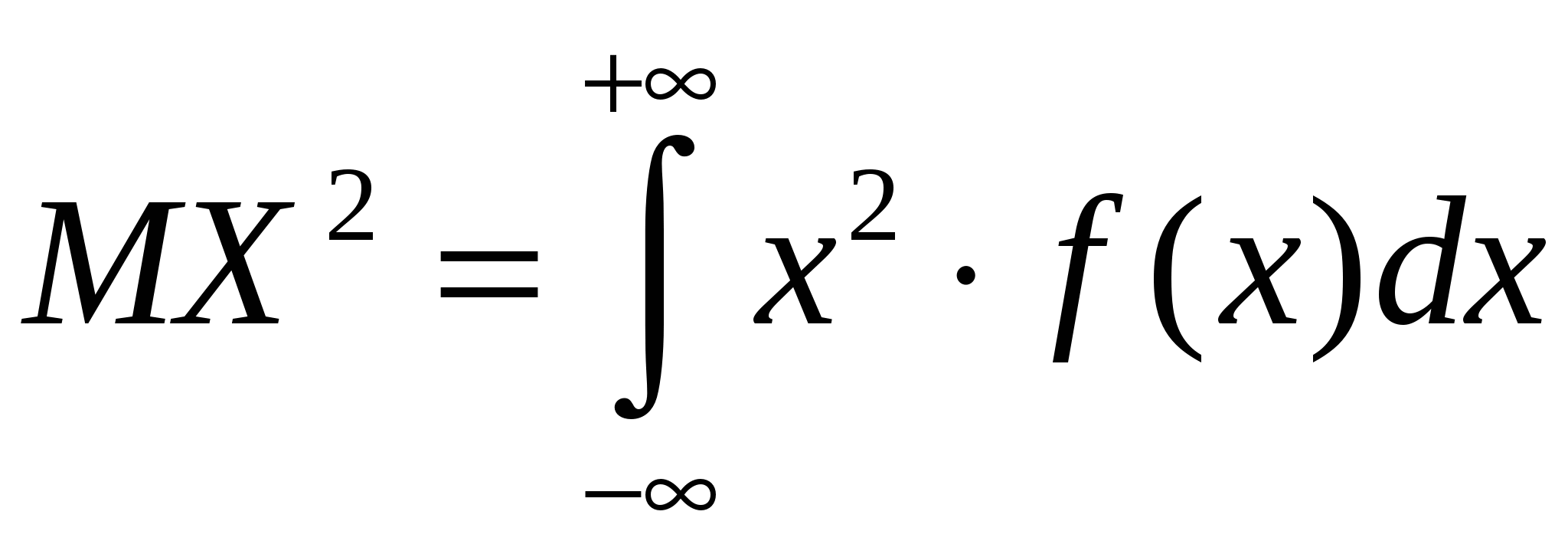
Модой Мо(Х) непрерывной случайной величины X называется такое значение этой величины, плотность вероятности которого максимальна.
Медианой Ме(Х) непрерывной случайной величины X называется такое ее значение, при котором выполняется равенство
Р(Х < Me) =Р(Х > Me).
Случайная величина X задана плотностью вероятности f(x) = х/2 в интервале (0; 2), вне этого интервала f(x) = 0. Найти математическое ожидание величины X.
Случайная величина X задана плотностью вероятности f(x) = х/8 в интервале (0; 4). Вне этого интервала f(x) = 0. Найти математическое ожидание.
Непрерывная случайная величина имеет плотность вероятности f(x)=C в интервале (0;4). Вне этого интервала f(x) = 0. Найти
А)значение константы С,
Б)математическое ожидание случайной величины
В) дисперсию случайной величины
Г) вероятность попадания в интервал 2;5.
Д) на чертеже изобразить график функции плотности вероятности и объяснить геометрический смысл найденной вероятности.
Случайная величина X задана плотностью вероятнос- f(x) = С(х2 + 2х) в интервале (0; 1). Вне этого интервала f(x)=0. Найти параметр С и MX.
Плотность вероятности случайной величины Xимеет вид:
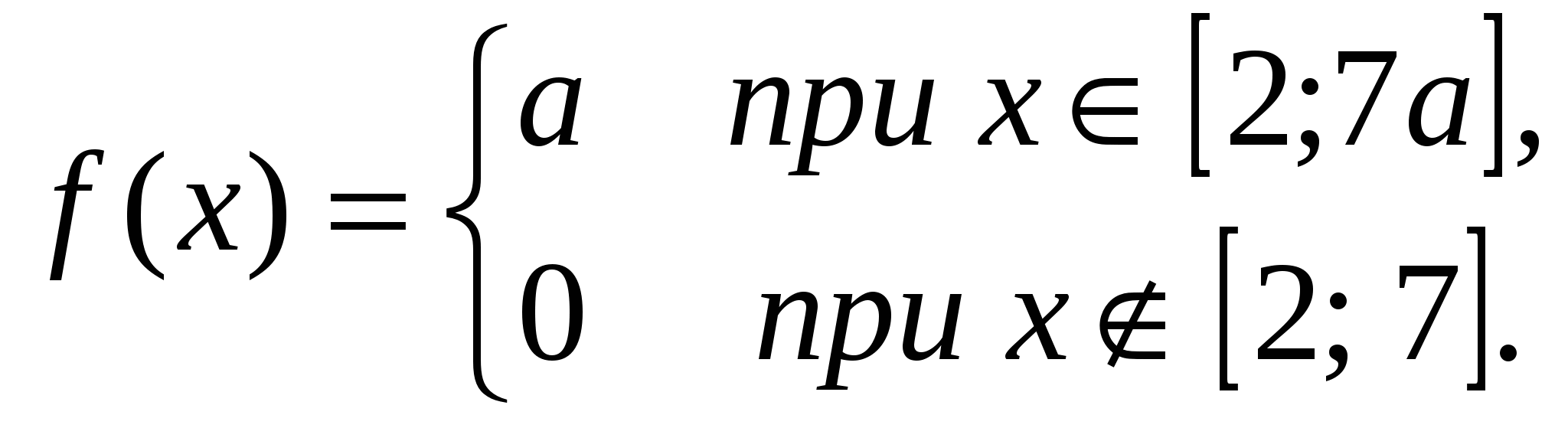
Необходимо:
а) найти параметр a;
б) вычислить математическое ожидание;
в) найти вероятность P(1
г) построить графики функции распределения и плотности вероятности случайной величины X.
Случайная величина X задана плотностью вероятности 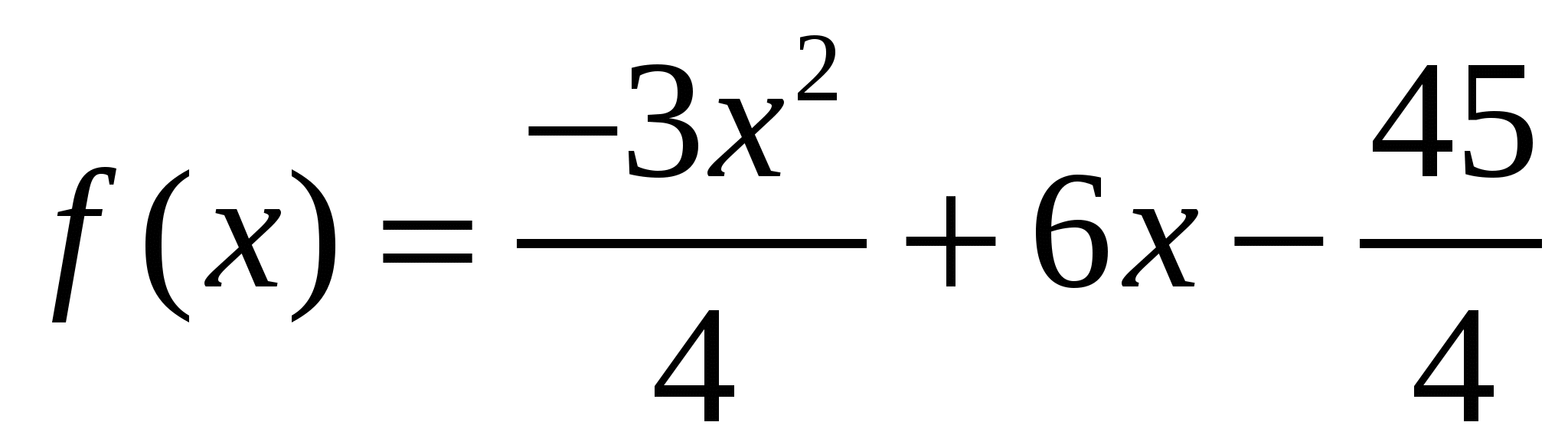 — на интервале (3; 5). Вне этого интервала f(x)=0. — на интервале (3; 5). Вне этого интервала f(x)=0.
Найти моду, медиану и математическое ожидание.
Случайная величина X задана плотностью вероятности 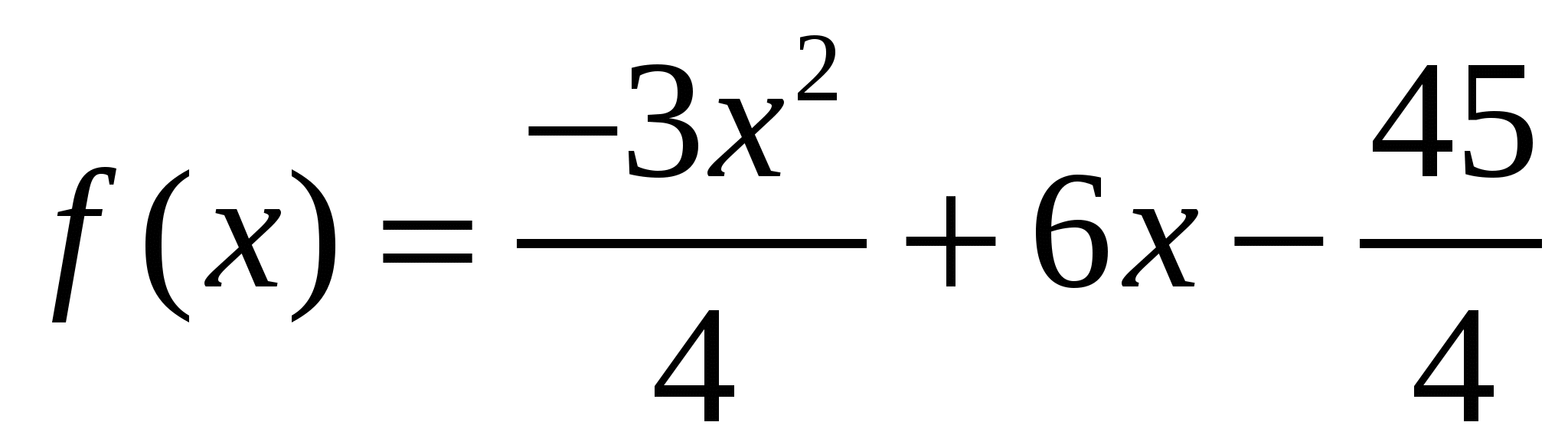 — на интервале (2; 4). Вне этого интервала f(x)=0. — на интервале (2; 4). Вне этого интервала f(x)=0.
Найти моду, медиану и математическое ожидание.
Случайная величина X имеет плотность вероятности
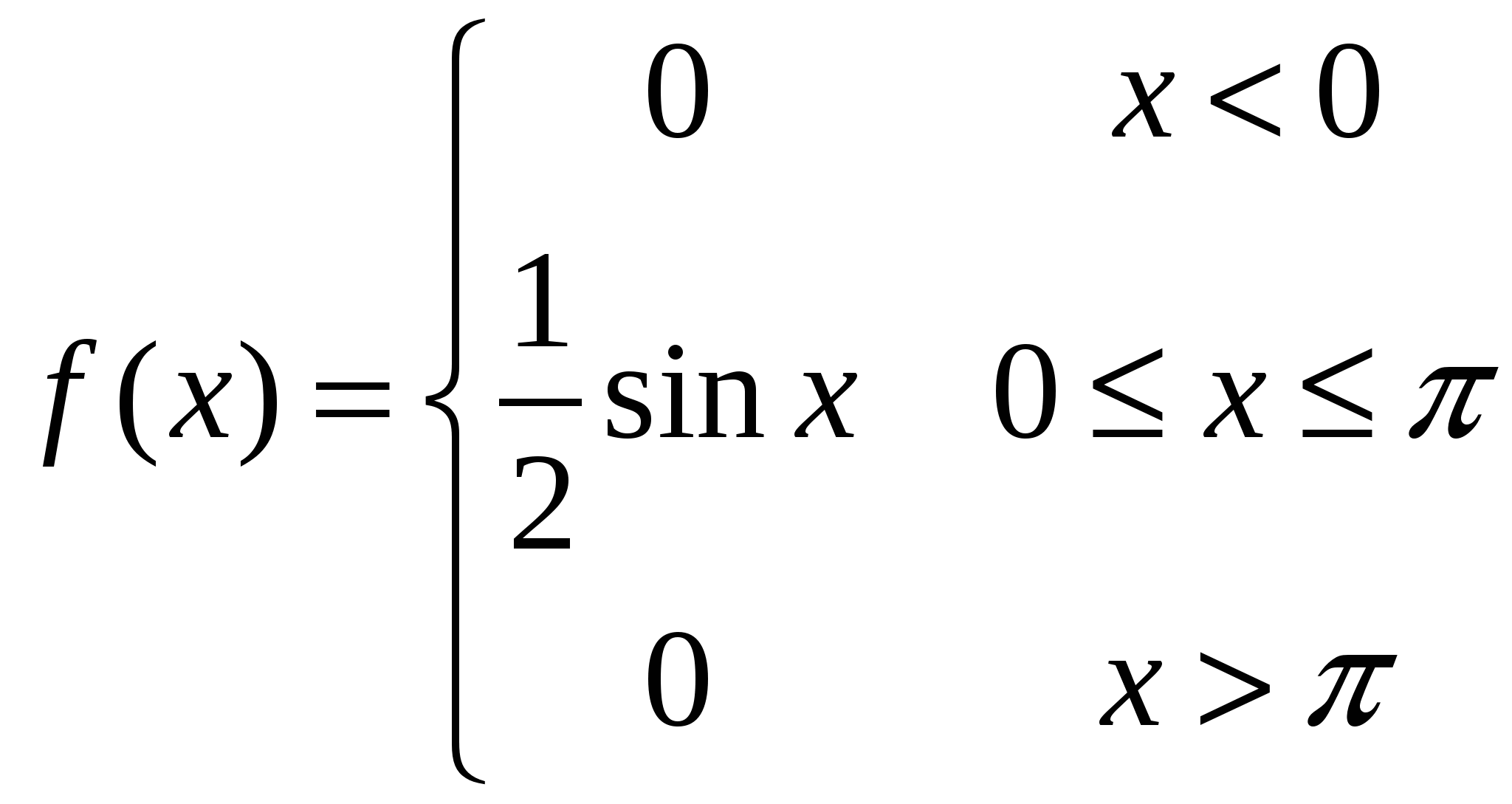
Найти дисперсию случайной величины X.
Задана функция 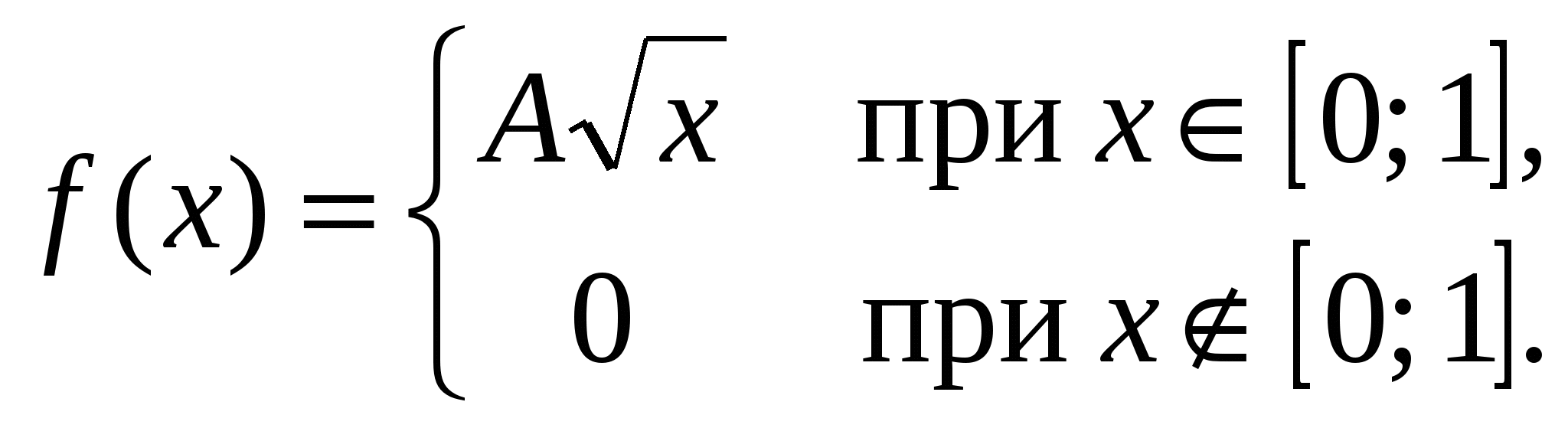
Определить значение параметра A, при котором эта функция задает плотность распределения вероятности некоторой непрерывной CB X. Найти F(x), 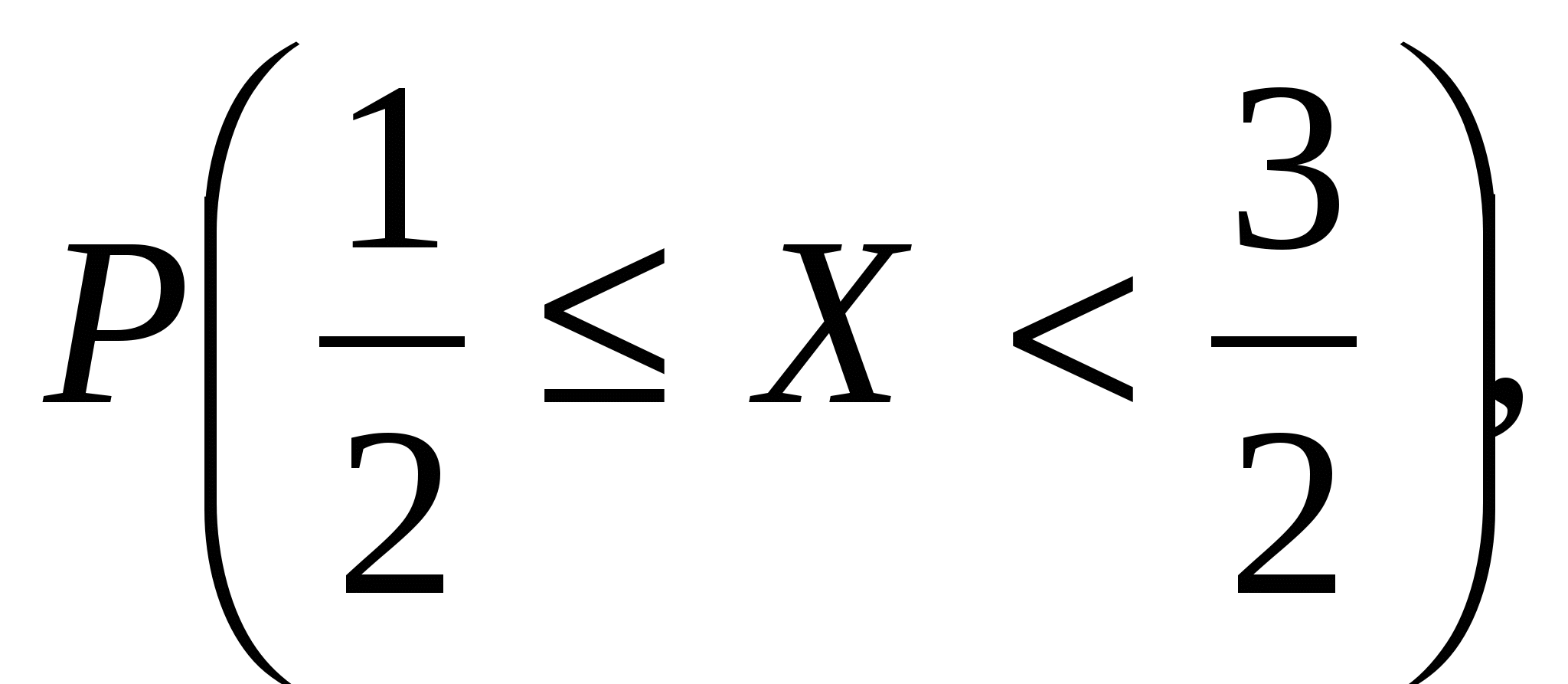 M(X), D(X). Построить график F(x). M(X), D(X). Построить график F(x).
Плотность распределения случайной величины X имеет вид:
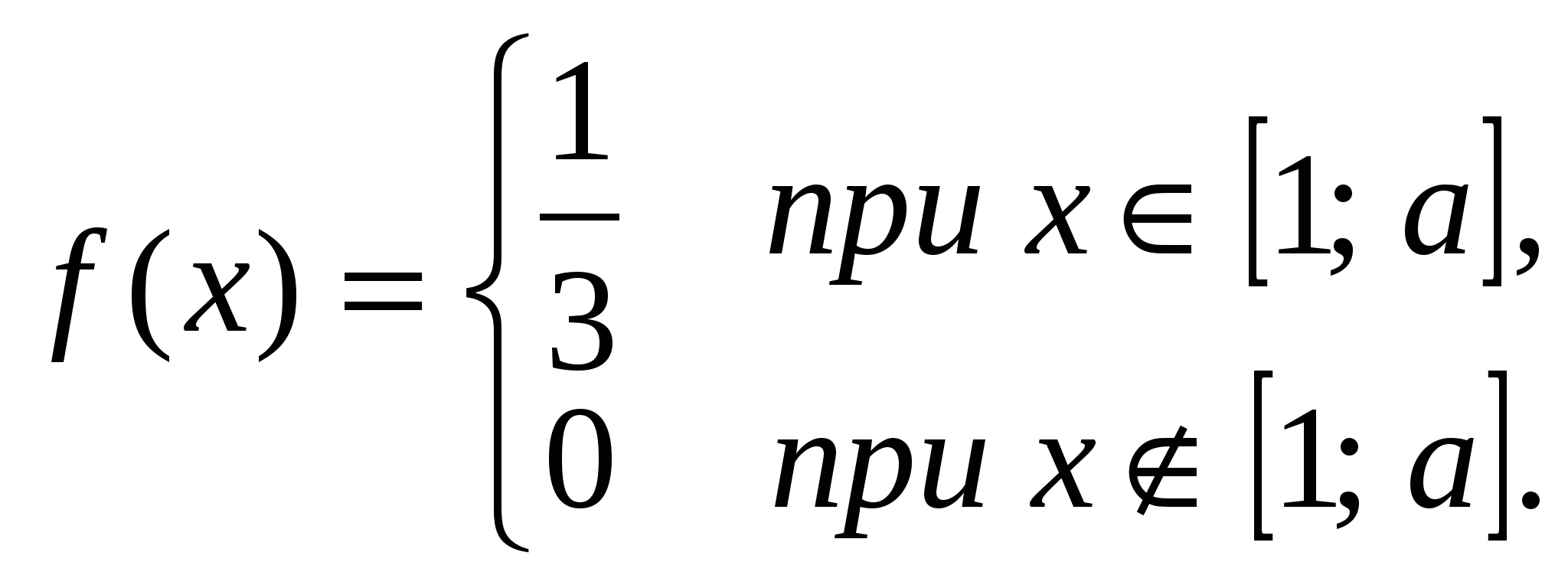
Найти:
а) значение постоянной а;
б) MXи DX;
в) вероятность P(0 X2);
г) функцию распределения F(x), построить ее график.
Плотность распределения случайной величины X имеет вид:
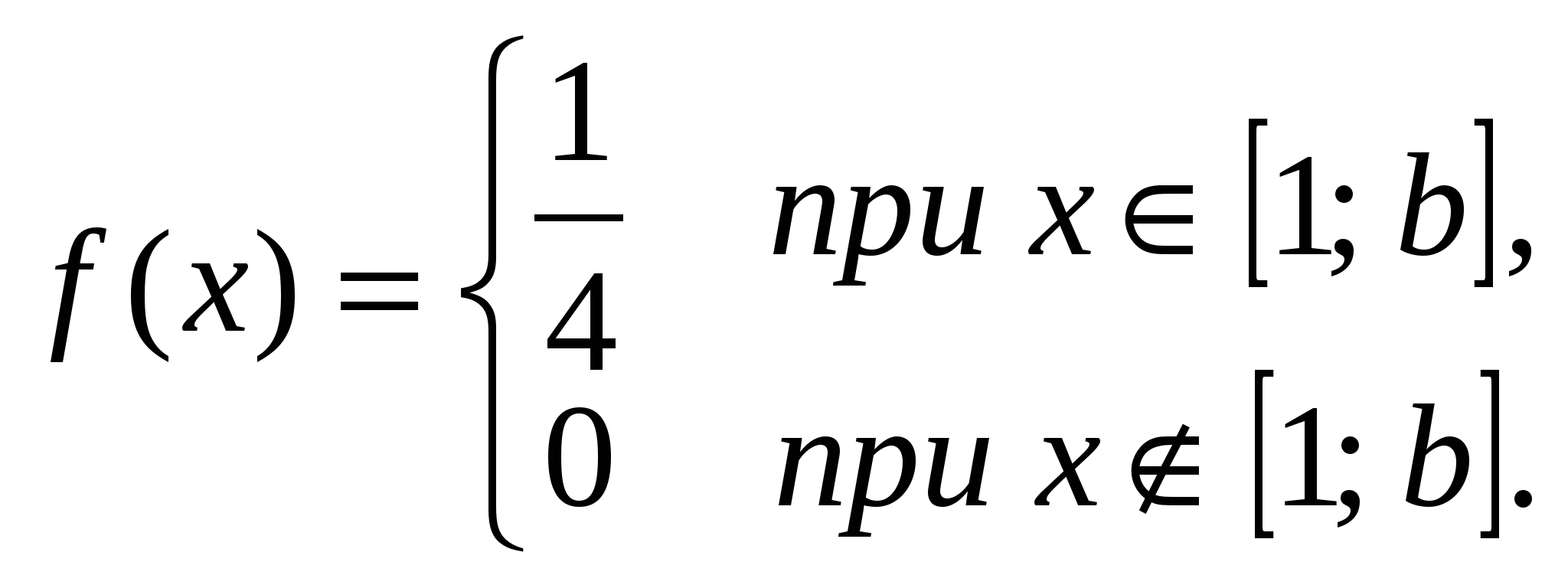
Найти:
а) значение постоянной b;
б) MXи DX;
в) вероятность P(0 X3);
г) функцию распределения F(x), построить ее график.
Плотность вероятности случайной величины Xимеет вид:
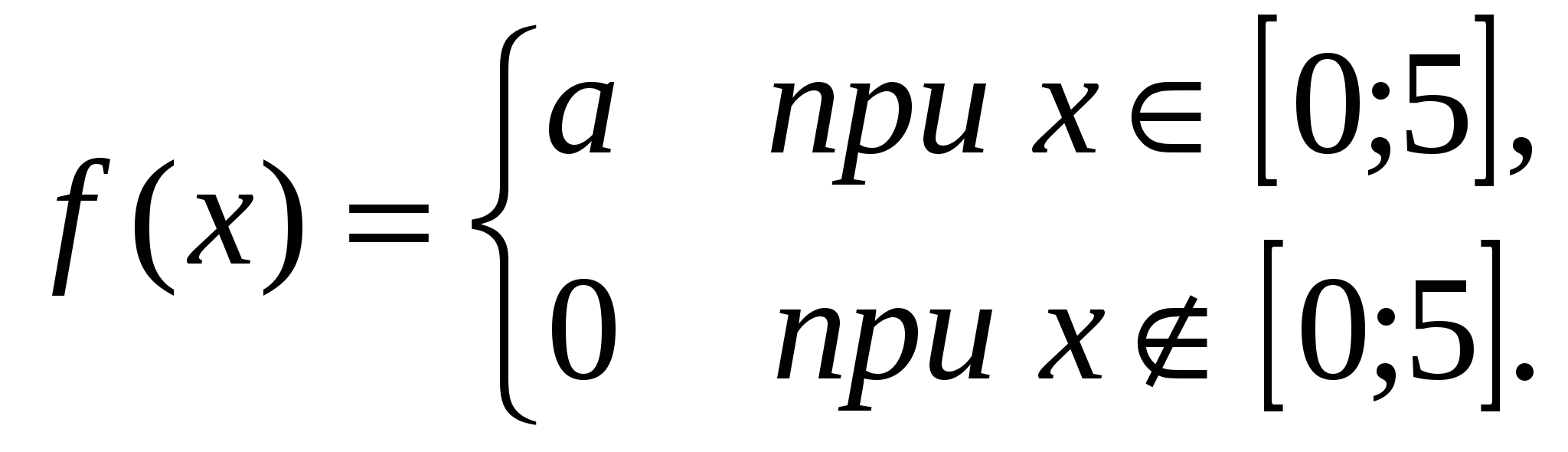
Найти:
а) параметр а;
б) математическое ожидание и дисперсию;
в) P(0
Функция распределения непрерывной случайной величины X имеет вид:
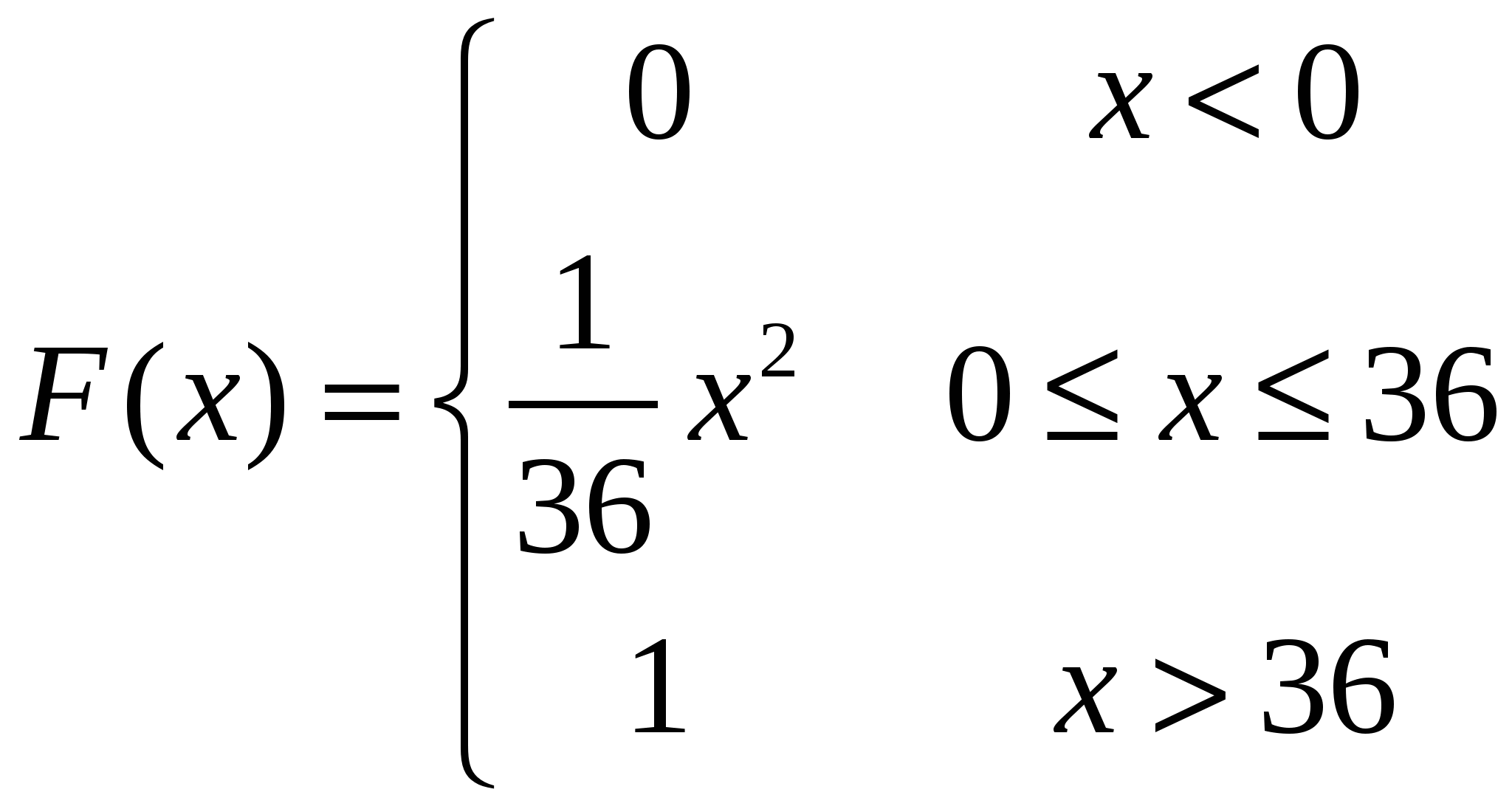
Найти:
а) математическое ожидание М(X);
б) дисперсию D(X);
в) P(0,6
Ежедневная прибыль фирмы «Ой-ой-ой» является случайной величиной с плотностью вероятностей вида
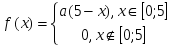 . .
Найти параметр  , математическое ожидание и среднее квадратическое отклонение прибыли. Вычислить вероятность того, что случайная величина попадает в промежуток , математическое ожидание и среднее квадратическое отклонение прибыли. Вычислить вероятность того, что случайная величина попадает в промежуток 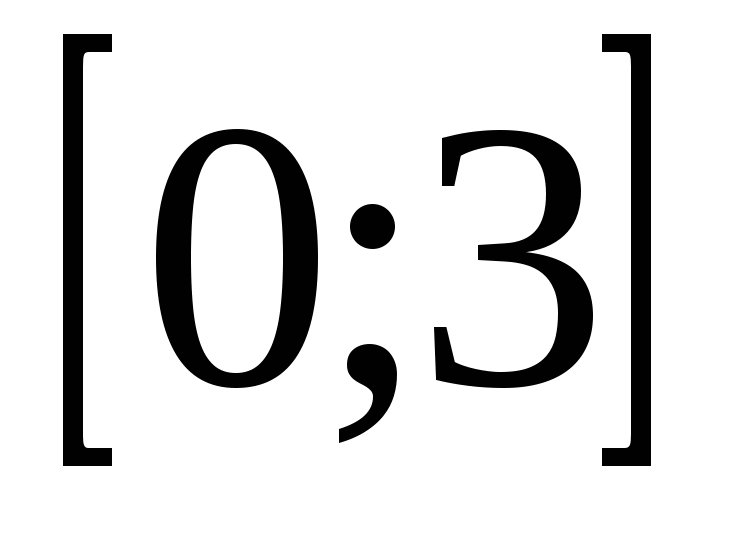 . Построить график . Построить график  , показать на нем , показать на нем 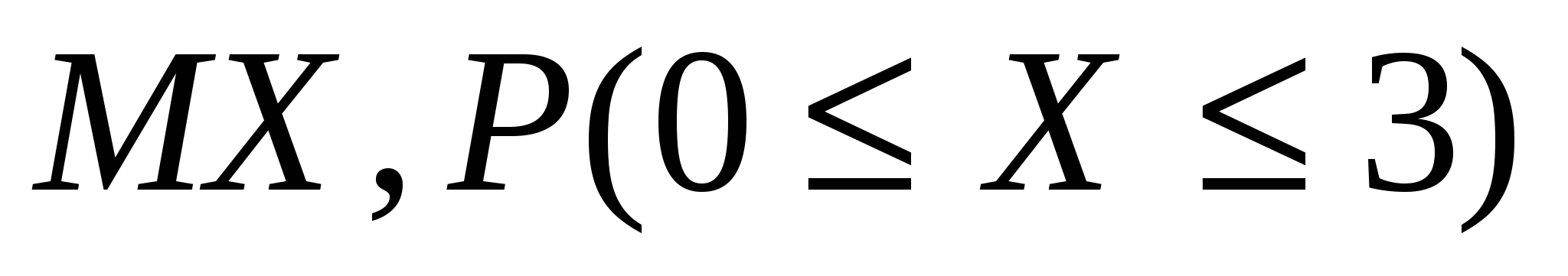 . .
Равномерное распределение
Непрерывная случайная величина называется равномерно распределенной на отрезке [а, b], если ее плотность вероятности имеет вид
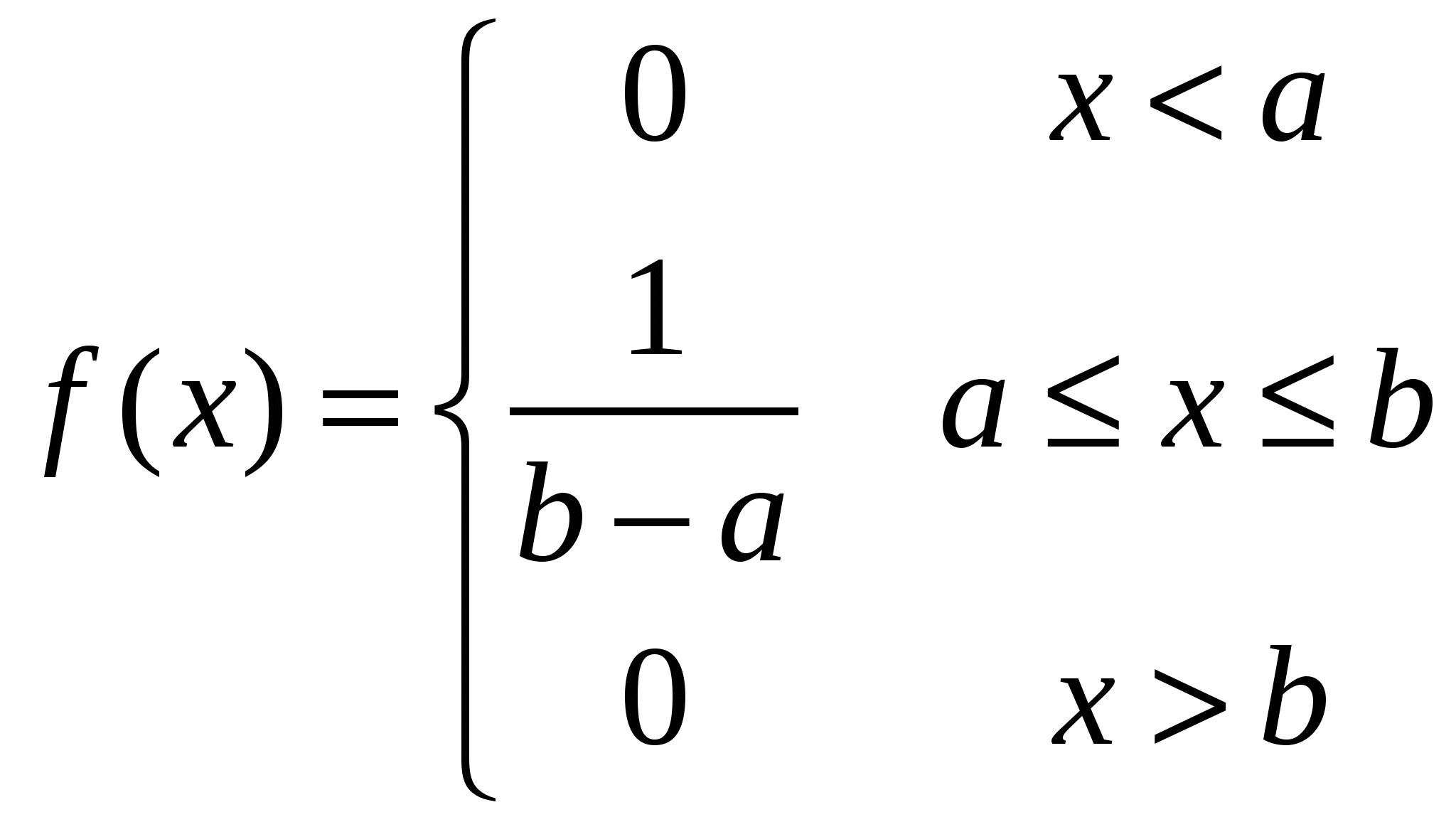
Математическое ожидание и дисперсия равномерно распределенной случайной величины определяются выражениями
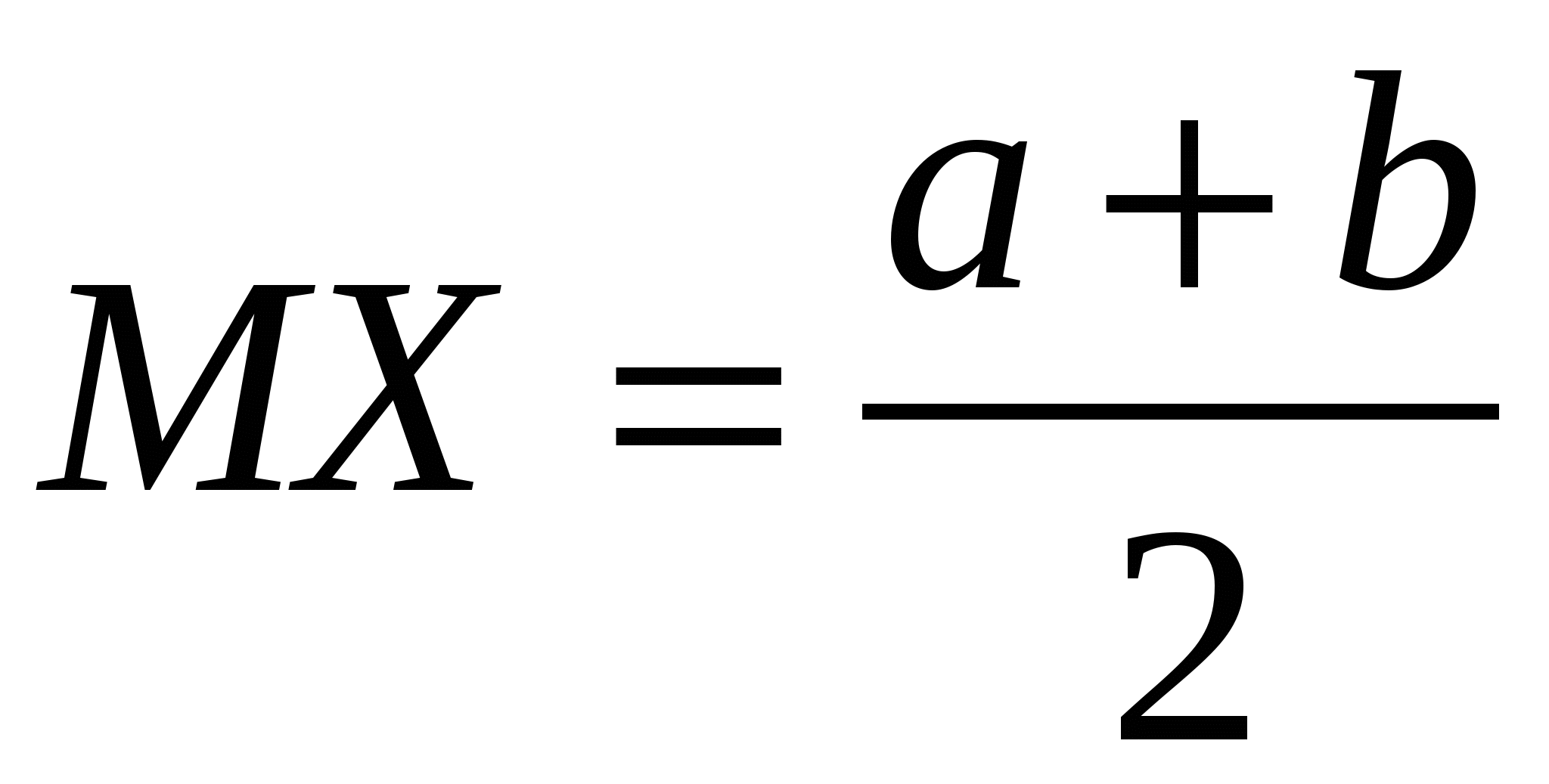 , , 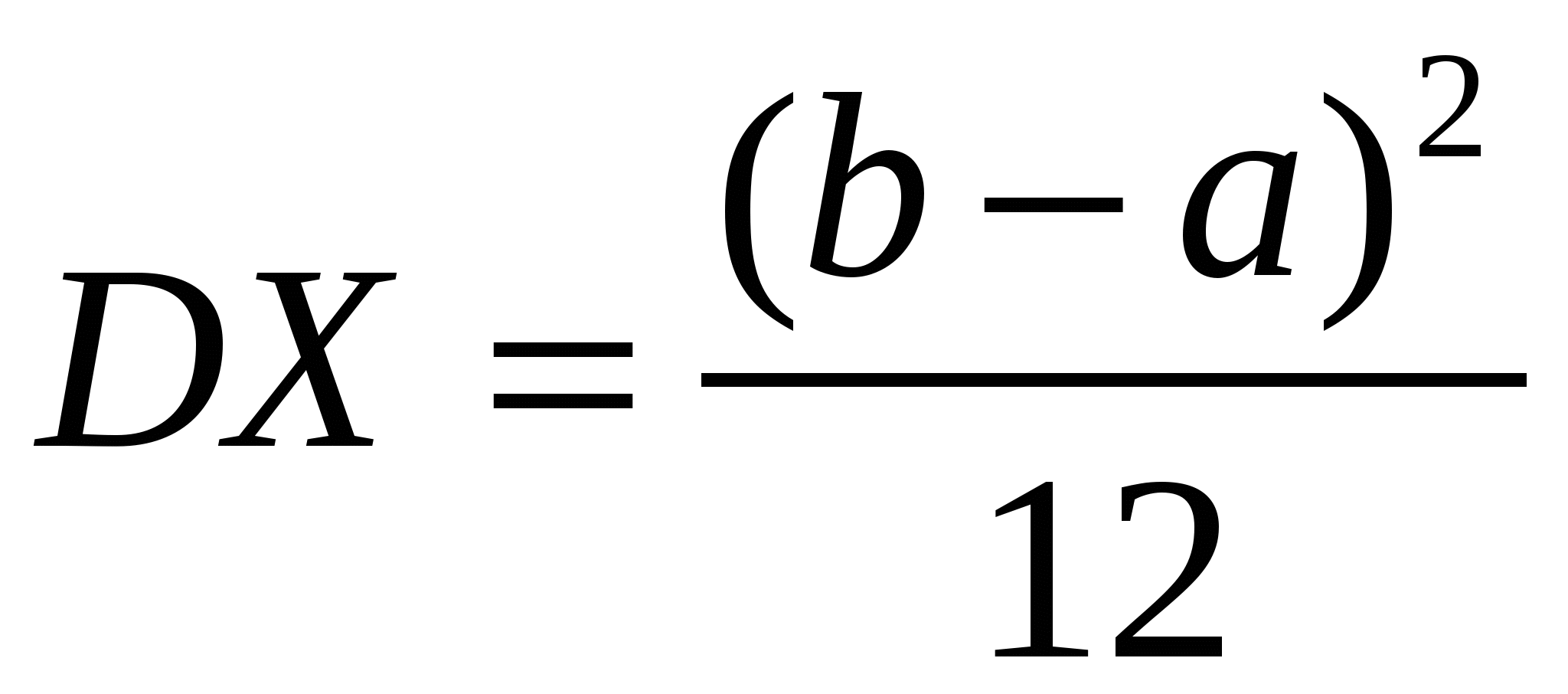
Случайная величина X распределена равномерно на отрезке [1;6]. Найти функцию распределения F(x), математическое ожидание, дисперсию и среднее квадратичное отклонение величины.
Случайная величина X распределена равномерно на отрезке [0;4]. Найти функцию распределения F(x), математическое ожидание, дисперсию и среднее квадратичное отклонение величины.
Автобусы подходят к остановке с интервалом в 5 мин. Считая, чго случайная величина X — время ожидания автобуса — распределена равномерно, найти среднее время ожидания (математическое ожидание) и среднее квадратичное отклонение случайной величины.
Паром для перевозки автомашин через залив подходит к причалу через каждые два часа. Считая, что время прибытия автомашин — случайная величина X — распределена равномерно, определить среднее время ожидания автомашиной прихода парома и дисперсию времени ожидания.
Нормальное распределение
Случайная величина X распределена по нормальному закону, если ее функция плотности распределения вероятностей имеет вид
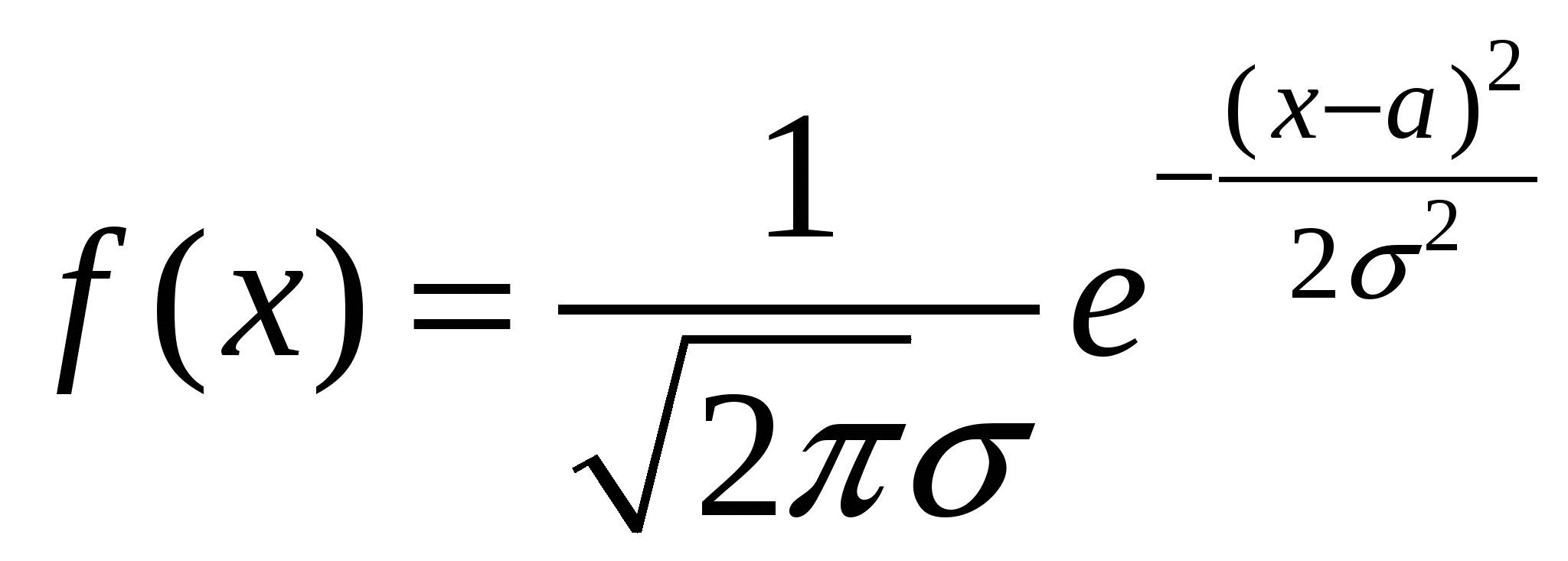
где a — математическое ожидание;
 — среднее квадратичное отклонение. — среднее квадратичное отклонение.
Вероятность попадания случайной величины в интервал (а, b) находится по формуле
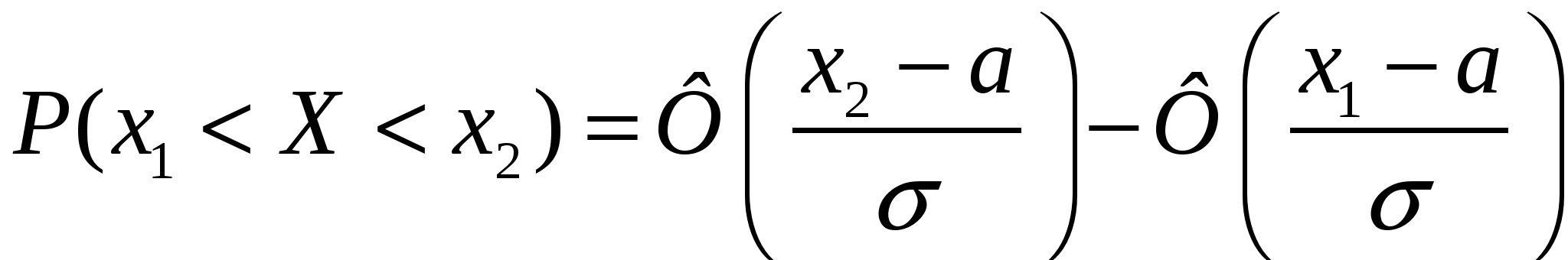 , где Ф(x)= , где Ф(x)= 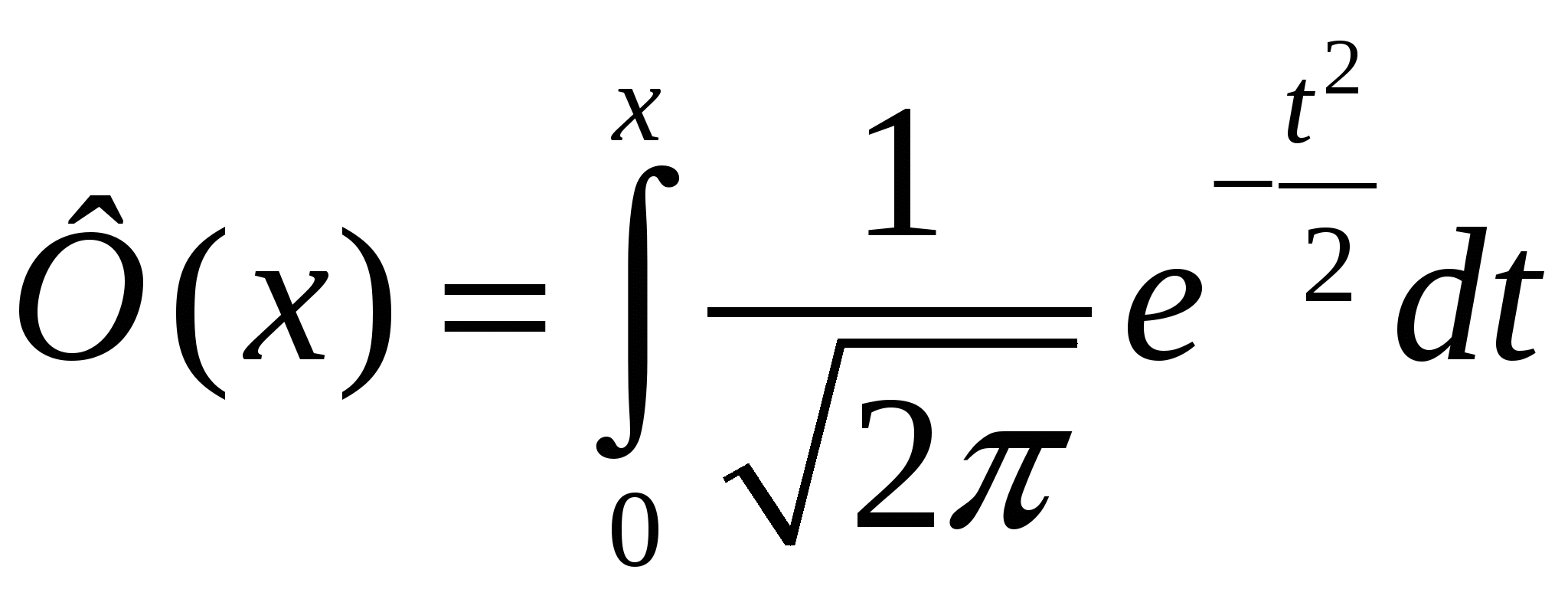 — функция Лапласа. — функция Лапласа.
Значения функции Лапласа для различных значений x можно найти в справочниках.
Математическое ожидание нормально распределенной случайной величины X равно 5, дисперсия равна 9. Написать выражение для плотности вероятности.
Найти M(4X– 3) D(4X– 3), если плотность случайной величины Xимеет вид:
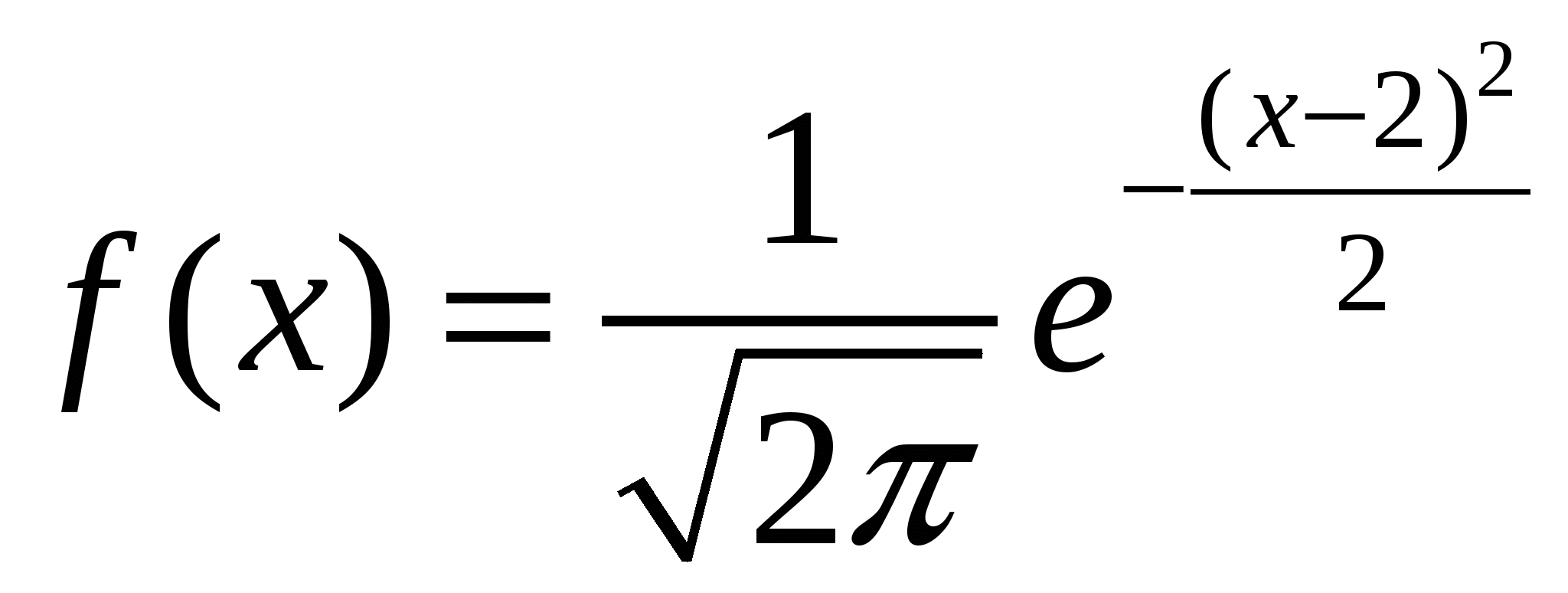
Математическое ожидание и среднее квадратичное отклонение нормально распределенной случайной величины X соответственно равны 12 и 2. Найти вероятность того, что случайная величина примет значение, заключенное в интервале (14; 16).
Случайная величина нормально распределена. Известно, что MX=-2, DX=1 Найти:
а) плотность вероятности случайной величины и ее значения в точках x=-1, x=0, x=2
б) вероятности P(-21)
Имеется случайная величина X, распределенная по нормальному закону, математическое ожидание которой равно 20, среднее квадратичное отклонение равно 3. Найти симметричный относительно математического ожидания интервал, в который с вероятностью р — 0,9972 попадет случайная величина.
Случайная величинах распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратичным отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,954 попадет случайная величина.
Известно, что средний расход удобрений на один гектар пашни составляет 80 кг, а среднее квадратичное отклонение расхода равно 5 кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадает с вероятносгью 0,98.
Математическое ожидание нормально распределенной случайной величины — количества сыра, используемого для изготовления 100 бутербродов,— равно 1кг. Известно, что с вероятностью 0,96 расход сыра на изготовление 100 бутербродов составляет от 900 до 1100 г. Определить среднее чное отклонение расхода сыра на 100 бутербродов.
Уровень воды в реке – это нормально распределенная случайная величина со средним значением 2,5 м и стандартным отклонением 20 см. Оценить вероятность того, что в наудачу выбранный день:
а) уровень превысит 3 м; б) окажется в пределах от 2,2 м до 2,8 м.
Суточное потребление электроэнергии в населенном пункте является нормально распределенной случайной величиной с математическим ожиданием 2000 кВт/ч и дисперсией 20000. Найти вероятность того, что в ближайший день расход электроэнергии в населенном пункте будет от 1500 до 2500 кВт/ч
Месячная прибыль компании Мобильные телефоны Средиземья (МТС) является нормальной случайной величиной с математическим ожиданием 1 000 в валюте Средиземья и дисперсией 250 000. Чему равна вероятность того, что прибыль компании окажется:
а) в пределах от 500 до 2 000?; б) более 1 250?
Построить график плотности данного нормального распределения и указать на графике область, соответствующую вероятности из пункта а)
Доход фирмы за месяц представляется нормально распределенной случайной величиной со средним значением 3 млн. долл. и средним квадратическим отклонением 0.5 млн. долл. . Найдите вероятность того, что в данном месяце доход фирмы будет более 4 млн. долл. Напишите формулу плотности распределения этой случайной величины, нарисуйте ее график и покажите на нем вычисленную вероятность.
Локальная и интегральная теоремы Муавра-Лапласса
Аудиторную работу по теории вероятности успешно выполнило 50% студентов. Найти вероятность того, что из 150 студентов успешно выполнят:
а) 50 студентов;
б) не менее 50 студентов;
в) от 50 до 90 студентов.
Хлебокомбинат выпускает 90% продукции первого сорта. Какова вероятность того, что из 400 изделий хлебокомбината первосортных окажется не менее 380?
Какова вероятность, что среди 730 пассажиров поезда:
а) четверо родилось 23 февраля;
б) никто не родился 22 июня?
Вероятность выпуска бракованных деталей равна 0,2. Найти вероятность того, что среди 120 выпущенных деталей будет не менее 100 стандартных.
На потоке 120 студентов. Вероятность того, что выбранный случайным образом студент выполнит нормативы комплекса ITO третьей ступени, равна 0,7. Определить вероятность того, что не менее 75 студентов выполнят эти нормативы.
В некоторой местности из каждых 100 семей 80 имеют автомобиль. Найти вероятность того, что из произвольно взятых в этой местности 400 семей автомобиль имеют от 310 до 332 семей.
Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.
На заводе изготавливается в среднем 75% деталей отличного качества. За час было изготовлено 400 деталей. Найти вероятность того, что среди них ровно 280 деталей отличного качества.
Вероятность рождения мальчика равна 0,512. Найдите
1) вероятность того, что среди 100 новорожденных будет ровно 51 мальчик.
2) вероятность того, что из 500 новорожденных в регионе мальчиков не менее 250?
В пути повреждается в среднем каждое десятое изделие. Определите вероятность того, что в партии из 500 изделий поврежденных окажется от 50 до 70 изделий.
При данном технологическом процессе 85% всей произведенной продукции является высшим сортом. Произведено 200 изделий. Какова вероятность того, что более 150 изделий будут изделиями высшего сорта? Найти наивероятнейшее число изделий высшего сорта.
Произведено 600 изделий. Вероятность брака для одного изделия
равна 0.2. Найти вероятность того, что количество бракованных изделий превзойдет 400. Найти наивероятнейшее число бракованных изделий.
Из винтовки произведено 900 выстрелов. Вероятность попадания в мишень при одном выстреле равна 0.7. Найти вероятность того, что произойдет ровно 555 попаданий. Найти вероятность того, что произойдет менее 800 попаданий. Найти наивероятнейшее число попаданий.
Город ежедневно посещает 1000 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно быть для этого в его ресторане?
Небольшой город ежедневно посещают 100 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью приблизительно 0,99 все пришедшие в его ресторан туристы могли там одновременно пообедать. Сколько мест должно для этого быть в его ресторане?
Вероятность попадания в цель из скорострельного орудия при отдельном выстреле равна 0,75. Найти вероятность того, что при 300 выстрелах число попаданий будет не менее 210, но не более 230 раз.
В гипермаркете «Большая Калоша» на понедельник объявлена рекламная акция: в среднем каждый третий покупатель получит в подарок сумку в виде калоши. В понедельник в магазине побывали 2500 покупателей. а) Какова вероятность, что сумки в подарок получат более 800 человек? б) Найти наивероятнейшее число покупателей, получивших подарок, и вероятность того, что подарки получат наивероятнейшее число покупателей.
Математическая статистика
В задачах 197- 204 по выблрке выполнить следующие задания:
Построить ряд распределения выборки.
Построить полигон относительных частот.
Вычислить размах выборки.
Вычислить выборочное среднее
Вычислить дисперсию
6. Вычислить среднеквадратичное отклонение
Измерение роста детей младшей группы детского сада представлено выборкой: 92, 96, 95, 96, 94, 97, 98, 94, 95, 96.
3а семь месяцев предприятие получало ежемесячную прибыль (в у.е.):
2, 3, 2, 4, 3, 5, 4.
За 6 месяцев работы сборочной автоматизированной линии получены такие данные по количеству аварий за каждый месяц работы: 2, 2, 2, 1, 4.
3а десять месяцев работы малое предприятие «Воробышек» получало ежемесячную прибыль (в у.е.): 2, 4, 7, 4, 5, 4, 5, 7, 3, 3.
Ежедневный доход казино «Версаль» составил за 7 дней ряд значений:
2, 3, 4, 1, 5, 6, 2 (в условных единицах).
3а десять дней работы малое предприятие «Дюймовочка» получало дневную прибыль (в у.е.): 4, 5, 8, 5, 9, 3, 4, 3, 3, 3.
3а семь месяцев предприятие получало ежемесячную прибыль (в у.е.):
3, 3, 4, 4, 6, 5, 6.
3а десять месяцев работы малое предприятие «Семь гномов» получало ежемесячную прибыль (в у.е.): 3, 3, 5, 6, 7, 3, 4, 4, 6, 6.
Имеются следующие данные о размерах основных фондов (в млн. руб.) 30 предприятий:
4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0; 2,8; 7,3; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8; 9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.
Построить интервальную таблицу частот с шириной интервала 2 (млн. руб.).
Построить гистограмму частот.
Вычислить размах выборки.
Вычислить выборочное среднее
Вычислить дисперсию
Вычислить среднеквадратичное отклонение
Дана выборка выручки магазина за 30 дней (тыс. руб.)
55 71 66 74 71 70 68 76 75 73 65 75 73 70 67
59 63 68 65 65 81 69 64 57 58 68 70 71 71 71
Построить интервальную таблицу частот с числом интервалов 5 (тыс. руб.).
Построить гистограмму частот.
Вычислить размах выборки.
Вычислить выборочное среднее
Вычислить дисперсию
Вычислить среднеквадратичное отклонение
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb.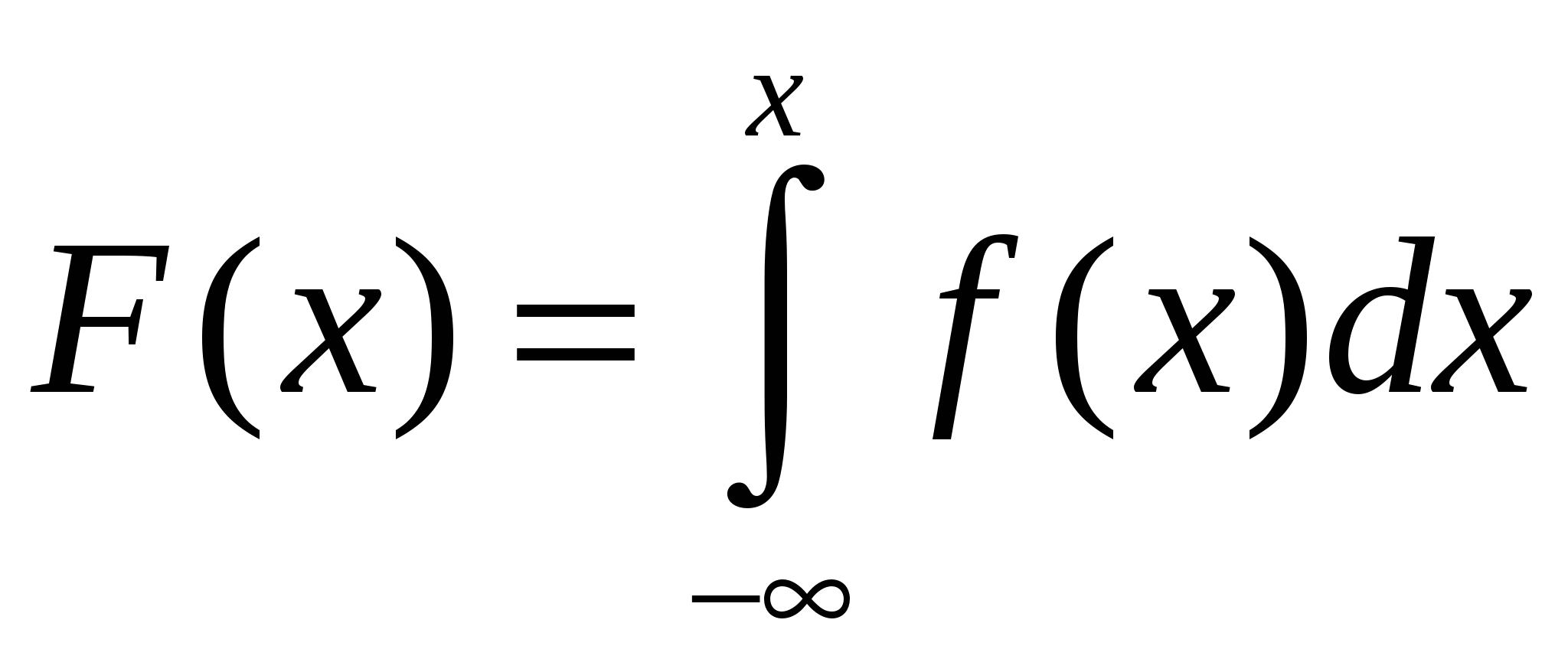
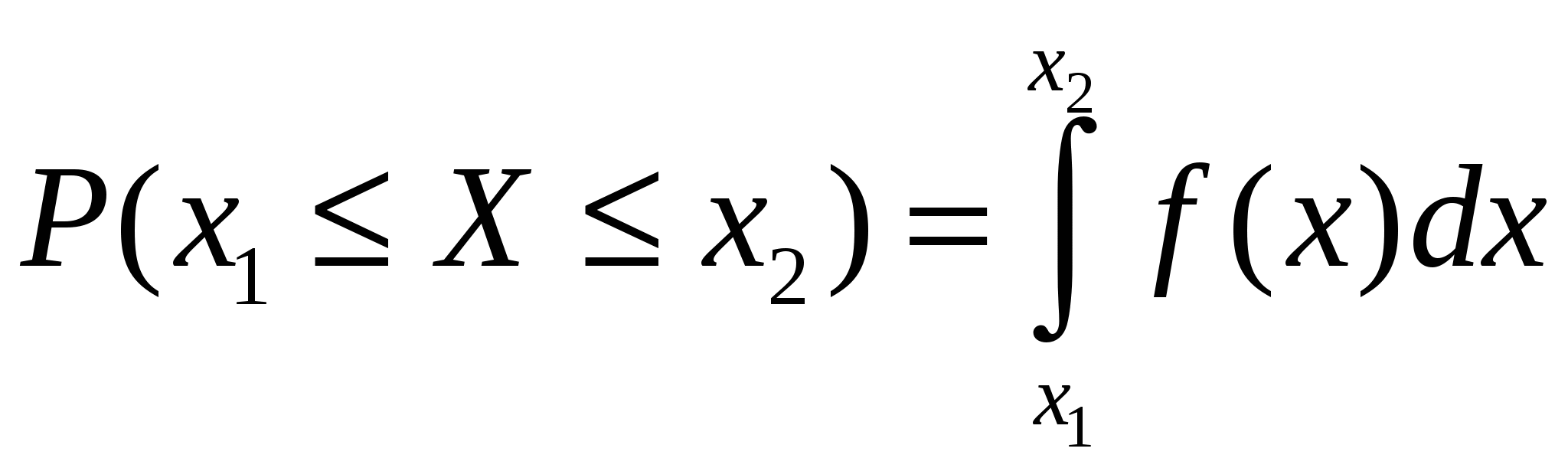 или
или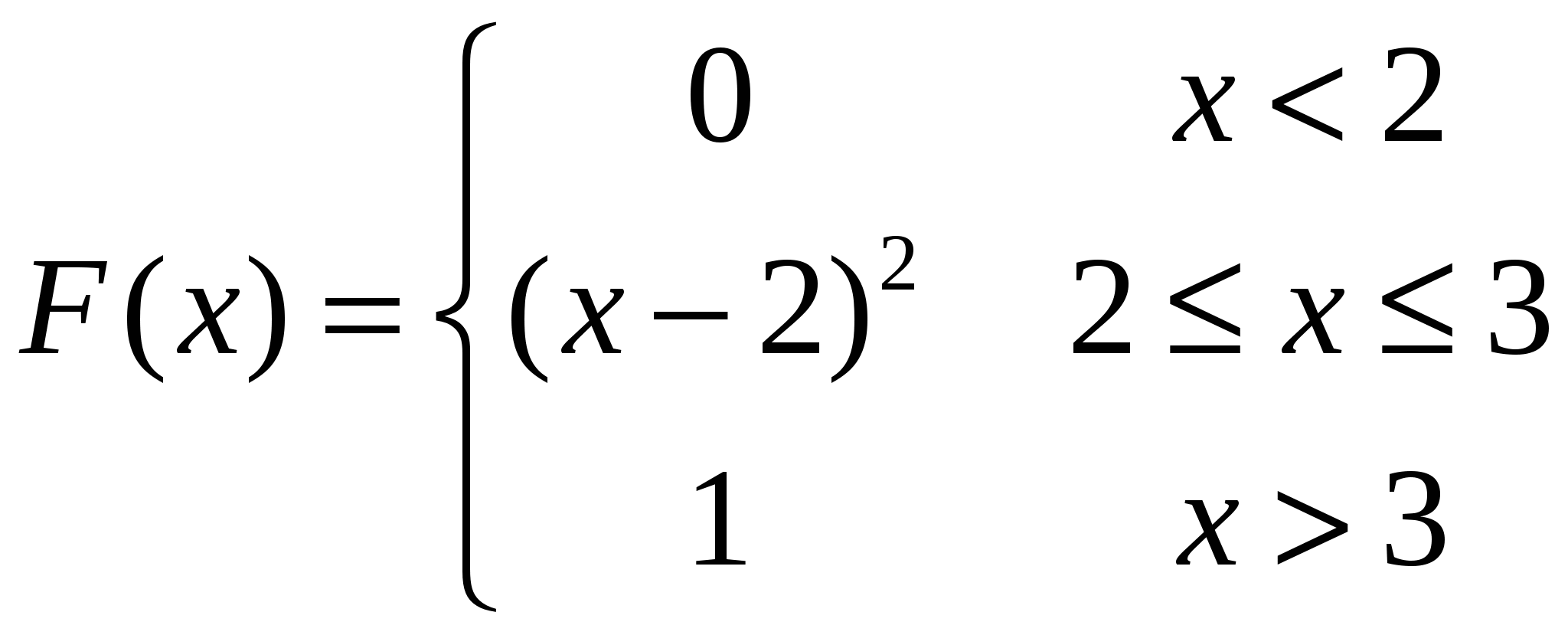
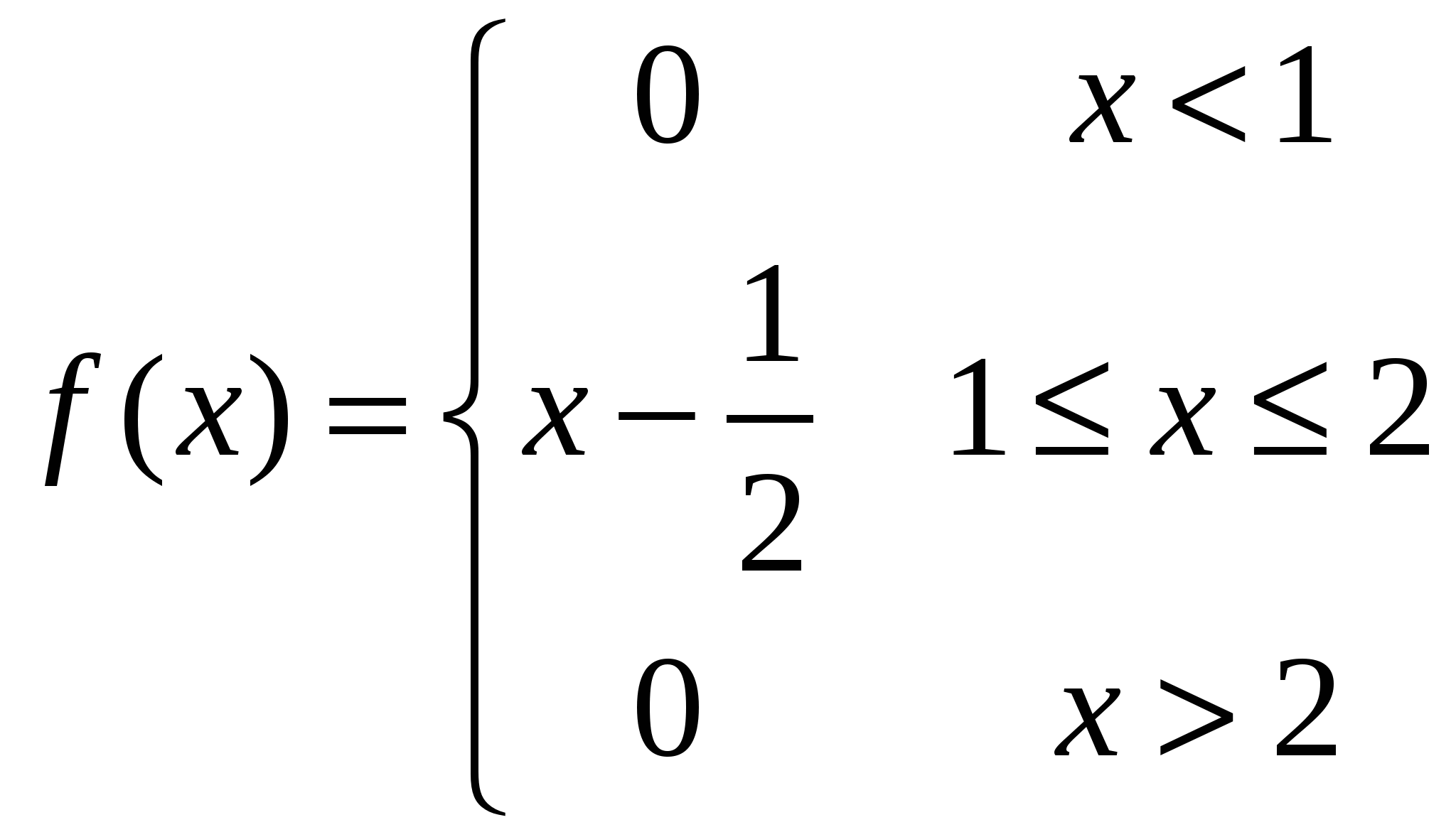
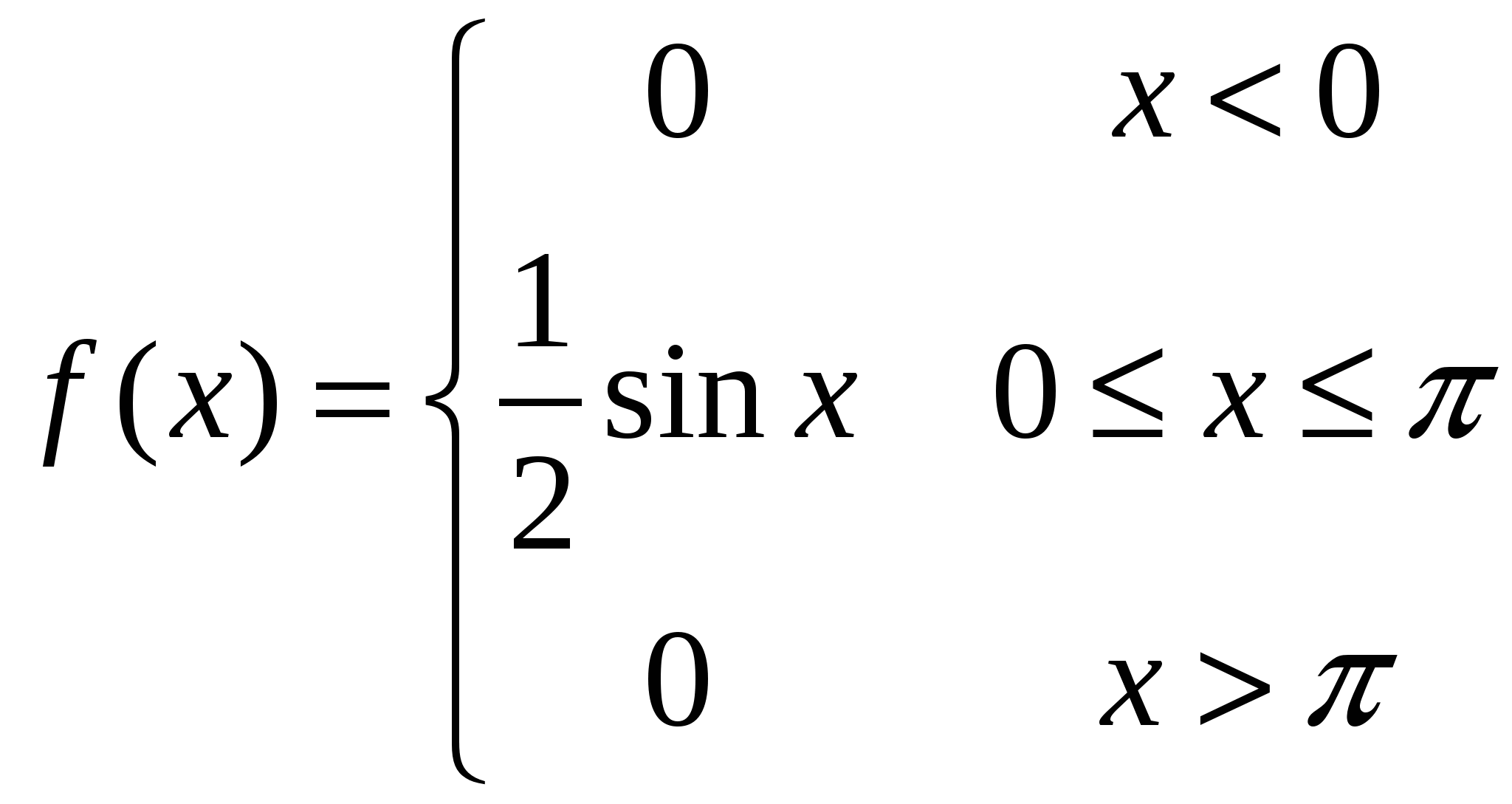
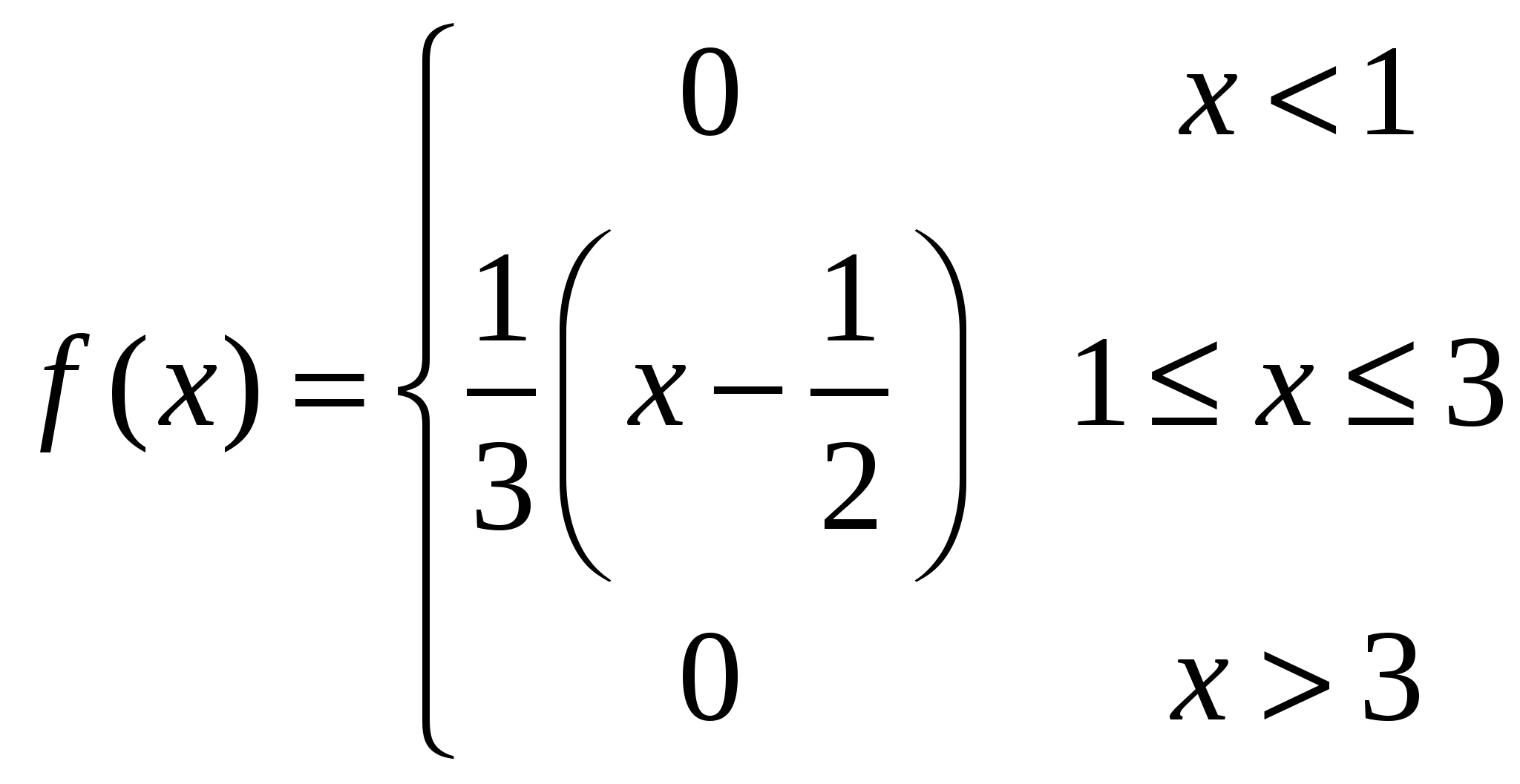
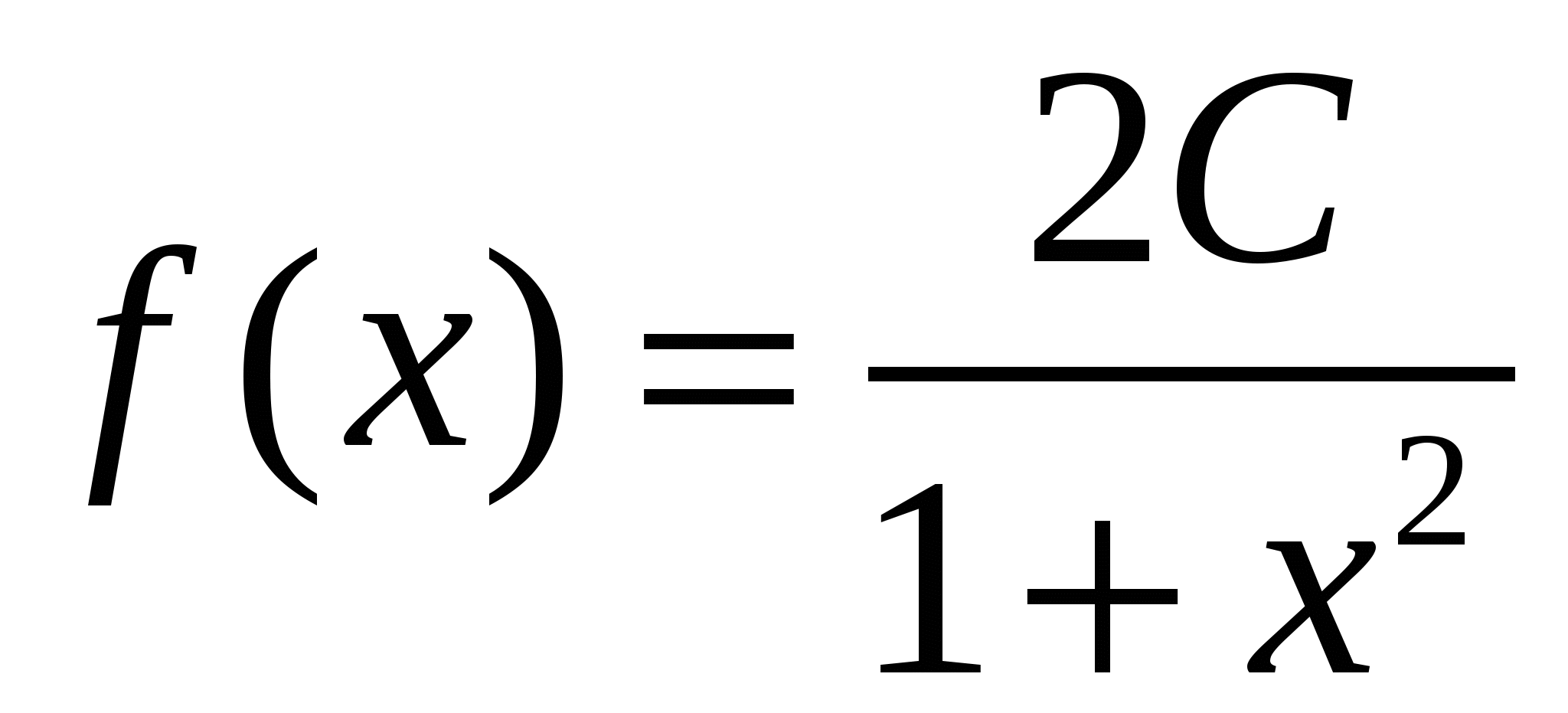 . Найти параметр С.
. Найти параметр С.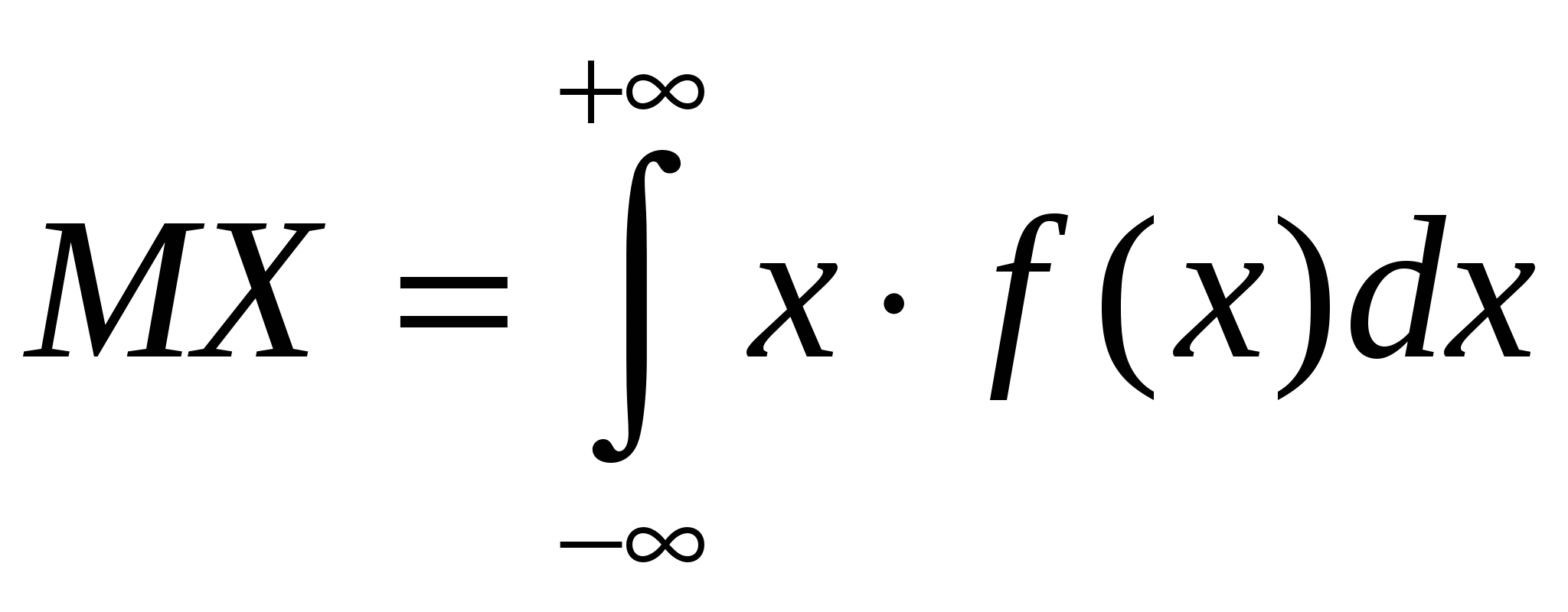 ,
,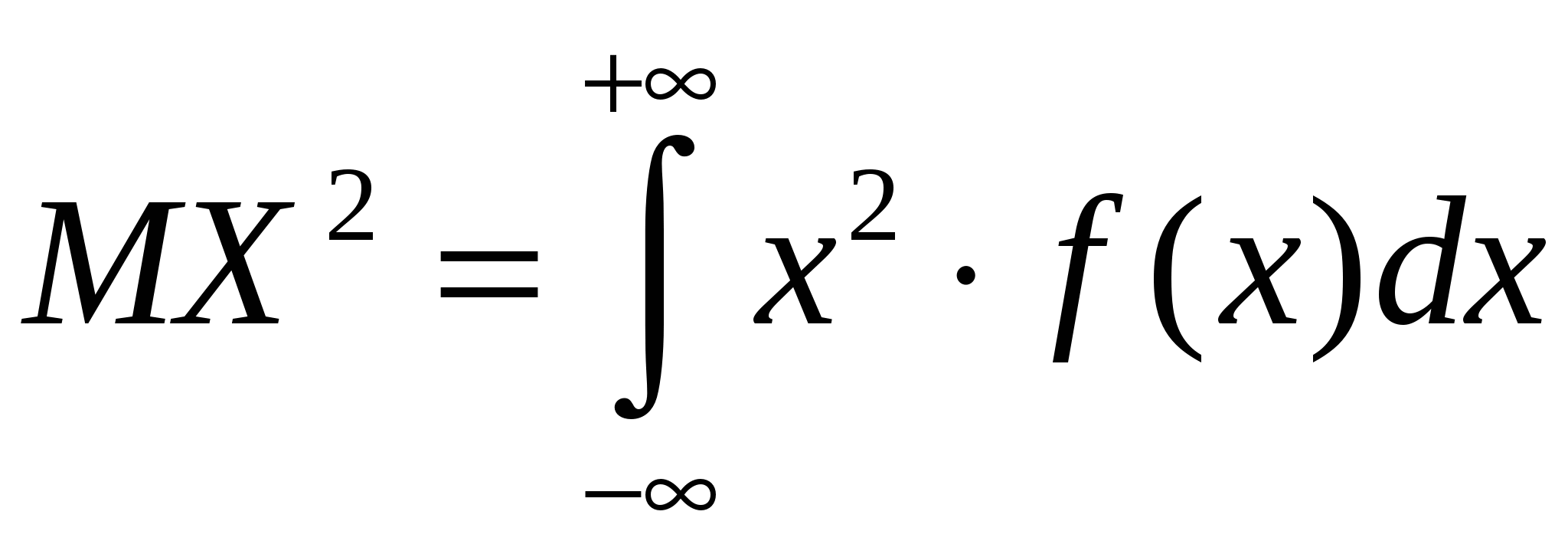
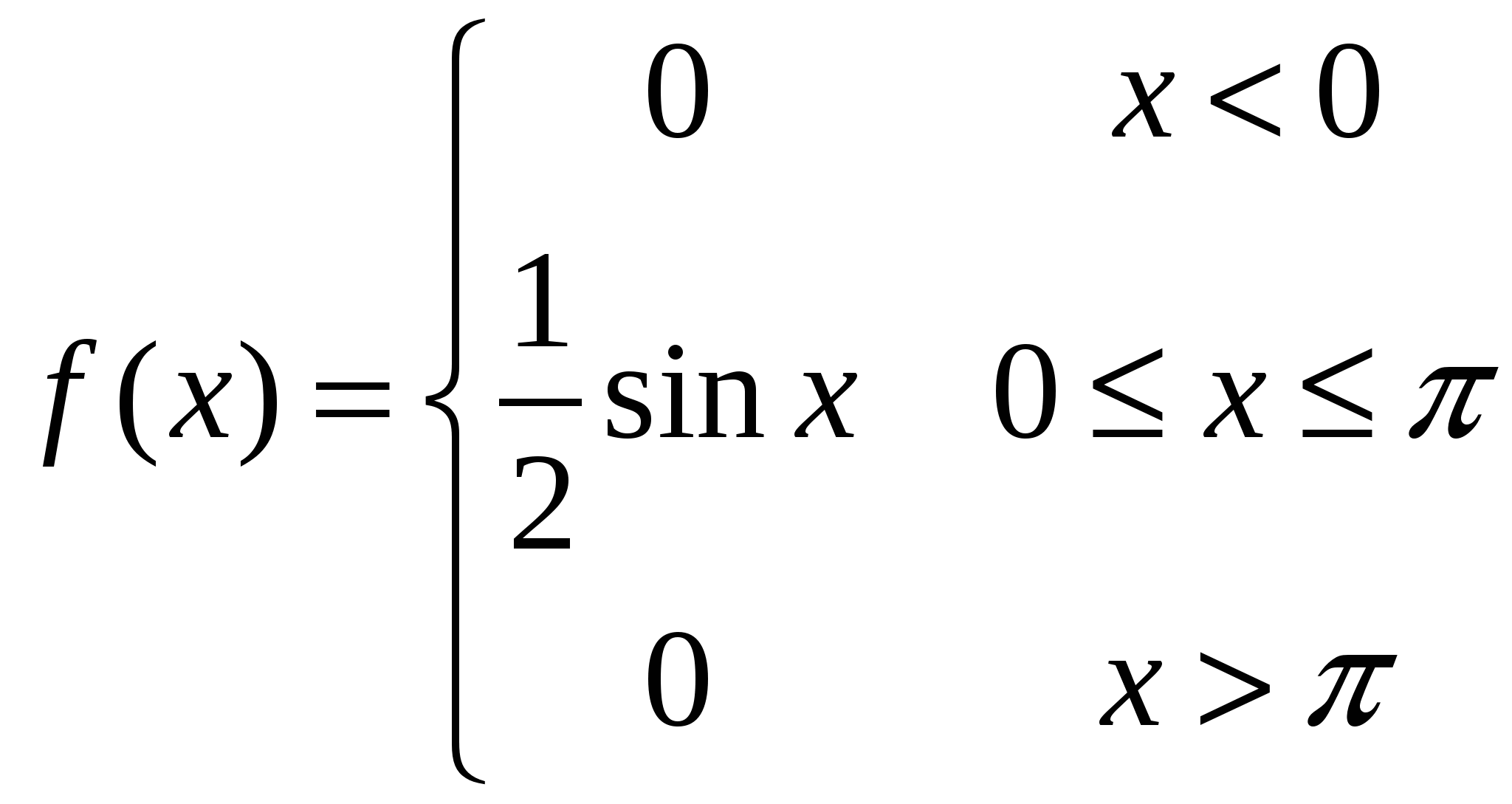
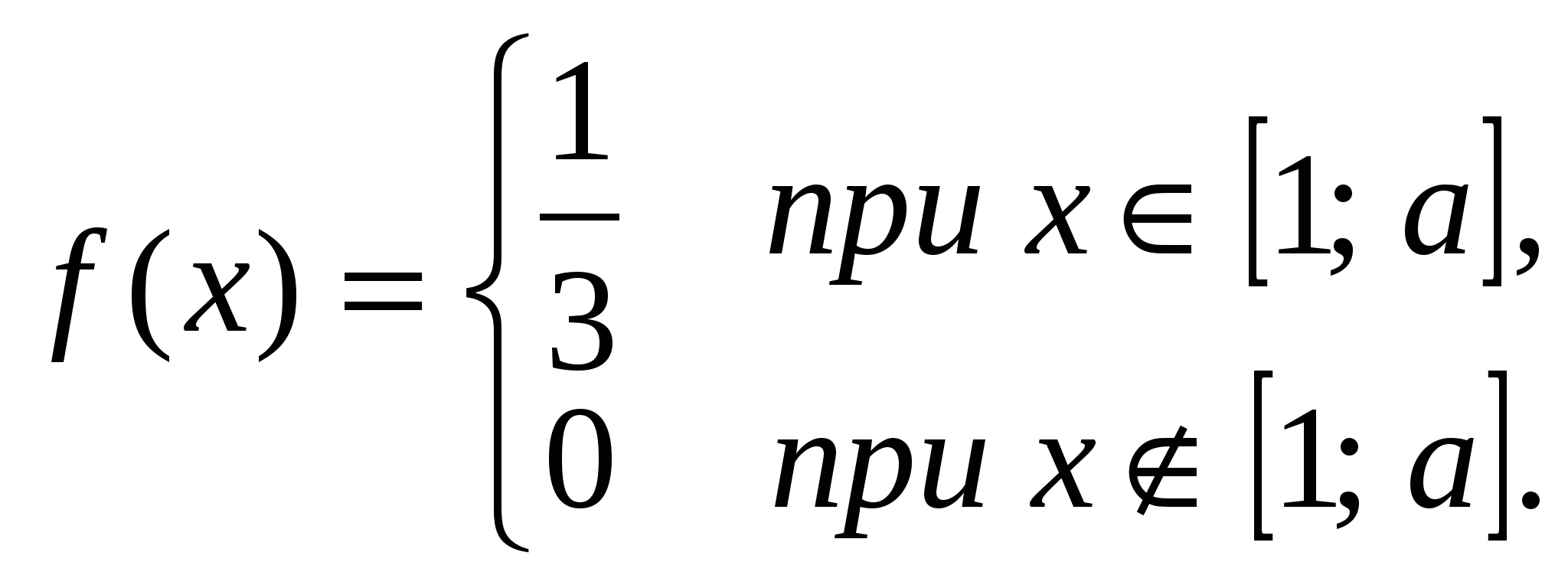
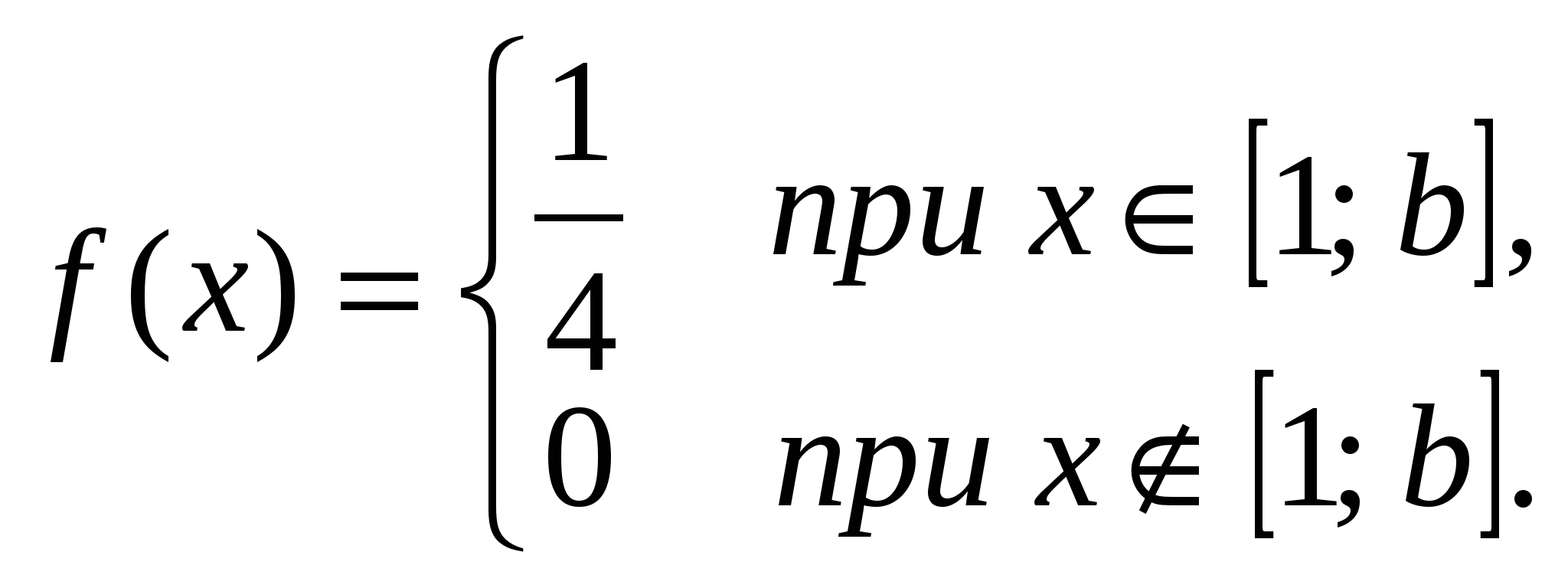
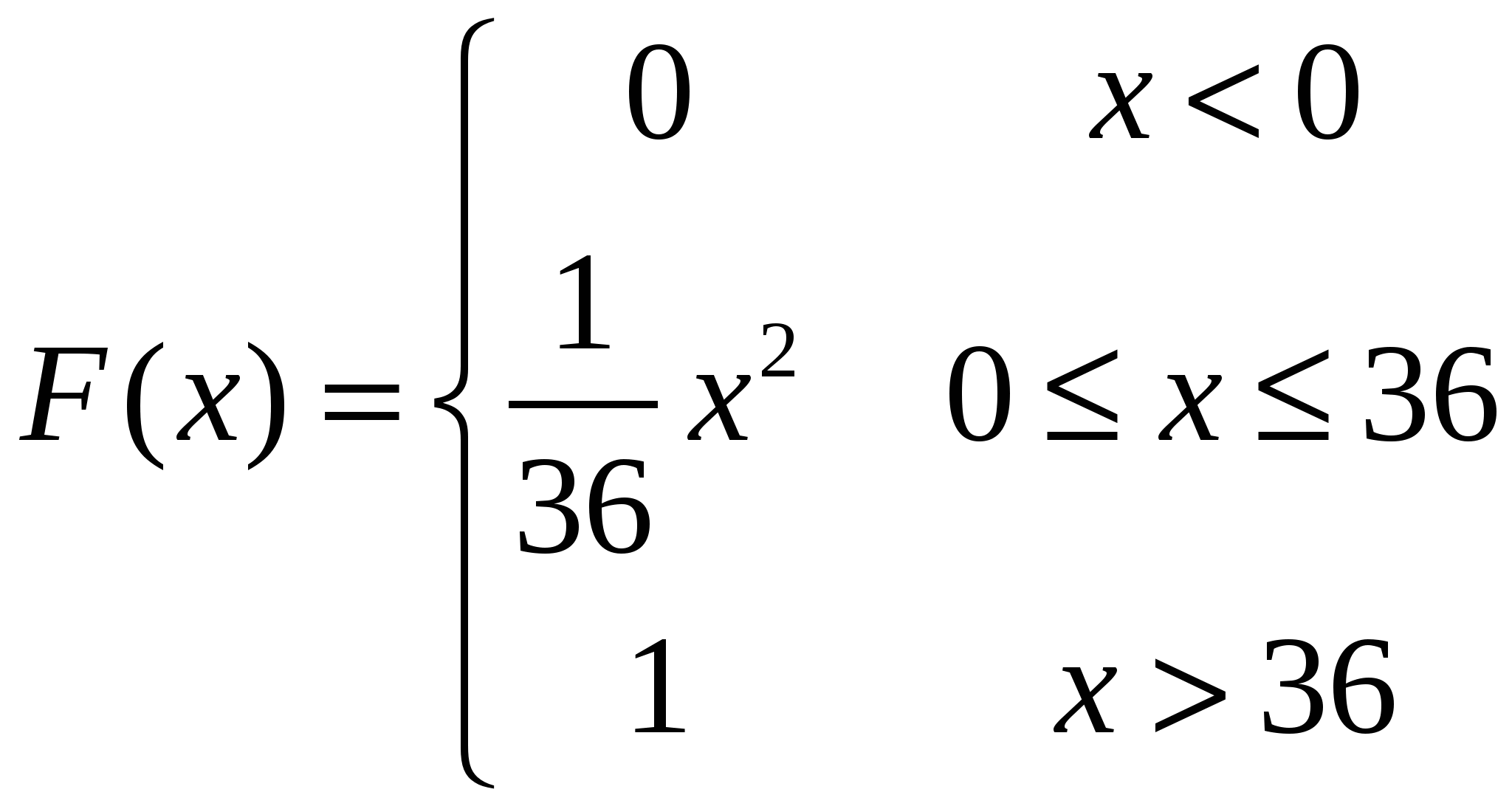
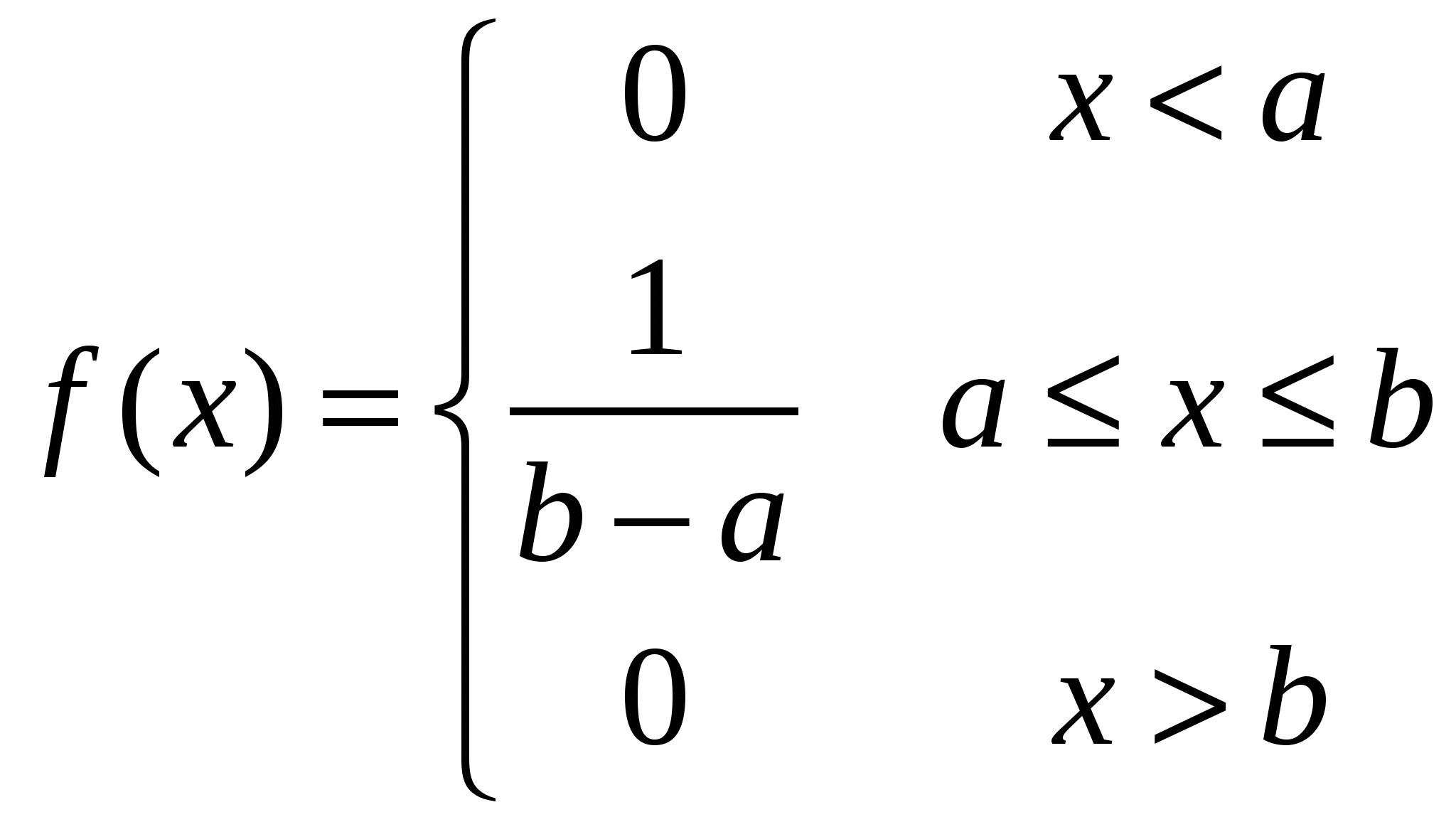
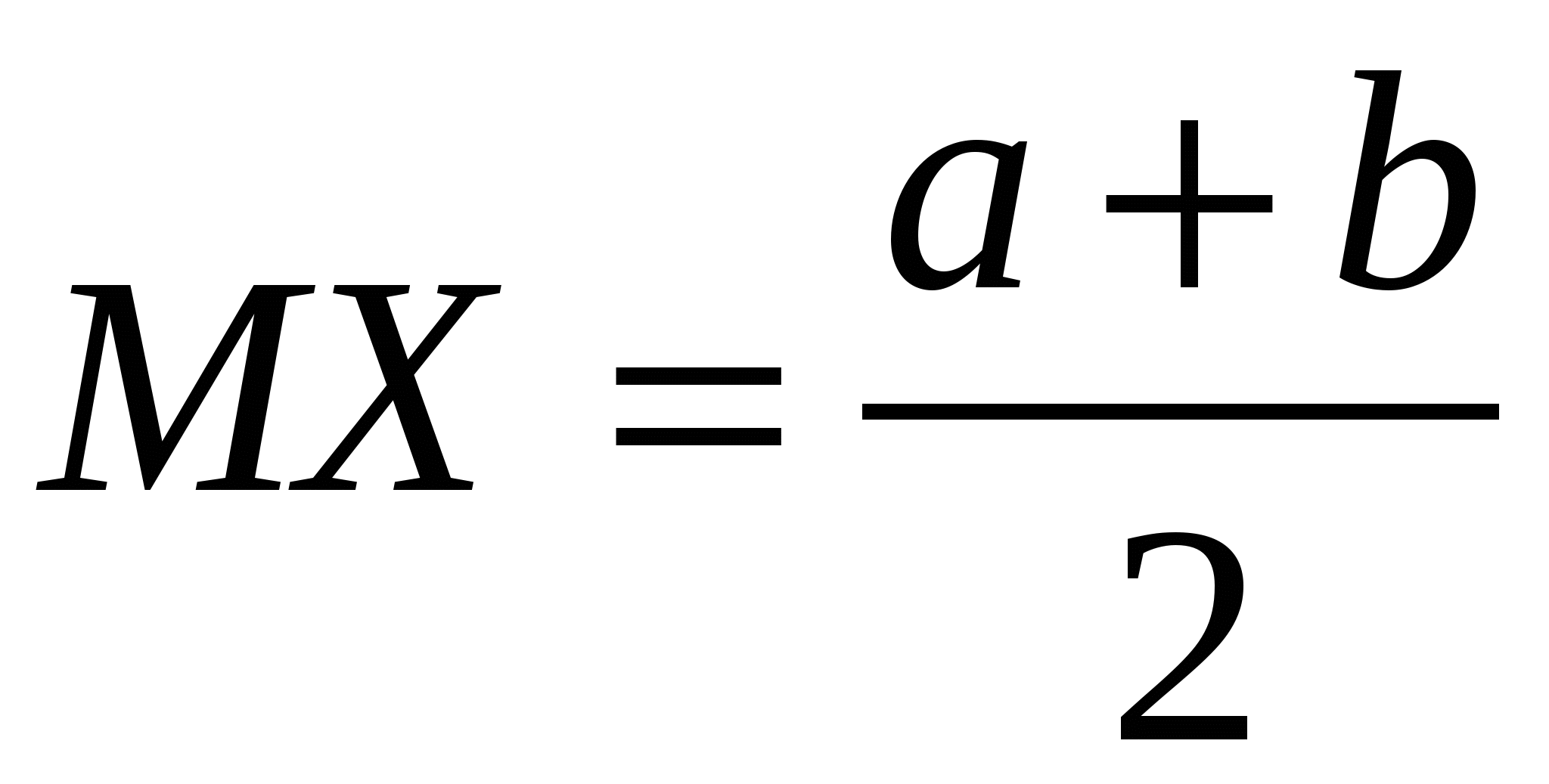 ,
, 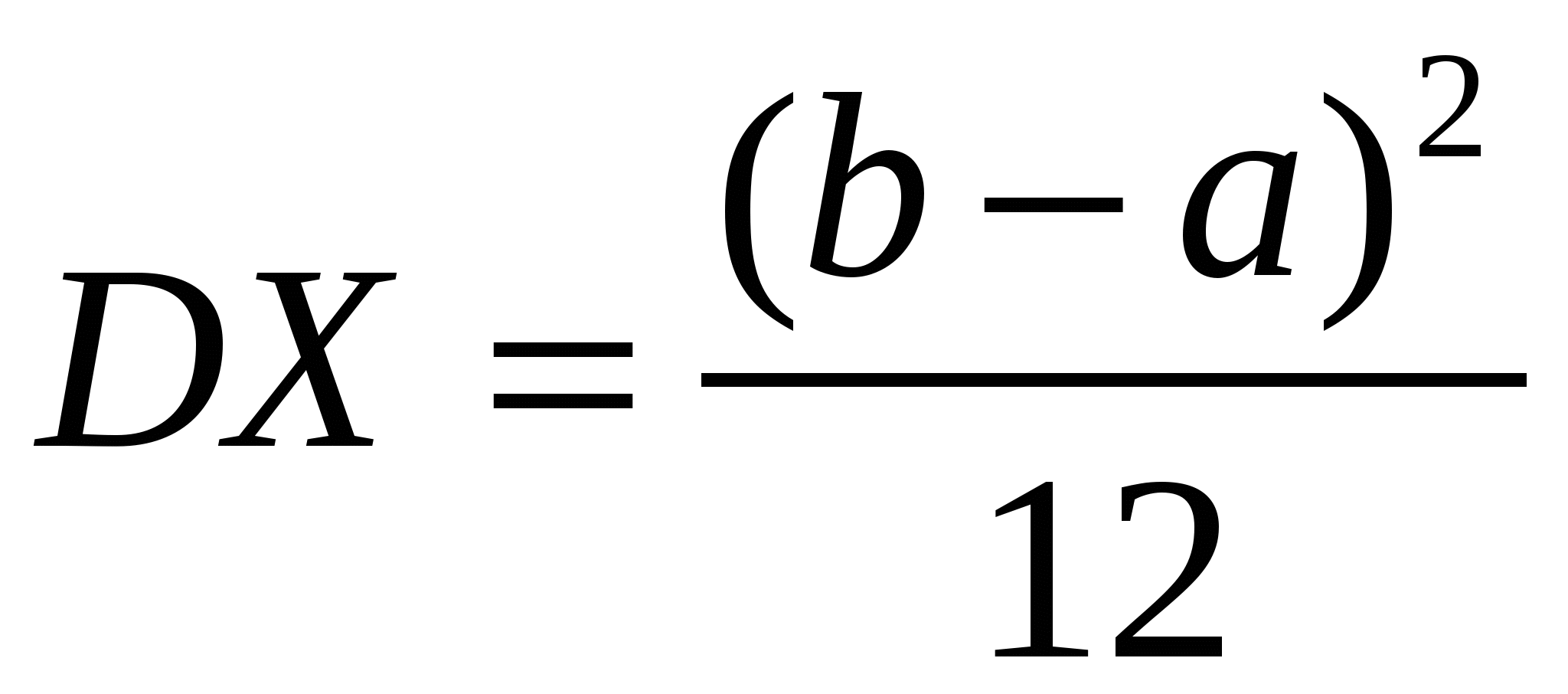
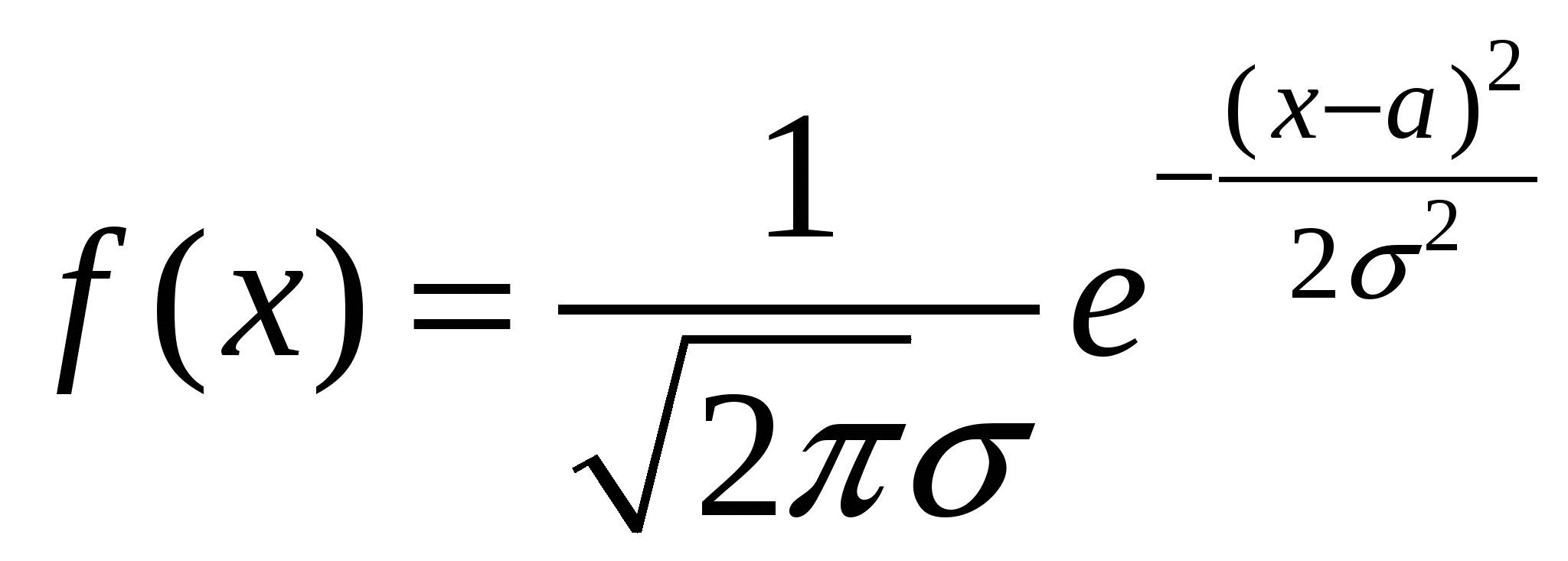
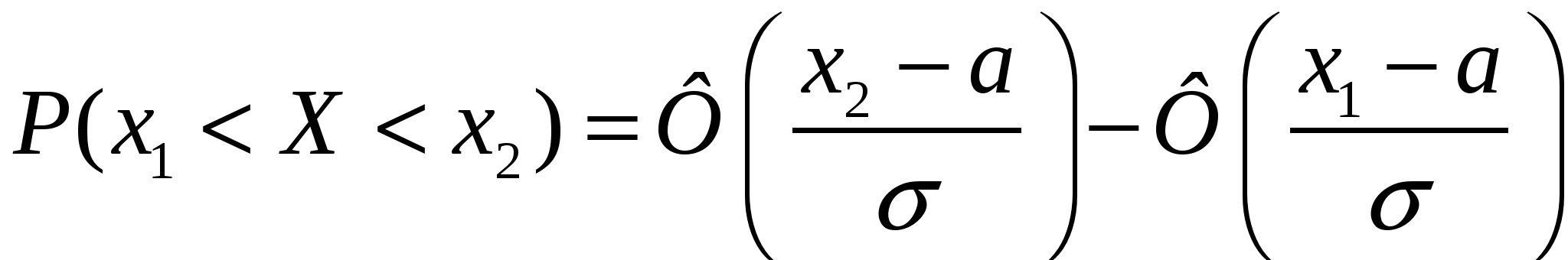 , где Ф(x)=
, где Ф(x)= 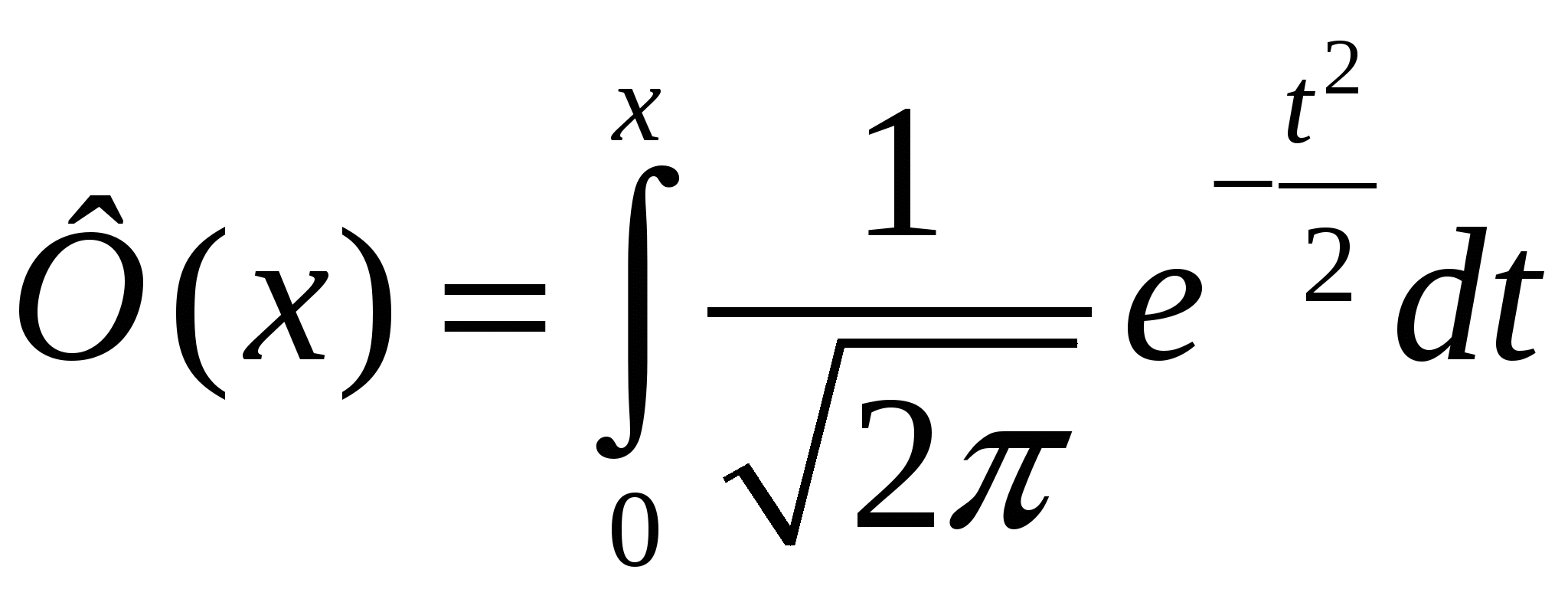 — функция Лапласа.
— функция Лапласа.